Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-19T04:05:23.860Z Has data issue: false hasContentIssue false
  • English
  • Français

Coefficients of ergodicity for stochastically monotone Markov chains

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

G. Ch. Pflug  and
W. Schachermayer
G. Ch. Pflug*
Affiliation:
University of Vienna
W. Schachermayer*
Affiliation:
University of Vienna
*
∗ Postal address: Universität Wien, Institut für Statistik und Informatik, Universitätstrasse 5/9, A-1010 Wien, Austria.
∗ Postal address: Universität Wien, Institut für Statistik und Informatik, Universitätstrasse 5/9, A-1010 Wien, Austria.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we show that to each distance d defined on the finite state space S of a strongly ergodic Markov chain there corresponds a coefficient ρd of ergodicity based on the Wasserstein metric. For a class of stochastically monotone transition matrices P, the infimum over all such coefficients is given by the spectral radius of P – R, where R = limkPk and is attained. This result has a probabilistic interpretation of a control of the speed of convergence of 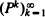by the metric d and is linked to the second eigenvalue of P.

Keywords

ERGODIC COEFFICIENTSWASSERSTEIN METRICBIRTH AND DEATH MATRIX

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Papers
Information
Journal of Applied Probability , Volume 29 , Issue 4 , December 1992 , pp. 850 - 860
Copyright
Copyright © Applied Probability Trust 1992 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Daley, D. J. (1968) Stochastically monotone Markov chains. Z. Wahrscheinlichkeitsth. 10, 305–317.Google Scholar
[2] Dobrushin, R. L. (1956) Central limit theorems for non-stationary Markov chains I. Theory Prob. Appl. 1, 65–80.Google Scholar
[3] Dudley, R. M. (1976) Probability and Metrics. Aarhus University Lecture Notes 45, 1–126.Google Scholar
[4] Isaacson, D. and Luecke, G. R. (1978) Strongly ergodic Markov chains and rates of convergence using spectral conditions. Stoch. Proc. Appl. 7, 113–121.Google Scholar
[5] Isaacson, D. and Madsen, R. (1976) Markov Chains. Wiley, New York.Google Scholar
[6] Karlin, S. (1966) A First Course in Stochastic Processes. Academic Press, New York.Google Scholar
[7] Kemeny, J. G. and Snell, J. L. (1976) Finite Markov Chains. Springer-Verlag, New York.Google Scholar
[8] Nummelin, E. and Tweedie, R. L. (1978) Geometric ergodicity and R-positivity for general Markov chains. Ann. Prob. 6, 404–420.CrossRefGoogle Scholar
[9] Rachev, S. T. (1984) The Monge-Kantorovich mass transformance problem and its stochastic applications. Theory Prob. Appl. 29, 647–676.CrossRefGoogle Scholar
[10] Seneta, E. (1981) Non-negative Matrices and Markov Chains, 2nd edn. Springer-Verlag, Berlin.Google Scholar
[11] Vallender, S. S. (1973) Calculation of the Wasserstein-distance between probability distributions on the line. Theory Prob. Appl. 18, 784–786.Google Scholar