Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-16T15:14:40.754Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of random variables with stationary digits

Part of: Stochastic processes

Published online by Cambridge University Press:  15 August 2022

Horia D. Cornean Open the ORCID record for Horia D. Cornean [Opens in a new window] ,
Ira W. Herbst ,
Jesper Møller Open the ORCID record for Jesper Møller [Opens in a new window] ,
Kasper S. Sørensen  and
Benjamin B. Støttrup Open the ORCID record for Benjamin B. Støttrup [Opens in a new window]
Horia D. Cornean*
Affiliation:
Aalborg University
Ira W. Herbst*
Affiliation:
University of Virginia
Jesper Møller*
Affiliation:
Aalborg University
Kasper S. Sørensen*
Affiliation:
Aalborg University
Benjamin B. Støttrup*
Affiliation:
Aalborg University
*
*Postal address: Department of Mathematical Sciences, Aalborg University, Skjernvej 4A, 9220 Aalborg, Denmark
**Postal address: Department of Mathematics, University of Virginia, Charlottesville, VA 22903, USA
*Postal address: Department of Mathematical Sciences, Aalborg University, Skjernvej 4A, 9220 Aalborg, Denmark
*Postal address: Department of Mathematical Sciences, Aalborg University, Skjernvej 4A, 9220 Aalborg, Denmark
*Postal address: Department of Mathematical Sciences, Aalborg University, Skjernvej 4A, 9220 Aalborg, Denmark
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 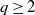$q\ge2$ be an integer, 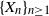$\{X_n\}_{n\geq 1}$ a stochastic process with state space 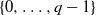$\{0,\ldots,q-1\}$ , and F the cumulative distribution function (CDF) of 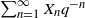$\sum_{n=1}^\infty X_n q^{-n}$ . We show that stationarity of 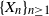$\{X_n\}_{n\geq 1}$ is equivalent to a functional equation obeyed by F, and use this to characterize the characteristic function of X and the structure of F in terms of its Lebesgue decomposition. More precisely, while the absolutely continuous component of F can only be the uniform distribution on the unit interval, its discrete component can only be a countable convex combination of certain explicitly computable CDFs for probability distributions with finite support. We also show that 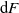$\mathrm{d} F$ is a Rajchman measure if and only if F is the uniform CDF on [0, 1].

Keywords

Functional equationLebesgue decompositionMinkowski’s question-mark functionmixture distributionRajchman measuresingular function

MSC classification

Primary: 60G10: Stationary processes
Secondary: 60G30: Continuity and singularity of induced measures
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 931 - 947
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbaroux, J.-M., Combes, J.-M. and Montcho, R. (1997). Remarks on the relation between quantum dynamics and fractal spectra. J. Math. Anal. Appl. 213, 698–722.CrossRefGoogle Scholar
Billingsley, P. (1965). Ergodic Theory and Information. Wiley, Chichester.Google Scholar
Billingsley, P. (1995). Probability and Measure. Wiley Series in Probability and Statistics. Wiley, Chichester.Google Scholar
Denjoy, A. (1932). Sur quelques points de la théorie des fonctions. C. R. Math. Acad. Sci. Paris 194, 44–46.Google Scholar
Denjoy, A. (1934). Sur une fonction de Minkowski. C. R. Math. Acad. Sci. Paris 198, 44–47.Google Scholar
Dym, H. (1968). On a class of monotone functions generated by ergodic sequences. Amer. Math. Monthly 75, 594–601.CrossRefGoogle Scholar
Folland, G. B. (1999). Real Analysis, Modern Techniques and Their Applications, 2nd edn. Wiley, Chichester.Google Scholar
Harris, T. E. (1955). On chains of infinite order. Pacific J. Math. 5, 707–724.CrossRefGoogle Scholar
Hu, T.-Y. (2001). Asymptotic behavior of Fourier transforms of self-similar measures. Proc. Amer. Math. Soc. 129, 1713–1720.CrossRefGoogle Scholar
Hutchinson, J. E. (1981). Fractals and self similarity. Indiana Univ. Math. J. 30, 713–747.CrossRefGoogle Scholar
Jordan, T. and Sahlsten, T. (2016). Fourier transforms of Gibbs measures for the Gauss map. Math. Ann. 364, 983–1023.CrossRefGoogle Scholar
Kairies, H. (1997). Functional equations for peculiar functions. Aequationes Math. 53, 207–241.CrossRefGoogle Scholar
Lyons, R. (1995). Seventy years of Rajchman measures. In The Journal of Fourier Analysis and Applications, ed. J. J. Benedetto, CRC Press, Boca Raton, FL, pp. 363–377.Google Scholar
Minkowski, H. (1904). Zur Geometrie der Zahlen, Verhandlungen des III. Internationalen Mathematiker-Kongresses in Heidelberg, 1904, pp. 164–173. (Gesammelte Abhandlungen von Hermann Minkowski. Bd. II. B. G. Teubner, Leipzig, 1911, pp. 43–52). Reprinted by Chelsea, New York, 1967.Google Scholar
Parry, W. (1960). On the $\beta$ -expansion of real numbers. Acta Math. Hung. 11, 401–416.CrossRefGoogle Scholar
Peres, Y., Schlag, W. and Solomyak, B. (2000). Sixty years of Bernoulli convolutions. In Fractal Geometry and Stochastics II, eds C. Brandt, S. Graf, and M. Zähle, Birkhäuser, Basel, pp. 39–65.CrossRefGoogle Scholar
Persson, T. (2015). On a problem by R. Salem concerning Minkowski’s question mark function. Preprint, arXiv:1501.00876.Google Scholar
Reese, S. (1989). Some Fourier–Stieltjes coefficients revisited. Proc. Amer. Math. Soc. 105, 384–386.CrossRefGoogle Scholar
Riesz, F. (1909). Sur les opérations fonctionnelles linéaires. C. R. Acad. Sci. Paris 149, 974–977.Google Scholar
Riesz, F. and Sz.-Nagy, B. (1955). Functional Analysis. Dover Publications, Mineola, NY.Google Scholar
Rudin, W. (1976). Principles of Mathematical Analysis . International Series in Pure and Applied Mathematics. McGraw-Hill, New York.Google Scholar
Salem, R. (1943). Some singular monotonic functions which are strictly increasing. Trans. Amer. Math. Soc. 53, 427–439.CrossRefGoogle Scholar
Strichartz, R. S. (1990). Self-similar measures and their Fourier transforms, I. Indiana Univ. Math. J. 39, 797–817.CrossRefGoogle Scholar
Takács, L. (1978). An increasing continuous singular function. Amer. Math. Monthly 85, 35–37.CrossRefGoogle Scholar
Varjú, P. P. (2018). Recent progress on Bernoulli convolutions. In Proc. Seventh European Congress of Mathematics, eds V. Mehrmann and M. Skutella. American Mathematical Society, Providence, RI, pp. 847–867.CrossRefGoogle Scholar