Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T13:30:46.115Z Has data issue: false hasContentIssue false
  • English
  • Français

The characterization of distributions by order statistics and record values — a unified approach

Published online by Cambridge University Press:  14 July 2016

Paul Deheuvels
Paul Deheuvels*
Affiliation:
Université Paris VI and Ecole Pratique des Hautes Etudes
*
∗ Postal address: 7 Avenue du Château, 92340 Bourg-la-Reine, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

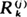It is shown that, in some particular cases, it is equivalent to characterize a continuous distribution by properties of records and by properties of order statistics. As an application, we give a simple proof that if two successive jth record values and 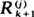associated to an i.i.d. sequence are such that 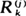and 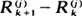are independent, then the sequence has to derive from an exponential distribution (in the continuous case). The equivalence breaks up for discrete distributions, for which we give a proof that the only distributions such that Xk, n and Xk+1, n – Xk, n are independent for some k ≧ 2 (where Xk, n is the kth order statistic of X1, ···, Xn) are degenerate.

Keywords

CHARACTERIZATION THEOREMSEXPONENTIAL AND GEOMETRIC DISTRIBUTIONSRECORDS
Type
Research Papers
Information
Journal of Applied Probability , Volume 21 , Issue 2 , June 1984 , pp. 326 - 334
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ahsanullah, M. (1978) Record values and the exponential distribution. Ann. Inst. Statist. Math. 30, 429–433.Google Scholar
[2] Ahsanullah, M. (1979) Characterization of the exponential distribution by record values. Sankya 41 B, 116–121.Google Scholar
[3] Ahsanullah, M. (1981) Record values of exponentially distributed random variables. Statist. Hefte 22 (2), 121–127.Google Scholar
[4] Arnold, B. C., Becker, A., Gather, H. and Zahedi, H. (1983) On the Markov-property of order statistics. J. Statist. Planning Inference. To appear.Google Scholar
[5] Chandler, K. N. (1952) The distribution and frequency of record values. J. R. Statist. Soc. B 14, 220–228.Google Scholar
[6] Crawford, C. B. (1966) Characterization of geometric and exponential distributions. Ann. Math. Statist. 37, 1790–1795.CrossRefGoogle Scholar
[7] Dallas, A. C. (1981) Record values and the exponential distribution. J. Appl. Prob. 18, 949–951.Google Scholar
[8] David, H. A. (1981) Order Statistics, 2nd. edn. Wiley, New York.Google Scholar
[9] Deheuvels, P. (1983) The strong approximation of extremal processes (II). Z. Wahrscheinlichkeitsth 62, 7–15.Google Scholar
[10] Dziubdziela, W. and Kopocinski, B. (1976) Limiting properties of the kth record values. Applicationes Math. 15, 187–190.Google Scholar
[11] Ferguson, T. S. (1964) A characterization of the exponential distribution. Ann. Math. Statist. 35, 1199–1207.Google Scholar
[12] Ferguson, T. S. (1965) A characterization of the geometric distribution. Amer. Math. Monthly 72, 256–260.Google Scholar
[13] Fisz, M. (1958) Characterization of probability distributions. Skand. Aktuarietiskr. 1–2, 65–70.Google Scholar
[14] Galambos, J. (1972) Characterization of certain populations by independence of order statistics. J. Appl. Prob. 9, 224–230.CrossRefGoogle Scholar
[15] Galambos, J. (1975) Characterization of probability distributions by properties of order statistics, I and II. In Statistical Distributions in Scientific Work 3, ed. Patil, G. P., Kotz, S. and Ord, J. K., Riedel, Dordrecht, 89–101.Google Scholar
[16] Galambos, J. (1978) The Asymptotic Theory of Extreme Order Statistics. Wiley, New York.Google Scholar
[17] Gupta, R. C. (1983) Relationships between order statistics and record values and some characterization results. J. Appl. Prob. 21, 433–438.Google Scholar
[18] Galambos, J. and Kotz, S. (1977) Characterizations of Probability Distributions. Lecture Notes in Mathematics 675, Springer-Verlag, Berlin.Google Scholar
[19] Kemperman, J. H. B. (1971) Product measures for which deviation and minimum are independent. Sankhya A 33, 271–288.Google Scholar
[20] Pfeifer, D. (1979) ‘Record values’ in einem stochastischen modell mit nicht-identischen verteilungen. , Aachen.Google Scholar
[21] Pfeifer, D. (1982) Characterizations of exponential distributions by independent non-stationary record increments. J. Appl. Prob. 19, 127–135.CrossRefGoogle Scholar
[22] Rossberg, H. J. (1960) Über die verteilungsfunktionen der differenzen und quotienten von ranggrössen. Math. Nachr. 21, 27–39.Google Scholar
[23] Rossberg, H. J. (1972) Characterization of distribution functions by the independence of certain functions of order statistics. Sankhya A 34, 111–120.Google Scholar
[24] Srivastava, R. C. (1978) Some characterizations of the exponential distribution based on record values. Ohio State University, Tech. Report 170.Google Scholar
[25] Srivastava, R. C. (1981) Some characterizations of the exponential distribution based on record values, In: Statistical Distributions in Scientific Work 4, ed. Taillie, C., Patil, G. P. and Baldessari, B., Reidel, Dordrecht, 417–418.Google Scholar
[26] Sukhatme, P. V. (1937) Tests of significance for samples of the χ 2 population with two degrees of freedom. Ann. Eugenics 8, 52–56.Google Scholar
[27] Taillie, C. (1981) A note on Srivastava's characterization of the exponential distribution based on record values, In: Statistical Distributions in Scientific Work, 4, ed. Taillie, C., Patil, G. P. and Baldessari, B., Reidel, Dordrecht, 417–418.Google Scholar
[28] Tata, M. N. (1969) On outstanding values in a sequence of random variables. Z. Wahrscheinlichkeitsth. 12, 9–20.Google Scholar