Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Diaconis, Persi
and
Freedman, David
1999.
Iterated Random Functions.
SIAM Review,
Vol. 41,
Issue. 1,
p.
45.
Wu, Wei Biao
and
Woodroofe, Michael
2000.
A central limit theorem for iterated random functions.
Journal of Applied Probability,
Vol. 37,
Issue. 3,
p.
748.
Wu, Wei Biao
and
Woodroofe, Michael
2000.
A central limit theorem for iterated random functions.
Journal of Applied Probability,
Vol. 37,
Issue. 03,
p.
748.
Lee, Oe-Sook
2003.
A STUDY ON GARCH(p, q) PROCESS.
Communications of the Korean Mathematical Society,
Vol. 18,
Issue. 3,
p.
541.
Brofferio, Sara
2003.
Speed of stochastic locally contractive systems.
The Annals of Probability,
Vol. 31,
Issue. 4,
Hennion, Hubert
and
Hervé, Loïc
2004.
Central limit theorems for iterated random Lipschitz mappings.
The Annals of Probability,
Vol. 32,
Issue. 3,
Lagerås, Andreas Nordvall
and
Stenflo, Örjan
2005.
Central limit theorems for contractive Markov chains.
Nonlinearity,
Vol. 18,
Issue. 5,
p.
1955.
Buraczewski, Dariusz
2007.
On invariant measures of stochastic recursions in a critical case.
The Annals of Applied Probability,
Vol. 17,
Issue. 4,
Hervé, Loïc
2008.
Vitesse de convergence dans le théorème limite central pour des chaînes de Markov fortement ergodiques.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 44,
Issue. 2,
Mirek, Mariusz
2011.
Heavy tail phenomenon and convergence to stable laws for iterated Lipschitz maps.
Probability Theory and Related Fields,
Vol. 151,
Issue. 3-4,
p.
705.
Buraczewski, Dariusz
Damek, Ewa
and
Mirek, Mariusz
2012.
Asymptotics of stationary solutions of multivariate stochastic recursions with heavy tailed inputs and related limit theorems.
Stochastic Processes and their Applications,
Vol. 122,
Issue. 1,
p.
42.
Damek, Ewa
Mentemeier, Sebastian
Mirek, Mariusz
and
Zienkiewicz, Jacek
2013.
Convergence to Stable Laws for Multidimensional Stochastic Recursions: The Case of Regular Matrices.
Potential Analysis,
Vol. 38,
Issue. 3,
p.
683.
Guibourg, Denis
and
Hervé, Loïc
2013.
Multidimensional Renewal Theory in the Non-Centered Case. Application to Strongly Ergodic Markov Chains.
Potential Analysis,
Vol. 38,
Issue. 2,
p.
471.
Hervé, Loïc
and
Pène, Françoise
2013.
On the Recurrence Set of Planar Markov Random Walks.
Journal of Theoretical Probability,
Vol. 26,
Issue. 1,
p.
169.
Hervé, Loïc
and
Ledoux, James
2023.
Robustness of iterated function systems of Lipschitz maps.
Journal of Applied Probability,
Vol. 60,
Issue. 3,
p.
921.
Alsmeyer, Gerold
and
Mukherjee, Chiranjib
2023.
On Null-Homology and Stationary Sequences.
Journal of Theoretical Probability,
Vol. 36,
Issue. 4,
p.
2476.
Pène, Françoise
2024.
Probabilistic limit theorems via the operator perturbation method, under optimal moment assumptions.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 60,
Issue. 3,
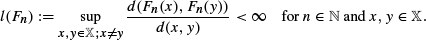 Conditions on the distribution of l(Fn) are given for the existence of an invariant distribution of X0 making the process (Xn)n≥0 stationary and ergodic. Our main result corrects a central limit theorem by Łoskot and Rudnicki (1995) and removes an error in its proof. Instead of trying to compare the sequence φ (Xn)n≥0 for some φ : 𝕏 → ℝ with a triangular scheme of independent random variables our proof is based on an approximation by a martingale difference scheme.
Conditions on the distribution of l(Fn) are given for the existence of an invariant distribution of X0 making the process (Xn)n≥0 stationary and ergodic. Our main result corrects a central limit theorem by Łoskot and Rudnicki (1995) and removes an error in its proof. Instead of trying to compare the sequence φ (Xn)n≥0 for some φ : 𝕏 → ℝ with a triangular scheme of independent random variables our proof is based on an approximation by a martingale difference scheme.

