Published online by Cambridge University Press: 13 March 2023
The Bruss–Robertson–Steele (BRS) inequality bounds the expected number of items of random size which can be packed into a given suitcase. Remarkably, no independence assumptions are needed on the random sizes, which points to a simple explanation; the inequality is the integrated form of an  $\omega$-by-
$\omega$-by-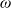 $\omega$ inequality, as this note proves.
$\omega$ inequality, as this note proves.