Hostname: page-component-6587cd75c8-ptrpl Total loading time: 0 Render date: 2025-04-23T20:13:29.464Z Has data issue: false hasContentIssue false
  • English
  • Français

Boolean percolation on digraphs and random exchange processes

Part of: Markov processes Equilibrium statistical mechanics

Published online by Cambridge University Press:  25 October 2023

Georg Braun
Georg Braun*
Affiliation:
Eberhard Karls Universität Tübingen
*
*Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study in a general graph-theoretic formulation a long-range percolation model introduced by Lamperti [27]. For various underlying digraphs, we discuss connections between this model and random exchange processes. We clarify, for all $n \in \mathbb{N}$, under which conditions the lattices $\mathbb{N}_0^n$ and $\mathbb{Z}^n$ are essentially covered in this model. Moreover, for all 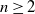$n \geq 2$, we establish that it is impossible to cover the directed n-ary tree in our model.

Keywords

Rumour spread and firework processinfinite paths in random graphslong-range percolationinfinite-type branching process

MSC classification

Primary: 82B43: Percolation
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 3 , September 2024 , pp. 755 - 766
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlberg, D., Broman, E. I., Griffiths, S. and Morris, R. (2014). Noise sensitivity in continuum percolation. Israel J. Math. 201, 847–899.10.1007/s11856-014-1038-yCrossRefGoogle Scholar
Ahlberg, D., Tassion, V. and Teixeira, A. Q. (2018). Sharpness of the phase transition for continuum percolation in $\mathbb {R}^ 2$ . Prob. Theory Relat. Fields 172, 525–581.10.1007/s00440-017-0815-8CrossRefGoogle Scholar
Athreya, S. R., Roy, R. and Sarkar, A. (2004). On the coverage of space by random sets. Adv. Appl. Prob. 36, 1–18.10.1239/aap/1077134461CrossRefGoogle Scholar
Benkherouf, L. and Bather, J. A. (1988). Oil exploration: sequential decisions in the face of uncertainty. J. Appl. Prob. 25, 529–543.10.2307/3213982CrossRefGoogle Scholar
Bertacchi, D. and Zucca, F. (2009). Characterization of critical values of branching random walks on weighted graphs through infinite-type branching processes. J. Statist. Phys. 134, 53–65.10.1007/s10955-008-9653-5CrossRefGoogle Scholar
Bertacchi, D. and Zucca, F. (2013). Rumor processes in random environment on $\mathbb{N}$ and on Galton–Watson trees. J. Statist. Phys. 153, 486–511.10.1007/s10955-013-0843-4CrossRefGoogle Scholar
Bezborodov, V. (2021). Non-triviality in a totally asymmetric one-dimensional Boolean percolation model on a half-line. Statist. Prob. Lett. 176, 109155.10.1016/j.spl.2021.109155CrossRefGoogle Scholar
Bezborodov, V. and Krueger, T. (2023). Linear and superlinear spread for continuous-time frog model. Available at arXiv:2008.10585.Google Scholar
Braunsteins, P. T. (2018). Extinction in branching processes with countably many types. Doctoral thesis, University of Melbourne. Available at https://minerva-access.unimelb.edu.au/handle/11343/210538.Google Scholar
Braunsteins, P. T. and Haupthenne, S. (2019). Extinction in lower Hessenberg processes with countably many types. Ann. Appl. Prob. 29, 2782–2818.10.1214/19-AAP1464CrossRefGoogle Scholar
Coletti, C. F. and Grynberg, S. P. (2014). Absence of percolation in the Bernoulli Boolean model. Available at arXiv:1402.3118.Google Scholar
Coletti, C. F., Miranda, D. and Grynberg, S. P. (2020). Boolean percolation on doubling graphs. J. Statist. Phys. 178, 814–831.10.1007/s10955-019-02462-6CrossRefGoogle Scholar
Duminil-Copin, H., Raoufi, A. Tassion, V. (2020). Subcritical phase of d-dimensional Poisson–Boolean percolation and its vacant set. Ann. H. Lebesgue 3, 677–700.10.5802/ahl.43CrossRefGoogle Scholar
Gade, H. G. (1973). Deep water exchanges in a sill fjord: a stochastic process. J. Phys. Oceanogr. 3, 213–219.10.1175/1520-0485(1973)003<0213:DWEIAS>2.0.CO;22.0.CO;2>CrossRefGoogle Scholar
Gallo, S., Garcia, N. L., Junior, V. V. and Rodrguez, P. M. (2014). Rumor processes on $\mathbb{N}$ and discrete renewal processes. J. Statist. Phys. 155, 591–602.10.1007/s10955-014-0959-1CrossRefGoogle Scholar
Gantert, N. and Müller, S. (2006). The critical Markov chain is transient. Markov Process. Relat. Fields 12, 805–814.Google Scholar
Gilbert, E. N. (1961). Random plane networks. J. Soc. Indust. Appl. Math. 9, 533–543.10.1137/0109045CrossRefGoogle Scholar
Gouéré, J.-B. (2008). Subcritical regimes in the Poisson Boolean model of continuum percolation. Ann. Prob. 36, 1209–1220.10.1214/07-AOP352CrossRefGoogle Scholar
Hall, P. (1988). Introduction to the Theory of Coverage Processes. John Wiley, New York.Google Scholar
Helland, I. S. (1974). A random exchange model with constant decrements. Report, University of Bergen. Available at https://bora.uib.no/bora-xmlui/handle/1956/19470.Google Scholar
Helland, I. S. and Nilsen, T. S. (1976). On a general random exchange model. J. Appl. Prob. 13, 781–790.10.2307/3212533CrossRefGoogle Scholar
Johnson, N. L., Kemp, A. W. and Kotz, S. (2005). Univariate Discrete Distributions. John Wiley, Hoboken, NJ.10.1002/0471715816CrossRefGoogle Scholar
Junior, V. V., Machado, F. P. and Ravishankar, K. (2019). The rumor percolation model and its variations. In Sojourns in Probability Theory and Statistical Physics II, ed. V. Sidoravicius, pp. 208–227. Springer, Singapore.Google Scholar
Junior, V. V, Machado, F. P. and Zuluaga, M. (2011). Rumor processes on $\mathbb{N}$ . J. Appl. Prob. 48, 624–636.10.1239/jap/1316796903CrossRefGoogle Scholar
Junior, V. V., Machado, F. P. and Zuluaga, M. (2014). The cone percolation on $\mathbb{T}_d$ . Brazilian J. Prob. Statist. 28, 367–375.10.1214/12-BJPS212CrossRefGoogle Scholar
Kellerer, H. G. (2006). Random dynamical systems on ordered topological spaces. Stoch. Dyn. 6, 255–300.10.1142/S0219493706001797CrossRefGoogle Scholar
Lamperti, J. W. (1970). Maximal branching processes and ‘long-range percolation’. J. Appl. Prob. 7, 89–98.10.2307/3212151CrossRefGoogle Scholar
Last, G., Penrose, M. D. and Zuyev, S. (2017). On the capacity functional of the infinite cluster of a Boolean model. Ann. Appl. Prob. 27, 1678–1701.10.1214/16-AAP1241CrossRefGoogle Scholar
Lebensztayn, É. and Rodríguez, P. M. (2008). The disk-percolation model on graphs. Statist. Prob. Lett. 78, 2130–2136.10.1016/j.spl.2008.02.001CrossRefGoogle Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation. Cambridge University Press, Cambridge.10.1017/CBO9780511895357CrossRefGoogle Scholar
Naor, P. (1957). Normal approximation to machine interference with many repairmen. J. R. Statist. Soc. B 19, 334–341.Google Scholar
Olver, F. W. J., Lozier, D. W., Boisvert, R. F. and Clark, C. W. (2010). NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge. Available in the form of a digital library at https://dlmf.nist.gov/.Google Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.10.1007/978-3-540-78859-1CrossRefGoogle Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1987). Stochastic Geometry and its Applications. John Wiley, Chichester.Google Scholar
Woess, W. (2000). Random Walks on Infinite Graphs and Groups. Cambridge University Press, Cambridge.10.1017/CBO9780511470967CrossRefGoogle Scholar
Zerner, M. P. W. (2018). Recurrence and transience of contractive autoregressive processes and related Markov chains. Electron. J. Prob. 23, 1–24.10.1214/18-EJP152CrossRefGoogle Scholar