Let R be a bounded open subset of N-dimensional Euclidean space EN,N ≧ 1, let {xt: t ≧ 0} be a separable Brownian motion starting at a point x ɛ R, and let τ = τR be the first time the motion hits the complement of R. It is known [1] that if g is a bounded measurable function on the boundary ∂R of R, then h(x) = Ex[g(xτ)] is a harmonic function of x ɛ R which “solves” the Dirichlet problem for the boundary function g; i.e., Δh = 0 on R, where Δ is the Laplacian. In elastic plate problems, one must solve the biharmonic equation 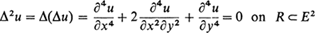subject to certain boundary conditions. For the more important applications, these boundary conditions involve the values of u and the normal derivative of u at points of ∂R. Even though a treatment of this Neumann type problem is not available at this time, some things can be said about biharmonic functions and their relationship to Brownian motion. We will show, in fact, that u(x)= Ex[τ(xτ)] is a biharmonic function on R which “satisfies” the boundary conditions (i) u=0 on ∂R and (ii) Δu= −2g on ∂R, provided g satisfies certain hypotheses. More generally, we will show that u(x)=Ex[Δkg(XΔ)] is polyharmonic of order k + 1 on R (i.e., Δk + 1u = Δ(Δku) = 0 on R) and that it satisfies certain boundary conditions. A treatment of the special case g ≡ 1 on ∂R can be found in [3].