Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T05:20:26.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Behavior of the supercritical phase of a continuum percolation model on ℝd

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

Hideki Tanemura
Hideki Tanemura*
Affiliation:
Chiba University
*
∗ Postal address: Department of Mathematics, Faculty of Science, Chiba University, Chiba 263, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

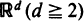A continuum percolation model on is considered. Using a renormalization technique developed by Grimmett and Marstrand, we show a continuum analogue of their results. We prove the critical value of the percolation equals the limit of the critical value of a slice as the thickness of the slice tends to infinity. We also prove that the effective conductivity in the model is bounded from below by a positive constant in the supercritical case.

Keywords

CRITICAL VALUEEFFECTIVE CONDUCTIVITYPOISSON BLOB MODELPOISSON DISTRIBUTIONRENORMALIZATION TECHNIQUE

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 2 , June 1993 , pp. 382 - 396
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Barlow, M. T. and Bass, R. F. (1990) On the resistance of the Sierpinski carpet. Proc. R. Soc. London A 431, 345–360.Google Scholar
[2] Bass, R. F. and Hsu, P. (1991) Some potential theory for reflecting Brownian motion in Holder and Lipschitz domains. Ann. Prob. 19, 486–508.CrossRefGoogle Scholar
[3] Chayes, J. T. and Chayes, L. (1986) Bulk transport properties and exponent inequalities for random resistor and flow networks. Comm. Math. Phys. 105, 133–152.CrossRefGoogle Scholar
[4] Doyle, P. G. and Snell, J. L. (1984) Random Walks and Electrical Networks. Mathematical Association of America, Washington, DC.CrossRefGoogle Scholar
[5] Fitzpatrick, J. P., Malt, R. B. and Spaepen, F. (1974) Percolation theory and the conductivity of random close packed mixtures of hard spheres. Phys. Lett. A 47, 207–208.CrossRefGoogle Scholar
[6] Grimmett, G. R. (1989) Percolation. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[7] Grimmett, G. R. and Kesten, H. (1984) First passage percolation, network flows and electrical resistances. Z. Wahrscheinlichkeitsth. 66, 335–366.CrossRefGoogle Scholar
[8] Grimmett, G. R. and Marstrand, J. M. (1990) The supercritical phase of percolation is well behaved. Proc. R. Soc. London A 430, 439–457.Google Scholar
[9] Hall, P. (1985) On continuum percolation. Ann. Prob. 13, 1250–1266.CrossRefGoogle Scholar
[10] Halperin, B. L., Feng, S. and Sen, P. N. (1985) Differences between lattice and continuum percolation transport exponents. Phys. Rev. Lett. 54, 2391–2394.CrossRefGoogle ScholarPubMed
[11] Men'Shikov, M. V., Molchanov, S. A. and Sidorenko, A. F. (1986) Percolation theory and some applications. Itogi Nauki. Tekh. 24, 53–110.Google Scholar
[12] Roy, R. (1990) The Russo-Welsh theorem and the equality of critical densities and the dual critical densities for continuum percolation on ℝ d . Ann. Prob. 18, 1563–1575.CrossRefGoogle Scholar
[13] Sidorenko, A. F. and Zuev, S. A. (1985) Continuous models of percolation theory, I, II. Theoret. Math. Phys. 62, 76–88; 253-262.Google Scholar