Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T04:12:37.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic properties of the periodogram of a discrete stationary process

Published online by Cambridge University Press:  14 July 2016

Richard A. Olshen
Richard A. Olshen*
Affiliation:
Yale University
Get access Rights & Permissions [Opens in a new window]

Extract

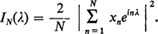Suppose x1,…, xN are indefinitely many observations on a stochastic process which is weakly stationary with spectral density f(λ), – π ≦ λ ≦ π. An asymptotically unbiased, and to that extent plausible, estimate of 4rf(λ)is the periodogram Yet the periodograms of processes which possess spectral densities are notoriously subject to erratic behavior.

Type
Research Papers
Information
Journal of Applied Probability , Volume 4 , Issue 3 , November 1967 , pp. 508 - 528
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartlett, M. S. (1962) An Introduction to Stochastic Processes. 5th printing. Cambridge U. Press.Google Scholar
Bochner, Saloman and Kawata, Tatsuo (1958) A limit theorem for the periodogram. Ann. Math. Statist. 29, 1198–1208.CrossRefGoogle Scholar
Daniell, P. J. (1946) Discussion on Symposium on autocorrelation in time series. J. R. Statist. Soc. (suppl.) 8, 88–90.Google Scholar
Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and its Applications. Vol. II. Wiley, New York.Google Scholar
Grenander, U. (1951) On empirical spectral analysis of stochastic processes. Ark. Mat. 1, 503–531.Google Scholar
Grenander, U. and Rosenblatt, M. (1957) Statistical Analysis of Stationary Time Series. Wiley, New York.CrossRefGoogle Scholar
Hannan, E. J. (1962) Time Series Analysis. 2nd printing. Methuen, London.Google Scholar
Jenkins, G. M. (1961) General considerations in the analysis of spectra. Technometrics 3, 133–166.Google Scholar
Kawata, T. (1959) Some convergence theorems for stationary stochastic processes. Ann. Math. Statist. 30, 1192–1214.Google Scholar
Kolmogorov, A. N. (1941) Stationary sequences in Hilbert space. Bul. Moscow State Univ. 2, No. 6.Google Scholar
Loève, M. (1960) Probability Theory. 2nd edition. Van Nostrand, Princeton.Google Scholar
Parzen, E. (1961) Mathematical considerations in the estimation of spectra. Technometrics 3, 167–190.Google Scholar
Rényi, A. (1958) On mixing sequences of sets. Acta Math. Acad. Sci. Hung. IX, 215–228.CrossRefGoogle Scholar
Rosenblatt, M. (1962) Random Processes. Oxford U. Press, New York.Google Scholar
Walker, A. M. (1965) Some asymptotic results for the periodogram of a stationary time series. J. Aust. Math. Soc. V, 107–128.Google Scholar
Zygmund, A. (1959) Trigonometric Series Vol. I. Cambridge U. Press.Google Scholar