Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-19T23:56:26.199Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic distribution of sum and maximum for Gaussian processes

Part of: Limit theorems Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Hwai-Chung Ho  and
William P. McCormick
Hwai-Chung Ho*
Affiliation:
Academia Sinica
William P. McCormick*
Affiliation:
University of Georgia
*
∗Postal address: Institute of Statistical Science, Academia Sinica, Taipei, Taiwan, ROC.
∗∗Postal address: Department of Statistics, University of Georgia, Athens, GA 30602, USA. Email address: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

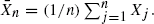Let {Xn, n ≥ 0} be a stationary Gaussian sequence of standard normal random variables with covariance function r(n) = EX0Xn. Let Under some mild regularity conditions on 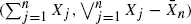r(n) and the condition that r(n)lnn = o(1) or (r(n)lnn)−1 = O(1), the asymptotic distribution of is obtained. Continuous-time results are also presented as well as a tube formula tail area approximation to the joint distribution of the sum and maximum.

Keywords

Gaussian processmaximumsumstrongly dependent

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Secondary: 60F05: Central limit and other weak theorems 60G15: Gaussian processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 36 , Issue 4 , December 1999 , pp. 1031 - 1044
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berman, S. M. (1992). Sojourns and Extremes of Stochastic Processes. Wadsworth and Brooks/Cole, Pacific Grove, CA.Google Scholar
Brockwell, P. J., and Davis, R. A. (1987). Time Series: Theory and Methods. Springer, New York.Google Scholar
Doukhan, P. (1994). Mixing, Properties and Examples (Lecture Notes in Statist. 85). Springer, New York.Google Scholar
Gray, A. (1990). Tubes. Addison-Wesley, Reading, MA.Google Scholar
Ho, H. C., and Hsing, T. (1996). On the asymptotic joint distribution of the sum and maximum of stationary normal random variables. J. Appl. Prob. 33, 138–145.CrossRefGoogle Scholar
Hsing, T. (1995). A note on the asymptotic independence of the sum and maximum of strongly mixing stationary random variables. Ann. Prob. 23, 938–947.CrossRefGoogle Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H. (1983). Extremes and Related Properties of Stationary Sequences and Processes. Springer, New York.Google Scholar
McCormick, W. P. (1980). Weak convergence for the maxima of stationary Gaussian processes using random normalization. Ann. Prob. 8, 498–510.Google Scholar
McCormick, W. P. (1999). A geometric approach to obtaining the distribution of the maximum for a class of random fields. Preprint.Google Scholar
Mittal, Y., and Ylvisaker, D. (1975). Limit distributions for the maxima of stationary Gaussian processes. Stoch. Proc. Appl. 3, 1–18.Google Scholar
Sun, J. (1993). Tail probabilities of the maxima of Gaussian random fields. Ann. Prob. 21, 34–71.CrossRefGoogle Scholar