Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T05:16:48.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour for random walks in random environments

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

S. Alili
S. Alili*
Affiliation:
Université de Cergy-Pontoise
*
∗Postal address: Département de Mathématiques, Université de Cergy-Pontoise, 2, Av. Adolphe Chauvin, 95302 Cergy-Pontoise cedex, France. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

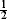In this paper we consider limit theorems for a random walk in a random environment, (Xn). Known results (recurrence-transience criteria, law of large numbers) in the case of independent environments are naturally extended to the case where the environments are only supposed to be stationary and ergodic. Furthermore, if ‘the fluctuations of the random transition probabilities around are small’, we show that there exists an invariant probability measure for ‘the environments seen from the position of (Xn)’. In the case of uniquely ergodic (therefore non-independent) environments, this measure exists as soon as (Xn) is transient so that the ‘slow diffusion phenomenon’ does not appear as it does in the independent case. Thus, under regularity conditions, we prove that, in this case, the random walk satisfies a central limit theorem for any fixed environment.

Keywords

Random walkrandom environmentbranching process

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60J85: Applications of branching processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 36 , Issue 2 , June 1999 , pp. 334 - 349
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alili, S. (1994). Comportement asymptotique d'une marche aléatoire en environnement aléatoire. C. R. Acad. Sci. Paris 319, 1207–1212.Google Scholar
Athreya, K. B., and Ney, P. E. (1972). Branching Processes. Springer, Berlin.Google Scholar
Chung, K. L. (1967). Markov Chains with Stationary Transition Probabilities, 2nd edn. Springer, New York.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and its Applications, Vol 2, 3rd edn. Wiley, New York.Google Scholar
Greven, A., and den Hollander, F. (1994). Large deviations for random walk in random environment. Ann. Prob. 22, 1381–1428.Google Scholar
Harris, T. (1952). First passage and recurrence distributions. Trans. Amer. Math. Soc. 73, 471–486.Google Scholar
Kesten, H. (1975). Sums of stationary sequences cannot grow slower than linearly. Proc. Amer. Math. Soc. 49, 205–211.CrossRefGoogle Scholar
Kesten, H. (1977). A renewal theorem for random walk in a random environment. In Probability, ed Doob, J. L. (Proc. Sympos. Pure Math. 31). AMS, Providence, RI, pp. 67–77.Google Scholar
Kesten, H., Kozlov, M. V., and Spitzer, F. (1975). A limit law for random walk in random environment. Compositio Mathematica 30, 145–168.Google Scholar
Kozlov, S. M. (1985). The method of averaging and walks in inhomogeneous environments. Russian Math. Surveys 40, 73–145.Google Scholar
Petit, B. (1975). Le théorème limite central pour des sommes de Riesz-Raikov. Prob. Theory Rel. Fields 93, 407–438.Google Scholar
Petrov, V. V. (1975). Sums of independent random variables. Ergebnisse 82, Springer, New York.Google Scholar
Solomon, F. (1975). Random walks in a random environment. Ann. Prob. 3, 1–31 Google Scholar
Temkin, D. E. (1969). A theory of diffusionless crystal growth. Kristallografiya 14, 423–430.Google Scholar