No CrossRef data available.
Article contents
Analysis of a non-reversible Markov chain speedup by a single edge
Published online by Cambridge University Press: 04 January 2023
Abstract
We present a Markov chain example where non-reversibility and an added edge jointly improve mixing time. When a random edge is added to a cycle of n vertices and a Markov chain with a drift is introduced, we get a mixing time of
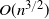 $O(n^{3/2})$
with probability bounded away from 0. If only one of the two modifications were performed, the mixing time would stay
$O(n^{3/2})$
with probability bounded away from 0. If only one of the two modifications were performed, the mixing time would stay
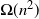 $\Omega(n^2)$
.
$\Omega(n^2)$
.
Keywords
MSC classification
Secondary:
37A25: Ergodicity, mixing, rates of mixing
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Aldous, D. and Fill, J. A. (2002). Reversible Markov Chains and Random Walks on Graphs. Unfinished monograph, recompiled 2014, available at http://www.stat.berkeley.edu/~aldous/RWG/book.html.Google Scholar
Angel, O., Peres, Y. and Wilson, D. B. (2008). Card shuffling and Diophantine approximation. Ann. Appl. Prob. 18, 1215–1231.CrossRefGoogle Scholar
Berry, A. C. (1941). The accuracy of the Gaussian approximation to the sum of independent variates. Trans. Amer. Math. Soc. 49, 122–136.CrossRefGoogle Scholar
Boczkowski, L., Peres, Y. and Sousi, P. (2018). Sensitivity of mixing times in eulerian digraphs. SIAM J. Discrete Math. 32, 624–655.CrossRefGoogle Scholar
Boyd, S., Diaconis, P., Parrilo, P. and Xiao, L. (2009). Fastest mixing Markov chain on graphs with symmetries. SIAM J. Optim. 20, 792–819.CrossRefGoogle Scholar
Diaconis, P. (2009). The Markov chain Monte Carlo revolution. Bull. Amer. Math. Soc. 46, 179–205.CrossRefGoogle Scholar
Diaconis, P., Holmes, S. and Neal, R. M. (2000). Analysis of a nonreversible Markov chain sampler. Ann. Appl. Prob. 10, 726–752.CrossRefGoogle Scholar
Esseen, C.-G. (1942). On the Liapunov limit error in the theory of probability. Arkiv für Matematik, Astronomi och Fysik 28, 1–19.Google Scholar
Gerencsér, B. (2011). Markov chain mixing time on cycles. Stoch. Process. Appl. 121, 2553–2570.CrossRefGoogle Scholar
Gerencsér, B. and Hendrickx, J. M. (2019). Improved mixing rates of directed cycles by added connection. J. Theoret. Prob. 32, 684–701.CrossRefGoogle Scholar
Jarník, V. (1928–29). Zur metrischen Theorie der diophantischen Approximationen. Prace Matematyczno-Fizyczne 36, 91–106.Google Scholar
Khintchine, A. (1924). Einige Sätze über Kettenbrüche, mit Anwendungen auf die Theorie der diophantischen Approximationen. Mathematische Annalen 92, 115–125.CrossRefGoogle Scholar
Levin, D. A. and Peres, Y. (2017). Markov Chains and Mixing Times, 2nd edn. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Spencer, J. (2014). Asymptopia. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Walfisz, A. (1963). Weylsche exponentialsummen in der neueren zahlentheorie. VEB Deutscher Verlag der Wissenschaften, Berlin.Google Scholar



