Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T16:59:24.562Z Has data issue: false hasContentIssue false
  • English
  • Français

An asymptotic result in traffic theory

Published online by Cambridge University Press:  14 July 2016

J. Gani  and
J. Lehoczky
J. Gani
Affiliation:
University of Sheffield
J. Lehoczky
Affiliation:
Carnegie-Mellon University
Get access Rights & Permissions [Opens in a new window]

Extract

In problems of traffic theory, we are frequently concerned with the queues of vehicles which form at an intersection. A standard model is the vehicle queue whose length is increased during unit time intervals [t, t + 1) by non-negative integer inputs 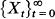which form a sequence of i.i.d. or Markovian random variables; see Gani (1970) and Lehoczky ((1969), (1971)). The output from the queue at the end of each unit of time is one vehicle if the queue is non-empty, and no vehicle if there are none waiting.

Type
Short Communications
Information
Journal of Applied Probability , Volume 8 , Issue 4 , December 1971 , pp. 815 - 820
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Daley, D. J. (1969) The total waiting time in a busy period of a stable single-server queue, I. J. Appl. Prob. 6, 550–564.Google Scholar
[2] Daley, D. J. and Jacobs, D. R. (1969) The total waiting time in a busy period of a stable single-server queue, II. J. Appl. Prob. 6, 565–572.Google Scholar
[3] Gani, J. (1969) Recent advances in storage and flooding theory. Adv. Appl. Prob. 1, 90–110.Google Scholar
[4] Gani, J. (1970) First emptiness problems in queueing, storage and traffic theory. (To appear in Proc. Sixth Berkeley Symposium.) Google Scholar
[5] Gani, J. and Mcneil, D. R. (1971) Joint distributions of random variables and their integrals for certain birth-death and diffusion processes. Adv. Appl. Prob. 3, 339–352.Google Scholar
[6] Gleser, L. J. (1965) On the asymptotic theory of fixed-size sequential confidence bounds for linear regression parameters. Ann. Math. Statist. 36, 463–467.Google Scholar
[7] Lehoczky, J. P. (1969) Stochastic models in traffic flow theory: intersection control. Stanford University Technical Report No. 20.Google Scholar
[8] Lehoczky, J. P. (1971) A note on the first emptiness time of an infinite reservoir with inputs forming a Markov chain. J. Appl. Prob. 8, 276–284.Google Scholar
[9] Vere-Jones, D. (1967) Ergodic properties of non-negative matrices, I. Pacific J. Math. 22, 361–386.Google Scholar
[10] Vere-Jones, D. (1968) Ergodic properties of non-negative matrices, II. Pacific J. Math. 26, 601–620.Google Scholar