Article contents
An alternative to Wiener-Hopf methods for the study of bounded processes
Published online by Cambridge University Press: 14 July 2016
Extract
Homogeneous additive processes on a finite or semi-infinite interval have been studied in many forms. Wald's identity for the first passage process on the finite interval (see for example Miller, 1961), the waiting time process of Lindley (1952), and a variety of problems in the theory of queues, dams, and inventories come to mind. These processes have been treated by and large by methods in the complex plane. Lindley's discrete parameter process on the continuum, for example, described by
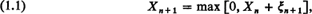 where the ξn are independent identically distributed random variables, has been discussed by Wiener-Hopf methods in recent years by Lindley (1952), Smith (1953), Kemperman (1961), Keilson (1961), and many others. A review of earlier studies is given by Kemperman.
where the ξn are independent identically distributed random variables, has been discussed by Wiener-Hopf methods in recent years by Lindley (1952), Smith (1953), Kemperman (1961), Keilson (1961), and many others. A review of earlier studies is given by Kemperman.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1964
References
A correction has been issued for this article:
- 6
- Cited by
Linked content
Please note a has been issued for this article.


