Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kemperman, J. H. B.
1973.
On Poisson type stationary mass distributions in Rn.
Advances in Applied Probability,
Vol. 5,
Issue. 1,
p.
16.
Kemperman, J. H. B.
1973.
On Poisson type stationary mass distributions in R
n.
Advances in Applied Probability,
Vol. 5,
Issue. 01,
p.
16.
De Smit, J. H. A.
1976.
A probabilistic approach to Pollaczek's integral equations for the many-server queue.
Advances in Applied Probability,
Vol. 8,
Issue. 2,
p.
243.
Malyshev, V. A.
1977.
Wiener-Hopf equations and their applications in probability theory.
Journal of Soviet Mathematics,
Vol. 7,
Issue. 2,
p.
129.
1982.
The Single Server Queue.
Vol. 8,
Issue. ,
p.
676.


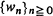 in
in 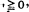 , where the variables
, where the variables 