Published online by Cambridge University Press: 27 March 2009
1. The first lactation shews greater variability than the second, third, fourth or fifth.
2. The estimation of one lactation from another cannot be made with great accuracy, since the correlation coefficient between even successive lactations does not rise above + ·6.
3. It is necessary, in classing a cow, to decide on one lactation that shall represent her mature capability. It is suggested that the maximum lactation is the most suitable one to chose.
4. The correlation coefficient with the maximum lactation increases from ·394 for first to ·762 for fifth lactation.
5. The mean of the first and second lactations however gives a correlation coefficient of ·526 with maximum lactation, which is higher than any of the first three taken separately.
page 377 note 1 In other words, the highest figure common to the three highest day-yields of a lactation.
page 377 note 2 Gavin, , “The Interpretation of Milk Records,” Journ. Roy. Agric. Soc. 1912, p. 153Google Scholar; v. also “Studies in Milk Records: Influence of Foetal Growth on Yield,” Journ. Agric. Science, 1913, Vol. V. Part 3.Google Scholar
page 378 note 1 Pearson, , Biometrika, Vol. 1. 1902, p. 260.Google Scholar
page 378 note 2 Pearson, , ‘Regression Heredity and Panmixia,” Phil. Trans. Roy. Soc. CLXXXVII. 1896, p. 276.Google Scholar
page 380 note 1 v. Interpretation of Milk Records.
page 380 note 2 Owing to the fact that all cows were not available for every correlation table, these constants shew slight variations. The actual values obtained were as follows:

page 382 note 1 Constants of variation given by this average are: Mean 11·18 quarts ± 0·071, σ 1·82 quarts ± 0·050, v 16·3 ± 0·448.
It should perhaps be emphasised that, in calculating this correlation, all available cows were used, as in the other cases. The cows used for determining the correlation of max. R. M. with R. M. of first lactation, of second lactation, and mean of first and second lactations are therefore not all the same (cf. variation in the constants for max. R. M. in the footnote on p. 380). As a consequence if we calculate the s.d. of mean R. M. of first and second lactations from the formula ![]() we get 1·73, not 1·82: and if we calculate the correlation from the formula
we get 1·73, not 1·82: and if we calculate the correlation from the formula

we get 0·500, not 0·526. By reason of the coefficients not being entirely comparable with each other, the application of the theory of partial correlation to determine a regression equation giving the deviation in max. R. M. in terms of the deviations of first and second R. M. separately is a little doubtful. Mr Yule finds the equation
xm = 0·345x 1 + 0·457x 2
where xm the deviation in max. R. M.The probable error of estimate in using this equation is only very slightly lower than the p.e. of estimate in using the mean of first and second lactations.
page 383 note 1 Regression coefficient of x relative to 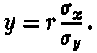 Probable error of regression coefficient
Probable error of regression coefficient 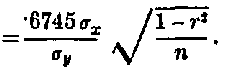
page 383 note 2 Probable error of estimate ![]()
page 384 note 1 v. Interpretation of Milk Records.
page 386 note 1 v. Interpretation of Milk Records.
page 386 note 2 The probable error of estimated lactation total is about ±61 gallons, and is expressed by the formula ![]() where (p.e.)1 is P.E. of estimate of max. R. M., (p.e.)2 the P.E. of estimate of lactation total from any R. M., and r.c. the regression of totals relative to R. M. The author is indebted to Mr G. Udoy Yule for information on this point.
where (p.e.)1 is P.E. of estimate of max. R. M., (p.e.)2 the P.E. of estimate of lactation total from any R. M., and r.c. the regression of totals relative to R. M. The author is indebted to Mr G. Udoy Yule for information on this point.