Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T16:11:16.978Z Has data issue: false hasContentIssue false
  • English
  • Français

A wideband biconic shape metasurface for polarization conversion and radar cross-section reduction

Published online by Cambridge University Press:  10 February 2025

Haseeba Kanwal ,
Babar Kamal Open the ORCID record for Babar Kamal [Opens in a new window] ,
Sadiq Ullah ,
Waleed Shihzad ,
Usman Ali ,
Amjad Aziz  and
Zakriya Faraz
Haseeba Kanwal
Affiliation:
Department of Telecommunication Engineering, University of Engineering and Technology, Mardan, Khyberpukhtoonkhwa, Pakistan
Babar Kamal*
Affiliation:
Center of Intelligent Acoustics and Immersive Communications, Northwestern Polytechnical University, Xi’an, Shaanxi, China
Sadiq Ullah
Affiliation:
Department of Telecommunication Engineering, University of Engineering and Technology, Mardan, Khyberpukhtoonkhwa, Pakistan
Waleed Shihzad
Affiliation:
Department of Telecommunication Engineering, University of Engineering and Technology, Mardan, Khyberpukhtoonkhwa, Pakistan
Usman Ali
Affiliation:
Department of Telecommunication Engineering, University of Engineering and Technology, Mardan, Khyberpukhtoonkhwa, Pakistan
Amjad Aziz
Affiliation:
Department of Telecommunication Engineering, University of Engineering and Technology, Mardan, Khyberpukhtoonkhwa, Pakistan
Zakriya Faraz
Affiliation:
Department of Telecommunication Engineering, University of Engineering and Technology, Mardan, Khyberpukhtoonkhwa, Pakistan
*
Corresponding author: Babar Kamal; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A single-layer polarization converting metasurface (PCMS) with wideband is presented for polarization conversion and radar cross-section (RCS) reduction. The proposed PCMS is composed of metallic biconic shape resonator imprinted on a metal-backed F4BM dielectric substrate of relative permittivity 2.2 and loss tangent 0.001. The unit cell has a compact size of 0.16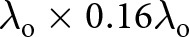$\lambda_\mathrm{o} \times 0.16\lambda_\mathrm{o}$. A comprehensive parametric analysis, angular sensitivity study, bistatic and monostatic RCS analysis are conducted by illuminating the proposed PCMS using linearly polarized (LP) plane waves. The PCMS converts LP electromagnetic waves to their orthogonal polarization state in the frequency band of 8.7–24.8 GHz resulting in polarization conversion ratio over 90% with a fractional bandwidth of 96%. Additionally, the developed structure is applied in chessboard configuration, using phase cancellation techniques for RCS reduction, that achieve 10 dB RCS reduction across a wideband of 7.9–23.4 GHz. The unit cell and its rotated version has a cross-polarization reflection phase difference of (${180}\pm {37}{^\circ}$) in the operating band, which fulfill the criteria for RCS reduction. The chessboard configuration exhibits a scattering pattern with four strong lobes that deviates from the normal incident path because of the phase cancellation in normal direction. The experimental results are in good agreement with the simulated result. Applications for the developed structure include antenna design (gain enhancement and beam steering), target hiding, imaging, and microwave communications.

Keywords

angular sensitivityfractional bandwidthlinearly polarizedmetasurfacephase cancellationPolarizationpolarization conversionradar cross sectionwideband
Type
Research Paper
Information
International Journal of Microwave and Wireless Technologies , Volume 16 , Special Issue 10: Swedish microwave days 2023 , December 2024 , pp. 1685 - 1695
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press in association with The European Microwave Association.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdullah, M, Koziel, S and Szczepanski, S (2021) Normalized partial scattering cross section for performance evaluation of low-observability scattering structures. Electronics 10(14), .Google Scholar
Kamal, B, Chen, J, Yin, Y, et al. (2020) A broad band polarization converting metasurface for c and x-band applications. In 2020 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). Hongkong: IEEE, pp. 1–4.CrossRefGoogle Scholar
Khan, TA, Li, J, Chen, J, et al. (2019) Design of a low scattering metasurface for stealth applications. Materials 12(18), .Google ScholarPubMed
Xu, J, Li, R, Qin, J, et al. (2018) Ultra-broadband wide-angle linear polarization converter based on H-shaped metasurface. Optics Express 26(16), 20913–20919.CrossRefGoogle ScholarPubMed
Zhang, Z, Wang, J, Fu, X, et al. (2021) Single-layer metasurface for ultra-wideband polarization conversion: Bandwidth extension via Fano resonance. Scientific Reports 11(1), 1–8.Google ScholarPubMed
Qi, Y, Zhang, B, Liu, C, et al. (2020) Ultra-broadband polarization conversion meta-surface and its application in polarization converter and RCS reduction. IEEE Access 8 (22), .Google Scholar
Khan, B, Ullah, S, Kamal, B, et al. (2019) An extended split ring resonator type metasurface for microwave applications. In 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST). Islamabad, Pakistan: IEEE, pp. 1046–1049.Google Scholar
Khan, B, Kamal, B, Ullah, S, et al. (2020) Design and experimental analysis of dual-band polarization converting metasurface for microwave applications. Scientific Reports 10(1), 1–13.Google ScholarPubMed
Bianmei, Z, Chen, W, Shuo, Y, Xiaofan, Y, Zhibin, F, and Xiaoming, L (2023) Dual-band transmissive linear to circular polarization converter with angular-stable and orthogonal polarizations. International Journal of Microwave and Wireless Technologies 16 (3) 1–9.Google Scholar
Mu, X, Lv, M and Ni, T (2022) Design of an ultra-broadband polarization rotating reflective surface for the reduction of radar cross section. Progress in Electromagnetics Research M 114, 69–78.Google Scholar
Hao, H, Du, S and Zhang, T (2019) Small-size broadband coding metasurface for RCS reduction based on particle swarm optimization algorithm. Progress in Electromagnetics Research M 81, 97–105.CrossRefGoogle Scholar
Tiwari, P, Pathak, SK, Vp, A, et al. (2020) X-band Γ-shaped anisotropic metasurface-based perfect cross-polarizer for RCS reduction. Journal of Electromagnetic Waves and Applications 34(7), 894–906.CrossRefGoogle Scholar
Wan, X, Xiang Jiang, W, Feng Ma, H, et al. (2014) A broadband transformation-optics metasurface lens. Applied Physics Letters 104(15), .Google Scholar
Kamal, B, Ullah, S, Khan, B, et al. (2021) Ultrathin and high efficient wideband polarization converting metasurface. International Journal of RF and Microwave Computer-Aided Engineering 31(7), .Google Scholar
Tiwari, P, Pathak, SK, and Anitha, V (2021) Design, development and characterization of wide incidence angle and polarization insensitive metasurface absorber based on resistive-ink for X and Ku band RCS reduction. Waves in Random and Complex Media 34 (4) 1–16.Google Scholar
Kamal, B, Chen, J, Yingzeng, Y, et al. (2021) High efficiency and ultra-wideband polarization converter based on an L-shaped metasurface. Optical Materials Express 11(5), 1343–1352.CrossRefGoogle Scholar
Kamal, B, Chen, J, Yin, Y, et al. (2020) Wide band cross polarization converting metasurface based on circular split rings resonators. In 2020 IEEE International Conference on Computational Electromagnetics (ICCEM). Singapore: IEEE, pp. 223–225.Google Scholar
Lin, Bq, Huang, W, Yang, Y, et al. (2022) An ultra-wideband polarization conversion metasurface for RCS reduction. Journal of Electromagnetic Waves and Applications 36(5), 597–606.Google Scholar
Ahmad, T, Rahim, AA, Bilal, RMH, et al. (2022) Ultrawideband cross-polarization converter using anisotropic reflective metasurface. Electronics 11(3), .CrossRefGoogle Scholar
Fang, C, Cheng, Y, He, Z, et al. (2017) Design of a wideband reflective linear polarization converter based on the ladder-shaped structure metasurface. Optik 137, 148–155.CrossRefGoogle Scholar
Ozturk, G (2022) Ultra-thin, wide-angle and bandwidth-enhanced linear and circular metasurface-based reflection-type polarization converter at X-band microwave frequency. Journal of Electromagnetic Waves and Applications 10 (10) 1–13.Google Scholar
Li, F, Chen, H, Zhang, L, et al. (2018) Compact high-efficiency broadband metamaterial polarizing reflector at microwave frequencies. IEEE Transactions on Microwave Theory and Techniques 67(2), 606–614.Google Scholar
Deng, G, Sun, H, Lv, K, et al. (2020) An efficient wideband cross-polarization converter manufactured by stacking metal/dielectric multilayers via 3D printing. Journal of Applied Physics 127(9), .Google Scholar
Xi, Y, Jiang, W, Hong, T, et al. (2021) Wideband and wide-angle radar cross section reduction using a hybrid mechanism metasurface. Optics Express 29(14), 22427–22441.CrossRefGoogle ScholarPubMed
Su, J, He, H, Li, Z, et al. (2018) Uneven-layered coding metamaterial tile for ultra-wideband RCS reduction and diffuse scattering. Scientific Reports 8(1), 1–9.CrossRefGoogle ScholarPubMed
Ameri, E, Esmaeli, SH and Sedighy, SH (2019) Ultra wideband radar cross section reduction by using polarization conversion metasurfaces. Scientific Reports 9(1), 1–8.Google ScholarPubMed
Ameri, E, Esmaeli, SH and Sedighy, SH (2018) Low cost and thin metasurface for ultra wide band and wide angle polarization insensitive radar cross section reduction. Applied Physics Letters 112(20), .Google Scholar
Zheng, Q, Guo, C, Li, H, et al. (2018) Broadband radar cross-section reduction using polarization conversion metasurface. International Journal of Microwave and Wireless Technologies 10(2), 197–206.Google Scholar
Deng, ZH, Wang, FW, Ren, YH, et al. (2019) A novel wideband low-RCS reflector by hexagon polarization rotation surfaces. IEEE Access 7, 131527–131533.Google Scholar
Chatterjee, J, Mohan, A and Dixit, V (2021) Radar cross section reduction and gain enhancement of slot antenna using polarization conversion metasurface for X-band applications. International Journal of RF and Microwave Computer-Aided Engineering 31(10), .CrossRefGoogle Scholar
Kamal, B, Chen, J, Yin, Y, et al. (2022) Broad-band and broad-angle linear and circular polarization converting metasurface. Journal of Electromagnetic Waves and Applications 36(8), 1102–1112.Google Scholar
Kamal, B, Khan, B, Chen, J, Yin, Y, et al. (2023) Ultra-thin wideband polarization converting metasurface for complete KU and K bands microwave applications Zhengzhou, China: IEEE, 1–4. In 2023 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC).CrossRefGoogle Scholar
Yao, M, Jianbo, W, Lihua, S, Shuyun, X, Yuzhou, R, Jie, L and Yicheng, L (2021) Ultra-wideband, optically transparent, and flexible microwave metasurface absorber. Optical Materials Express 11(7), 2206–2217.Google Scholar
Priyanka, T, Surya, KP, and Siju, V (2022) Development of resistive-ink based planar and conformal metasurfaces for RCS reduction. IEEE Access 10 (2), 61472–61483Google Scholar
Abbasi, QH, Abbas, HT, Alomainy, A and Imran, MA (2021) Backscattering and RF Sensing for Future Wireless Communication. John Wiley & Sons.Google Scholar
Fu, C, Han, L, Liu, C, et al. (2020) Dual-band polarization conversion metasurface for RCS reduction. IEEE Transactions on Antennas and Propagation 69(5), 3044–3049.Google Scholar
Lu, J, Cao, X, Gao, J, et al. (2021) Low RCS reflective polarization conversion metasurface. In 2021 International Conference on Microwave and Millimeter Wave Technology (ICMMT). Nanjing, China: IEEE, pp. 1–3.Google Scholar
Zhang, Z, Cao, X, Gao, J, et al. (2018) Wideband radar cross section reduction using polarization conversion metasurface. In 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT). Chengdu, China: IEEE, pp. 1–3.CrossRefGoogle Scholar
Shu, Y, Zhang, Y, He, S, et al. (2018) An ultra-wideband metasurface for RCS reduction. In 2018 International Applied Computational Electromagnetics Society Symposium-China (ACES). Beijing, China: IEEE, pp. 1–2.CrossRefGoogle Scholar
Zheng, Q, Li, Y, Zhang, J, et al. (2017) Wideband, wide-angle coding phase gradient metasurfaces based on pancharatnam-berry phase. Scientific Reports 7(1), .Google Scholar
Jia, Y, Liu, Y, Guo, YJ, et al. (2015) Broadband polarization rotation reflective surfaces and their applications to RCS reduction. IEEE Transactions on Antennas and Propagation 64(1), 179–188.CrossRefGoogle Scholar