Introduction
The study of bi-isotropic (BI) media has many interesting applications in the theory of wave propagation and scattering [Reference Lakhtakia1–Reference Paiva, Topa and Barbosa12]. It is known that a BI medium is bi-refringent due to the chiral nature of the medium and bi-impedant due to the nonreciprocal nature of the Tellegen medium [Reference Lindell, Sihvola, Tretyakov and Viitanen2]. The wave propagation in various BI media including unbounded [Reference Ougier, Chenerie, Sihvola and Priou3], half space [Reference Lindell, Sihvola and Viitanen4], and multilayered slab [Reference He and Hu5] has been studied. The radiation and scattering in a homogeneous general BI media have been studied by Monzon [Reference Monzon6]. The scattering characteristics of BI objects have been studied by Monzon [Reference Monzon7] and He et al. [Reference He and Cao8]. Recently, Monzon and Forester [Reference Monzon and Forester9] have investigated that BI media are capable of generating negative refraction for circularly polarized waves. Various types of waveguides filled with BI media have been studied in [Reference Koivisto, Tretyakov and Oksanen10–Reference Paiva, Topa and Barbosa12]. Tellegen medium is a medium that can be identified as a subclass of BI media and first proposed by Tellegen [Reference Tellegen13]. It is noted by Astrov [Reference Astrov14] that a Tellegen medium is identified by a spontaneous nonreciprocal magnetoelectric coupling. He also concluded that Chromium oxide is a natural example of such Tellegen medium. Later on, some debate on the existence of such a Tellegen medium has been started by some authors, see for example [Reference Lakhtakia15–Reference Sihvola, Tretyakov, Serdyukov and Semchenko17]. After this, the Tellegen media have attracted the attention of some scientists [Reference Mong, Essin and Moore18, Reference Predencio, Matos and Paiva19].
Nowadays, there is a growing interest in the new class of materials called perfect electromagnetic conductor (PEMC) as introduced by Lindell and Sihvola [Reference Lindell and Sihvola20, Reference Lindell and Sihvola21]. It is the generalization of perfect electric conductor (PEC) and perfect magnetic conductor (PMC) material and isotropic in nature. The PEMC material is characterized by an admittance parameter M. The interaction of electromagnetic waves with the various PEMC geometries has been studied by many authors and has potential applications in wave propagation [Reference Lindell and Sihvola22], resonators [Reference Lindell and Sihvola23], and scattering from cylindrical targets [Reference Ruppin24, Reference Ahmed and Naqvi25]. The realization of a PEMC planar boundary has been proposed by Lindell and Sihvola [Reference Lindell and Sihvola26]. Later on, many researchers discussed the realization of PEMC material [Reference Shahvarpour, Kodera, Parsa and Caloz27–Reference Caloz, Shahvarpour, Sounas, Kodera, Gurlek and Chamanara29]. According to the authors, the scattering characteristics of a general BI layer–coated PEMC cylindrical object has not been reported previously in the literature and has been studied in this paper.
In this paper, scattering characteristics of a PEMC cylindrical object covered with a general BI layer has been investigated. To solve the problem, we have used a cylindrical vector wave function (CVWF) expansion approach along with the applications of tangential boundary conditions. Analytic expressions of the scattering coefficients have been derived in the simplest forms, which have not been reported previously. The influences of various parameters including admittance of PEMC cylinder, chirality, and Tellegen parameter of BI coating and coating thickness upon the co- and cross-polarized scattering widths (SW) have been studied. It is investigated that the specific types of BI and strong chiral-coated PEMC cylindrical rods having certain coating thicknesses can be used to suppress the cross-polarized forward scattering while enhancing the co-polarized forward scattering significantly. It is also found that the chiral nihility coating can be used to suppress the cross-polarized scattering characteristics of a PEMC cylindrical object. Some special cases have been discussed and shown, where co-polarized and cross-polarized backscattering have been suppressed. Enhanced co-polarized forward scattering finds applications in point-to-point communication, whereas the suppressed co-polarized and cross-polarized backscattering is helpful in the design of radar engineering problems and stealth technology. These proposed findings are novel and have not been reported previously in the literature.
Electromagnetic scattering from a BI-coated PEMC cylindrical object
An infinite circular cylindrical object made of PEMC material whose axis is parallel to z-axis is considered. It is well known that for a PEMC material, the controlling parameter is the admittance parameter M. If 
$M\rightarrow \pm\infty$, then PEMC material reduces to a PEC material, and if M = 0, then we have equivalently PMC material. This PEMC cylinder is covered with a BI layer. The inner radius of a PEMC core cylinder is taken to be a, whereas the radius of outer BI coating is assumed to be b. The time dependency for the problem under study is taken to be 
${\rm e}^{j\omega t}$ and has been suppressed throughout. This BI-coated cylinder is placed in the free space medium whose propagation constant is 
$k_{0}=\omega\sqrt{\mu_{0}\epsilon_{0}}$. Here µ 0 and ϵ 0 represent the permeability and permittivity of the free space, respectively. The considered geometry of the problem has been shown in Fig. 1.
Figure 1. The geometrical configuration of the BI-coated PEMC cylindrical object placed in the free space background medium. The upper panel shows lateral view, whereas the lower panel represents cross-sectional view.
There exists various formalisms for constitutive relations of the general homogeneous and isotropic BI medium in the literature, see for example [Reference Ougier, Chenerie, Sihvola and Priou3]. For the present study, the constitutive relations of the BI medium as adopted by Lindell et al. [Reference Lindell, Sihvola, Tretyakov and Viitanen2] have been used. These constitutive relations consist of four material parameters, and they are ϵr, µr, κr, and χr. Here ϵr and µr represent relative permittivity and relative permeability of the BI medium, respectively. Likewise, κr represents chirality parameter and χr is known as a Tellegen parameter of the BI medium. The BI medium is in general bi-refringent and bi-impedant. The birefringence nature of the BI medium is associated with non-zero value of chirality κr, whereas the bi-impedant nature of the BI medium is associated with non-zero value of Tellegen parameter χr. Due to inherent birefringence nature of the BI medium, there exists two types of circularly polarized waves inside it. One of the wave is called right circularly polarized (RCP) wave, and other one is named as left circularly polarized (LCP) wave. These two waves are associated with two different wave numbers kr, kl and two different wave impedances ηr, ηl, which are given as follows [Reference Ougier, Chenerie, Sihvola and Priou3, Reference Awan30],
\begin{equation}
k_{r}=k_{0}n_{r}, \qquad k_{l}=k_{0}n_{l}.
\end{equation}
\begin{align}
n_{r} &= \sqrt{\epsilon_{r}\mu_{r}}(\sqrt{1-\chi_{r}^{2}}+\kappa_{r}), \nonumber\\
n_{l} &= \sqrt{\epsilon_{r}\mu_{r}}(\sqrt{1-\chi_{r}^{2}}-\kappa_{r}).
\end{align}
\begin{align}
\eta_{r}&= \eta_{0}\sqrt{\mu_{r}/\epsilon_{r}}(\sqrt{1-\chi_{r}^{2}}-j\chi_{r}), \nonumber\\
\eta_{l} &= \eta_{0}\sqrt{\mu_{r}/\epsilon_{r}}(\sqrt{1-\chi_{r}^{2}}+j\chi_{r}).
\end{align} Here nr, nl are refractive indices associated with RCP and LCP waves, respectively. Likewise, the wave impedance for RCP wave is ηr, whereas the wave impedance for LCP wave is ηl. Also η 0 is the intrinsic impedance of the free space. It should be noted that if 
$\chi_{r} = 0$ and 
$\kappa_{r}\neq 0$, then the equivalent BI medium is taken to be a chiral medium. Likewise, if 
$\kappa_{r} = 0$ and 
$\chi_{r}\neq 0$, then this BI medium reduces to an equivalent Tellegen medium.
Due to cylindrical symmetry of the considered problem as given in Fig. 1, the electromagnetic field vectors in various regions can be defined in terms of CVWFs as given by Kluskens and Newman [Reference Kluskens and Newman31], and they can be written as,
\begin{equation}
\mathbf{N}_{n}^{(q)}(k\rho)=\hat{\mathbf{z}}Z_{n}^{(q)}(k\rho){\rm e}^{jn\phi},
\end{equation}
\begin{equation}
\mathbf{M}_{n}^{(q)}(k\rho)=\hat{{\rho}}\frac{jn}{k\rho}Z_{n}^{(q)}(k\rho){\rm e}^{jn\phi}-\hat{{\phi}}Z_{n}^{(q)\prime}(k\rho){\rm e}^{jn\phi},
\end{equation}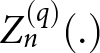
$Z_{n}^{(q)}(.)$ represents Bessel function of type q and order n with 
$Z_{n}^{(1)} = J_{n}(\cdot)$, 
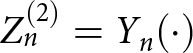$Z_{n}^{(2)}= Y_{n}(\cdot)$, and 
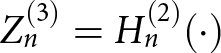$Z_{n}^{(3)} = H_{n}^{(2)}(\cdot)$. The function 
$J_{n}(\cdot)$ is the Bessel function of first kind having order n. Likewise, 
$Y_{n}(\cdot)$ represents the Bessel function of second kind with order n, and 
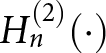$H_{n}^{(2)}(\cdot)$ is the nth-order Hankel function of second kind.
It is assumed that an incident wave is propagating along the negative x-axis and has its electric field parallel to z-axis, impinging upon the considered BI-coated PEMC cylindrical object. This is shown in the lower panel of Fig. 1. This type of incident wave can be taken as a normally incident transverse magnetic (TM) wave with respect to the z-axis. Thus, the incident electric field vector 
$\mathbf{E}^{\rm inc}$ and incident magnetic field vector 
$\mathbf{H}^{\rm inc}$ can be expanded in terms of CVWFs as,
\begin{equation}
\mathbf{E}^{\rm inc}=\hat{\mathbf{z}}E_{0}\,{\rm e}^{-jk_{0}x}=E_{0}\sum_{n=-\infty}^{n=+\infty}j^{-n}\mathbf{N}_n^{(1)}(k_{0}\rho),
\end{equation}
\begin{equation}
\mathbf{H}^{\rm inc}=\frac{j}{\eta_{0}}E_{0}\sum_{n=-\infty}^{n=+\infty}j^{-n}\mathbf{M}_{n}^{(1)}(k_{0}\rho),
\end{equation}
$\mathbf{E}^{\rm sc}$ and the scattered magnetic field vector 
$\mathbf{H}^{\rm sc}$ in the background medium. Because of the presence of BI layer, the scattered electric and magnetic fields in the background medium have both transverse electric and TM components instead of only TM component. Therefore, the scattered electric and magnetic field vectors in terms of CVWFs can be expressed as follows:
\begin{equation}
\mathbf{E}^{\rm sc}=E_{0}\sum_{n=-\infty}^{n=+\infty}j^{-n}[A_{n}\mathbf{N}_{n}^{(3)}(k_{0}\rho)+B_{n}\mathbf{M}_{n}^{(3)}(k_{0}\rho)],
\end{equation}
\begin{equation}
\mathbf{H}^{\rm sc}=\frac{j}{\eta_{0}}E_{0}\sum_{n=-\infty}^{n=+\infty}j^{-n}[A_{n}\mathbf{M}_{n}^{(3)}(k_{0}\rho)+B_{n}\mathbf{N}_{n}^{(3)}(k_{0}\rho)].
\end{equation} In Eqs. (8) and (9), An and Bn are unknown scattering coefficients and needed to be determined. Here coefficient An represents the co-polarized scattering coefficient, whereas coefficient Bn represents the cross-polarized scattering coefficient. Likewise, the electric field vector 
$\mathbf{E}^{\rm c}$ and magnetic field vector 
$\mathbf{H}^{\rm c}$ inside the BI coating layer can be expanded in terms of CVWFs as follows [Reference Awan30, Reference Kluskens and Newman31]:
\begin{align}
\mathbf{E}^{\rm c}&= E_{0}\sum_{n=-\infty}^{n=+\infty}j^{-n}\left[C_{n}\left(\mathbf{M}_{n}^{(1)}(k_{r}\rho)+\mathbf{N}_{n}^{(1)}(k_{r}\rho)\right)\right. \nonumber\\
&\qquad +D_{n}\left(\mathbf{M}_{n}^{(1)}(k_{l}\rho)-\mathbf{N}_{n}^{(1)}(k_{l}\rho)\right)+ F_{n}\left(\mathbf{M}_{n}^{(2)}(k_{r}\rho)\right.\nonumber\\
&\qquad \left.\left.+\mathbf{N}_{n}^{(2)}(k_{r}\rho)\right)+G_{n}\left(\mathbf{M}_{n}^{(2)}(k_{l}\rho)-\mathbf{N}_{n}^{(2)}(k_{l}\rho)\right)\right],
\end{align}
\begin{align}
\mathbf{H}^{\rm c}&= jE_{0}\sum_{n=-\infty}^{n=+\infty}j^{-n}\left[\frac{C_{n}}{\eta_{r}}\left(\mathbf{M}_{n}^{(1)}(k_{r}\rho)+\mathbf{N}_{n}^{(1)}(k_{r}\rho)\right)\right.\nonumber\\
&\qquad -\frac{D_{n}}{\eta_{l}}\left(\mathbf{M}_{n}^{(1)}(k_{l}\rho)-\mathbf{N}_{n}^{(1)}(k_{l}\rho)\right) +\frac{F_{n}}{\eta_{r}}\left(\mathbf{M}_{n}^{(2)}(k_{r}\rho)\right.\nonumber\\
&\qquad \left.\left.+\mathbf{N}_{n}^{(2)}(k_{r}\rho)\right)-\frac{G_{n}}{\eta_{l}}\left(\mathbf{M}_{n}^{(2)}(k_{l}\rho)-\mathbf{N}_{n}^{(2)}(k_{l}\rho)\right)\right].
\end{align}Here Cn, Dn, Fn, and Gn are unknown expansion coefficients of the BI coating layer. All these six unknown coefficients, i.e., An, Bn, Cn, Dn, Fn, and Gn can be found by applying the tangential boundary conditions at interfaces ρ = a and ρ = b, respectively. For ρ = a interface, these tangential boundary conditions can be written as,
\begin{equation}
\hat{{\rho}}\times \left(\mathbf{H}^{\rm c}+M\mathbf{E}^{\rm c}\right) = 0,
\end{equation}and for ρ = b interface, we have
\begin{align}
\hat{{\rho}}\times \left(\mathbf{E}^{\rm inc}+\mathbf{E}^{\rm sc}-\mathbf{E}^{\rm c}\right) = 0,
\end{align}
\begin{align}
\hat{{\rho}}\times \left(\mathbf{H}^{\rm inc}+\mathbf{H}^{\rm sc}-\mathbf{H}^{\rm c}\right) = 0.
\end{align}Substituting Eqs. (6)–(11) in Eqs. (12)–(14) and solving the resulting linear system of equations, the unknown six coefficients can be found. Once these unknown coefficients are known, then the electric and magnetic field vectors in each region can be found using Eqs. (6)–(11). For the present study, the unknown scattering coefficients An and Bn are of an interest. The simplest analytical forms of these scattering coefficients after some lengthy and tedious calculations are given below and have not been reported previously in the literature.
\begin{equation}
A_{n} = \frac{N_{A_{n}}}{\Delta_{n}}, \qquad B_{n} = \frac{N_{B_{n}}}{\Delta_{n}},
\end{equation}
\begin{align}
N_{A_{n}} &= \frac{2}{\pi x_{l}}\eta^{2}_{r}\left(\eta^{2}J_{n}(x_{0})H_{n}^{(2)\prime}(x_{0})-\eta^{2}_{l}J_{n}^\prime(x_{0})H^{(2)}_{n}(x_{0})\right) \nonumber\\
& \quad \cdot X_{1}+\frac{2}{\pi x_{r}}\eta^{2}_{l}\left(\eta^{2}_{r}J_{n}^\prime(x_{0})H^{(2)}_{n}(x_{0})-\eta^{2}J_{n}(x_{0})\right. \nonumber\\ & \quad \left.\cdot H_{n}^{(2)\prime}(x_{0})\right)X_{2}+\eta_{l}\eta_{r}\left(\eta^{2}J_{n}(x_{0})H_{n}^{(2)\prime}(x_{0})\right.\nonumber\\
&\quad \left.+\eta_{l}\eta_{r}J_{n}^\prime(x_{0})H^{(2)}_{n}(x_{0})\right)\left\{X_{3}X_{7}+X_{4}X_{8}+X_{5}X_{10}\right. \nonumber\\
&\quad \left.+X_{6}X_{9} \right\} - \eta\eta_{l}\eta_{r}\cdot(\eta_{l}+\eta_{r})\left[J_{n}(x_{0})H^{(2)}_{n}(x_{0})\right.\nonumber\\
&\quad \cdot \left\{X_{3}X_{8}+X_{6}X_{10}\right\}+ J_{n}^\prime(x_{0})H_{n}^{(2)\prime}(x_{0}) \nonumber\\
&\quad \left.\cdot \left\{X_{2}X_{7}+X_{5}X_{9} \right\}\right],
\end{align}
\begin{align}
N_{B_{n}} &= \frac{2j}{\pi x_{0}}\eta\eta_{l}\eta_{r}\left[\eta_{r}\left\{\frac{2}{\pi x_{l}}X_{1}-X_{3}X_{7}-X_{5}X_{10}\right\}\right. \nonumber\\
& \quad \left.+\eta_{l}\left\{\frac{2}{\pi x_{r}}X_{2} + X_{4}X_{8}+X_{6}X_{9}\right\}\right],
\end{align}
\begin{align}
\Delta_{n} &= H^{(2)}_{n}(x_{0})H^{(2)\prime}_{n}(x_{0})\left[\eta^{2}_{r}(\eta_{l}^{2}-\eta^{2})\frac{2}{\pi x_{l}}X_{1}\right.\nonumber\\
& \quad +\eta^{2}_{l}(\eta^{2}-\eta_{r}^{2})\frac{2}{\pi x_{r}}X_{2}-\eta_{l}\eta_{r}(\eta^{2}+\eta_{l}\eta_{r})\nonumber\\
& \quad \left.\cdot\left\{X_{3}X_{7}+X_{4}X_{8}+ X_{5}X_{10}+X_{6}X_{9}\right\}\right] \nonumber\\
& \quad + \eta\eta_{l}\eta_{r}(\eta_{l}+\eta_{r})\left[\left(H^{(2)\prime}_{n}(x_{0})\right)^{2}\left\{X_{4}X_{7}\right.\right. \nonumber\\ &\quad \left.\left.+X_{5}X_{9}\right\}+ \left(H^{(2)}_{n}(x_{0})\right)^{2}\left\{X_{3}X_{8}+X_{6}X_{10}\right\}\right]
\end{align}
\begin{align}
X_{1} &= Q^{+}_{n}(\eta_{r},z_{r},1)Q^{+\prime}_{n}(\eta_{r},z_{r},2)-Q^{+}_{n}(\eta_{r},z_{r},2)\nonumber\\
& \quad \cdot Q^{+\prime}_{n}(\eta_{r},z_{r},1),
\end{align}
\begin{align}
X_{2} &= Q^{-}_{n}(\eta_{l},z_{l},2)Q^{-\prime}_{n}(\eta_{l},z_{l},1)-Q^{-}_{n}(\eta_{l},z_{l},1)\nonumber\\
& \quad \cdot Q^{-\prime}_{n}(\eta_{l},z_{l},2),
\end{align}
\begin{align}
X_{3} = J_{n}^\prime(x_{r})Q^{+}_{n}(\eta_{r},z_{r},2)-Y_{n}^\prime(x_{r})Q^{+}_{n}(\eta_{r},z_{r},1),
\end{align}
\begin{align}
X_{4} = J_{n}(x_{r})Q^{+}_{n}(\eta_{r},z_{r},2)-Y_{n}(x_{r})Q^{+}_{n}(\eta_{r},z_{r},1),
\end{align}
\begin{equation}
X_{5} = J_{n}(x_{l})Q^{-}_{n}(\eta_{l},z_{l},2)-Y_{n}(x_{l})Q^{-}_{n}(\eta_{l},z_{l},1),
\end{equation}
\begin{equation}
X_{6} = J_{n}^\prime(x_{l})Q^{-}_{n}(\eta_{l},z_{l},2)-Y_{n}^\prime(x_{l})Q^{-}_{n}(\eta_{l},z_{l},1),
\end{equation}
\begin{equation}
X_{7} = J_{n}(x_{l})Q^{-\prime}_{n}(\eta_{l},z_{l},2)-Y_{n}(x_{l})Q^{-\prime}_{n}(\eta_{l},z_{l},1),
\end{equation}
\begin{equation}
X_{8} = J_{n}^\prime(x_{l})Q^{- \prime}_{n}(\eta_{l},z_{l},2)-Y_{n}^\prime(x_{l})Q^{- \prime}_{n}(\eta_{l},z_{l},1),
\end{equation}
\begin{equation}
X_{9} = J_{n}(x_{r})Q^{+ \prime}_{n}(\eta_{r},z_{r},2)-Y_{n}(x_{r})Q^{+ \prime}_{n}(\eta_{r},z_{r},1),
\end{equation}
\begin{equation}
X_{10} = J_{n}^\prime(x_{r})Q^{+ \prime}_{n}(\eta_{r},z_{r},2)-Y_{n}^\prime(x_{r})Q^{+ \prime}_{n}(\eta_{r},z_{r},1),
\end{equation}
\begin{equation}
Q^{\pm}_{n}(\eta,z,q) = (1/\eta)(j\pm M\eta)Z_{n}^{(q)}(z),
\end{equation}
$x_{l} = k_{l}b$, 
$x_{r} = k_{r}b$, 
$x_{0} = k_{0}b$, 
$z_{l} = k_{l}a$, and 
$z_{r} = k_{r}a$. In a specific case, if we take 
$\eta_{l} = \eta_{r} = \eta_{0}$, 
$k_{r} = k_{l} = k_{0}$, and a = b, then the equivalent problem reduces to the wave scattering from a PEMC cylinder having radius a with the free space background. By using this information in Eqs. (15)–(29), it can be shown that the scattering coefficients An and Bn become as follows:
\begin{align}
A_{n} = -\frac{J^{\prime}_{n}(z_{0})H^{\,(2)}_{n}(z_{0})+M^{2}\eta^{2}_{0}J_{n}(z_{0})H^{(2)\prime}_{n}(z_{0})}{(1+M^{2}\eta^{2}_{0})H^{\,(2)}_{n}(z_{0})H^{(2)\prime}_{n}(z_{0})}
\end{align}
\begin{align}
B_{n} = \frac{2 M\eta_{0}}{\pi z_{0}(1+M^{2}\eta^{2}_{0})H^{(2)}_{n}(z_{0})H^{(2)\prime}_{n}(z_{0})},
\end{align}
$z_{0} = k_{0}a$, and these scattering coefficients are consistent with Ruppin [Reference Ruppin24]. Likewise, if we take 
$M\rightarrow \infty$ in Eqs. (30) and (31), then cross polarized coefficient Bn vanishes and An becomes same as given by Balanis [Reference Balanis32], i.e., 
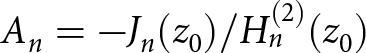$A_{n} = -J_{n}(z_{0})/H^{(2)}_{n}(z_{0})$. On the other hand, for an equivalent PMC cylinder, we have M = 0. Thus, by taking M = 0 in Eqs. (30) and (31), it is clear that again cross-polarized coefficient Bn vanishes and An becomes consistent with Ruppin [Reference Ruppin24], i.e., 
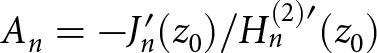$A_{n} = -J^{\prime}_{n}(z_{0})/H^{(2)\prime}_{n}(z_{0})$.
For scattering theory related to infinite cylindrical object, the bistatic echo width or SW is the quantity of an interest [Reference Balanis32]. Therefore, the scattering characteristics of a BI-coated PEMC cylindrical object has been expressed in terms of SW. Here we have two components of SWs, i.e., co-polarized and cross-polarized SWs, and they are represented by σ co and σ cross, respectively. In normalized form, they are expressed as,
\begin{equation}
\sigma_{n}^{\rm co} = \frac{\sigma_{\rm co}}{\lambda_0}=\frac{2}{\pi}\left\vert{\sum_{n=-\infty}^{n=+\infty}A_{n}\,{\rm e}^{jn\phi}}\right\vert^{2},
\end{equation}
\begin{equation}
\sigma_{n}^{\rm cr} = \frac{\sigma_{\rm cross}}{\lambda_0}=\frac{2}{\pi}\left\vert{\sum_{n=-\infty}^{n=+\infty}B_{n}\,{\rm e}^{jn\phi}}\right\vert^{2},
\end{equation}Numerical results
In this section, numerical results along with their discussions are presented. In order to validate the proposed theory, it is assumed that M tends to 
$\infty$ so that the PEMC core becomes equivalent to a PEC core, and also by taking 
$\epsilon_{r} = 9.8$, 
$\mu_{r} = 1$, and 
$\kappa_{r} = \chi_{r} = 0$, the BI coating becomes a dielectric coating. Likewise, it is assumed that a = 50 mm and b = 100 mm at an operating wavelength of 300 mm. These above electromagnetic and geometrical parameters have been adopted from Li and Shen [Reference Li and Shen33]. It is clear from Fig. 2(a) that the co-polarized SW is in excellent agreement with that of SW given by Li and Shen. Also the cross-polarized SW vanishes, which is expected and explained below. In case of a dielectric-coated PEC cylinder as considered by Li and Shen, it can be shown from Eqs. (15)–(29) that the cross-polarized scattering coefficient Bn becomes zero and hence the cross-polarized SW vanishes. This is because of the dielectric coating and PEC core, which do not give rise to the cross-polarized scattering. This can be further explained as follows. It should be noted that for 
$\chi_{r} = 0$, the cross-polarized scattering coefficient Bn as given by Eqs. (15)–(29) does not vanish and is mainly dependent upon κr and M. In this special case, if we take 
$M\rightarrow\pm\infty$ and 
$\kappa_{r}\neq 0$, then Bn does not vanish and is mainly dependent upon the chirality parameter κr. Likewise, for the same special case, if we take 
$\kappa_{r} = 0$ and 
$M\neq \pm\infty$, then once again we have a nonvanishing value of Bn, which is mainly dependent upon M. On the other hand, if we take 
$k_{r} = 0$ and 
$M\rightarrow\pm\infty$, then the cross-polarized scattering coefficient Bn vanishes, which is the case of a cylindrical scatterer adopted by Li and Shen. That is why the cross-polarized SW has not been discussed and shown by Li and Shen. Thus, it is concluded that the cross-polarized SW based on the proposed theory for a dielectric-coated PEC cylinder vanishes and is in excellent agreement with the cross-polarized SW of Li and Shen. These cross-polarized SWs have been shown in Fig. 2(a). On the other hand, if we take PEC core and 
$\chi_{r} = 0$ in the proposed formulation, then the equivalent cylindrical object becomes a chiral-coated PEC cylinder. In this case, we adopt the electromagnetic and geometrical parameters as given by Awan [Reference Awan34] in the proposed formulation. It is again found from Fig. 2(b) that the co- and cross-polarized SW results are in very good agreement with those reported by Awan. These agreements validate the proposed theory presented in the current paper.
Figure 2. Normalized scattering widths of (a) dielectric-coated PEC cylinder as given by Li and Shen and (b) chiral-coated PEC cylinder as given by Awan. These normalized scattering widths have been compared with their respective scattering widths based on the proposed theory.
It should be noted that for all BI media considered in this section except Fig. 13, we have assumed that 
$\kappa^{2}_{r} + \chi^{2}_{r} \lt 1$ [Reference Lindell, Sihvola, Tretyakov and Viitanen2]. This condition ensures that refractive indices nr and nl as given by Eq. (2) are positive. Likewise, for a chiral nihility media, it is assumed that 
$\epsilon_{r}\approx 0$, 
$\mu_{r}\approx 0$, 
$\chi_{r} = 0$, and 
$\kappa_{r}\neq 0$ as given by authors [Reference Qiu, Burokur, Zouhdi and Li35, Reference Awan36]. For the present study, we have assumed 
$\epsilon_{r} = \mu_{r} = 10^{-6}$ and 
$\kappa_{r} = 0.7$ for the considered chiral nihility coatings. On the other hand, for a chiral medium having positive refractive indices, we must have 
$\kappa^{2}_{r} \lt 1$, and this condition has been used for the chiral coatings considered here. If we have 
$\kappa^{2}_{r} \gt 1$, then such type of chiral medium is known as a strong chiral medium and is a well known concept in the literature [Reference Zhang and Cui37]. The realization of such strong chiral media has been discussed by some authors [Reference Shi, Li, Sang, Xiang, Li, Zhang and Zhang38, Reference Hou, Li, Gu and Zhang39]. For strong chiral media, we have taken fixed value of chirality, i.e., 
$\kappa_{r} = 1.5$, but ϵr and µr may vary.
In order to study the influences of various coating and core materials upon the co- and cross-polarized SW patterns of coated cylinders, we have used the same geometrical parameters as adopted by Li and Shen with fixed values of ϵr, µr, i.e., 
$\epsilon_{r} = 9.8$ and 
$\mu_{r} = 1$ for all considered coatings in Figs. 3 and 4. For a BI coating, we have 
$\kappa_{r} = \chi_{r} = 0.7$. For a chiral coating, it is assumed that 
$\kappa_{r} = 0.7$, whereas for a Tellegen coating, we have 
$\chi_{r} = 0.7$. In case of a PEMC core, it is assumed that 
$M\eta_{0} = 5$. It is important to note that the angle 
$\phi = 0^{\circ}$ corresponds to the co- and cross-polarized forward scattering width (FSW). Likewise, the angle 
$\phi = 180^{\circ}$ corresponds to the co- and cross-polarized backward scattering width (BSW). In scattering theory, the forward and backward scattering directions have significant importance. For example, forward scattering direction is important for point-to-point communication and backward scattering direction finds applications in radar engineering problems. It is studied from Fig. 3 that the maximum co-polarized SW in the forward direction is observed for a Tellegen-coated PEMC cylinder, whereas the maximum value of cross-polarized SW in the forward direction is found for a Tellegen-coated PEC cylinder. The highest value of the co-polarized BSW is 2.2407 or 3.5 dB and is observed for a Tellegen-coated PEMC cylindrical object.
Figure 3. The co- and cross-polarized scattering widths of (a, b) dielectric-coated, (c, d) BI-coated, and (e, f) Tellegen-coated cylinders with various core materials, including PEC, PMC, and PEMC.
Figure 4. The co- and cross-polarized scattering widths of various chiral coatings including (a, b) chiral, (c, d) chiral nihility, and (e, f) strong chiral for PEC, PMC, and PEMC cylindrical core materials.
The co- and cross-polarized SWs of various chiral coatings including chiral nihility and strong chiral with PEC, PMC, and PEMC cylindrical cores have been shown in Fig. 4. It is found from Fig. 4(a, b) that in case of a chiral coating, the co-polarized SW patterns of chiral-coated PEC and PEMC cylinders have no noticeable changes. For a chiral nihility coating as given in Fig. 4(c, d), the co-polarized SW patterns of chiral nihility-coated PEC and PEMC cylinders are almost same and seems to be independent of observation angle ϕ. In case of a chiral nihility-coated PEMC cylindrical object, the cross-polarized SW is very small and independent of observation angle. This observation angle independent nature of cross-polarized SW may lead to an isotropic pattern. This is an interesting result, which shows that the chiral nihility coating can be used to suppress the cross-polarized scattering characteristics of a PEMC cylindrical object. Figure 4(e, f) deal with a strong chiral coating. It is studied that the highest value of the co-polarized FSW is observed for a strong chiral-coated PMC cylinder, which is equal to 12.5 or 11 dB. Thus, it is concluded from the above analysis that the highest co-polarized FSW is observed for a strong chiral-coated PMC cylindrical object and the highest cross-polarized FSW is found for a chiral-coated PMC cylindrical object among all the other coated cylindrical objects considered in Figs. 3 and 4.
It is already mentioned previously that in scattering theory, the forward and backward scattering directions are important for practical engineering problems. That is why, from now onward, we consider these two scattering directions for the rest of the study given in Figs. 5–13. In Fig. 5, the co- and cross-polarized forward and backward SWs as a function of 
$M\eta_{0}$ have been shown for various considered coatings. It should be noted that for this Fig. 5, the numerical values of the considered SWs for 
$M\eta_{0} = 0$ have not been shown. These SW results are also compared with the respective SWs of an uncoated PEMC cylinder having same size as that of coated cylinders. The same cylindrical sizes of uncoated and coated PEMC cylinders are considered to avoid the impact of cylindrical area upon the scattering characteristics. Here we have chosen a relatively shorter wavelength, i.e., 
$\lambda_{0} = 30$ mm with a = 10 mm and b = 20 mm for coated cylinders. Also for an uncoated PEMC cylinder, we have assumed a radius of 20 mm. The relative permittivity and relative permeability of BI, chiral, Tellegen, and strong chiral media are taken to be 2 and unity, respectively. The chirality and Tellegen parameters are same as adopted for Figs. 3 and 4. It is found from Fig. 5 (a, b) that the co- and cross-polarized FSWs of a strong chiral-coated PEMC cylinder is almost independent of the admittance M of the PEMC core. It is studied that the highest value of the co-polarized FSW is observed for a BI-coated PEMC cylinder for a specific value of 
$M\eta_{0} = 0.7$. This highest value is equal to 13.2 dB. The lowest value of the co-polarized FSW is found for a Tellegen-coated PEMC cylindrical object and is equal to 1.43 dB, which occurs for 
$M\eta_{0} = 1.2$. The maximum value of the cross-polarized FSW occur at 
$M\eta_{0} = 2$ for a chiral-coated PEMC cylindrical object. Likewise, the maximum values of cross-polarized FSW for uncoated PEMC and chiral nihility-coated PEMC cylindrical objects occur at 
$M\eta_{0} = \pm 1$. For an uncoated PEMC cylinder, it is found that the minimum value of the co-polarized BSW and the maximum value of the cross-polarized BSW occur at the same value of M, i.e., 
$M\eta_{0} = \pm 1$. This result is in agreement with the Ruppin [Reference Ruppin24]. The maximum value of the cross-polarized BSW is observed for a strong chiral-coated PEMC cylinder, which is equal to 8.655 dB and occurs at 
$M\eta_{0} = -1$. On the other hand, the minimum value of the cross-polarized BSW is found for a chiral-coated PEMC cylinder, which is equal to −34.134 dB and exists for 
$M\eta_{0} = 8$.
Figure 5. The influence of various coatings upon the (a) co-polarized FSW, (b) cross-polarized FSW, (c) co-polarized BSW, and (d) cross-polarized BSW of a PEMC cylindrical object as a function of 
$M\eta_{0}$.
It is well known that the coating thickness is one of the important parameter for scattering analysis from coated cylindrical targets. The influences of coating thickness upon the co- and cross-polarized SWs in the forward and backward directions have been shown in Figs. 6 and 7 for various considered coatings. Here a = 10 mm. For the PEMC core, it is assumed that 
$M\eta_{0} = 1$ and 5. It can be shown that cross-polarized FSW and BSW are almost zero for coated PEC and PMC cylinders with all considered coatings, provided that if coating thickness 
$\Delta = b - a$ is very small, i.e., 
$\Delta = 0.1$ mm. Thus, it is concluded that for very thin layers of BI, chiral, and strong chiral coatings with PEC and PMC core, the cross-polarized FSW and BSW are negligible, which represents the weak nature of birefringence property of these very thin coatings. Contrary to this, for PEMC cylindrical core, there exists non-negligible cross-polarized FSW and BSW for all considered coatings with the coating thickness of 0.1 mm. This is an important result that has not been reported previously, which states that even if the considered coating layers are very thin, the PEMC cylindrical core gives rise to cross-polarized forward and backward scattering. From Fig. 6, it is observed that for a specific thickness of 
$b = 2.26a$, the co-polarized FSW is 12.6 dB and the cross-polarized FSW is −34.4 dB for a BI-coated PEMC cylinder. This is an interesting result, which states that this specific type of BI-coated PEMC cylindrical object can be used to have significant co-polarized forward scattering while suppressing the cross-polarized forward scattering. Such types of enhanced co-polarized forward scattering can be used for point-to-point communication. For a chiral-coated PEMC cylindrical object, there exists a specific thickness of 
$b = 2.22a$, where the co-polarized BSW becomes very small, i.e., −30 dB as compared to the cross-polarized BSW, which is equal to −0.27 dB. Such type of negligible co-polarized backscattering can be used to make the polarization sensitive radar blind and find applications in stealth technology. It is also studied that for a Tellegen-coated PEMC cylinder having coating thickness of 
$b = 2.265a$, the co-polarized BSW is −21.95 dB, which is very small as compared to the corresponding cross-polarized BSW, which is equal to −2.4 dB. This type of Tellegen-coated PEMC cylinder may be used to suppress the co-polarized backscattering. Likewise, for a strong chiral-coated PEMC cylinder with 
$b = 1.91a$, it is found that co-polarized FSW = 12.82 dB and cross-polarized FSW = −32.8 dB. In this case, it is concluded that there exists a significant co-polarized scattering in the forward direction as compared to the respective almost negligible cross-polarized forward scattering. The effects of coating thickness upon the co- and cross-polarized SWs in the forward and backward directions have been shown in Fig. 7 for all the considered coatings for a PEMC core having 
$M\eta_{0} = 5$. For a chiral nihility coating, it is clear from Figs. 6 and 7 that the chiral nihility coating can be used to suppress the cross-polarized scattering in the forward as well as in backward directions, and this suppression seems to be independent of chiral nihility coating thickness. This is because, for a chiral nihility coating, the RCP and LCP wavenumbers, i.e., kr, kl become very small. In this case, kr is on the order of 10−4, whereas kl is on the order of 10−5. This makes the corresponding wavelength associated with an LCP wave very large inside the chiral nihility coating. Therefore, the effective diameter of the coated cylinder seems to be very small for the cross-polarized scattering, which in turn causes negligible cross-polarized scattering. Due to this effect, the strength of the cross-polarized scattered field is weak and almost same for all the considered coating thicknesses and hence independent of coating thickness.
Figure 6. The effects of coating thickness upon the normalized (a) co-polarized FSW, (b) cross-polarized FSW, (c) co-polarized BSW, and (d) cross-polarized BSW of a coated PEMC cylindrical object having various coatings with 
$M\eta_{0} = 1$.
Figure 7. The influence of coating thickness upon the normalized (a) co-polarized FSW, (b) cross-polarized FSW, (c) co-polarized BSW, and (d) cross-polarized BSW of a coated PEMC cylinder with various coatings. Here we have 
$M\eta_{0} = 5$.
It is known that for radar-related problems, only backscattering is important. That is why, in Figs. 8–11, only backscattering widths of co- and cross-polarized components have been shown for Tellegen-, chiral-, and BI-coated PEMC cylinders as functions of admittance M, Tellegen, and chirality parameters. For these coating layers, the fixed values of permittivity 
$\epsilon_{r} = 2$ and permeability 
$\mu_{r}=1$ have been assumed. Here operating wavelength, radii a and b are the same as adopted in Fig. 5. It should be noted that the white regions appearing in Figs. 8–11 represent the values of co- or cross-polarized BSW, which fall below the lowest value of the shown plot legend. For example, in Fig. 8(a), the white regions show the regions where co-polarized BSW falls below −20 dB. The similar arguments exist for white regions appearing in Figs. 8–11. Two important cases are considered here, which are based on Fig. 9(a, b) and Fig. 11(a, b) for a BI-coated PEMC cylindrical rod. For case 1, we have optimal values of 
$M\eta_{0} = 1$, 
$\kappa_{r} = 0.04683$, and 
$\chi_r = 0.5259$ based on Fig. 9(a, b). For these optimal values, we have the co-polarized BSW of −49.8 dB and the cross-polarized BSW of 1.06 dB. In this case, the co-polarized BSW is negligible as compared to the cross-polarized BSW, and this special case may be used to suppress the co-polarized BSW. For case 2, we have optimum parameters of 
$M\eta_{0} = 10$, 
$\kappa_{r} = 0.6726$, and 
$\chi_r = 0.03389$, which are based on Fig. 11(a, b). In this case, we have the co-polarized BSW of 0.068 dB and the cross-polarized BSW of −41.38 dB, which shows that the cross-polarized backscattering may be suppressed. These both cases, i.e., case 1 and case 2, have been shown in Fig. 12. These two cases can be physically explained with the help of Table 1. In Table 1, the comparative study of co- and cross-polarized BSWs of PEMC core cylinder with and without BI coating has been shown. For case 1, it is studied that the cross-polarized BSWs of PEMC cylindrical objects with and without BI coating are almost the same. This shows that in the backward scattering direction, the contribution of the cross-polarized scattered field from this specific BI coating is negligible and that is why the BI coating does not contribute to the overall cross-polarized backscattering from a BI-coated PEMC cylinder. Likewise, for the co-polarized backscattering from a BI-coated cylinder, it is found that an anti-phase co-polarized backscattered field is produced due to the BI coating. Hence, the co-polarized backscattered field from a PEMC cylinder and this anti-phase co-polarized backscattered field cause the overall co-polarized backscattering from a BI-coated cylinder to reduce significantly. For case 2, it can be shown that the cross-polarized backscattered field from this specific BI coating is in anti-phase with respect to the cross-polarized backscattered field of a PEMC cylinder, which in turn causes the overall cross-polarized backscattering to reduce. These two results are interesting and can be used to suppress co- and cross-polarized BSWs, which find applications in radar engineering problems and stealth technology.
Figure 8. (a) Co-polarized BSW and (b) cross-polarized BSW for a Tellegen-coated PEMC cylindrical object as a function of 
$M\eta_{0}$ and χr. (c) Co-polarized BSW and (d) cross-polarized BSW for a chiral-coated PEMC cylindrical object as a function of 
$M\eta_{0}$ and κr.
Figure 9. (a) Co-polarized BSW and (b) cross-polarized BSW of a BI-coated PEMC cylindrical object as a function of κr and χr for 
$M\eta_{0}$ = 1. (c) Co-polarized BSW and (d) cross-polarized BSW of a BI-coated PEMC cylindrical object as a function of κr and χr having 
$M\eta_{0} = -1$.
Figure 10. (a) Co-polarized BSW and (b) cross-polarized BSW of a BI-coated PEMC cylinder as a function of κr and χr for 
$M\eta_{0} = 5$. (c) Co-polarized BSW and (d) cross-polarized BSW of a BI-coated PEMC cylindrical object as a function of κr, χr with 
$M\eta_{0} = -5$.
Figure 11. (a) Co-polarized BSW and (b) cross-polarized BSW of a BI-coated PEMC cylindrical rod for various values of κr, χr and for a fixed value of PEMC admittance, i.e., 
$M\eta_{0} = 10$. (c) Co-polarized BSW and (d) cross-polarized BSW of a BI-coated PEMC cylindrical rod for various values of κr, χr with 
$M\eta_{0} = -10$.
Figure 12. Normalized co- and cross-polarized scattering widths of a BI-coated PEMC cylindrical rod for (a) case 1 and (b) case 2.
Table 1. The comparative study of co- and cross-polarized BSWs for PEMC core with and without BI coating for the considered two cases
The tabulated BSWs have been expressed in dB.
In the previous analysis, we have assumed that the electromagnetic parameters of BI coating is independent of frequency. But, in fact, the BI medium is inherently lossy and has frequency dispersion, see for example [Reference Lindell, Sihvola, Tretyakov and Viitanen2, Reference Grande, Barba, Cabeceira, Represa, Karkkainen and Sihvola40, Reference Awan41]. The frequency dispersive parameters 
$\epsilon_{r}(\omega)$, 
$\mu_{r}(\omega)$, and 
$\kappa_{r}(\omega)$, which are being used in Eqs. (1)–(3), become,
\begin{equation}
\epsilon_{r}(\omega) = \epsilon_{\infty} + \frac{(\epsilon-\epsilon_{\infty})\omega_{0e}^{2}}{\omega_{0e}^{2} - \omega^{2} +j2\Gamma_{e}\omega_{0e}\omega},
\end{equation}
\begin{equation}
\mu_{r}(\omega) = \mu_{\infty} + \frac{(\mu-\mu_{\infty})\omega_{0m}^{2}}{\omega_{0m}^{2} - \omega^{2} +j2\Gamma_{m}\omega_{0m}\omega},
\end{equation}
\begin{equation}
\kappa_{r}(\omega) = \frac{\kappa(\omega)}{\sqrt{\mu_{r}(\omega)\epsilon_{r}(\omega)}},
\end{equation}
\begin{equation}
\kappa(\omega) = \frac{\tau\omega_{0}^{2}\omega}{\omega_{0}^{2} - \omega^{2} + j2\Gamma_{c}\omega_{0}\omega}.
\end{equation} The different parameters appearing in Eqs. (34)–(37) have been adopted from Grande and co-workers [Reference Grande, Barba, Cabeceira, Represa, Karkkainen and Sihvola40], which are given as 
$f_{0} = 3$ GHz, ϵ = 6, 
$\epsilon_{\infty} = 4$, µ = 1.5, 
$\mu_{\infty} = 1.0$, 
$\tau = 15\times 10^{-12}$, 
$\omega_{0e} = \omega_{0m} = \omega_{0} = 2\pi f_{0}$, 
$\Gamma_{e} = \Gamma_{m} = \Gamma = 0.1$. For a Tellegen parameter, it is assumed that χr has a fixed value of 0.7. The influence of frequency dispersive BI coating upon the forward and backward scattering characteristics of a BI-coated PEMC cylindrical object with various values of 
$M\eta_{0}$ has been shown in Fig. 13. One of the important finding with respect to frequency dispersive BI-coated PEMC cylinder has been found for 
$M\eta_{0} = 5$ and at a frequency of f = 6.28 GHz. For this case, it is studied that the co-polarized BSW becomes vanishingly small, i.e., −45 dB as compared to the cross-polarized BSW, which is equal to −1.97 dB. Therefore, it is concluded that this specific type of BI-coated PEMC cylindrical scatterer can be used to suppress the co-polarized scattering in the backward direction at the specific frequency. It is already mentioned that such type of negligible co-polarized backscattering can be used to make the polarization-sensitive radar blind and find applications in stealth technology.
Figure 13. (a) Co-polarized FSW, (b) cross-polarized FSW, (c) co-polarized BSW, and (d) cross-polarized BSW of the frequency dispersive BI-coated cylindrical object having various core materials.
Conclusions
The scattering characteristics of a BI-coated PEMC cylindrical object has been investigated. Using an idea of CVWFs along with the application of tangential boundary conditions, the proposed problem has been solved. The scattering coefficients have been derived in their simplest forms. To verify the correctness of the analytical formulation and the numerical code, the numerical results have been compared with the previous published work using some special cases. It is studied that by varying the admittance of PEMC material, chirality, Tellegen parameter, and coating thickness, one can optimize the scattering characteristics for a specific application. During the study, it is found that the chiral nihility coating can be used to suppress the cross-polarized scattering characteristics of a PEMC cylindrical object. It is also studied that the specific types of BI-coated and strong chiral-coated PEMC cylindrical objects having certain coating thicknesses can be used to suppress the cross-polarized forward scattering while enhancing the co-polarized forward scattering significantly. This is an interesting result, and such types of enhanced co-polarized forward scattering can be used for point-to-point communication. Two special cases are discussed for a BI-coated PEMC cylindrical object where the co-polarized and the cross-polarized backscattering may be suppressed, which find applications in radar engineering problems and stealth technology. Finally, the influence of frequency dispersive BI coating has been discussed.
Funding statement
This research received no specific grant from any funding agency, commercial, or not-for-profit sectors.
Competing interests
The authors report no conflict of interest.
Zeeshan Akbar Awan received the Master of Philosophy from Department of Electronics, Quaid-i-Azam University, Islamabad, Pakistan, in 2002. He has completed his Ph.D. degree in Electronics from the same university. He has worked as a post-doctoral candidate within LEOST Laboratory of the COSYS Department in IFSTTAR, Lille, France, from January to July 2018. He is presently an associate professor at the Department of Electronics, Quaid-i-Azam University, Islamabad, Pakistan. He has authored or co-authored more than 40 research articles. His research interests include electromagnetic scattering, metamaterials, metasurfaces, and antenna theory.
Abdul Raqeeb received his Master degree in Physics from Bahauddin Zakariya University, Multan, Pakistan, in 2021. He has also received his Master of Philosophy degree in Electronics from the Quaid-i-Azam University, Islamabad, Pakistan, in 2023. His main areas of research include electromagnetic scattering and metamaterials.
Arshad Hussain received the M.Phil from Department of Electronics, Quaid-i-Azam University, Islamabad, Pakistan, in 2002. He completed his Ph.D. from State Key Laboratory of Analog and Mixed-Signal VLSI, Department of Electrical and Computer Engineering, Faculty of Science and Technology, University of Macau, Macau (SAR), China. He also completed 1-year Post-Doctorate from Department of Information and Communication Engineering, Chosun University, GwangJu, South Korea. He is currently working as Assistant Professor at the Department of Electronics, Quaid-i-Azam University, Islamabad, Pakistan. His current research interests are analog circuits, switched-capacitor circuits, design of low-power high-resolution delta-sigma ADCs and electromagnetics.
