Published online by Cambridge University Press: 05 October 2023
A wideband antipodal Vivaldi antenna has been designed and optimized. A slight improvement is obtained by employing multiple metalense based on circular split-ring resonators to maximize the antenna gain with the maximum bandwidth. The designed antennas have been fabricated and characterized, showing good agreement with simulations. The maximum measured gain is 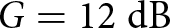 $G = 12\;{\textrm{dB}}$, and the −10 dB bandwidth is from
$G = 12\;{\textrm{dB}}$, and the −10 dB bandwidth is from 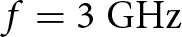 $f = 3\;{\textrm{GHz}}$ to
$f = 3\;{\textrm{GHz}}$ to 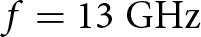 $f = 13\;{\textrm{GHz}}$.
$f = 13\;{\textrm{GHz}}$.