Introduction
During the last decade, we have witnessed the increasing development of millimeter-wave systems for focusing electromagnetic energy in the near field [Reference Fuscaldo1,Reference Martinez-Ros2]. Indeed, diffraction and dispersion are well-recognized physical phenomena that limit the performance of millimeter-wave radiators. However, modern microwave and millimeter-wave applications, such as wireless power transfer, radiometry, thermal ablation, and so on, have pushed researchers to find solutions that exhibit either limited-diffractive or limited-dispersive features. Well-known examples of such solutions are Bessel beams and, more recently, X-waves (XWs) [Reference Hernández-Figueroa, Zamboni-Rached and Recami3,Reference Hernández-Figueroa, Zamboni-Rached and Recami4].
As is known [Reference Hernández-Figueroa, Zamboni-Rached and Recami3], both solutions, viz., Bessel beams and XWs, can be interpreted as the monochromatic (beams) and the polychromatic (pulses) versions, respectively, of the more general class of nondiffracting waves. Despite the interest in these solutions dates back to the end of the 80s and the beginning of the 90s, when the first experimental realizations appeared in optics [Reference Saari and Reivelt5] and acoustics [Reference Lu and Greenleaf6], there are still only a few implementations in the microwave regime (see, e.g., [Reference Fuscaldo7] and Refs. therein). Just very recently, theoretical and numerical results have been reported in [Reference Fuscaldo7–Reference Pavone9], whereas experimental results just appeared in [Reference Chiotellis10].
Indeed, most of the microwave Bessel-beam launchers were initially based on a scalar design approach [Reference Li11], as is typical in optics where the paraxial approximation holds. As a consequence, the beams generated by such devices are characterized by relatively large spot-sizes at the expense of a rather poor resolution. In this connection, it has been shown that leaky waves (LWs) can profitably be used for generating Bessel beams with considerably narrower spot-sizes in both microwave [Reference Ettorre and Grbic12,Reference Ettorre, Rudolph and Grbic13] and millimeter-wave ranges [Reference Fuscaldo1]. However, both these leaky-wave antennas (LWAs) exhibit a narrow operating fractional bandwidth, and thus they are not suitable for the generation of polychromatic nondiffracting waves, such as XWs [Reference Fuscaldo7]. This narrow-band feature is due to the resonant character of the radiation mechanism, which is typically based on the superposition of an outward and an inward cylindrical wave [Reference Chávez-Cerda14].
Nevertheless, it has recently been shown that Bessel beams can conveniently be generated using inward cylindrical waves only [Reference Albani15–Reference Comite17], thus leading to the design of wideband radiators. (Note that in [Reference Albani15] analytical results are obtained for zeroth-order Bessel beams, whereas in [Reference Comite17] numerical results are extended to higher orders.) Even more interestingly, in [Reference Cai18] this principle has been successfully used to design a sinusoidally-modulated LWA based on the excitation of a backward leaky wave. However, in that work, neither the impact of the attenuation constant, nor a rigorous dispersion analysis has been provided. Furthermore, the wideband potential of using backward LWs has not yet been discussed in connection with the possibility of generating XWs.
In this work, we propose an azimuthally-invariant periodic LW radiator, namely a parallel-plate radial waveguide with annular slots (see Fig. 1) [Reference Podilchak19,Reference Podilchak20], suitably designed for the generation of Bessel beams and XWs at millimeter waves (around 60 GHz). A rigorous dispersion analysis is carried out in order to ensure limited-dispersion properties over a considerable fractional bandwidth (20%). The impact of the attenuation constant on the focusing capabilities of backward LWs is first evaluated on a theoretical basis. On this ground, the geometrical parameters of the structure are selected in order to meet the design requirements. Finally, numerical results confirm the promising capabilities of the proposed device for the generation of limited-diffractive leaky waves. Specifically, focusing pulses are generated by spectral superposition of Bessel beams over the entire theoretical bandwidth. A comparison is then performed between pulses generated with either a uniform frequency spectrum or a Gaussian one.
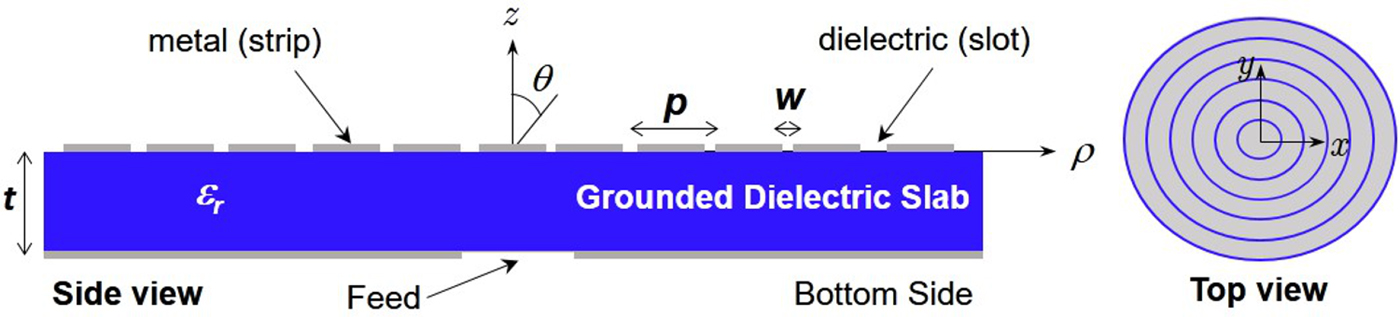
Fig. 1. Side and top views of the proposed azimuthally-invariant periodic leaky-wave antenna (LWA) for near-field focusing. Parameters in the text.
The paper is organized as follows. In the section “Theoretical analysis”, we envisage the theoretical aspects related to the generation of nondiffracting waves through both inward cylindrical waves (section “Generation of nondiffracting waves through inward cylindrical waves”) and backward LWs (section “Generation of nondiffracting waves through backward leaky waves”); a preliminary design of a periodic LWA is proposed in the section “Design of a periodic LWA”. In the section “Generation of limited-diffractive beams and limited-dispersive XWs through an LWA”, the performance of the LWA design outlined in the section “Design of a periodic LWA” is extensively discussed in connection with the generation of nondiffracting beams (section “Generation of Bessel beams through an LWA”) and nondiffracting pulses (section “Generation of XWs through an LWA”). Finally, conclusions are drawn in the section “Conclusion”.
Theoretical analysis
Generation of nondiffracting waves through inward cylindrical waves
As is known [Reference Hernández-Figueroa, Zamboni-Rached and Recami3,Reference Fuscaldo7], an ideal XW can be generated by taking the inverse Fourier transform of monochromatic zeroth-order Bessel beams
$$ \chi(\rho,z;t) = \int_{-\infty}^{+\infty}W(\,f)J_0(k_{\rho}\rho)e^{-jk_zz}e^{\,j2\pi f t}df, $$where J 0( · ) is the zeroth-order Bessel function of the first kind, t is the time, f the frequency, and W(f) is a spectral weighting function; ρ and z are the radial and longitudinal coordinates of a cylindrical reference frame (see Fig. 1), and k ρ and k z the radial and longitudinal wavenumbers, respectively, related through the separation relation 
${k_0^2=k_\rho ^2+k_z^2}$, k 0 being the vacuum wavenumber. According to the definitions provided in [Reference Hernández-Figueroa, Zamboni-Rached and Recami3,Reference Hernández-Figueroa, Zamboni-Rached and Recami4], ordinary XWs are weighted with an exponentially-decaying frequency spectrum [Reference Hernández-Figueroa, Zamboni-Rached and Recami3]. In this work, we will refer to two different kinds of spectral weights: uniform (UXWs) [Reference Fuscaldo7] and Gaussian (GXWs) [Reference Pavone9].
From equation (1) it is clearly seen that XWs are nothing more than a weighted spectral superposition of Bessel beams. As a consequence, any radiating device which is able to efficiently generate Bessel beams over a certain frequency bandwidth is a potential candidate for generating XWs (some restrictions will be discussed in the section “Generation of limited-diffractive beams and limited-dispersive XWs through an LWA”).
More generally, the vectorial formulation of Maxwell's equations in a cylindrical reference frame shows that a cylindrical aperture of infinite extent supports the generation of Bessel beams in the near-field region. Indeed, if we suppose to excite the structure with an azimuthally-symmetric source (e.g., a vertical coaxial feed), the electromagnetic field can completely be described by considering a transverse magnetic (with respect to the vertical z-axis) TMz vector potential 
$A_z=H_0^{(2)}(k_\rho \rho )e^{-jk_zz}$ [Reference Ip and Jackson21], which gives rise to the following electric field components [Reference Harrington22]
$$ E_z(\rho,z)\propto H^{(2)}_0(k_{\rho}\rho)e^{-jk_z z}, $$
$$ E_{\rho}(\rho,z) \propto H^{(2)}_1(k_{\rho}\rho)e^{-jk_z z}, $$
$$ E_{\phi}(\rho,z) = 0, $$where 
$H_0^{(2)}(\cdot )$ and 
$H_1^{(2)}(\cdot )$ are the outward Hankel functions of order 0 and 1, respectively. We note that the assumption of infinite extent (which also holds for electrically large apertures provided that the field is sufficiently attenuated at the edge truncation, as customarily happens for LWAs [Reference Jackson, Oliner and Balanis23,Reference Galli, Baccarelli, Burghignoli and Webster24]) allows for retaining only the outward components of a cylindrical wave (generally constituted by a superposition of outward and inward Hankel waves).
Since an inward cylindrical-wave aperture distribution is needed to focus a Bessel beam [Reference Albani15], and inward and outward Hankel functions are related through [Reference Abramowitz and Stegun25]
$$ H_n^{(1)}(k_\rho\rho)=-H_n^{(2)}(-k_\rho\rho), $$for n ∈ ℤ, then equations (2) and (3) evaluated at z=0 reveal that k ρ must be negative to recover the inward character of the aperture distribution, and in turn be able to generate Bessel beams. This principle has been profitably applied in [Reference Cai18] to backward LWs, for which k ρ = β ρ − jα ρ with phase constant 
$-k_0\leq \ \beta_\rho \leq 0$ and attenuation constant (or leakage rate) α ρ > 0.
Generation of nondiffracting waves through backward LWs
The analysis reported in [Reference Albani15] was derived under the assumption that k ρ ∈ ℝ. In fact, for α ρ = 0, geometrical optics [Reference Albani15,Reference Durnin26] predicts a Bessel beam in a diamond-shaped region delimited by the shadow boundaries (see white dashed lines in Figs 2(a)–2(d)) at an angle θ 0 called axicon angle (measured from the vertical z-axis) related to the wavenumbers through [Reference Durnin26]
$$ \tan\theta_0=k_\rho/k_z. $$This simple geometrical interpretation also allows for calculating the so-called nondiffracting range, i.e., the distance z = z ndr from the aperture plane z=0 at which the shadow boundaries intersect each others, and thus the beam intensity abruptly decays (the beam enters the shadow region), through the relation
$$ z_{{ndr}}=\rho_{{ap}} / \tan \theta_0, $$where ρ ap is the aperture radius.
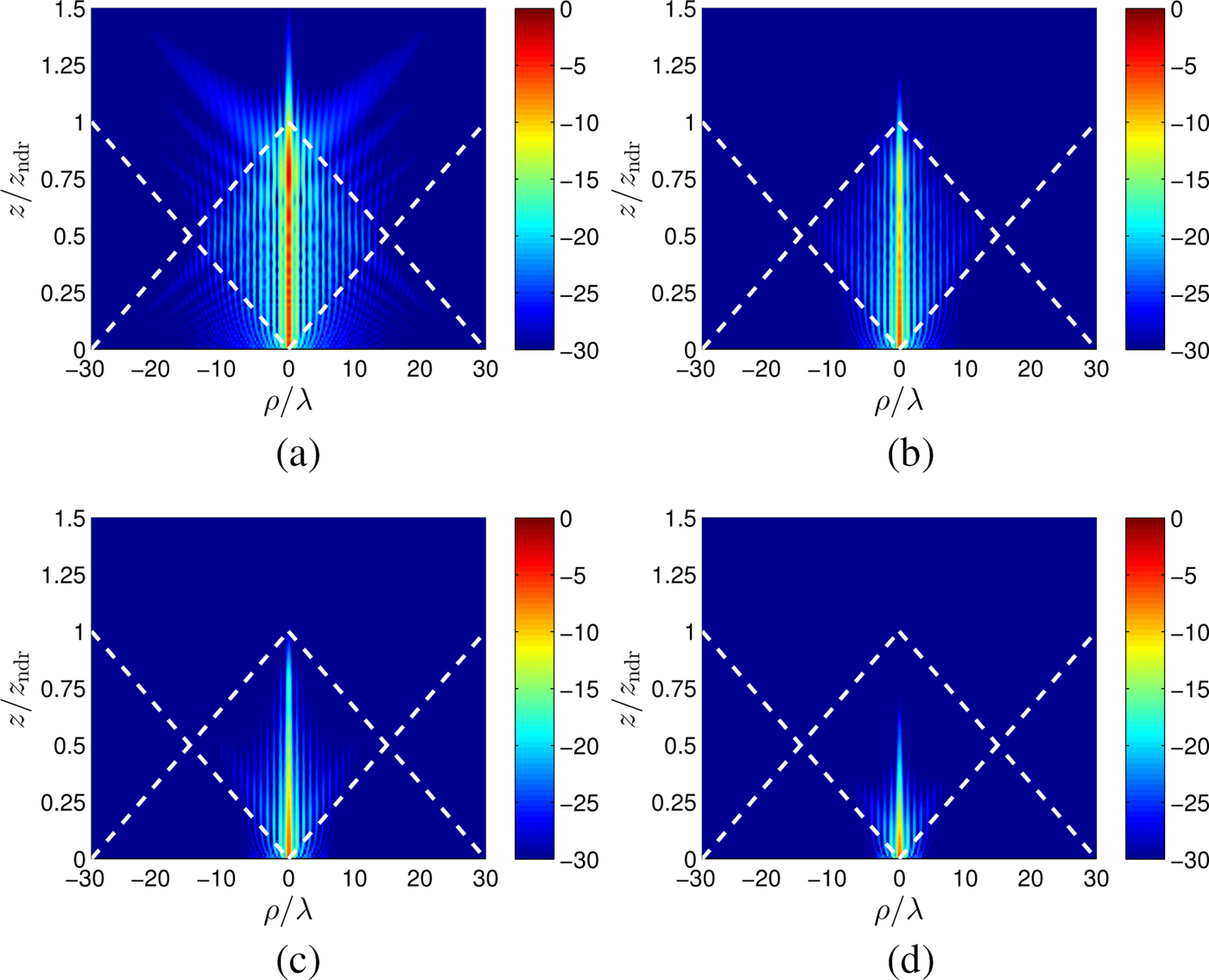
Fig. 2. Color maps of the normalized absolute value (in dB) of the E z component of the electric field at 60 GHz along an arbitrary ρz plane limited by |ρ| < 30λ and 0 < z < 1.5z ndr, for β ρ = −0.5k 0 and (a) α ρ = 0, (b) α ρ = 0.005k 0, (c) α ρ = 0.01k 0, and (d) α ρ = 0.02k 0. In all cases, a zeroth-order Bessel-like beam is clearly distinguishable within the diamond-shaped region defined by the shadow boundaries (white dashed lines).
To extend such analysis to LW radiators we need to evaluate the impact of the attenuation constant on the Bessel-beam generation, a leaky mode being characterized by a radial complex wavenumber k ρ = β ρ − jα ρ. As stated in [Reference Cai18], it is expected that the exponential decay of LWs (described by their attenuation constant) would produce Bessel beams over a smaller spatial region.
To give a proof of concept, in Figs 2(a)–2(d) the absolute value of the E z component is reported in dB for a Bessel beam generated by a finite aperture with radius ρ ap = 30λ at 60 GHz (being λ = 0.5 cm the free-space wavelength), assuming a backward leaky wave characterized by a normalized phase constant 
$\hat {\beta }_{\rho }=\beta_{\rho } / k_0=-0.5$ (corresponding to an axicon angle θ 0 = 30° through equation (6)) and considering four different values of the normalized attenuation constant 
$\hat {\alpha }_{\rho }=\alpha_{\rho }/k_0$, ranging from 0 to 0.02. Results have been obtained by numerically evaluating the radiation integral [Reference Fuscaldo7] using the aperture field distribution given by the non-zero tangential components of the electric field (viz., E ρ in equation (3)) at the aperture plane z=0. Since 
$-1<\hat {\beta }_{\rho }<0$ due to the backward nature of the leaky mode, E ρ is equivalently described by an inward Hankel distribution 
$H_1^{(1)}(\cdot )$ with a positive argument (see equation (5) for n=0), as required to focus a Bessel-like beam within the nondiffractive range [Reference Albani15].
As is seen, when 
$\hat {\alpha }_{\rho }=0$ (see Fig. 2(a)), a zeroth-order Bessel beam is efficiently generated in a diamond-shaped region, which is determined by the corresponding shadow boundaries (white dashed lines) [Reference Albani15,Reference Ettorre16]. However, when 
$\hat {\alpha }_{\rho }$ increases [see Figs 2(b)–2(d)], the electric field exhibits an exponential decay, which limits the intensity of the field more and more as long as the leakage rate 
$\hat {\alpha }_{\rho }$ increases. This is in agreement with the experimental results recently reported in [Reference Cai18]. On one hand, it is seen that for small leakage rates, i.e., 
$\hat {\alpha }_{\rho }\leq 0.01$ (see Figs 2(b) and 2(c)), the impact of 
$\hat {\alpha }_{\rho }$ is even beneficial to ‘smooth’ the beam from the diffractive behavior of the field outside the diamond-shaped region (see Fig. 2(a)). On the other hand, for higher leakage rates, i.e., 
$\hat {\alpha }_{\rho }\geq 0.02$ (see Fig. 2(d)), the impact of 
$\hat {\alpha }_{\rho }$ has a detrimental effect, leading to a vanishing Bessel beam. As a consequence, in order to design an LWA for efficiently generating Bessel beams (and in turn XWs), the 
$\hat {\alpha }_{\rho }$ should preferably never be higher than 0.02.
It is worth mentioning that the value of 
$\hat {\alpha }_{\rho }$ has in practice also a lower bound. Indeed, in order to let an LWA radiate the 90% of its power (this also guarantees that the numerical results would not differ much from the theoretical formulation underlying equations (2)-(3), which is based on the infinite-aperture assumption), the aperture radius is determined by the following design rule [Reference Jackson, Oliner and Balanis23]:
$$ \rho_{{ap}}\simeq 0.18\lambda / \hat{\alpha}_{\rho}. $$ A very small value of 
$\hat {\alpha }_\rho$ would produce impractically large apertures in terms of wavelengths, especially at microwaves. (Note that, in the example of Fig. 2, ρ ap has been fixed to 30λ to approximately fulfill the aforementioned design rule for the smallest considered leakage rate, viz., 
$\hat {\alpha }_{\rho }=0.005$.)
Design of a periodic LWA
These considerations have been used to design an annular strip-grating ‘bull-eye’ LWA, i.e., a parallel-plate radial waveguide (PPW) with annular slots (see Fig. 1) which can support a backward cylindrical LW [Reference Jackson, Oliner and Balanis23]. This structure can easily be fed by a printed surface-wave launcher by coupling a coplanar waveguide feedline to a slot etched in the ground plane [Reference Podilchak19], or by a coaxial feed [Reference Baccarelli27], if azimuthally symmetric fields are required.
When the size of the annular slots w is small with respect to the period p (see Fig. 1), the n=0 Floquet harmonic can be seen as a perturbation of the transmission electron microscopy (TEM) mode of the unperturbed PPW. As a consequence, the wavenumber of the radiating n=−1 Floquet harmonic is approximately given by 
${k_{\rho ,-1}(f)=\beta ^{{TEM}}_{\rho } +\Delta \beta_{\rho }-j\alpha_{\rho }-2\pi /p}$, where Δβ ρ is the perturbation of the phase constant, α ρ is the attenuation constant due to the presence of the slots, and 
${\beta ^{{TEM}}_{\rho }=k_0\sqrt {\varepsilon_{\rm {r}}}}$ is the wavenumber of the TEM mode supported by the unperturbed PPW filled by a dielectric with permittivity ε r.
Once the frequency is fixed, 
$\beta_{\rho }^{{TEM}}$ depends only on ε r. Assuming small perturbations, even β ρ,−1 depends only on ε r. As a consequence, once the minimum and maximum values of 
$\beta_{\rho ,-1}=\Re \{k_{\rho ,-1}\}$ at the edges of the bandwidth [i.e., β ρ,−1(f min) and β ρ,−1(f max)] are fixed, the fractional bandwidth (defined as Δf = (f max − f min)/f op) depends only on the slope of β ρ,−1, which is solely determined by ε r. In particular, here we fixed β ρ,−1 to take values within the range − 0.4k 0 ≤ β ρ,−1 ≤ −0.1k 0 over a fractional bandwidth of 20% centered around f op = 60 GHz (viz., a 54–66 GHz bandwidth). Such constraints give us ε r = 1.2 and p=3.716 mm, whereas the width of the slots has been preliminarily set to w=0.416 mm in order to get a ‘moderate’ leakage rate. The thickness of the substrate has been set to t=0.83 mm (t ≃ λ/6) to prevent the propagation of higher-order modes. With these values at hand, the dispersion curve of this structure has been obtained by means of a method-of-moments (MoM) in-house code (see, e.g., [Reference Baccarelli28]).
As is shown in Figs 3(a) and 3(b), the phase constant is limited in the range − 0.47k 0 < β ρ,−1 < −0.18k 0 over the entire bandwidth, whereas the attenuation constant is remarkably regular around the value of α ρ ≃ 0.005k 0; such a value fixes the aperture size to ρ ap = 40λ = 20 cm through equation (8).
Fig. 3. (a) Normalized phase β ρ,−1/k 0 and (b) attenuation α ρ/k 0 constants versus f, for the proposed LWA. The dispersion curves have been obtained through a method-of-moments (MoM) in-house code [Reference Baccarelli28].
In the following section “Generation of limited-diffractive beams and limited-dispersive XWs through an LWA”, we will use the dispersion values given by the MoM code to assess the generation of limited-diffractive Bessel beams and limited-dispersive pulses through the proposed annular strip-grating LWA.
Generation of limited-diffractive beams and limited-dispersive XWs through an LWA
Generation of Bessel beams through an LWA
To have an ideal XW, k ρ and k z appearing in equation (1) should change linearly with frequency, whereas in any microwave radiating device (as those considered here) they generally exhibit a nonlinear behavior, thus causing the well-known frequency dispersion of the wavenumber. Since the ratio between k ρ and k z defines the axicon angle θ 0 through equation (6), the frequency dispersion of the wavenumber is also referred to as cone dispersion [Reference Porras, Valiulis and Di Trapani29] to emphasize the variation of θ 0 with the frequency. This aspect is particularly important for practical realization of XWs, as we will see in the next section “Generation of XWs through an LWA”.
According to the dispersion curves of the proposed ‘bull-eye’ LWA (see Fig. 3(a)), the axicon angle is expected to change within the range 10° < θ 0 < 30° (through equation (6)) over the considered bandwidth (i.e., for f min ≤ f ≤ f max with f min = 54 GHz and f max = 66 GHz). As a consequence, the nondiffractive range z ndr(f) attains the following values: z ndr(f min) ≃ 37 cm, z ndr(f op) = 60 cm, and z ndr(f max) = 108 cm, at 54 GHz, 60 GHz, and 66 GHz, respectively. Numerical results for E z (see Figs 4(a)–4(c)) corroborate the theoretical prediction.
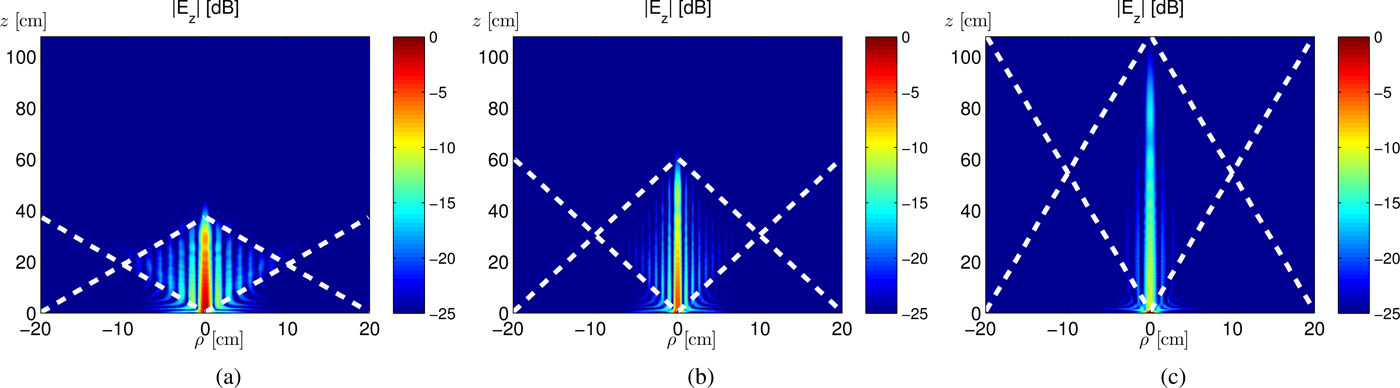
Fig. 4. Color maps of the normalized absolute value (in dB) of the E z component of the electric field at (a) f=54 GHz, (b) f=60 GHz, and (c) f=66 GHz, along an arbitrary ρz plane limited by |ρ| < ρ ap and 0 < z < z ndr(f max). Due to the unavoidably dispersive character of the backward leaky wave, the shadow boundaries (white dashed lines) change as f and hence β ρ,−1 changes.
As is clearly seen, the shadow boundaries (white dashed lines) stretch out as the frequency increases according to the dispersion relation of β ρ,−1. It also manifests that the intensity distribution of E z resembles that of a Bessel beam characterized by an attenuation constant of the order of α ρ = 0.005k 0, previously evaluated (compare Fig. 4(b) with Fig. 2(b)). Even more interestingly, the Bessel-beam profile is maintained over the whole frequency range of interest (results for intermediate frequencies are similar), thus opening to the possibility of generating polychromatic nondiffracting waves such as XWs, as continuous frequency superpositions of nondiffracting beams such as Bessel beams. This fundamental issue is addressed next.
Generation of XWs through an LWA
Since in the previous section “Generation of Bessel beams through an LWA” we have seen that the considered LWA allows us for generating Bessel-like beams for the longitudinal component of the electric field over the entire frequency range, it is expected that the same structure would also be able to generate a focusing propagating pulse closely similar to an XW.
In fact, it has recently been established [Reference Fuscaldo7] that the efficient generation of UXWs through finite apertures at microwaves is subjected to the fulfillment of specific criteria regarding the bandwidth capabilities, the aperture size, and the frequency dispersion of the device.
These considerations originally suggested the use of radial line slot array (RLSA) antennas for generating both UXWs and GXWs [Reference Fuscaldo7,Reference Pavone9], but the discussion is still valid for any mm-wave radiator, provided that the mechanism of radiation is described by a single propagating mode characterized by a real wavenumber, i.e., α ρ = 0. However, we have extensively shown in the previous Subsections that the only effect of the imaginary part of the leaky wavenumber is to produce a decay of the beam intensity for 0 ≤ z ≤ z ndr. Since Bessel beams are the main constituents of XWs it is expected that an XW generated by means of backward LWs will exhibit a similar behavior along the propagating z-axis.
Here, we aim at showing that the LWA design outlined in the section “Design of a periodic LWA” also fulfills the criteria established in [Reference Fuscaldo7] to efficiently generate UXWs. In fact, according to [Reference Fuscaldo7], the confinement ratios along the radial C ρ and the longitudinal C z axes (defined as the ratios between the − 3 dB widths of the main spot along the respective ρ, z directions) and the maximum nondiffracting extensions (i.e., 2ρ ap along the radial axis, and z ndr along the longitudinal axis) are given by the following two exact analytic expressions:
$$C_\rho = {\,j_{0,1} \over \pi\sin\theta_0\rho_{{ap}} / \lambda}, $$
$$C_z = {2\sin\theta_0 \over {\Delta f}\cos^2 \theta_0\, \rho_{{ap}}/\lambda}, $$where j 0,1 ≃ 2.405 is the first zero of J 0( · ), and Δf is the fractional bandwidth. Through equations (9) and (10), it is easily seen that, when Δf = 20% and ρ ap = 40λ = 20 cm, a good confinement of the pulse along both the transverse and the longitudinal axes (i.e., both C z ≪ 1 and C ρ ≪ 1) is obtained for axicon angles within the range 5° ≤ θ 0 ≤ 30°. Such a cone dispersion is larger than that exhibited in Fig. 3(a) (viz., 10° ≤ θ 0 ≤ 30°), thus confirming the consistency of the proposed LWA design.
It should be stressed that equations (9) and (10) are exact only in the nondispersive case, i.e., θ 0(f) = θ 0, but they still work as lower-bounds for the dispersive case. In general, the minimization of the cone dispersion is highly desirable since it determines the frequency-dependent character of z ndr [through equation (7)], which is responsible of the spatio-temporal spreading of XWs: the higher the dispersion, the faster the pulse will broaden as it propagates [Reference Fuscaldo7,Reference Comite8].
To further verify our design, numerical results have been obtained by replacing the ideal Bessel beams appearing in equation (1) with the longitudinal component of the electric field E z effectively radiated by the LWA over the considered frequency range. This has led to the following expression:
$${\cal E}_z(\rho,z;t) = \int_{-\infty}^{+\infty}W(\,f)E_z(\,f)e^{\,j2\pi f t}df. $$ Since we were interested in propagating the pulse over a distance 
${z=z_{{ndr}}(f_{{max}})}=108\rm cm$, and the longitudinal group velocity v z of the pulse is approximately equal to v z = 0.696c 0 (c 0 being the speed of light in vacuum), the pulse has been observed over a period T=5 ns. To avoid fictitious replicas for 0 ≤ t ≤ T due to aliasing we have then numerically evaluated the integral of equation (10) using 
${N_f>\lceil f_0\Delta fT\rceil =60}$ frequency samples (where 
$\lceil x \rceil$ returns the smallest integer ≥ x), according to the Nyquist-Shannon theorem.
Two cases of interests are then examined: (i) the generation of UXWs, i.e., XWs weighted with a uniform frequency spectrum:
$$W(\,f)= \left\{\matrix{ 1 \hfill & f_{{min}} \lt f \leq f_{{max}}, \cr 0 \hfill & {\rm elsewhere} \hfill} \right. $$and (ii) generation of GXWs, i.e., XWs weighted with a Gaussian frequency spectrum:
$$W(\,f)=\sqrt{{1 \over \sigma_{{\,f}}\sqrt{\pi}}}e^{-({(\,f-f_0)^2}/{2\sigma_{{\,f}}^2)}}, $$where σ f can be related to the frequency bandwidth through the following relation
$$\sigma_{\rm f} = {\,f_{{max}}-f_{{min}} \over 2\sqrt{\ln1/s}}, $$where s is an arbitrary threshold parameter which depends on the bandwidth definition (e.g., the standard choice of − 10 dB bandwidth made in Fig. 5 is given by s=0.1). Note that the amplitude factor in front of the exponential function in equation (13) is needed to have a normalized power spectrum, i.e., |W(f)|2 = 1.
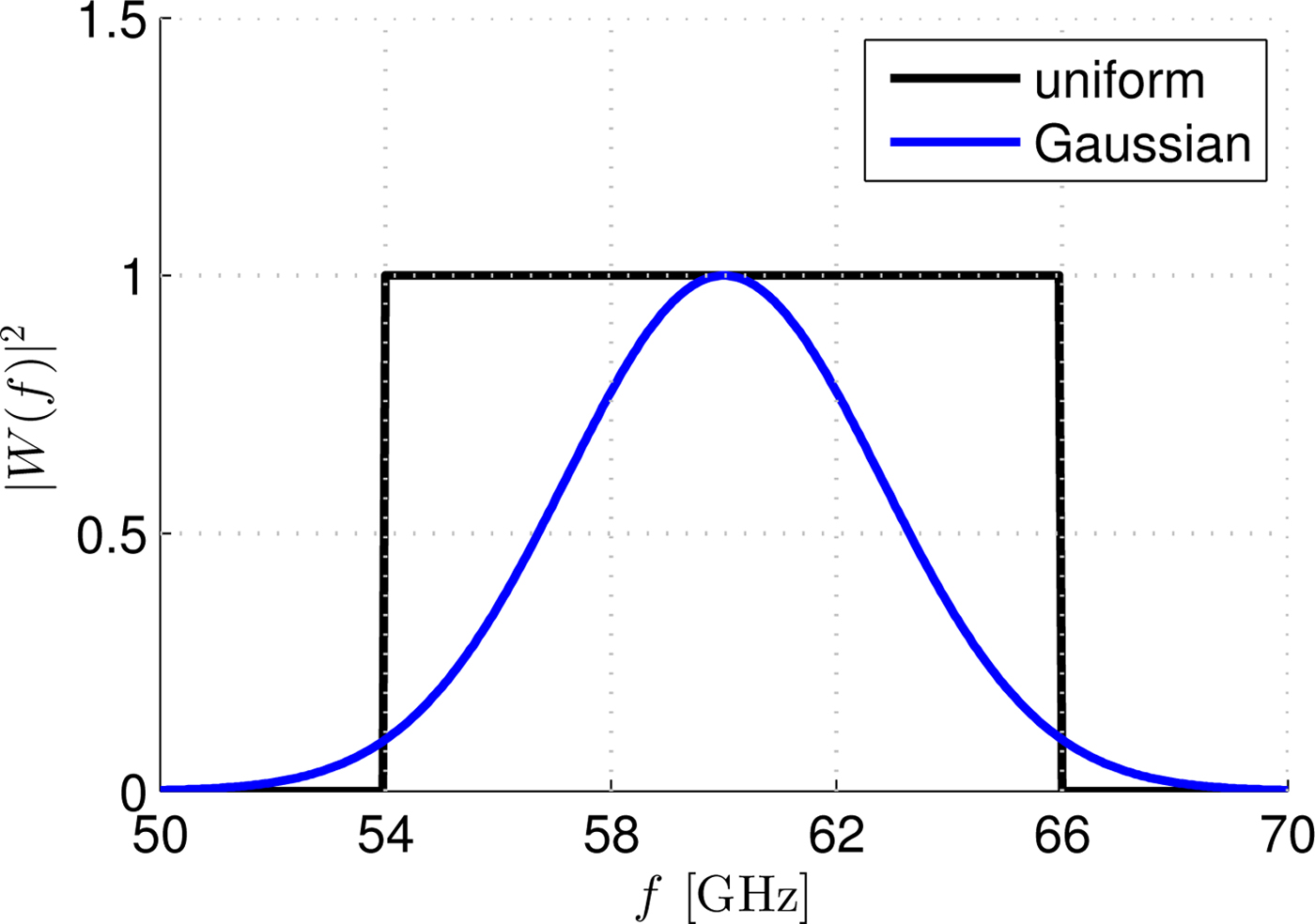
Fig. 5. Normalized frequency power spectra |W(f)|2 for a uniform weight (black solid line) and a Gaussian weight (blue solid line) with s=0.1.
We chose these two kinds of frequency spectra for a two-fold reason. On one hand, uniform frequency spectra, even if they cannot constitute a ‘true’ signal due to their finite spectral extent, are more amenable for validating results provided by a frequency-domain measurement campaign. As a matter of fact, any experimental validation based on measurements of the frequency components in the near field can be performed only over a band-limited frequency spectrum. On the other hand, Gaussian frequency spectrum (which of course can represent a true signal) is the most employed frequency spectrum for characterizing the reference pulses in time-domain measurements based on autocorrelation techniques and optical gating [Reference Bowlan30,Reference Trebino31].
The resulting focusing LW pulses have been reported in Figs 6(a)–6(c) for UXWs and in Figs 6(d)–6(f) for GXWs. In both sets of figures the intensity distribution of 
${\cal E}_z(\rho ,\,z;t)$ has been captured at three different time instants to illustrate the movement of the pulse from z < z ndr(f min) to z > z ndr(f op) (z ndr(f max) corresponds to the upper-limit of the vertical axis). As is seen, the main spot exhibits the peculiar ‘X-shape’ that characterizes all types of XWs. Furthermore, as long as the pulse is in z < z ndr(f min) the intensity of the maximum as well as the spot size are not strongly perturbed. However, as the pulse travels beyond z ndr(f min), the shape of the main spot is progressively distorted and the intensity starts to fade out; beyond z ndr(f op) the intensity of the pulse abruptly decays and the main spot is barely appreciable.
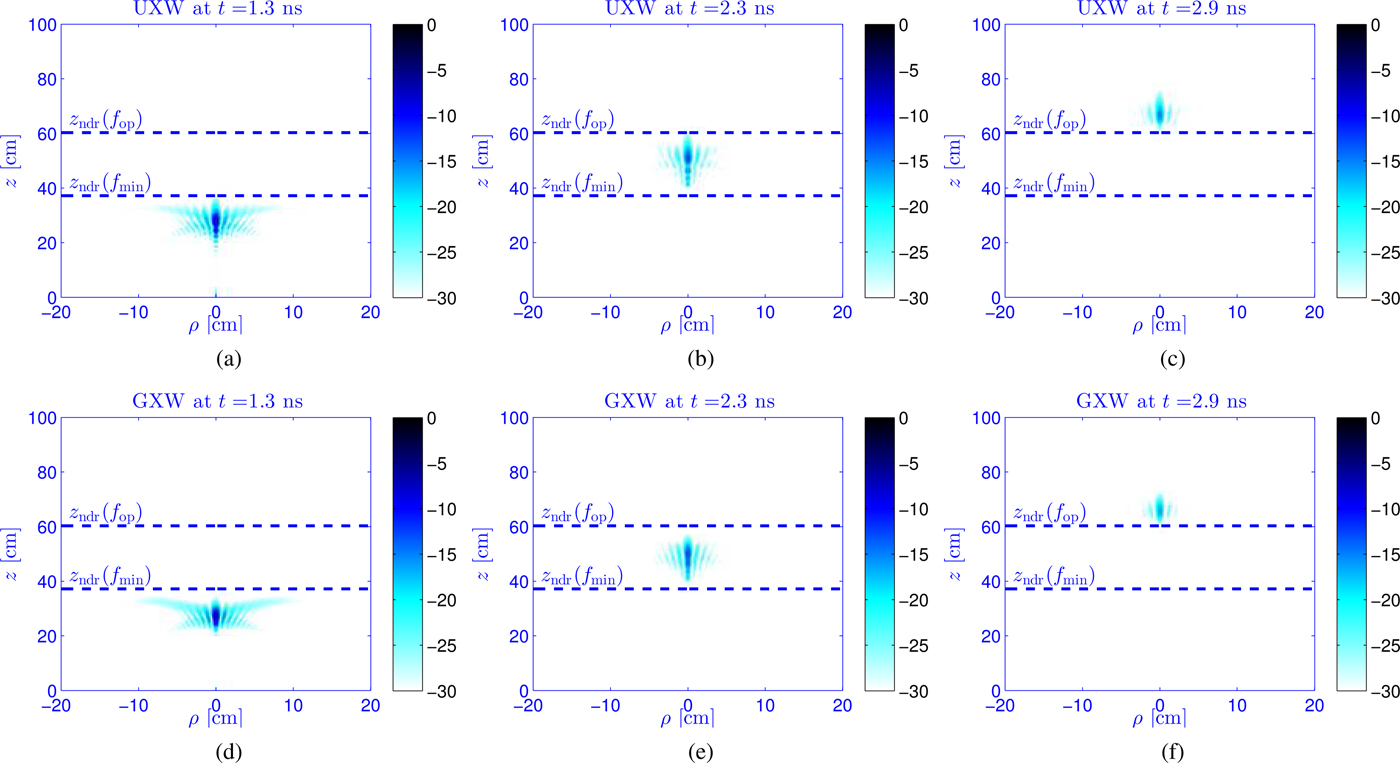
Fig. 6. Time evolution of (a)-(c) UXWs and (d)-(f) GXWS generated by means of focusing leaky waves. The intensity of 
${\cal E}_z(\rho ,\,z;t)$ has been captured at (a) and (d) t=1.3 ns, (b) and (e) t=2.3 ns, (c) and (f) t=2.9 ns, to show the distortion and the decay of the main spot of the pulse before and beyond the minimum and the operating nondiffractive ranges.
Differences between UXWs and GXWs are hardly noticeable because the main features of the pulse come from the spectral content close to the operating frequency [Reference Fuscaldo7] where the Gaussian power spectrum is maximum (see Fig. 5). However, a closer look reveals that the GXW has a slightly larger − 3 dB spot-width along the longitudinal axis and exhibits a slightly lower dispersive behavior. These two facts are both in agreement with equation (10) since a Gaussian weight would reduce the ‘effective’ fractional bandwidth of the pulse, thus increasing C z and in turn worsening the confinement along the z-axis. Moreover, the dispersion effects are less important over a reduced fractional bandwidth, thus determining the weaker dispersion of GXWs with respect to UXWs.
As a final comment, we should stress that our results are very similar to those experimentally obtained at microwaves with a broadband Bessel beam radiator [Reference Chiotellis10]. Differently from [Reference Chiotellis10], the XWs reported here exhibit a gradual broadening and decay of the energy as long as the pulse overcomes the theoretically predicted nondiffractive range. Furthermore, we should remark that XWs reported here are of subluminal type, as opposed to the superluminal ones reported in [Reference Chiotellis10]. Such different behaviors are due to the wavenumber dispersion, almost absent in [Reference Chiotellis10], but no longer negligible in waveguiding structures such as our periodic LWA and RLSA antennas, as extensively commented in [Reference Fuscaldo7] and [Reference Pavone9]. However, the pulse evolution within the nondiffractive range agrees well with the theoretical 1-D envelopes along the radial and the longitudinal axes, originally obtained in [Reference Fuscaldo7].
Conclusion
In this work, the role of the leakage rate in the generation of limited-diffractive beams (i.e., Bessel beams) and limited-dispersive pulses (i.e., XWs) has been carefully addressed for the first time. A preliminary theoretical analysis is proposed to derive simple criteria for designing an azimuthally-invariant periodic LW radiator, namely a PPW with annular slots. According to these criteria, a simple layout is proposed at 60 GHz and the dispersion analysis of the structure is obtained over a frequency range of 20%. These results are then used for evaluating the performance of the considered device in relation to the generation of Bessel beams and XWs. The effects due to an ideal uniform frequency spectrum and a real Gaussian frequency spectrum have been checked. Numerical results confirm the feasibility of the proposed approach, opening extremely interesting possibilities for the future generation of focusing LWs.
Walter Fuscaldo (S'15) was born in Rome, Italy, in 1987. He received the B.Sc. and M.Sc. (cum laude) degrees in Telecommunications Engineering from “La Sapienza'' University of Rome, Italy, in 2010 and 2013. In 2017, he received the Ph.D. degree (cum laude and with the Doctor Europaeus label) from both the Department of Information Engineering, Electronics and Telecommunications (DIET) and the Institut d'Électronique et de Télécommunications de Rennes (IETR), Université de Rennes 1, Rennes, France, under a cotutelle agreement between the institutions. From September 2014 to December 2014, and from September 2017 to December 2017 he was a Visiting Researcher with the NATO-STO Center for Maritime Research and Experimentation, La Spezia, Italy. From May 2016 to September 2016, he was a Visiting Researcher with the University of Houston, Houston, TX, USA. He is currently working as an Assistant Researcher with the Department of Information Engineering, Electronics and Telecommunications, “La Sapienza”, University of Rome. His current research interests include propagation of leaky waves, surface waves and surface plasmon polaritons, analysis and design of leaky-wave antennas, generation of limited-diffraction limited-dispersion electromagnetic waves, millimeter-wave focusing systems, graphene electromagnetics, metasurfaces, and THz antennas. Dr. Fuscaldo was a recipient of the Yarman-Carlin Student Award at the IEEE 15th Mediterranean Microwave Symposium in 2015, the Young Engineer Prize for the Best Paper presented at the 46th European Microwave Conference in 2016, the IEEE AP-S Student Award, Chapter Center-Southern Italy in 2017, and the Best Paper Award in Electromagnetics and Antenna Theory at the 12th European Conference on Antennas and Propagation in 2018.
Davide Comite (M’ 15) received the M.Sc. (cum laude) in Telecommunications Engineering in 2011 and the Ph.D. degree in Electromagnetics and Mathematical Models for Engineering in 2015, both from “La Sapienza” University of Rome, Italy, where he is currently a Postdoctoral Researcher. He was a visiting PhD student at the Institute of Electronics and Telecommunications of Rennes, University of Rennes 1, France, in 2014 and a Postdoctoral Researcher at the Center of Advanced Communications, Villanova University, PA, USA, in 2015. His scientific interests involve the design of dual-polarized leaky-wave antennas, 2-D periodic leaky-wave antennas and the generation of non-diffracting waves and pulses. He is also interested in the study of the scattering from isotropic and anisotropic natural surfaces as well as the characterization of the GNSS reflectometry over the land. His activity also regards microwave imaging and objects detection performed through GPR, operating both in down-looking as well as forward-looking configurations, and the modelling of the radar signature in forward scatter radar systems. Davide was a recipient of the Marconi Junior Prize, awarded by Fondazione Guglielmo Marconi in 2012 to a young student author of a Master’s degree thesis particularly relevant and important in ICT. He received an honourable mention in the frame of the Minerva Award 2017, awarded by Sapienza University and Fondazione Sapienza to postdoctoral researchers who developed distinguished research activities. He was co-author of the Best Student Paper Award, at SPIE Remote Sensing and Security+Defence International Symposia in 2017, and of the Best Paper Award, Electromagnetics and Antenna Theory section, at the 12th European Conference on Antennas and Propagation in 2018.
Alessandro Boesso was born in Rome, Italy, in 1992. He received the B.Sc. and M.Sc. (cum laude) degrees in Electronic Engineering from “La Sapienza'' University of Rome, Italy, in 2014 and 2017. From October 2017 to May 2018, he worked at Neat s.r.l, Rome, Italy, as a Hardware/Firmware Engineer. He is currently working at Space Engineering s.p.a., Rome, Italy, as a Young Antenna Engineer. His research interests include leaky-wave antennas, millimeter-wave focusing systems, and X-waves.
Paolo Baccarelli received the Laurea degree in Electronic Engineering and the Ph.D. degree in Applied Electromagnetics from “La Sapienza” University of Rome, Italy, in 1996 and 2000, respectively. In 1996, he joined the Department of Electronic Engineering, “La Sapienza” University of Rome, where he was an Assistant Professor from November 2010. From April 1999 to October 1999, he was a Visiting Researcher with the University of Houston, Houston, TX. In 2017, he joined the Department of Engineering, Roma Tre University, Rome, Italy, where he is an Associate Professor. In 2017, he received the National Scientific Qualification for the role of Full Professor of Electromagnetic Fields in Italian Universities. He has co-authored about 230 papers in international journals, conference proceedings, and book chapters. His research interests include analysis and design of planar antennas and arrays, leakage phenomena in uniform and periodic structures, numerical methods for integral equations and periodic structures, propagation and radiation in anisotropic media, metamaterials, graphene, and electromagnetic band-gap structures. Dr. Baccarelli was the recipient of the Giorgio Barzilai Laurea Prize (1994-1995) presented by the former IEEE Central & South Italy Section; he is on the editorial board of international journals and acts as reviewer for more than 20 IEEE, IET, OSA, and AGU journals; he was Secretary of the 2009-European Microwave Week (EuMW 2009) and has been member of the TPCs of several international conferences.
Paolo Burghignoli was born in Rome, Italy, in 1973. He received the Laurea degree (cum laude) in Electronic Engineering and the Ph.D. degree in Applied Electromagnetics from “La Sapienza” University of Rome, Italy, in 1997 and 2001, respectively. In 1997, he joined the Department of Information Engineering, Electronics and Telecommunications, “La Sapienza” University of Rome. In 2004, he was a Visiting Research Assistant Professor with the University of Houston, Houston, TX, USA. From 2010 to 2015, he was an Assistant Professor with “La Sapienza” University of Rome, where he has been an Associate Professor since 2015. In 2017, he received the National Scientific Qualification for the role of Full Professor of Electromagnetic Fields in Italian Universities. He has co-authored “Fast Breaking Papers, October 2007” in electrical engineering and computer science, about metamaterials (paper that had the highest percentage increase in citations in Essential Science Indicators). His current research interests include analysis and design of planar antennas and arrays, leakage phenomena in uniform and periodic structures, numerical methods for integral equations and periodic structures, propagation and radiation in metamaterials, electromagnetic shielding, and graphene electromagnetics. Dr. Burghignoli was a recipient of the Giorgio Barzilai Laurea Prize (1996–1997) presented by the former IEEE Central & South Italy Section, a 2003 IEEE Microwave Theory and Techniques-S Graduate Fellowship, and a 2005 Raj Mittra Travel Grant for Junior Researchers presented at the IEEE AP-S Symposium on Antennas and Propagation, Washington, DC, USA. He is a Senior Member of IEEE and an Associate Editor of IET Electronics Letters and Hindawi International Journal of Antennas and Propagation.
Alessandro Galli received the Laurea degree in Electronic Engineering and the PhD in Applied Electromagnetics, both from “La Sapienza” University of Rome, Italy. Since 1990, he joined the Department of Electronic Engineering (now Department of Information Engineering, Electronics and Telecommunications, DIET) of “La Sapienza” for his research and educational activities. In 2000 he became Assistant Professor and in 2002 Associate Professor at the Faculty of Engineering of the same University. In 2013 he won the National Scientific Qualification as a Full Professor in the sector of Electromagnetics. In his educational activities, he is currently teaching at “La Sapienza” University of Rome a course in Electromagnetic Fields for the Electronics Engineering bachelor degree, and co-teaching courses in Advanced Antenna Engineering, Microwaves, and Engineering Electromagnetics for Electronics Engineering and for Communications Engineering master degrees. Professor Galli is author of about 300 scientific works and of a patent for an invention concerning a novel type of microwave antenna. His scientific interests are focused on topics of theoretical and applied electromagnetics, mainly concerning analysis, design, and test of antennas and of passive components at microwaves, millimeter waves, and terahertz; specific interests are in radiating devices based on leaky waves, dielectric waveguides and resonators, periodic and multilayered printed structures, metamaterials and graphene, with related modeling and numerical aspects. Other research areas of interest involve geoelectromagnetics, microwave plasma heating, and bioelectromagnetics. In 2009 he was the Treasurer of the European Microwave Week (EuMW) and in 2014 he was the General Co-chair of the EuMW. For the 2010-12 and 2013-15 triennium he was elected as the Italian representative of the Board of Directors of the European Microwave Association (EuMA). Since its foundation in 2013, he has been the coordinator of the European Courses on Microwaves (EuCoM), the first European educational institution on microwaves. He is also a member of the European School of Antennas (ESoA). He is Associate Editor of the International Journal of Microwave and Wireless Technologies by Cambridge University Press and of IET Microwaves, Antennas & Propagation by the Institution of Engineering and Technology. Professor Galli won the Barzilai Prize in 1994 for the best scientific work of under-35 researchers at the 10th National Meeting of Electromagnetics. He was the recipient of the Quality Presentation Recognition Award by the Microwave Theory and Techniques (MTT) Society of the Institute of Electrical and Electronics Engineering (IEEE) at the International Microwave Symposium in 1994 and in 1995. Based on a poll among 300 attendants to the ESoA courses, in 2017 he was elected “Best Teacher” out of a competition of more than one hundred international speakers.
