Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-07-07T15:13:22.721Z Has data issue: false hasContentIssue false
  • English
  • Français

Highly miniaturized wideband angular stable linear–circular and linear–cross polarization converter for Ka-band satellite applications

Published online by Cambridge University Press:  03 May 2023

Mohammad Abdul Shukoor Open the ORCID record for Mohammad Abdul Shukoor [Opens in a new window]  and
Sukomal Dey Open the ORCID record for Sukomal Dey [Opens in a new window]
Mohammad Abdul Shukoor
Affiliation:
Department of Electrical Engineering, Indian Institute of Technology Palakkad, Palakkad, Kerala 678557, India
Sukomal Dey*
Affiliation:
Department of Electrical Engineering, Indian Institute of Technology Palakkad, Palakkad, Kerala 678557, India
*
Corresponding author: Sukomal Dey; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work proposes a novel, extremely miniaturized wideband linear–circular and linear–cross metasurface-enabled reflective polarizer. This design comprises a Meander-line structure with horizontal dipoles as the top frequency selective surface, printed on a 1 mm thin-grounded FR-4 substrate. The x/y-polarized incident electromagnetic wave is converted as circularly polarized from 10.60 to 10.92 GHz (LHCP/RHCP), 12.12 to 17.32 GHz (RHCP/LHCP), and 22.72 to 37.76 GHz (LHCP/RHCP) during reflection with 2.97, 35.33, and 49.74% Fractional Bandwidth (FBW). In addition, this design shows linear–cross conversion with a minimum 90% polarization conversion ratio from 11.41 to 12, 19.01 to 22.34, and 40.74 to 46.82 GHz with an FBW of 5.04, 16.11, and 13.89%. The device performance is considerably stable under different oblique incidences, and the polarizer's unitcell is compact with a structural periodicity of 0.089 × 0.064 $\lambda _L^2$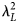, and ultra-thin low-profile substrate thickness of 0.035λL. The proposed prototype is fabricated, and the measured results are in good agreement with the simulated one. This article also mentions how this polarizer could be tuned for dual-band K- and Ka-band satellite applications. The authors believe that the design's novelty lies in the multiband conversion with circular-polarization orthogonality, a highly miniaturized unitcell's volume of 0.199 $\lambda _L^3$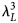/1000, and better angular stability made this design a potential candidate for real-time satellite applications.

Keywords

Angular stablecompactlinear–circularlinear–crossminiaturizedpolarization converterwideband
Type
Metamaterials andPhotonic Bandgap Structures
Information
International Journal of Microwave and Wireless Technologies , Volume 15 , Issue 9 , November 2023 , pp. 1557 - 1569
Check for updates
Copyright
Copyright © Indian Institute of Technology Palakkad, 2023. Published by Cambridge University Press in association with the European Microwave Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Zhao, Y and Alù, A (2011) Manipulating light polarization with ultrathin plasmonic metasurfaces. Physical Review B: Condensed Matter and Materials Physics 84, 205428.CrossRefGoogle Scholar
Li, J, Guo, H, Xu, T, Chen, L, Hang, Z, Zhou, L and Chen, S (2019) Multiple-beam interference-enabled broadband metamaterial wave plates. Physical Review Applied 11, 044042.CrossRefGoogle Scholar
Cheng, H, Tian, J, Li, J, Deng, L, Yu, P and Chen, S (2013) Mid-infrared tunable optical polarization converter composed of asymmetric graphene nanocrosses. Optics Letters 38, 1567–1569.CrossRefGoogle ScholarPubMed
Strikwerda, AC, Fan, K, Tao, H, Pilon, DV, Zhang, X and Averitt, RD (2009) Comparison of birefringent electric split-ring resonator and meanderline structures as quarter-wave plates at terahertz frequencies. Optics Express 17, 136–149.CrossRefGoogle ScholarPubMed
Shukoor, MA and Dey, S (2021) A simple I-shaped wideband linear–linear and linear–circular reflective type polarizer. 2021 IEEE 19th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), pp. 1–2.CrossRefGoogle Scholar
Abdulkarim, Yadgar I, Alkurt, Fatih Özkan, Bakır, Mehmet, Awl, Halgurd N, Muhammadsharif, Fahmi F, Karaaslan, Muharrem, Appasani, Bhargav, Al-Badri, Khalid Saeed Lateef, Zhu, Yuanyuan and Dong, Jian (2022) A polarization-insensitive triple-band perfect metamaterial absorber incorporating ZnSe for terahertz sensing. Journal of Optics 24, 105102.CrossRefGoogle Scholar
Majeed, K, Niazi, SA, Altintas, O, Baqir, MA, Karaslaan, M and Hasar, UC (2022) Multiband polarization-insensitive cartwheel metamaterial absorber. Journal of Materials Science 57, 21392–21401.CrossRefGoogle Scholar
Del Mastro, M, Ettorre, M and Grbic, A (2020) Dual-band, orthogonally-polarized LP-to-CP converter for SatCom applications. IEEE Transactions on Antennas and Propagation 68, 6764–6776.CrossRefGoogle Scholar
Bin Wang, H and Cheng, YJ (2019) Single-layer dual-band linear-to-circular polarization converter with wide axial ratio bandwidth and different polarization modes. IEEE Transactions on Antennas and Propagation 67, 4296–4301.CrossRefGoogle Scholar
Tang, W, Mercader-Pellicer, S, Goussetis, G, Legay, H and Fonseca, NJG (2017) Low-profile compact dual-band unit cell for polarizing surfaces operating in orthogonal polarizations. IEEE Transactions on Antennas and Propagation 65, 1472–1477.CrossRefGoogle Scholar
Shukoor, MA, Dey, S, Koul, SK, Poddar, AK and Rohde, UL (2021) Broadband linear-cross and circular-circular polarizers with minimal bandwidth reduction at higher oblique angles for RCS applications. International Journal of RF and Microwave Computer-Aided Engineering 31, e22693.Google Scholar
Borgese, M, Costa, F, Genovesi, S, Monorchio, A and Manara, G (2018) Optimal design of miniaturized reflecting metasurfaces for ultra-wideband and angularly stable polarization conversion. Scientific Reports 8, 1–11.CrossRefGoogle ScholarPubMed
Zhao, Y, Qi, B, Niu, T, Mei, Z, Qiao, L and Zhao, Y (2019) Ultra-wideband and wide-angle polarization rotator based on double W-shaped metasurface. AIP Advances 9, 085013.CrossRefGoogle Scholar
Huang, X, Yang, H, Zhang, D and Luo, Y (2019) Ultrathin dual-band metasurface polarization converter. IEEE Transactions on Antennas and Propagation 67, 4636–4641.CrossRefGoogle Scholar
Öztürk, Murat, Sevim, Umur Korkut, Altıntaş, Olcay, Ünal, Emin, Akgöl, Oğuzhan, Karaaslan, Muharrem and Sabah, Cumali (2022) Design of a linear to circular polarization converter integrated into a concrete construction for radome applications. International Journal of Microwave and Wireless Technologies 14, 824–831.CrossRefGoogle Scholar
Li, Z, Liu, W, Cheng, H, Chen, S and Tian, J (2015) Realizing broadband and invertible linear-to-circular polarization converter with ultrathin single-layer metasurface. Scientific Reports 5, 1–9.CrossRefGoogle ScholarPubMed
Zeng, Li, Zhang, Hai-Feng, Liu, Guo-Biao and Huang, Tong (2019) Broadband linear-to-circular polarization conversion realized by the solid state plasma metasurface. Plasmonics (Norwell, MA) 14, 1679–1685.CrossRefGoogle Scholar
Arnieri, E, Salucci, M, Greco, F, Boccia, L, Massa, A and Amendola, G (2022) An equivalent circuit/system by design approach to the design of reflection-type dual-band circular polarizers. IEEE Transactions on Antennas and Propagation 70, 2364–2369.CrossRefGoogle Scholar
Lin, B, Lv, L, Guo, J, Liu, Z, Ji, X and Wu, J (2020) An ultra-wideband reflective linear-to-circular polarization converter based on anisotropic metasurface. IEEE Access 8, 82732–82740.CrossRefGoogle Scholar
Zheng, Q, Guo, C and Ding, J (2018) Wideband metasurface-based reflective polarization converter for linear-to-linear and linear-to-circular polarization conversion. IEEE Antennas and Wireless Propagation Letters 17, 1459–1463.CrossRefGoogle Scholar
Wang, Qi, Kong, Xiangkun, Yan, Xiangxi, Xu, Yan, Liu, Shaobin, Mo, Jinjun and Liu, Xiaochun (2019) Flexible broadband polarization converter based on metasurface at microwave band. Chinese Physics B 28, 074205.Google Scholar
Molero Jimenez, C, Menargues, E and Garcia-Vigueras, M (2020) All-metal 3-D frequency-selective surface with versatile dual-band polarization conversion. IEEE Transactions on Antennas and Propagation 68, 5431–5441.CrossRefGoogle Scholar
Doumanis, E, Goussetis, G, Gómez-Tornero, JL, Cahill, R and Fusco, V (2012) Anisotropic impedance surfaces for linear to circular polarization conversion. IEEE Transactions on Antennas and Propagation 60, 212–219.CrossRefGoogle Scholar
Chen, S, Liu, W, Li, Z, Cheng, H and Tian, J (2017) Polarization state manipulation of electromagnetic waves with metamaterials and Its applications in nanophotonics. Metamaterials – Devices and Applications.CrossRefGoogle Scholar
Hebib, S, Aubert, H, Pascal, O, Fonseca, NJG, Ries, L and Lopez, JE (2009) Multiband pyramidal antenna loaded with a cutoff open-ended waveguide. IEEE Transactions on Antennas and Propagation 57, 266–270.CrossRefGoogle Scholar
Naseri, P, Matos, SA, Costa, JR, Fernandes, CA and Fonseca, NJG (2018) Dual-band dual-linear-to-circular polarization converter in transmission mode application to band satellite communications. IEEE Transactions on Antennas and Propagation 66, 7128–7137.CrossRefGoogle Scholar
Shukoor, MA, Dey, S and Koul, SK (2022) Broadband chiral-type linear to linear reflecting polarizer with minimal bandwidth reduction at higher oblique angles for satellite applications. IEEE Transactions on Antennas and Propagation 70, 5614–5622.CrossRefGoogle Scholar
Bin Wang, H, Cheng, YJ and Chen, ZN (2020) Wideband and wide-angle single-layered-substrate linear-to-circular polarization metasurface converter. IEEE Transactions on Antennas and Propagation 68, 1186–1191.CrossRefGoogle Scholar
Luukkonen, Olli, Simovski, Constantin, Granet, Gérard, Goussetis, George, Lioubtchenko, Dmitri, Raisanen, Antti V and Tretyakov, Sergei A (2008) Simple and accurate analytical model of planar grids and high-impedance surfaces comprising metal strips or patches. IEEE Transactions on Antennas and Propagation 56, 1624–1632.CrossRefGoogle Scholar
Li, Fengxia, Chen, Haiyan, Zhang, Linbo, Zhou, Yang, Xie, Jianliang, Deng, Longjiang and Harris, Vincent G (2019) Compact high-efficiency broadband metamaterial polarizing reflector at microwave frequencies. IEEE Transactions on Microwave Theory and Techniques 67, 606–614.CrossRefGoogle Scholar
Khan, MI, Khalid, Z and Tahir, FA (2019) Linear and circular-polarization conversion in X-band using anisotropic metasurface. Scientific Reports 9, 1–11.Google ScholarPubMed
Liu, Xiaobo, Zhang, Jingsi, Li, Wei, Lu, Rui, Li, Lumei, Xu, Zhuo and Zhang, Anxue (2017) Three-band polarization converter based on reflective metasurface. IEEE Antennas and Wireless Propagation Letters 16, 924–927.CrossRefGoogle Scholar
Ibrahim, MS, Mahmoud, A, Awamry, A, Jiang, ZH, Hong, W and Al-Nuaimi, M (2019) Design and fabrication of engineered reflector for wideband linear-to-circular polarization converter. 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, APSURSI 2019 – Proceedings, pp. 1697–1698.CrossRefGoogle Scholar