Introduction
The dielectric property is a crucial physical characteristic of dielectric materials, which describes their electrical behaviors when exposed to external electromagnetic fields [Reference Xiao, Yan, Guo and Chen1]. The permittivity of a material is complex-valued, i.e., 
${\varepsilon _r} = {\varepsilon '_r} - j{\varepsilon ''_r} = {\varepsilon '_r}(1 - j\tan \delta )$, where 
${\varepsilon '_r}$ and 
$\tan \delta $ represent the dielectric constant and loss tangent, respectively. The characterization of material permittivity is important in various fields, including but not limited to the food industry [Reference Athauda, Banerjee and Karmakar2, Reference Zhang, Ruan and Cao3], agriculture [Reference Keshavarz, Lipman, Schreurs and Shariati4], medicine [Reference Kiani, Rezaei and Fakhr5, Reference Kiani and Rezaei6], and polymer materials [Reference Sharma, Gupta and Dankov7]. The planar microwave resonant sensor possesses several advantages, such as high sensitivity, cost-effectiveness, noninvasive, and facile fabrication and integration [Reference Wu and Zhao8, Reference Kiani, Rezaei and Navaei9]. These attributes render it a favorable option to characterize both solid materials and liquid samples. When the material under test (MUT) or liquid under test (LUT) is introduced onto the resonator, the transmission coefficient will be changed. The permittivity of the MUT or LUT can be retrieved by establishing a mathematical relationship between the variations in the transmission coefficient and the permittivity of the material [Reference Wu, Zhao, Wang, Yuan and Wang10].
Recently, various resonance-based planar microwave sensors have been proposed to characterize both solid materials and liquid samples. A dielectric sensor was presented in reference [Reference Albishi, Badawe, Nayyeri and Ramahi11], employing a splitter–combiner microstrip section loaded with multiple coupled complementary split-ring resonators (CSRRs) to enhance sensitivity. In reference [Reference Sun, Gao, Gao, Gao and Gao12], a high-sensitivity sensor was introduced for simultaneous thickness and permittivity measurements of solid dielectric sheets. This sensor comprises a single-microstrip transmission line coupled with a pair of circular complementary spiral resonators. In reference [Reference Liu and Zhang13], permittivity measurements on low dielectric materials were conducted using an improved sensor based on the complementary square spiral resonator. A dual-mode microstrip sensor using a modified magnetic-LC (MLC) resonator was proposed in reference [Reference Wu, Zhao, Wang, Yuan and Wang14] to retrieve the electromagnetic parameters of magnetodielectric materials, and a differential microstrip lines-based microwave sensor loaded with multiple MLC resonators was proposed in reference [Reference Wu, Zhao and Wang15] to enhance common-mode suppression.
In reference [Reference Wu, Zhao, Wang, Yuan and Wang10], an ultrahigh-sensitivity microfluidic sensor was employed, based on modified complementary electric-LC and split-ring resonator structures, to determine the permittivity of the water–ethanol mixture. In reference [Reference Ebrahimi, Scott and Ghorbani16], a microstrip transmission line loaded with a shunt-connected series LC resonator was utilized to create an ultrahigh-sensitivity microfluidic sensor. In reference [Reference Fan, Zhao, Wang, Liu, Chen and Wang17], an ultrahigh sensitivity sensor for microfluidic applications was achieved by adopting a meander slot in the CSRR. In reference [Reference Gan, Zhao, Liu, Wang, Dong, Wang and Yin18], a differential structure based on the microstrip CSRR was presented, demonstrating high sensitivity for liquid characterization while minimizing unwanted environmental influences. For edible oil detection, a multiple CSRRs-based submersible microwave sensor was proposed in reference [Reference Zhang, Ruan, Wang and Cao19] with high sensitivity, and the evaluation of vegetable oils was performed using a complementary mirror-symmetric S resonator (CMSSR) in reference [Reference Armghan20].
The preceding description highlights the intuitive and prevalent approach of enhancing sensor sensitivity by optimizing the resonator structure. In this study, we propose a dual-band planar microwave sensor based on two pairs of triangular-shaped CSRRs to determine the permittivity of liquids. By integrating a meander slot into the CSRRs and incorporating inter-resonator coupling between the CSRRs, the proposed sensor achieves enhanced sensitivity. The effectiveness of the proposed sensor is validated through circuit modeling, full-wave electromagnetic simulation, and experimental verification.
Sensor structure design
Figure 1(a) shows a planar perspective of the proposed dual-band microwave sensor, featuring a splitter–combiner microstrip segment loaded with two pairs of CSRRs etched into the ground plane. The dual split lines are engineered to have a characteristic impedance of 100 Ω, in contrast to the 50 Ω characteristic impedance of the input and output lines. The triangular-shaped CSRRs are designed to facilitate high capacitive coupling with another resonator of a similar configuration [Reference Kazemi and Musilek21]. The sensor employs a substrate of 0.73-mm-thick F4b material, with dimensions of 53 × 26 mm2, a dielectric constant of 2.2, and a loss tangent of 0.001.
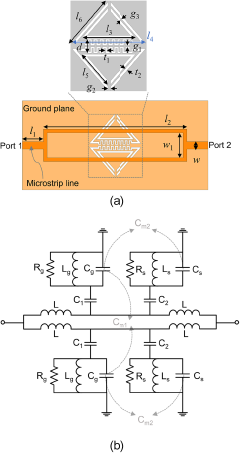
Figure 1. (a) Planar perspective of the proposed microwave dual-band sensor and (b) its equivalent lumped circuit model.
Figure 1(b) shows the associated lumped circuit model. Within this model, C 1 and C 2 are the coupling capacitance between the transmission line and the CSRRs, while L is the inductance of the transmission line. The parameters C g, L g, and R g correspond to the effective capacitance, inductance, and resistance of the modified CSRR combined with a meander slot (M-CSRR). In parallel, C s, L s, and R s are the effective capacitance, inductance, and resistance of the CSRR without a meander slot. C m1 is the mutual capacitance between two M-CSRRs, whereas C m2 is the mutual capacitance modeling the inter-resonator coupling between an CSRR and a M-CSRR. Given the low coupling between the splitter sections, the resonance frequencies of both the M-CSRR and CSRR can be approximated using the subsequent equation [Reference Albishi, Badawe, Nayyeri and Ramahi11]:
\begin{equation}{f_{{\text{M-CSRR}}}} = \frac{1}{{2\pi \sqrt {{L_g}\left( {{C_1} + {C_g} - {C_{m1}} - {C_{m2}}} \right)} }}\end{equation}
\begin{equation}{f_{{\text{CSRR}}}} = \frac{1}{{2\pi \sqrt {{L_s}\left( {{C_2} + {C_s} - {C_{m2}}} \right)} }}\end{equation}The geometrical parameters of the sensor are detailed in Table 1, and its transmission coefficient is obtained using the frequency domain simulator in Computer Simulation Technology (CST)microwave studio. Then, using the optimization toolbox in Keysight Advanced Design System (ADS)’s circuit model simulator, the circuit parameters are extracted, as shown in Table 2. The transmission coefficients obtained by the CST simulation and circuit model shown in Figure 2 demonstrate good agreement. Notably, the sensor exhibits two distinct transmission zeros at 2.8 and 4.85 GHz resonance frequencies, respectively.
Figure 2. Transmission coefficients of the sensor obtained by the CST simulation and circuit model.
Table 1. Geometrical parameters of the sensor (Unit: mm)
Table 2. Extracted circuit parameters
Table 3 presents the simulated transmission curves and normalized electric field magnitude distributions of the different design stages of the proposed sensor. A comparison between the electric field distributions of the CSRRs-based sensor and M-CSRRs-based sensor reveals that incorporating a meander slot into the CSRRs enhances the confinement of the electric field, resulting in heightened sensitivity in the M-CSRRs-based sensor. Furthermore, in accordance with Equation (1), the introduction of inter-resonator coupling capacitance (C m1) between two M-CSRRs renders the resonance frequency of the M-CSRRs-based sensor more sensitive to variations in the relative permittivity of the MUT. By comparing the electric field distributions of the M-CSRRs-based sensor with the proposed sensor (referred to as M-CSRRs & CSRRs-based sensor), it is observed that the addition of another pair of CSRRs in the M-CSRRs & CSRRs-based sensor further enhances the electric field confinement of the two M-CSRRs structure. Similarly, according to Equations (1) and (2), the introduction of inter-resonator coupling capacitances (C m2) between M-CSRRs and CSRRs increases the sensitivity of both the M-CSRRs and CSRRs structures.
Table 3. Design procedure of the proposed sensor
To illustrate the sensitivity of the proposed sensor, a dielectric block with a thickness of 1 mm and varying dielectric constants from 1 to 30 with a step of 3 is modeled and placed on the sensing areas indicated by the white dotted boxes in Table 3. Figure 3 shows the simulated normalized relative frequency shift of the CSRRs-based sensor, M-CSRRs-based sensor, and the proposed sensor. As expected, the M-CSRRs-based sensor exhibits significantly higher sensitivity than the CSRRs-based sensor. In addition, among these, the proposed sensor shows the highest sensitivity to changes in the dielectric constant of the MUT at 2.8 GHz. For instance, for a material with a dielectric constant of 2.5, the proposed sensor provides a 72% improvement in resonance shift compared to the CSRRs-based sensor. Similarly, for a material with a dielectric constant of 22, the proposed sensor offers a 40.4% improvement.
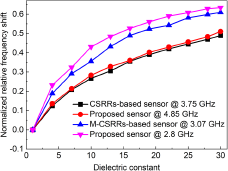
Figure 3. Simulated normalized relative frequency shift versus the dielectric constant varying from 1 to 30 with a step of 3.
The designed sensor can be used in the permittivity sensing of liquid samples. Figure 4 shows a 3-D view of the developed sensor integrated with a polydimethylsiloxane (PDMS) container (
${\varepsilon _r} = 2.8 - j0.0028$) [Reference Sharma, Gupta and Dankov7]. The container has dimensions of 18 mm × 14 mm × 1 mm, while the sensing area’s length, width, and height are 10 mm, 6 mm, and 1 mm, respectively. The simulated transmission responses of the sensor are shown in Figure 5. Compared to the results shown in Figure 2, the two resonant frequencies of the sensor experience a decrease to 2.7 and 4.57 GHz when the PDMS container is loaded. This shift occurs due to the increase in effective capacitance caused by the permittivity of PDMS, consequently leading to a reduction in the resonant frequency.
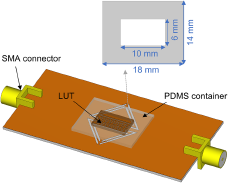
Figure 4. 3-D view of the designed sensor integrated with a PDMS container.
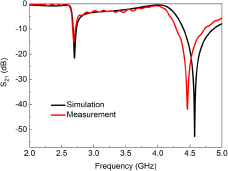
Figure 5. Simulated and measured transmission responses of the proposed sensor.
Experimental validation and discussions
The sensor was fabricated using a standard printed circuit board process. The resulting prototype’s top and bottom views are shown in Figure 6(a), with a PDMS container attached and two 50 Ω SubMiniature version A (SMA)connectors mounted for liquid measurement. The experimental setup is shown in Figure 6(b), and the transmission coefficients are recorded by a Ceyear 3671E vector network analyzer. As shown in Figure 5, the measured resonant frequencies of 2.69 and 4.46 GHz exhibit slight deviations from the simulated values, which can be attributed to factors such as errors in the dielectric constant of the substrate, fabrication, and the testing environment.
Figure 6. (a) Fabricated sensor prototype and (b) experimental setup.
To validate the capability of the proposed sensor in retrieving the permittivity of LUT, an adulteration detection experiment was conducted at room temperature. This involved mixing mineral oil (
${\varepsilon _{r1}} = 2.45 - j0.0387$) into castor oil (
${\varepsilon _{r2}} = 3.37 - j0.3865$) [Reference Galindo-Romera, Javier Herraiz-Martinez, Gil, Martinez-Martinez and Segovia-Vargas22] at different concentration levels. The effective relative permittivity of the adulterated oil is determined using the Maxwell-Garnett mixing rule and summarized in Table 4. The formula is as follows [Reference Barrera and Huff23]:
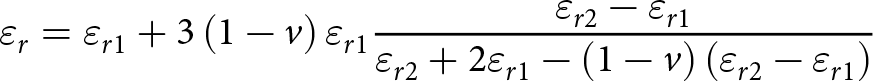\begin{equation}{\varepsilon _r} = {\varepsilon _{r1}} + 3\left( {1 - v} \right){\varepsilon _{r1}}\frac{{{\varepsilon _{r2}} - {\varepsilon _{r1}}}}{{{\varepsilon _{r2}} + 2{\varepsilon _{r1}} - \left( {1 - v} \right)\left( {{\varepsilon _{r2}} - {\varepsilon _{r1}}} \right)}}\end{equation}Table 4. The relative permittivity of the adulterated oil
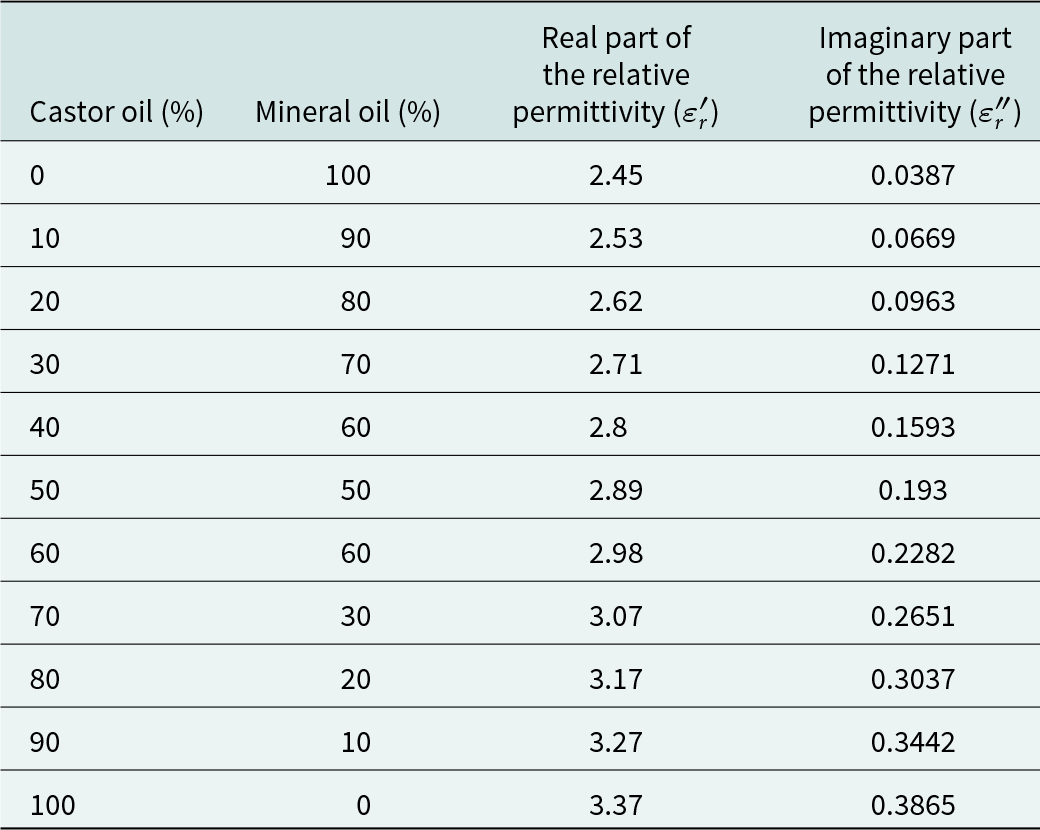
where v represents the volume fraction occupied by mineral oil in the adulterated oil. The oil sample is loaded into the PDMS container using a micropipette, with a consistent volume of 60 μL for each measurement. Following each measurement, the device was cleaned using an alcoholic cotton ball to ensure it returned to its unloaded state and was ready for the next measurement. In the first set of experiments, the volume fraction of castor oil varies from 0% to 100% in increments of 20%. The corresponding transmission responses of the sensor are depicted in Figure 7. As the volume fraction of castor oil increases from 0% to 100%, the first resonant frequency decreases from 2.45 to 2.34 GHz, while the peak attenuation increases from −12.4 to −3.73 dB. Similarly, the second resonant frequency decreases from 4.13 to 3.98 GHz, and the peak attenuation increases from −45.3 to −19.3 dB. To clarify the relationship between the variations in the resonant frequency and peak attenuation in relation to the complex permittivity variations of the test adulterated oils, a nonlinear least square curve fitting method [Reference Ebrahimi, Scott and Ghorbani16] is employed using Matrix Laboratory (MATLAB). The mathematical model is established for the first frequency band, as
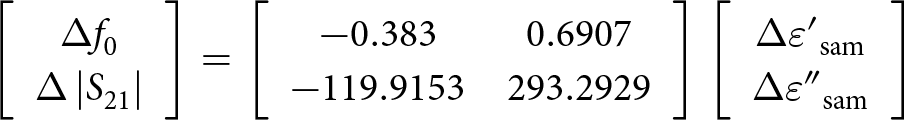\begin{equation}\left[ {\begin{array}{*{20}{c}}
{\Delta {f_0}} \\
{\Delta \left| {{S_{21}}} \right|}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{ - 0.383}&{0.6907} \\
{ - 119.9153}&{293.2929}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{\Delta {{\varepsilon '}_{{\text{sam}}}}} \\
{\Delta {{\varepsilon ''}_{{\text{sam}}}}}
\end{array}} \right]\end{equation}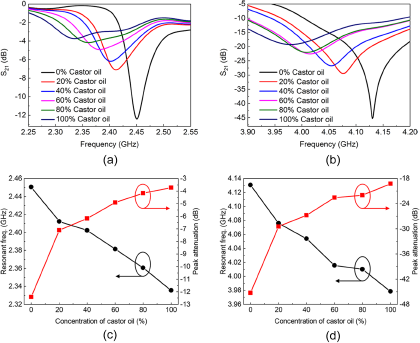
Figure 7. Measured transmission responses for (a) the first and (b) the second frequency band. The resonant frequency and peak attenuation for (c) the first and (d) the second frequency bands. The castor oil volume fraction is increased from 0% to 100% with a step of 20%.
and for the second frequency band, as
\begin{equation}\left[ {\begin{array}{*{20}{c}}
{\Delta {f_0}} \\
{\Delta \left| {{S_{21}}} \right|}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{ - 1.0116}&{2.2535} \\
{ - 353.1321}&{863.7424}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{\Delta {{\varepsilon '}_{{\text{sam}}}}} \\
{\Delta {{\varepsilon ''}_{{\text{sam}}}}}
\end{array}} \right]\end{equation} Where 
$\Delta {\varepsilon '_{{\text{sam}}}} = {\varepsilon '_{{\text{sam}}}} - {\varepsilon '_{{\text{ref}}}}$, 
$\Delta {\varepsilon ''_{{\text{sam}}}} = {\varepsilon ''_{{\text{sam}}}} - {\varepsilon ''_{{\text{ref}}}}$, and 
$\Delta {f_0} = {f_{{\text{sam}}}} - {f_{{\text{ref}}}}$ with the subscript “sam” for oil samples, and “ref” for pure mineral oil. To obtain the permittivity of unknown oil samples, (4) and (5) are inverted as
\begin{equation}\left[ {\begin{array}{*{20}{c}}
{\Delta {{\varepsilon '}_{{\text{sam}}}}} \\
{\Delta {{\varepsilon ''}_{{\text{sam}}}}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{ - 9.946}&{0.0234} \\
{ - 4.0665}&{0.013}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{\Delta {f_0}} \\
{\Delta \left| {{S_{21}}} \right|}
\end{array}} \right]\end{equation}and
\begin{equation}\left[ {\begin{array}{*{20}{c}}
{\Delta {{\varepsilon '}_{{\text{sam}}}}} \\
{\Delta {{\varepsilon ''}_{{\text{sam}}}}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{ - 11.0732}&{0.0289} \\
{ - 4.5272}&{0.013}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{\Delta {f_0}} \\
{\Delta \left| {{S_{21}}} \right|}
\end{array}} \right]\end{equation}To confirm the reliability of the mathematical models above, adulterated oils with increasing fractions of castor oil, ranging from 10% to 90% in increments of 20%, are tested. The measured transmission coefficients, alongside the extracted resonant frequencies and peak attenuations, are displayed in Figure 8. By incorporating the shifts in resonant frequency and variations in peak attenuation into models (6) and (7), we can derive the relative permittivities of these samples. Figure 9 compares the measured permittivities and the benchmark values listed in Table 4. The overall close match between the measured and reference data affirms the accuracy of the developed model in (6) and (7). Within the first frequency band, the largest uncertainty in measuring the permittivity is found at the concentration of castor oil, 10%. Here, the measured real and imaginary permittivity values are 2.63 and 0.0719, respectively, which differ from the actual values of 2.53 and 0.0669. This difference translates to measurement errors of 3.95% for the real part and 7.47% for the imaginary part. Within the second frequency band, the maximum uncertainty for the real permittivity measurement occurs at the concentration of castor oil, 90%, where the measured value is 3.15 compared to the actual value of 3.27, resulting in a measurement error of 3.67%. The maximum uncertainty in measuring the imaginary permittivity also appears at the 10% castor oil concentration, with a measured value of 0.0627 versus the actual value of 0.0669, leading to a measurement error of 6.28%. These errors are attributed to inevitable factors such as manual operation, measurement tool accuracy, and ambient temperature. Moreover, the accuracy of the developed mathematical models can greatly affect the derived permittivity values of the tested oil samples. Thus, measurement errors can be further reduced by establishing high-order mathematical models.
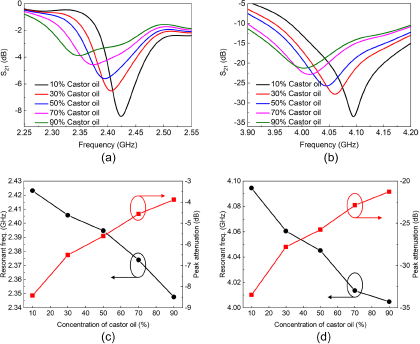
Figure 8. Measured transmission responses for (a) the first and (b) the second frequency band. The resonant frequency and peak attenuation for (c) the first and (d) the second frequency bands. The castor oil volume fraction is increased from 10% to 90% with a step of 20%.
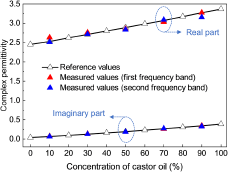
Figure 9. Comparison between the measured and actual values of the permittivity.
Table 5 comprehensively compares the proposed sensor with other relevant literature on oil detection. The comparison includes sensor type, resonant frequency (
${f_0}$), Q-factor, range of dielectric constant (
${\varepsilon '_r}$), frequency detection resolution (FDR), sensitivity (S), liquid sample volume (S.V.), and size. The Q-factor is calculated using formula
\begin{equation}Q = \frac{{{f_0}}}{{\Delta {f_{ + 3dB}}}}\end{equation}Table 5. Comparison between other relevant literature on oil detection with the proposed sensor
where 
${f_0}$ is the central frequency, and 
$\Delta {f_{ + 3dB}}$ is the +3 dB bandwidth. The measured Q-factor values of the sensor are 107 and 510 at frequencies of 2.69 and 4.46 GHz, respectively. The FDR is defined as [Reference Kiani, Rezaei and Fakhr5]
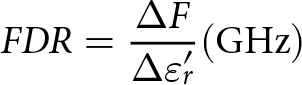\begin{equation}FDR = \frac{{\Delta F}}{{\Delta {{\varepsilon}_r '}}}({\text{GHz}})\end{equation} where 
$\Delta {\varepsilon '_r}$ denotes the dielectric constant variation and 
$\Delta F$ is the relative frequency shift. As mentioned earlier, the dielectric constant of the adulterated oil increases from 2.45 to 3.37, the resonant frequency of the sensor in the first frequency band shifts from 2.45 to 2.34 GHz, and the resonant frequency of the sensor in the second frequency band shifts from 4.13 to 3.98 GHz. Therefore, the measured FDR values for the two frequency bands of the sensor are 0.12 and 0.16 GHz, respectively. The sensitivity of the sensor is defined as [Reference Wu, Zhao, Wang, Yuan and Wang10]
\begin{equation}S = \frac{{\left| {{f_{{{\varepsilon}_r '}}} - {f_0}} \right|}}{{{f_0}}} \cdot \frac{1}{{{{\varepsilon }_r'} - 1}} \cdot 100\% \end{equation} where 
${f_{{{\varepsilon}_r '}}}$ and 
${f_0}$ represent the resonant frequencies of the sensor with and without the liquid sample loaded, respectively. The measured sensitivity values for the two frequency bands of the sensor are 6.34% and 5.7%, respectively. It is worth noting that these sensors operate at different resonant frequencies. To facilitate comparison, the sensor dimensions are given in units of wavelength in free space.
As shown in Table 5, the sensor in reference [Reference Zhang, Ruan, Wang and Cao19] exhibits higher sensitivity than the proposed sensor. However, it should be noted that the device in referene [Reference Zhang, Ruan, Wang and Cao19] requires immersion in the liquid during testing, resulting in the need for larger sample volumes. Regarding the Q-factor, the proposed sensor has lower Q values than the sensors in both references [Reference Zhang, Ruan, Wang and Cao19] and [Reference Grine, Ammari, Benhabiles, Riabi and Djerafi24], yet it is sufficient to distinguish low-loss oil samples. Overall, the proposed sensor provides high sensitivity while maintaining small liquid volume and a compact size. Furthermore, the utilization of two sensing frequency bands enhances its detection capability, making it an excellent candidate for sensing low-loss liquid analytes and solid materials with a broad dielectric range.
Conclusion
This article introduces a dual-band microwave sensor with high sensitivity for liquid characterization. The sensor design incorporates a splitter–combiner microstrip segment loaded with two pairs of triangular-shaped CSRRs. The sensor improves sensitivity by integrating a meander slot into CSRRs and incorporating inter-resonator coupling between CSRRs. The effectiveness of the proposed design is demonstrated through an oil adulteration detection experiment. The variations in resonant frequency and peak attenuation caused by the presence of the liquid sample allow for the retrieval of its permittivity. The measured results highlight the competitive performance of the proposed sensor, including its high sensitivity, utilization of dual frequency bands, compact size, small sample volume, and low cost. These attributes make it a promising option for real-time quality monitoring, binary mixture analysis, and permittivity measurement of liquid analytes and solid materials. Future enhancements will focus on refining the sensor’s design to accommodate high-loss liquids across a broad dielectric range, potentially integrating an intricate microfluidic channel for applications in biochemistry.
Acknowledgements
This work was supported by the National Key Research and Development Program of China under No. 2020YFA0709800 and the Technology Innovation Guidance Program of Shaanxi Province under Grant 2024QCY-KXJ-177.
Competing interests
The authors report no conflict of interest.
Hong Xiao received the Bachelor and Master degrees in Instrument Science and Technology from North University of China, Shanxi, China, in 2016 and 2019, respectively. She is currently pursuing the PhD degree in Electronic Science and Technology from Xi’an Jiaotong University, Xi’an, China. Her current research interests include microwave sensors.
Sen Yan received the Bachelor and Master degrees in Information and Telecommunication engineering from Xi’an Jiaotong University, China, in 2007 and 2010, respectively, and the PhD degree in Electrical Engineering from KU Leuven, Belgium in 2015. After that, he was a postdoctoral research fellow in the same institute. He obtained “Young Talent Support Plan” of Xi’an Jiaotong University, China in 2017, and is currently a full professor there. Prof. Yan’s current research is focused on microwave metamaterials and metasurfaces, wearable devices and textile antennas, antenna diversity and microwave biosensor.
