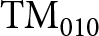Introduction
The mining industry is recognized as one of the most energy-consuming sectors, faces challenges in reducing both energy consumption and operational costs during the rock breakage process, a critical step in mineral extraction. An earlier version of this paper was presented at the SMWD 2023 Conference [Reference Alekajbaf and Dancila1]. Microwave-assisted rock breakage has recently emerged as a promising method to enhance comminution efficiency in mining operations. While microwave technology has been extensively explored for various applications, such as mineral processing, food industry, and healthcare, its potential in rock breakage has remained largely unexplored until recently [Reference Hassani, Nekoovaght and Gharib2]. This innovative approach seeks to break down rocks using high-power microwave sources, generating thermal stress and inducing fractures without the need for traditional mechanical methods. The integration of microwaves into rock breakage processes has the potential to reduce environmental impacts, enhance safety, and increase productivity [Reference Teimoori and Hassani3]. Microwave-assisted rock breakage utilizes high-power microwave sources to induce thermal stress within rocks, leading them to fracture without relying on conventional mechanical techniques. This groundbreaking approach carries the potential to diminish environmental impacts, elevate operational safety, and amplify overall productivity in mining operations [Reference Teimoori and Hassani3]. As the world seeks sustainable alternatives for traditional rock breakage methods, this cutting-edge technology presents a significant opportunity to instigate positive transformation within the industry. The application of microwaves for rock breakage, particularly in deep strata exploration, offers immense potential. Preconditioning rocks with microwave treatment can significantly increase the efficiency of mechanical cutting tools, such as tunnel boring machines. Furthermore, microwave-assisted rock breakage can reduce energy consumption and enhance drilling efficiency. An understanding of the fracture behavior and temperature rise characteristics of rocks in the microwave field is essential for optimizing microwave-assisted rock breakage systems [Reference Gao, Yang, Xie, Ye, Liu, Liu, Tang, Hao, Wang, Wen and Zhou4]. This understanding provides valuable insights into the feasibility and cost-effectiveness of this innovative technology in the mining industry [Reference Teimoori and Hassani3]. As a result, diverse microwave-assisted rock breakage systems are being proposed, utilizing various microwave cavities with differing resonant frequencies and power levels. Various studies have investigated the weakening and fracture characteristics of different rock types, including basalt, gabbro, and granite, in the microwave field. Experiments have been conducted to evaluate the impact of microwave power and irradiation time on the mechanical properties of these hard rocks [Reference Gao, Yang, Xie, Ye, Liu, Liu, Tang, Hao, Wang, Wen and Zhou4]. Pre-conditioning rocks with microwaves prior to mechanical breakage has shown potential for reducing both energy consumption and environmental impacts. Thus, realizing the full potential of microwave-assisted rock breakage requires addressing several challenges, including the efficient application of microwaves, precise modeling, and optimization of the microwave feeder arrangement. Thoroughly understanding and accurately evaluating parameters, such as dielectric properties, thermal and electrical characteristics, and microwave efficiency makes it possible to design and implement economically viable microwave-assisted rock breakage systems [Reference Teimoori and Hassani3]. In this paper, an efficient single-mode 
$\mathrm{TM}_{010}$ cavity is designed as an applicator in a high power microwave-assisted rock comminution system. This work focuses on granite rocks as the target sample. To investigate the electromagnetic behavior of granite rocks, we measure their permittivity using both the reflection method and the developed Kajfez’ algorithm. Therefore, an efficient single-mode 
$\mathrm{TM}_{010}$ cavity which filled by polyether ether ketone (PEEK) to centralize maximum E-field in samples is designed. Also, the simulation and measurement results are reported.
Material characterization
The investigation of permittivity in granite rock is a significant undertaking aimed at characterizing its electromagnetic properties. This measurement plays a pivotal role in understanding the material behavior in the study of rock breaking, contributing to a more comprehensive insight into this field.
Permittivity measurement
Many microwave-based techniques have been developed to measure the exact complex permittivity at specific frequencies for non-destructive testing [Reference Krupka5, Reference Kajfez6]. One of the critical parameters in measuring the permittivity of the complex is the accurate measurement of the quality factor, or Q-factor. The use of the reflection method is one approach that has been introduced for this purpose. In this method, an RF signal is transmitted through a transmission line to the cavity. The impedance mismatch between the transmission line and the cavity results in a reflection of part of the signal. The reflection coefficient is then measured across a frequency range using a vector network analyzer. In this study, the Kajfez’ algorithm is developed in Python to extract the Q-factor of the cavity and calculate the complex permittivity. The experimentally measured S 11 is fitted using the Kajfez’ algorithm to determine the reflection coefficient of the cavity and extract the quality factor [Reference Kajfez6]. In this work, various granite rock samples are measured using a high Q-factor 
$\mathrm{TM}_{010}$ single-mode resonance cavity at 2.45 GHz to investigate their electromagnetic behavior. The permittivity of different granite rock samples are measured employing the reflection method, coupled with a specially developed Kajfez algorithm. The single-mode 
$\mathrm{TM}_{010}$ resonance cavity operating at 2.45 GHz, which is used to accurately measure the complex permittivity of the granite rock is illustrated in Fig. 1. Additionally, an Agilent network analyzer is utilized to measure the s-parameters, and a PC is used to extract the exact values through the developed algorithm.
Figure 1. 
$\mathrm{TM}_{010}$ single mode cavity for granite rock’s complex permittivity measurement.
Resonant cavities are microwave devices that resonate at a desired frequency with a high Q-factor, and they are utilized to measure the exact value of the complex permittivity (
$\varepsilon = \varepsilon{'} - j\varepsilon{''}$) of materials. The single-mode resonance cavity serves this purpose in the dominant resonance mode [Reference Pozar7]. The algorithm developed by Kajfez is designed to estimate the complex permittivity of a sample using a resonance cavity and the reflection coefficient (S 11) measurement method [Reference Kajfez6]. In this approach, the resonance frequency (fl) and Q-factor (Q 0) of the cavity are measured both with and without the sample. The dielectric constant (
$\varepsilon{'}$) and dielectric loss (
$\varepsilon{''}$) are calculated using equations (1) and (2) [Reference McNeal, Jang and Newnham8, Reference Venkatesh9], where Vc and Vs are the volume of the cavity and sample, f 0 and fs are the resonance frequency of the cavity with and without sample, and QLs, and 
$Q_{L0}$ represent the Q-factor of the empty and loaded cavity, calculated using Kajfez’s algorithm. The constant values are determined through the perturbation technique, as detailed in [Reference McNeal, Jang and Newnham8, Reference Venkatesh9]. So, for cylindrical cavities and samples, the volume can be replace with 
$\pi r^2$ [Reference Kanpan, Khansalee, Puangngernmak and Chalermwisutkul10].
\begin{equation}
\varepsilon{'} = 1+0.539\frac{V_{c}\left(f_{0}-f_{s}\right)}{V_{s}f_{0}},
\end{equation}
\begin{equation}
\varepsilon{''} = 0.269\times\frac{V_{c}}{V_{s}}\times\left({\frac{1}{Q_{LS}}-\frac{1}{Q_{L}}}\right).
\end{equation}So,
\begin{equation}
tan\,\delta =\frac{\varepsilon{''}}{\varepsilon{'}}.
\end{equation}Using above literature, to improve accuracy of complex permittivity measurement, the Kajfez’s algorithm developed in Python is used in this work. The developed algorithm could be used for calculating Q-factor using lower points and narrower resonance band [Reference Alekajbaf, Coman, Szaniawski and Dancila12].
Permittivity measurement results
In our designs, an average value for granite permittivity is considered that calculated using measurements from three kinds of available granite rock samples, as shown in Fig. 2. For the initial step of measuring the resonance frequency and Q-factor of the samples, the provided granite samples were placed in the middle of the cavity (as illustrated in Fig. 1). Additionally, Fig. 2 illustrates the measured reflection coefficients (S 11) for both the empty cavity and the cavity loaded with samples. These measurements are conducted using an Agilent network analyzer N5221A.
Figure 2. Granite rock samples with different mixture of minerals and measured S 11 and resonance frequencies for air and granite rock samples.
The fitted graphs by the developed algorithm for the reflection coefficient of empty cavity and loaded by rock samples are shown in Fig. 3. The extracted values of resonance frequency and quality factor for each samples are presented in Table 1. In addition, the complex permittivity permeability are calculated using (1)–(3), these values are given in the table. According to the measured values, an average value can be used to simulate and analyze the electromagnetic behavior of granite rock that is equal to 4−j0.52.
Figure 3. Fitted the reflection coefficient graphs using the developed algorithm for calculating Q-factor of empty and loaded cavity.
Table 1. Extracted and calculated values for Q-factor (
$Q_{\textit{0}}$), resonance frequency (
$f_{\textit{res}}$), and complex permittivity
Applicator design
The applicators play a key role in microwave heating systems. They involve two different types of applicators or cavities: single-mode and multi-mode, each with different heating mechanisms. Single-mode microwave irradiation, known for its ability to effectively focus microwaves and induce rapid heating, is typically employed for localized effects such as heating and cracking on material surfaces. This makes it particularly suitable when coupled with rock cutting tools like drills and boreholes or when rock fragmentations are needed for downstream processes. Multi-mode microwave irradiation is employed for volumetric heating of rocks, serving a more generalized purpose, especially in the mineral processing industry. The distinction between single-mode and multi-mode cavities reflects the varied applications and mechanisms that microwaves offer, from precise localized treatments to more extensive industrial processes [Reference Teimoori and Hassani3, Reference Feng, Gaoming, Li, Zhang, Wan, Tianyang and Yanhua11, Reference Kingman, Jackson, Cumbane, Bradshaw, Rowson and Greenwood13, Reference Kingman, Jackson, Cumbane, Bradshaw, Rowson and Greenwood14]. The single-mode microwave cavity consists of a metallic enclosure and a waveguide as a coupling port. These metallic parts are designed in such a way that the polarization of the electromagnetic field from the microwave signal creates a well-defined standing wave pattern in the cavity space. This specific pattern, characterized by single-mode cavities, allows focusing microwaves in a small volume, and creating a high electric field. Since the electric field and power density are directly proportional, single-mode cavities enable rapid heating, allowing the dielectric material (such as rock) to be placed in positions where maximum heating rates and subsequent maximum mechanical stresses can be achieved [Reference Kingman, Jackson, Cumbane, Bradshaw, Rowson and Greenwood14]. Therefore, designing a single-mode applicator and concentrating the maximum electric field in the center of the granite sample will be the best choice for designing an optimal rock comminution system. In this research, a 
$\mathrm{TM}_{010}$ single mode cavity at 3 GHz is designed as an efficient microwave applicator. The designed applicator is shown in Fig. 4. It can be seen, the designed applicator consists of a 
$\mathrm{TM}_{010}$ cylindrical cavity, a WR340 waveguide coupling port, a granite rock sample, fixing pieces, and a sample holder. Also, the resonance frequency of a 
$TM_{01l}$ single-mode cylindrical cavity are calculated using [Reference Pozar7]:
Figure 4. (a) Designed single-mode 
$\mathrm{TM}_{010}$ cavity at 3 GHz. (b) Cross section of designed cavity.
\begin{equation}
f_{nml} =\frac{c}{2\pi\sqrt{\epsilon{'}\mu{'}}}\sqrt{\left(\frac{P_{nm}}{a}\right)^{2}+\left(\frac{\textit{l}\pi }{d}\right)^{2}},
\end{equation} where a and d are radius and height of cavity which filled by dielectric material with 
$\varepsilon{'}$ and 
$\mu{'}$ characteristics. Also, n, m, and l represent the dominant mode of cavity and Pnm is a constant value which is 2.405 for 
$TM_{01l}$ [Reference Pozar7].
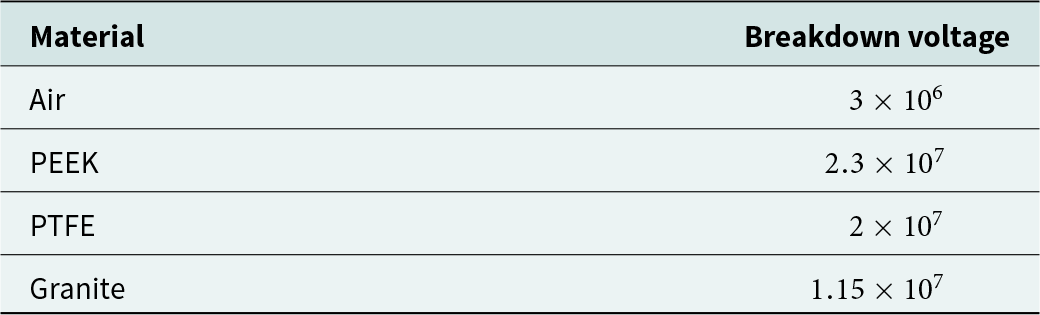
As shown in Fig. 4, the granite rock sample is placed in the middle of the cavity using a dielectric holder. This material is chosen based on the very high electric field density inside the single-mode cavities. To use the cavity for studying rock comminution, paying attention to the breakdown voltage of the material inside the cavity is important for this process. Therefore, PEEK material with higher breakdown voltage than air and rock sample is a good choice to fill the space inside the cavity and keep the rock sample in the center of the cavity. In addition, to compensate the dimensions of the samples and adjust the resonance frequency, small pieces of PTFE have been used inside the sample place. The breakdown voltage of the materials used in the cavity is shown in Table 2.
Table 2. Breakdown voltage of used materials in the designed cavity [Reference Haynes15]
The designed cavity is simulated using HFSS software and its E-field and frequency response (
$S_{11}=-22$ dB) are illustrated in Fig. 5.
Figure 5. Frequency response (S 11) of the designed cavity.
Simulation results
The granite rock sample has been fixed in the center of the designed cavity using the PEEK holder. The distribution of the electric field inside the granite rock sample for different microwave powers radiated at a frequency of 3 GHz is shown in Fig. 6. As can be seen, the maximum of the electric field is concentrated in the center of the granite rock, which will cause it to be crushed if it reaches the breakdown voltage level. The maximum electric field in the center of the granite sample is given in Fig. 6.
Figure 6. E-field distribution inside the granite rock sample for different microwave powers irradiated at 3 GHz.
The maximum electric field in the center of the granite sample, in terms of the amount of radiated power inside the cavity at a frequency of 3 GHz, is shown in Fig. 7. If the breakdown voltage of granite rock considered as the electric field required to crush the rock [Reference Li, Duan, Tan, Chikhotkin and Wang16], it can be seen that by radiating approximately 4.5 mW of microwave power inside the cavity, this level of electric field will be generated within the rock. Before reaching this electric field threshold, the temperature difference created in various compositions of the granite stone will increase the mechanical stress, initiating the crushing process.
Figure 7. Maximum E-field (V/m) inside the granite vs. exposed microwave power inside the 
$\mathrm{TM}_{010}$ cavity.
Experimental results
The fabricated cavity is illustrated in Fig. 8(a), and its frequency response (S 11) is measured using a network analyzer. Considering mechanical fabrication tolerances, an IRIS is employed to optimize the frequency response. The experimental results are presented in Fig. 8(b). The frequency response (S 11) of the optimized fabricated cavity at 3 GHz is approximately −17 dB, as shown in Fig. 8(b).
Figure 8. (a) Fabricated 
$\mathrm{TM}_{010}$ cavity. (b) Measured frequency response (S 11).
Conclusion
The exploration and development of microwave-assisted rock breakage within the mining industry offer a promising avenue for enhancing efficiency and reducing energy consumption. By utilizing a 7.5MW Klystron microwave power source and introducing a 
$\mathrm{TM}_{010}$ single mode cavity at 3 GHz, this study has demonstrated the feasibility of applying microwave technology for rock breakage. The design, simulation, and experimental validation of the microwave cavity have proven effective, with measured frequency responses in line with expectations. This research contributes a significant step toward the practical application of microwave energy in mining processes, opening new possibilities for more sustainable and economically viable methods within the industry.
Acknowledgements
This project has received funding from Vinnova under Project No. 202004462. Also, the authors would like to thank their colleagues in the FREIA Laboratory, Uppsala University, Uppsala, Sweden, for their help and support. Additionally, the authors extend their thanks to Mircea-George Coman for his contributions to Q-factor extraction.
Competing interest
The authors report no conflict of interest.
Yasin Alekajbaf received the B.Sc. degree in Electrical Engineering from Jundi Shapur University of Technology, Dezful, Iran, in 2010, and the M.Sc. degree in Electrical Engineering from Iran University of Science and Technology, Tehran, Iran, in 2013. He completed his Ph.D. degree in Electrical Engineering – Circuit and System at the University of Tehran, Iran, in 2020. He is currently affiliated as a postdoctoral researcher in microwave engineering at Uppsala University, Sweden. His current research interests include RF and microwave circuits, solid-state power amplifiers, microwave cavities, high-power microwave applications, microwave heating, and microwave material processing.
Dragos Dancila completed his Ph.D. in Microwave Engineering at the Université catholique de Louvain in 2011, focusing on research related to RF-MEMS and microfabrication technologies for millimeter-wave components, which was conducted at IMEC in Belgium. Since March 2019, he has held the position of Associate Professor at Uppsala University, where he currently teaches courses in electronics and microwave engineering. His is heading the microwave group and leads research activities within areas such as millimeter-wave antenna arrays and reflectarrays, RF sensors, and high-power highly efficient RF and microwave amplifiers at the FREIA laboratory. In addition to his academic achievements, Dr. Dancila possesses a formal education in Business Management, which he acquired from the Solvay Business School in Brussels. He has also founded the spin-off company Percy Roc AB, with a primary focus on material processing utilizing high-power microwave technology.
Open access
