I. INTRODUCTION
Growing demand for higher data rates along with the global concern on green technologies places challenging requirements on wireless transmitters. To accommodate higher data rates, significant efforts have been made to design multi-band transmitters to support multiple standards in different frequency bands. More specifically, dual-band radiofrequency (RF) power amplifiers (PAs) that can accommodate signals in two different frequency bands have been successfully designed and tested [Reference Cidronali, Giovannelli, Mercanti, Maddio and Manes1–Reference Huynh and Nguyen3].
The non-linear behavior of RF PAs in the transmitter chain causes well-known hardware impairments. The non-linear distortion, which typically is dynamic, contains both in-band distortion and spectral regrowth, i.e. spectral spreading into the adjacent bands, thus interfering with signals in these channels. There are numerous publications on the linearization and efficiency improvement of single-input–single-output (SISO) RF PAs [Reference Anttila, Händel, Mylläri and Valkama4–Reference Guan, Kearney, Yu and Zhu6]. Digital predistortion (DPD) is a well-known technique and is applied to compensate PA non-linear behavior and to improve the overall power efficiency of the RF transmitters. In DPD, an inverse mathematical model of the PA is used and put upstream of the PA to produce a linear output signal. Thus, an accurate mathematical model is required for the linearization of RF PAs.
When dealing with the concurrent dual-band RF PAs, SISO DPD methods cannot be used, since there are two input and two output signals. In multi-band PAs, the non-linear distortions are classified as in-band and cross-band distortions [Reference Bassam, Chen, Helaoui, Ghannouchi and Feng7–Reference Amin, Landin, Händel and Rönnow10]. Both these distortion types should be included in behavioral models and DPD techniques for modeling and linearizing concurrent multi-band PAs.
In recent years, several techniques have been proposed to compensate the non-linear distortions in concurrent dual-band PAs. In [Reference Roblin11], a frequency selective compensation technique is proposed. A large-signal network analyzer was used to characterize the PA's behavior, and to extract DPD coefficients. In [Reference Cidronali, Magrini, Fagotti and Manes12], a dual-band DPD system architecture is proposed. The DPD system architecture used a memory polynomial-based pre-distorter and in the feedback path, a subsampling receiver is used.
One of the most commonly used DPD model structures for concurrent dual-band PA is the two-dimensional (2D)-DPD model proposed in [Reference Bassam, Helaoui and Ghannouchi13] and used in [Reference Liu, Yan and Asbeck9, Reference Chen14–Reference Liu, Chen, Zhou, Zhou and Ghannouchi16]. It is an extension of the SISO parallel Hammerstein (PH) model [Reference Isaksson, Wisell and Ronnow17] to concurrent dual-band PAs. The extension was made by introducing two input signals to the SISO PH model and expanding to the frequency bands of interest. Because of the two signals, the total number of model parameters increases significantly. In [Reference Liu, Chen, Zhou, Zhou and Ghannouchi15] and [Reference Liu, Chen, Zhou, Zhou and Ghannouchi16], the 2D augmented Hammerstein (2D-AH) and 2D modified memory polynomial (2D-MMP) models were proposed. They are simplified variants of the 2D-DPD model and give a comparative performance in terms of normalized mean-square error (NMSE) and adjacent channel power ratio (ACPR) with reduced number of model parameters. However, these models (2D-AH and 2D-MMP) require complex two-step identification processes.
Recently a concurrent dual-band Volterra series was proposed [Reference Qian, Yao, Huang, Yang and Feng18] for modeling and linearization of a concurrent dual-band PAs. However, using the Volterra series for multi-band systems is not feasible due to a high number of model parameters [Reference Zenteno, Amin, Isaksson, Ronnow and Handel19]. In [Reference Eriksson and Fager20], a dual-band generalized memory polynomial (DB-GMP) model was derived by pruning the concurrent dual-band Volterra series. Other 2D memory polynomial models have also been proposed [Reference Zhang, Chen, Ghannouchi and Chen21–Reference Wang, Zhu and Zhu23] to reduce the number of model parameters by applying pruning techniques to the 2D-DPD model. In [Reference Gilabert and Montoro24], a reduced complexity DB-DPD model is proposed for the envelope tracking concurrent dual-band PAs.
In this paper, we derive a novel 2D extended envelope memory polynomial (2D-EEMP) model based on the physical knowledge of a concurrent dual-band RF PA. The derived model is an extension of SISO EEMP model [Reference Landin, Barbé, van Wendy, Isaksson and Händel25]. SISO EEMP model is considered due to a low number of model parameters and its performance [Reference Landin, Barbé, van Wendy, Isaksson and Händel25] compared with SISO PH and GMP models. The derived model includes important cross-modulation terms and to the best of authors knowledge, these terms are not present in any previously published models.
The paper is organized as follows: in Section II, the model derivation is made along with necessary assumptions. Section III describes system identification and performance metrics. The experimental setup is discussed in Section IV. In Section V, the performance of 2D-EEMP behavioral model is evaluated on the commercially available wide-band amplifier. Moreover, the DPD performance of the proposed model is evaluated on two different PAs and the performance comparison against previously published 2D-DPD [Reference Bassam, Helaoui and Ghannouchi13] and DB-GMP [Reference Eriksson and Fager20] models are made. Discussion is made in Section VI and conclusions are drawn in Section VII.
II. THEORY
To derive a mathematical model based on a physical PA model, we consider the block structure in Fig. 1, proposed in [Reference Pedro, Carvalho and Lavrador26]. In Fig. 1, H I (ω) and H O (ω) represent time-invariant filters that describe the input and output matching networks, respectively. The feedback filter F(ω) is a low-pass filter that describes thermal, bias, and trapping effects [Reference Pedro, Carvalho and Lavrador26]. The block K( · ) is the non-linear current source, generating the non-linear distortion [Reference Landin, Barbé, van Wendy, Isaksson and Händel25, Reference Pedro, Carvalho and Lavrador26].

Fig. 1. The model structure proposed in [Reference Pedro, Carvalho and Lavrador26], which represents the bandpass behavior of an RF PA. H I (ω) and H O (ω) are linear filters representing the input and output matching networks, F(ω) is a linear filter for the feedback representing bias modulation and thermal memory effects, and K( · ) is a static non-linearity [Reference Pedro and Maas27]. The x(t) is the input signal, and y(t) is the output signal.
The model shown in Fig. 1 has been used previously to derive PA models for SISO PAs [Reference Landin, Barbé, van Wendy, Isaksson and Händel25, Reference Pedro and Maas27–Reference Wisell and Isaksson29]. We extend the derivation of the SISO EEMP [Reference Landin, Barbé, van Wendy, Isaksson and Händel25] model to concurrent dual-band PAs.
We derive an equivalent low-pass model for input and output signals centered around two different carrier frequencies,
![]() $\omega _{c_1} $
and
$\omega _{c_1} $
and
![]() $\omega _{c_2} $
. Complex equivalent low-pass signals are denoted by, e.g.
$\omega _{c_2} $
. Complex equivalent low-pass signals are denoted by, e.g.
![]() $\tilde u(t)$
; the corresponding RF signal is denote u(t). The relationship between RF signals (or bandpass signals) and the equivalent low-pass signals is [Reference Landin, Barbé, van Wendy, Isaksson and Händel25]
$\tilde u(t)$
; the corresponding RF signal is denote u(t). The relationship between RF signals (or bandpass signals) and the equivalent low-pass signals is [Reference Landin, Barbé, van Wendy, Isaksson and Händel25]
 $$\eqalign{u(t) & = \Re [\tilde u(t)e^{j\omega _c t} ] = \Re [A(t)e^{j(\omega _c t + \phi (t))} ] \cr & = A(t)\cos [\omega _c t + \phi (t)].}$$
$$\eqalign{u(t) & = \Re [\tilde u(t)e^{j\omega _c t} ] = \Re [A(t)e^{j(\omega _c t + \phi (t))} ] \cr & = A(t)\cos [\omega _c t + \phi (t)].}$$
We consider continuous time signals, e.g. u(t) and discrete-time signals, e.g.
![]() $\tilde u(n)$
. Convolution is represented by *, whereas ( · )* denotes the complex conjugate.
$\tilde u(n)$
. Convolution is represented by *, whereas ( · )* denotes the complex conjugate.
We assume that the input signal x(t) in Fig. 1 is composed of two independently modulated signals operating at
![]() $\omega _{c_1} $
and
$\omega _{c_1} $
and
![]() $\omega _{c_2} $$
$\omega _{c_2} $$
 $$\eqalign{x(t) & = x_1(t) + x_2(t) \cr & = A_1(t)\cos [\omega _{c_1}t + \phi _1(t)] + A_2(t)\cos [\omega _{c_2}t \cr & + \phi _2(t)].}$$
$$\eqalign{x(t) & = x_1(t) + x_2(t) \cr & = A_1(t)\cos [\omega _{c_1}t + \phi _1(t)] + A_2(t)\cos [\omega _{c_2}t \cr & + \phi _2(t)].}$$
Here A i (t) and ϕ i (t) are the amplitude and phase modulation of carrier c i , respectively. We assume that the frequency dependance of H I (ω) is negligible [Reference Landin, Barbé, van Wendy, Isaksson and Händel25] and hence,
where h I,1, h I,2 are the filter gain, and τ 1, τ 2 are delays. This assumption is reasonable, as a strong frequency dependence would degrade the EVM (error vector magnitude) of an amplified signal considerably [Reference Landin, Barbé, van Wendy, Isaksson and Händel25].
The block K( · ) in Fig. 1 is assumed to be static [Reference Landin, Barbé, van Wendy, Isaksson and Händel25, Reference Pedro, Carvalho and Lavrador26]. Under this assumption, the output of K( · ) is
 $$\eqalign{v(t) & = K[e(t)] = K[u(t) - f * v(t)] \cr & = \sum\limits_{p = 1}^P a_p [u(t) - f * v(t)]^p,}$$
$$\eqalign{v(t) & = K[e(t)] = K[u(t) - f * v(t)] \cr & = \sum\limits_{p = 1}^P a_p [u(t) - f * v(t)]^p,}$$
where K[ · ] is modeled by a polynomial of order P, and f is the impulse response of the feedback filter F(ω); v(t) is the output and is an infinite sum of loops. The feedback loop is broken after one loop as in [Reference Landin, Barbé, van Wendy, Isaksson and Händel25] and is denoted v 1 (t). This is a well-founded approximation since the loop represents effects that are small relative to the output signals [Reference Pedro, Carvalho and Lavrador26], and it is implicitly assumed in all memory polynomial-type models. By applying the binomial theorem (4) becomes,
 $$v_1 (t) = \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)u^r (t)( - f*v(t))^{p - r}. $$
$$v_1 (t) = \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)u^r (t)( - f*v(t))^{p - r}. $$
Since the feedback loop is broken after one round and no additional filtering is taking place,
![]() $f*v(t)$
can be approximated by [Reference Landin, Barbé, van Wendy, Isaksson and Händel25],
$f*v(t)$
can be approximated by [Reference Landin, Barbé, van Wendy, Isaksson and Händel25],
 $$f*v(t) = f*\sum\limits_{q = 1}^P a_q u^q (t).$$
$$f*v(t) = f*\sum\limits_{q = 1}^P a_q u^q (t).$$
 $$v_1 (t) = \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)u^r (t)\left( { - f*\sum\limits_{q = 1}^P a_q u^q (t)} \right)^{p - r}. $$
$$v_1 (t) = \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)u^r (t)\left( { - f*\sum\limits_{q = 1}^P a_q u^q (t)} \right)^{p - r}. $$
Inserting the dual-band input signal in (3) into (7) and applying the binomial theorem twice results in
 $$\eqalign{v_1 (t) = & \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)(u_1 (t) + u_2 (t))^r \cr&\quad \left( {f*\sum\limits_{q = 1}^P a_q (u_1 (t) + u_2 (t))^q} \right)^{p - r} \cr = & \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)\sum\limits_{k = 0}^r \left( {\matrix{ r \cr {r - k} \cr}} \right)u_1^k (t)u_2^{r - k} (t) \cr&\quad \left( { - f*\sum\limits_{q = 1}^P a_q \sum\limits_{h = 0}^q \left( {\matrix{ q \cr {q - h} \cr}} \right)u_1^h (t)u_2^{q - h} (t)} \right)^{p - r}.} $$
$$\eqalign{v_1 (t) = & \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)(u_1 (t) + u_2 (t))^r \cr&\quad \left( {f*\sum\limits_{q = 1}^P a_q (u_1 (t) + u_2 (t))^q} \right)^{p - r} \cr = & \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)\sum\limits_{k = 0}^r \left( {\matrix{ r \cr {r - k} \cr}} \right)u_1^k (t)u_2^{r - k} (t) \cr&\quad \left( { - f*\sum\limits_{q = 1}^P a_q \sum\limits_{h = 0}^q \left( {\matrix{ q \cr {q - h} \cr}} \right)u_1^h (t)u_2^{q - h} (t)} \right)^{p - r}.} $$
In the present form, (8) result in a large number of terms and in order to simplify, we assume that the dominant terms are those for which p − r = 0 or p − r = 1, i.e. only second-order mixing is allowed as in [Reference Landin, Barbé, van Wendy, Isaksson and Händel25]. Equation (8) can then be further simplified to,
 $$\eqalign{ v_1 (t) &= \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p \sum\limits_{k = 0}^r a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)\left( {\matrix{ r \cr {r - k} \cr}} \right)u_1^k (t)u_2^{r - k} (t)\cr & \quad \left( { - f*\sum\limits_{q = 1}^P \sum\limits_{h = 0}^q a_q \left( {\matrix{ q \cr {q - h} \cr}} \right)u_1^h (t)u_2^{q - h} (t)} \right).} $$
$$\eqalign{ v_1 (t) &= \sum\limits_{p = 1}^P \sum\limits_{r = 0}^p \sum\limits_{k = 0}^r a_p \left( {\matrix{ p \cr {p - r} \cr}} \right)\left( {\matrix{ r \cr {r - k} \cr}} \right)u_1^k (t)u_2^{r - k} (t)\cr & \quad \left( { - f*\sum\limits_{q = 1}^P \sum\limits_{h = 0}^q a_q \left( {\matrix{ q \cr {q - h} \cr}} \right)u_1^h (t)u_2^{q - h} (t)} \right).} $$
The terms in (9) are centered at all possible intermodulation frequencies. However, in the following we have restricted ourself to the terms that are centered around
![]() $\omega _{c_1} $
and
$\omega _{c_1} $
and
![]() $\omega _{c_2} $
, respectively.
$\omega _{c_2} $
, respectively.
For signal components located at
![]() $\omega _{c_1} $
, the exponent of u
1 (t) must be odd and exponent of u
2 (t) must be even and vice versa for
$\omega _{c_1} $
, the exponent of u
1 (t) must be odd and exponent of u
2 (t) must be even and vice versa for
![]() $\omega _{c_2} $
. These requirements are straight forward if the analytical signal of (9) is considered in frequency domain (cf. [Reference Fager, Bland, Hausmair, Chani and Eriksson30] and references therein). To find terms of a certain non-linear order in (9), we use a method similar to that in [Reference Schetzen31]. Table 1 lists all possible third-order non-linear terms located at
$\omega _{c_2} $
. These requirements are straight forward if the analytical signal of (9) is considered in frequency domain (cf. [Reference Fager, Bland, Hausmair, Chani and Eriksson30] and references therein). To find terms of a certain non-linear order in (9), we use a method similar to that in [Reference Schetzen31]. Table 1 lists all possible third-order non-linear terms located at
![]() $\omega _{c_1} $
and the corresponding equivalent low-pass terms.
$\omega _{c_1} $
and the corresponding equivalent low-pass terms.
Table 1. Third-order terms and equivalent low-pass representations at
![]() $\omega _{c_1} $
.
$\omega _{c_1} $
.

The assumption that F(ω) has a low-pass characteristics that does not pass any signal components at
![]() $\omega _{c_1} $
or above, gives that the terms in rows 1, 3a, 3b, 5, 6b, 8, 9a, and 9b, of Table 1 are filtered out. The third-order terms within the bandwidth of interest at
$\omega _{c_1} $
or above, gives that the terms in rows 1, 3a, 3b, 5, 6b, 8, 9a, and 9b, of Table 1 are filtered out. The third-order terms within the bandwidth of interest at
![]() $\omega _{c_1} $
after filtering are those given in Table 2. In Table 2, the term in row 3 is a second-order difference term that down-converts to
$\omega _{c_1} $
after filtering are those given in Table 2. In Table 2, the term in row 3 is a second-order difference term that down-converts to
![]() $\omega _{c_1} - \omega _{c_2} $
, then filtered by F(ω) and finally up-converts back to
$\omega _{c_1} - \omega _{c_2} $
, then filtered by F(ω) and finally up-converts back to
![]() $\omega _{c_1} $
. The inclusion of this term is of importance as the second-order difference term falls on top of the impedance and mixes back as an intermodulation distortion products [Reference Vuolevi and Rahkonen32].
$\omega _{c_1} $
. The inclusion of this term is of importance as the second-order difference term falls on top of the impedance and mixes back as an intermodulation distortion products [Reference Vuolevi and Rahkonen32].
Table 2. Third-order terms and equivalent low-pass representations within the bandwidth of interest at
![]() $\omega _{c_1} $
.
$\omega _{c_1} $
.

The fifth- and seventh-order terms corresponding to the third-order terms in Table 2 are given in Tables 3 and 4, respectively. In Table 3, the terms in rows 11 and 12 are the second-order difference terms that down-converts, then filtered by F(ω) and then up-converts to
![]() $\omega _{c_1} $
. Similarly, in Table 4 the terms in rows 21, 22, and 23 are also second-order difference terms that down-converts and up-converts to
$\omega _{c_1} $
. Similarly, in Table 4 the terms in rows 21, 22, and 23 are also second-order difference terms that down-converts and up-converts to
![]() $\omega _{c_1} $
. Note that these terms to the best of authors knowledge are not included in any of the published models [Reference Bassam, Helaoui and Ghannouchi13, Reference Liu, Chen, Zhou, Zhou and Ghannouchi15, Reference Liu, Chen, Zhou, Zhou and Ghannouchi16, Reference Chen, Zhang, Liu, Ghannouchi, Feng and Liu22], though they are third to seventh-order cross-modulation terms and, hence, might be important for modeling and linearization.
$\omega _{c_1} $
. Note that these terms to the best of authors knowledge are not included in any of the published models [Reference Bassam, Helaoui and Ghannouchi13, Reference Liu, Chen, Zhou, Zhou and Ghannouchi15, Reference Liu, Chen, Zhou, Zhou and Ghannouchi16, Reference Chen, Zhang, Liu, Ghannouchi, Feng and Liu22], though they are third to seventh-order cross-modulation terms and, hence, might be important for modeling and linearization.
Table 3. Fifth-order terms and equivalent low-pass representations within the bandwidth of interest at
![]() $\omega _{c_1} $
.
$\omega _{c_1} $
.

Table 4. Seventh-order terms and equivalent low-pass representations within the bandwidth of interest at
![]() $\omega _{c_1} $
.
$\omega _{c_1} $
.

The terms given in Tables 2–4 are in a form that can be directly translated into a closed form equivalent low-pass representation as
 $$\tilde v_1 (t) = \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^1 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q$$
$$\tilde v_1 (t) = \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^1 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q$$
 $$+ \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^2 \tilde u_1 (t)\left( { - f* \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q} \right)$$
$$+ \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^2 \tilde u_1 (t)\left( { - f* \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q} \right)$$
 $$\eqalign{& + \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 a_{p,q,s}^3 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f* \vert \tilde u_1 (t) \vert ^{2 - s} \vert \tilde u_2 (t) \vert ^s} \right)}$$
$$\eqalign{& + \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 a_{p,q,s}^3 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f* \vert \tilde u_1 (t) \vert ^{2 - s} \vert \tilde u_2 (t) \vert ^s} \right)}$$
 $$\eqalign{& + \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r a_{q,r,s}^4 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{2 - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f* \vert \tilde u_1 (t) \vert ^{r - s} \vert \tilde u_2 (t) \vert ^r} \right)}$$
$$\eqalign{& + \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r a_{q,r,s}^4 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{2 - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f* \vert \tilde u_1 (t) \vert ^{r - s} \vert \tilde u_2 (t) \vert ^r} \right)}$$
 $$+ \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^5 \tilde u_2 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \left( { - f*\tilde u_1 (t)\tilde u_2^ * (t)} \right).$$
$$+ \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^5 \tilde u_2 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \left( { - f*\tilde u_1 (t)\tilde u_2^ * (t)} \right).$$
In order to derive the final 2D-EEMP model, two further assumptions related to the relative power of the linear and non-linear components and to the frequency dependence of H O (ω) and F(ω) are made; without these assumptions, the resulting model will be a 2D-GMP-like model as shown in the appendix.
The assumptions are the same as in [Reference Landin, Barbé, van Wendy, Isaksson and Händel25], i.e. the first assumption is that the power of the linear signal component is significantly larger than the non-linear signal components, which is the common assumption that the PA is weakly non-linear [Reference Wood33]. The second assumption is that the frequency dependence of F(ω) is considerably larger than the frequency dependence of H O (ω), within the excited bandwidths. Frequency dependence here means any deviation from the constant gain and linear phase [Reference Landin, Barbé, van Wendy, Isaksson and Händel25]. As mentioned earlier, the filter H O (ω) in Fig. 1 represents the output matching network, and constant gain and linear phase over a wide bandwidth can be achieved for H O (ω) (cf. [Reference Vuolevi and Rahkonen32] and references therein); however, the same is not true for F(ω) [Reference Vuolevi and Rahkonen32, Reference Vuolevi, Rahkonen and Manninen34].
The model error introduced by these assumptions is negligible compared with the total model error, e.g. the NMSE. For the adjacent channel error power ratio (ACEPR), that focus on the non-linear signal components affected by the filtering, the model error may not be negligible. The above-mentioned assumptions mean that the filtering by H
O
(ω) can be neglected for the non-linear terms but not for the linear ones. Under these assumptions, the output signal
![]() $\tilde y_1 (t)$
at
$\tilde y_1 (t)$
at
![]() $\omega _{c_1} $
can be written as,
$\omega _{c_1} $
can be written as,
 $$+ \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^2 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q$$
$$+ \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^2 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q$$
 $$+ \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^3 \tilde u_1 (t)\left( { - f_{p,q} * \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q} \right)$$
$$+ \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^3 \tilde u_1 (t)\left( { - f_{p,q} * \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q} \right)$$
 $$\eqalign{& + \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 a_{p,q,s}^4 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f_{p,q,s} * \vert \tilde u_1 (t) \vert ^{2 - s} \vert \tilde u_2 (t) \vert ^s} \right)}$$
$$\eqalign{& + \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 a_{p,q,s}^4 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f_{p,q,s} * \vert \tilde u_1 (t) \vert ^{2 - s} \vert \tilde u_2 (t) \vert ^s} \right)}$$
 $$\eqalign{& + \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r a_{q,r,s}^5 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{2 - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f_{q,r,s} * \vert \tilde u_1 (t) \vert ^{r - s} \vert \tilde u_2 (t) \vert ^r} \right)}$$
$$\eqalign{& + \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r a_{q,r,s}^5 \tilde u_1 (t) \vert \tilde u_1 (t) \vert ^{2 - q} \vert \tilde u_2 (t) \vert ^q \cr & \cdot \left( { - f_{q,r,s} * \vert \tilde u_1 (t) \vert ^{r - s} \vert \tilde u_2 (t) \vert ^r} \right)}$$
 $$+ \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^6 \tilde u_2 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \left( { - f_{p,q} *\tilde u_1 (t)\tilde u_2^ * (t)} \right). $$
$$+ \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p a_{p,q}^6 \tilde u_2 (t) \vert \tilde u_1 (t) \vert ^{p - q} \vert \tilde u_2 (t) \vert ^q \left( { - f_{p,q} *\tilde u_1 (t)\tilde u_2^ * (t)} \right). $$
Transforming (11) to discrete-time, sampling, and applying parallelization, i.e. allowing the filters to vary independently between the non-linear orders [Reference Landin, Barbé, van Wendy, Isaksson and Händel25] results in
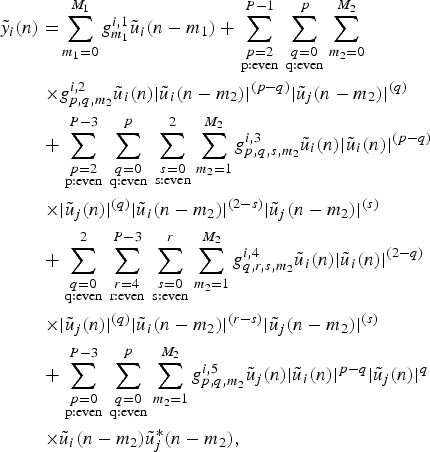 $$\eqalign{\tilde y_i (n) = & \sum\limits_{m_1 = 0}^{M_1} g_{m_1} ^{i,1} \tilde u_i (n - m_1 ) + \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_2 = 0}^{M_2} \cr \times & g_{p,q,m_2} ^{i,2} \tilde u_i (n) \vert \tilde u_i (n - m_2 ) \vert ^{(p - q)} \vert \tilde u_j (n - m_2 ) \vert ^{(q)} \cr + & \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 \sum\limits_{m_2 = 1}^{M_2} g_{p,q,s,m_2} ^{i,3} \tilde u_i (n) \vert \tilde u_i (n) \vert ^{(p - q)} \cr \times & \vert \tilde u_j (n) \vert ^{(q)} \vert \tilde u_i (n - m_2 ) \vert ^{(2 - s)} \vert \tilde u_j (n - m_2 ) \vert ^{(s)} \cr + & \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r \sum\limits_{m_2 = 1}^{M_2} g_{q,r,s,m_2} ^{i,4} \tilde u_i (n) \vert \tilde u_i (n) \vert ^{(2 - q)} \cr \times & \vert \tilde u_j (n) \vert ^{(q)} \vert \tilde u_i (n - m_2 ) \vert ^{(r - s)} \vert \tilde u_j (n - m_2 ) \vert ^{(s)} \cr + & \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_2 = 1}^{M_2} g_{p,q,m_2} ^{i,5} \tilde u_j (n) \vert \tilde u_i (n) \vert ^{p - q} \vert \tilde u_j (n) \vert ^q \cr \times & \tilde u_i (n - m_2 )\tilde u_j^ * (n - m_2 ),} $$
$$\eqalign{\tilde y_i (n) = & \sum\limits_{m_1 = 0}^{M_1} g_{m_1} ^{i,1} \tilde u_i (n - m_1 ) + \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_2 = 0}^{M_2} \cr \times & g_{p,q,m_2} ^{i,2} \tilde u_i (n) \vert \tilde u_i (n - m_2 ) \vert ^{(p - q)} \vert \tilde u_j (n - m_2 ) \vert ^{(q)} \cr + & \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 \sum\limits_{m_2 = 1}^{M_2} g_{p,q,s,m_2} ^{i,3} \tilde u_i (n) \vert \tilde u_i (n) \vert ^{(p - q)} \cr \times & \vert \tilde u_j (n) \vert ^{(q)} \vert \tilde u_i (n - m_2 ) \vert ^{(2 - s)} \vert \tilde u_j (n - m_2 ) \vert ^{(s)} \cr + & \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r \sum\limits_{m_2 = 1}^{M_2} g_{q,r,s,m_2} ^{i,4} \tilde u_i (n) \vert \tilde u_i (n) \vert ^{(2 - q)} \cr \times & \vert \tilde u_j (n) \vert ^{(q)} \vert \tilde u_i (n - m_2 ) \vert ^{(r - s)} \vert \tilde u_j (n - m_2 ) \vert ^{(s)} \cr + & \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_2 = 1}^{M_2} g_{p,q,m_2} ^{i,5} \tilde u_j (n) \vert \tilde u_i (n) \vert ^{p - q} \vert \tilde u_j (n) \vert ^q \cr \times & \tilde u_i (n - m_2 )\tilde u_j^ * (n - m_2 ),} $$
where
![]() $\tilde y_i (n)$
is the output at
$\tilde y_i (n)$
is the output at
![]() $\omega _{c_i} $
, and g
i,1−5 are the model parameters. Equation (12) is the derived 2D-EEMP model.
$\omega _{c_i} $
, and g
i,1−5 are the model parameters. Equation (12) is the derived 2D-EEMP model.
III. SYSTEM IDENTIFICATION
The model in (12) is linear in the parameters and therefore the output signal of a concurrent dual-band PA can be modeled as
where
y
i
is a column vector containing the measured and sampled output signal of the ith output channel,
θ
i
denotes the vector of the model parameters, and
![]() ${\bf \Phi} _i = f(\tilde u_1 (n),\tilde u_2 (n))$
is the regression matrix, whose columns are the basis functions of the derived model. The columns of
${\bf \Phi} _i = f(\tilde u_1 (n),\tilde u_2 (n))$
is the regression matrix, whose columns are the basis functions of the derived model. The columns of
![]() ${\bf \Phi} _i $
are stacked in order of non-linear order and memory depth. An LSE (least-square estimation) technique [Reference Kay35] is used to estimate the model parameters,
${\bf \Phi} _i $
are stacked in order of non-linear order and memory depth. An LSE (least-square estimation) technique [Reference Kay35] is used to estimate the model parameters,
The performance was evaluated in terms of NMSE, ACEPR and ACPR [Reference Landin, Isaksson and Händel36]. The NMSE is defined as
where Φ y (f) is the power spectrum of the measured output signal and Φ e (f) is the power spectrum of the difference between measured and the desired signal; integration is carried out across the available bandwidth. The ACEPR is defined as
 $${\rm ACEPR} = \displaystyle{{\int_{{\rm adj}.\;{\rm ch}.} \Phi _e (f){\kern 1pt} df} \over {\int_{{\rm ch}.} \Phi _y (f){\kern 1pt} df}},$$
$${\rm ACEPR} = \displaystyle{{\int_{{\rm adj}.\;{\rm ch}.} \Phi _e (f){\kern 1pt} df} \over {\int_{{\rm ch}.} \Phi _y (f){\kern 1pt} df}},$$
where the integration in the numerator is performed over the adjacent channel with maximum error power and in the denominator, integration is performed over the input channel. The ACPR is defined as
 $${\rm ACPR} = \displaystyle{{\int_{{\rm adj}.{\rm ch}.} \Phi _y (f){\kern 1pt} df} \over {\int_{{\rm ch}.} \Phi _y (f){\kern 1pt} df}},$$
$${\rm ACPR} = \displaystyle{{\int_{{\rm adj}.{\rm ch}.} \Phi _y (f){\kern 1pt} df} \over {\int_{{\rm ch}.} \Phi _y (f){\kern 1pt} df}},$$
where in the numerator integration is performed over the adjacent channel with the largest amount of power; in the denominator, integration is performed over the input channel band.
To evaluate the complexity of the proposed model and make a fair comparison with the 2D-DPD and DB-GMP models, we measure the complexity in terms of a number of floating point operations (FLOPs). When implementing the DPD on digital platforms, e.g. FPGA (field-programmable gate array), the computational resources are mostly spent on multiplication, addition, and subtraction [Reference Tehrani, Cao, Afsardoost, Eriksson, Isaksson and Fager37]. Therefore, a measure of complexity in FLOPs is relevant. By following the methodology proposed in [Reference Tehrani, Cao, Afsardoost, Eriksson, Isaksson and Fager37], the computational complexity of the behavioral models is evaluated.
IV. EXPERIMENTAL SETUP
The measurement setup used is shown in Fig. 2. The setup consists of two Rohde & Schwartz SMBV100A vector signal generators (VSGs) operating at the carrier frequencies of 2.0 and 2.3 GHz, respectively. The VSGs have baseband and RF coherency. Baseband coherency ensures that the signals from the VSGs are triggered at the same time. The RF coherency [Reference Rönnow, Amin, Alizadeh and Zenteno38] is achieved by feeding the local oscillators of the VSGs with Holzworth HS9003A synthesizer. Note that although it is not required to have RF coherency, however, in [Reference Amin, Landin, Händel and Rönnow10] it was observed that the performance of DPD improved with RF coherency. The output signals of the VSGs are combined using a wide-band power combiner from HP devices (model 87302C). The combined RF signal is fed to the devices under tests (DUTs), and the output of the DUT is down-converted to the IF (intermediate frequency) signal using a wide-band down converter. Digitization of the signal is carried out using an SP Devices ADQ214 analog-to-digital converter (ADC). The ADC has a maximum sampling rate of 400 MHz and a resolution of 14 bits. The sampling frequency and the number of samples are chosen such that an integer number of repeated periods are captured, the process is also known as coherent sampling [39].

Fig. 2. Measurement setup. DUTs were two mini-circuits wide-band amplifier and an Infineon LDMOS high PA. The VSGs used were two R&S SMBV100a.
Three different amplifiers were investigated as the DUTs. The first DUT was a medium high-power wide-band Mini-Circuits ZHL-42W PA and was used for evaluating the behavioral modeling performance of the proposed model. The PA has a small signal gain of 34 dB and output 1 dB compression point of 30 dBm. The Mini-Circuits ZHL-42W PA was excited with two separate WCDMA signals operating at the carrier frequencies of 2.0 and 2.3 GHz. The second DUT was a wide-band Mini-Circuits ZVE-8G+ PA with a small signal gain of 30 dB and an output 1-dB compression point of 30 dBm. The third used DUT was an Infineon high-power RF LDMOS FETs PA (transistor model PTFA210601E) with a gain of 16 dB and an output 1-dB compression point of 48.3 dBm. For DPD of the second and third DUTs, two 5 MHz wide OFDM signals with PAPR (peak-to-average-power-ratio) of more than 10-dB were used, operating at the carrier frequencies of 2.0 and 2.3 GHz. The second and third DUTs were used to evaluate the DPD performance of the proposed model.
V. RESULTS
Fig. 3 shows the measured output spectrum of channel 1/2 when ZHL-42W amplifier was excited with WCDMA signals and Table 5 summarizes the performance of the proposed model when used as a behavioral model. The SISO-EEMP model [Reference Landin, Barbé, van Wendy, Isaksson and Händel25] resulted in the highest model error because the model lacks cross-modulation terms necessary to model concurrent dual-band behavior. The 2D-EEMP resulted in an NMSE of −51.7/−51.6 dB and an ACEPR of −63.1/63.4 dB for channel 1/2. In comparison with the proposed model, the 2D-DPD resulted in largest model error with the NMSE and ACEPR values of −41.3/−40.8 dB and −55.1/−56.7 dB, for channel 1/2. The DB-GMP model resulted in the lowest model error. However, the DB-GMP resulted in 410 complex-valued model parameters per channel, whereas the proposed model resulted in 138 model parameters and the 2D-DPD resulted in 140 model parameters.

Fig. 3. Measured output spectra of the ZHL-42W amplifier along with the error spectrum of the models. The models are described in the legend.
Table 5. Performance evaluation of the given models in terms of NMSE (dB) and ACEPR (dB) for the ZHL-42W amplifier.

Table 6 summarizes the performance in terms of NMSE, ACPR, and FLOPs of the given models used as DPD algorithm for the ZVE8G+ amplifier and Fig. 4 shows the linearized output spectrum. Without DPD, the measured NMSE and ACPR values for channel 1 are −28.4 and −33.4 dB, respectively, and for channel 2, the NMSE and ACPR values are −29.3 and −36.8 dB, respectively. In comparison with the 2D-EEMP model, the 2D-DPD model resulted in the largest NMSE and ACPR values for both channels, whereas, the 2D-EEMP resulted in the lowest NMSE and ACPR values. The DB-GMP model resulted in the NMSE and ACPR values of −45.9 and −53.6 dB, respectively, for channel 1 and are 0.8–2.2 dB higher than those resulted with the 2D-EEMP model. For channel 2, the different in the performance of 2D-EEMP and DB-GMP is more noticeable, where the 2D-EEMP model results in NMSE and ACPR values that are 4–6 dB lower than those resulted with the DB-GMP model. In terms of a total number of model parameters, the 2D-EEMP resulted in 107 model parameters, whereas 2D-DPD and DB-GMP resulted in 112 and 320 model parameters, respectively. In terms of total number of FLOPs, the 2D-EEMP model resulted in 678 FLOPs, whereas the 2D-DPD and DB-GMP require 696 and 1944 FLOPs, respectively.

Fig. 4. Linearized output spectra of the ZVE8G+ amplifier. The DPD models are described in the legend.
Table 6. Performance evaluation of the given models in terms of NMSE (dB) and ACPR (dB) for the ZVE8G+ amplifier.

Table 7 summarizes the performance of the given models when the Infineon LDMOS PA was investigated and Fig. 5 shows the linearized output spectrum for different models. In comparison with the proposed models, the 2D-DPD resulted in the largest NMSE and ACPR values. The DB-GMP resulted in approximately the same NMSE and ACPR values as the 2D-EEMP model for channel 1. However, for channel 2, the DB-GMP resulted in NMSE and ACPR values that are approximately 2–3 dB higher than those resulted with the 2D-EEMP model.

Fig. 5. Linearized output spectra of the Infineon LDMOS high-power RF PA. The DPD models are described in the legend.
Table 7. Performance evaluation of the given models in terms of NMSE (dB) and ACPR (dB) for the Infineon LDMOS PA.

VI. DISCUSSION
Several assumptions are made to derive the proposed model. For the validity of these assumptions, it can be said that the proposed model performance will degrade severely if the concurrent dual-band PAs completely fails one of the required assumptions. Recently in [Reference Alizadeh, Amin and Rönnow40], self- and cross-Volterra kernels of a 3 × 3 non-linear Multiple-input multiple-output system are analyzed along certain paths in a frequency space to determine the block structure of the system. The technique proposed in [Reference Alizadeh, Amin and Rönnow40] can be extended to concurrent dual-band system and used for the validation of some of the assumptions. The authors believe that the proposed approach of utilizing the available knowledge for the concurrent dual-band PAs to develop behavioral models is a useful method and could lead to the further development of concurrent dual-band behavioral models.
Note that the proposed 2D-EEMP model results in a 2D envelope memory polynomial (2D-EMP) model if M 1 = 0. Recently in [Reference Xia, Huang, Chen and Boumaiza41], a 2D-EMP model is proposed by extending the SISO EMP model for concurrent dual-band case. However, the model in [Reference Xia, Huang, Chen and Boumaiza41] lacks the new cross-modulation terms, which are present in the 2D-EEMP model and 2D-EMP model by restricting M 1 = 0 in (12). Therefore, the authors believe that the proposed approach can help in the understanding of non-linear characteristics of concurrent dual-band PAs.
VII. CONCLUSION
Based on the physical knowledge of a concurrent dual-band PA, a 2D-EEMP model is derived. New cross-modulation terms, which are not present in any previously published models are also found. The cross-modulation terms are of importance for both behavioral model and DPD. The model performance is evaluated both as direct and inverse model on three different commercially available amplifies and the results are compared with previously published 2D-DPD and DB-GMP models. The results indicates that 2D-EEMP model shows substantial performance compared with previously published models.
In terms of model complexity, for DPD, the proposed 2D-EEMP model requires smaller number of FLOPs to achieve the same or higher performance as compared with the number of FLOPs required by the 2D-DPD and DB-GMP models.
APPENDIX
By ignoring the assumptions related to the relative power of linear and non-linear signal components and to the frequency dependence of H O (ω) and F(ω), filtering by H O (ω) cannot be neglected for the non-linear terms. Without these assumptions, the resulting model is as follows:
 $$\eqalign{\tilde y_i (n) = & \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 0}^{M_2} g_{p,q,m_1, m_2} ^{i,1} \tilde u_i (n - m_1 ) \cr&\vert \tilde u_i (n - m_1 - m_2 ) \vert ^{(p - q)} \vert \tilde u_j (n - m_1 - m_2 ) \vert ^{(q)} \cr + & \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 1}^{M_2} g_{p,q,s,m_1, m_2} ^{i,2} \tilde u_i (n - m_1 ) \cr& \vert \tilde u_i (n - m_1 ) \vert ^{(p - q)} \vert \tilde u_j (n - m_1 ) \vert ^{(q)} \cr \times & \vert \tilde u_i (n - m_1 - m_2 ) \vert ^{(2 - s)} \vert \tilde u_j (n - m_1 - m_2 ) \vert ^{(s)} \cr+& \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}}^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 1}^{M_2} g_{q,r,s,m_1, m_2} ^{i,3} \cr \times & \tilde u_i (n - m_1 ) \vert \tilde u_i (n - m_1 ) \vert ^{(2 - q)} \vert \tilde u_j (n - m_1 ) \vert ^{(q)} \cr& \vert \tilde u_i (n - m_1 - m_2 ) \vert ^{(r - s)} \vert \tilde u_j (n - m_1 - m_2 ) \vert ^{(s)} \cr +& \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}}^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 1}^{M_2} g_{p,q,m_1, m_2} ^{i,4} \tilde u_j (n\!-\!m_1 ) \vert \tilde u_i (n\!-\!m_1 ) \vert ^{p - q} \cr& \vert \tilde u_j (n - m_1 ) \vert ^q \tilde u_i (n - m_1 - m_2 )\tilde u_j^ * (n - m_1 - m_2 ).} $$
$$\eqalign{\tilde y_i (n) = & \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}} ^{P - 1} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 0}^{M_2} g_{p,q,m_1, m_2} ^{i,1} \tilde u_i (n - m_1 ) \cr&\vert \tilde u_i (n - m_1 - m_2 ) \vert ^{(p - q)} \vert \tilde u_j (n - m_1 - m_2 ) \vert ^{(q)} \cr + & \sum\limits_{{\scriptstyle p = 2 \atop \scriptstyle {\rm p:even}}} ^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^2 \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 1}^{M_2} g_{p,q,s,m_1, m_2} ^{i,2} \tilde u_i (n - m_1 ) \cr& \vert \tilde u_i (n - m_1 ) \vert ^{(p - q)} \vert \tilde u_j (n - m_1 ) \vert ^{(q)} \cr \times & \vert \tilde u_i (n - m_1 - m_2 ) \vert ^{(2 - s)} \vert \tilde u_j (n - m_1 - m_2 ) \vert ^{(s)} \cr+& \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}}^2 \sum\limits_{{\scriptstyle r = 4 \atop \scriptstyle {\rm r:even}}} ^{P - 3} \sum\limits_{{\scriptstyle s = 0 \atop \scriptstyle {\rm s:even}}} ^r \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 1}^{M_2} g_{q,r,s,m_1, m_2} ^{i,3} \cr \times & \tilde u_i (n - m_1 ) \vert \tilde u_i (n - m_1 ) \vert ^{(2 - q)} \vert \tilde u_j (n - m_1 ) \vert ^{(q)} \cr& \vert \tilde u_i (n - m_1 - m_2 ) \vert ^{(r - s)} \vert \tilde u_j (n - m_1 - m_2 ) \vert ^{(s)} \cr +& \sum\limits_{{\scriptstyle p = 0 \atop \scriptstyle {\rm p:even}}}^{P - 3} \sum\limits_{{\scriptstyle q = 0 \atop \scriptstyle {\rm q:even}}} ^p \sum\limits_{m_1 = 0}^{M_1} \sum\limits_{m_2 = 1}^{M_2} g_{p,q,m_1, m_2} ^{i,4} \tilde u_j (n\!-\!m_1 ) \vert \tilde u_i (n\!-\!m_1 ) \vert ^{p - q} \cr& \vert \tilde u_j (n - m_1 ) \vert ^q \tilde u_i (n - m_1 - m_2 )\tilde u_j^ * (n - m_1 - m_2 ).} $$
The above model will have increased complexity both in terms of total number of model parameters and FLOPs as compared with the proposed, 2D-DPD, and DB-GMP models.
 Shoaib Amin received a degree in Avionics Engineering from the National University of Sciences and Technology, Islamabad, Pakistan in 2008 and M.Sc degree in Electronics from the University of Gävle, Sweden in 2012 and Ph.D. degree in Electrical Engineering from KTH Royal Institute of Technology, Stockholm, in 2015. Currently he is pursuing his Ph.D. degree in Electrical Engineering from KTH Royal Institute of Technology, Stockholm, Sweden. His main research interests are characterization and linearization of high-power multi-band and multi-channel RF PAs.
Shoaib Amin received a degree in Avionics Engineering from the National University of Sciences and Technology, Islamabad, Pakistan in 2008 and M.Sc degree in Electronics from the University of Gävle, Sweden in 2012 and Ph.D. degree in Electrical Engineering from KTH Royal Institute of Technology, Stockholm, in 2015. Currently he is pursuing his Ph.D. degree in Electrical Engineering from KTH Royal Institute of Technology, Stockholm, Sweden. His main research interests are characterization and linearization of high-power multi-band and multi-channel RF PAs.
 Per. N Landin received M.Sc. degree in Engineering Physics from Uppsala University, Sweden, in 2007 and the Ph.D. degree in Telecommunication in 2012 jointly from KTH Royal Institute of Technology, Sweden, and Vrije Universiteit Brussel, Belgium. During 2012–2014, he was a post-doc at Chalmers University, Gothenburg, Sweden. From 2014, he is working with Ericsson. His main research interests are in the field of non-linear high-frequency systems and measurement techniques.
Per. N Landin received M.Sc. degree in Engineering Physics from Uppsala University, Sweden, in 2007 and the Ph.D. degree in Telecommunication in 2012 jointly from KTH Royal Institute of Technology, Sweden, and Vrije Universiteit Brussel, Belgium. During 2012–2014, he was a post-doc at Chalmers University, Gothenburg, Sweden. From 2014, he is working with Ericsson. His main research interests are in the field of non-linear high-frequency systems and measurement techniques.
 Peter Händel received the M.Sc. degree in Engineering Physics and Ph.D. degree in Automatic Control from the Department of Information Technology, Uppsala University, Uppsala, Sweden, in 1987 and 1993, respectively. During 1993–1997, he was with the Research and Development Division, Ericsson Radio Systems AB, Kista, Sweden. Since August 1997, he has been in the School of Electrical Engineering, Royal Institute of Technology (KTH), Stockholm, Sweden, where he currently is Professor and Head of the Department of Signal Processing.
Peter Händel received the M.Sc. degree in Engineering Physics and Ph.D. degree in Automatic Control from the Department of Information Technology, Uppsala University, Uppsala, Sweden, in 1987 and 1993, respectively. During 1993–1997, he was with the Research and Development Division, Ericsson Radio Systems AB, Kista, Sweden. Since August 1997, he has been in the School of Electrical Engineering, Royal Institute of Technology (KTH), Stockholm, Sweden, where he currently is Professor and Head of the Department of Signal Processing.
 Daniel Rönnow received the M.Sc. degree in Engineering Physics and Ph.D. degree in Solid-state Physics from Uppsala University, Uppsala, Sweden, in 1991 and 1996, respectively. He was involved with semiconductor physics at Max-Planck-Institut für Festkörperforschung, Stuttgart, Germany, from 1996 to 1998 and with infrared sensors and systems at Acreo AB, Stockholm, Sweden, from 1998 to 2000. From 2000 to 2004, he was a Technical Consultant and Head of Research with Racomna AB, Uppsala, Sweden. From 2004 to 2006 he was a university lecturer at University of Gävle, Sweden. During 2006–2011 he was a senior sensor engineer at Westerngeco, Oslo Norway, where he worked with signal processing and seismic sensors. In 2011, he became a professor in electronics at University of Gävle. He has been an Associate Professor with Uppsala University since 2000. He has authored or coauthored over 45 peer-reviewed papers and holds eight patents. His current research interests are RF measurement techniques, and linearization of non-linear RF circuits and systems.
Daniel Rönnow received the M.Sc. degree in Engineering Physics and Ph.D. degree in Solid-state Physics from Uppsala University, Uppsala, Sweden, in 1991 and 1996, respectively. He was involved with semiconductor physics at Max-Planck-Institut für Festkörperforschung, Stuttgart, Germany, from 1996 to 1998 and with infrared sensors and systems at Acreo AB, Stockholm, Sweden, from 1998 to 2000. From 2000 to 2004, he was a Technical Consultant and Head of Research with Racomna AB, Uppsala, Sweden. From 2004 to 2006 he was a university lecturer at University of Gävle, Sweden. During 2006–2011 he was a senior sensor engineer at Westerngeco, Oslo Norway, where he worked with signal processing and seismic sensors. In 2011, he became a professor in electronics at University of Gävle. He has been an Associate Professor with Uppsala University since 2000. He has authored or coauthored over 45 peer-reviewed papers and holds eight patents. His current research interests are RF measurement techniques, and linearization of non-linear RF circuits and systems.














