Searching for intelligent signals

‘It is just as unscientific to impute to remote intelligences wisdom and serenity as it is to impute to them irrational and murderous impulses. We must be prepared for either possibility and conduct our searches accordingly’ (Dyson, Reference Dyson1964).

In fact, it is extremely hard, if not impossible to make a judgment on what we can expect about the ‘intelligent nature’Footnote ¹ of ETIS. On the other hand, there seem to be determinate conditions for intelligence to emerge. A critical understanding of any (anthropocentric) imputation to the intelligence of extra-terrestrial species should be judged under the light of the available theory. In as much as we would conclude that the wings of an organism have evolved because flying conferred an advantage to the ancestors of a species, so intelligence must be judged accordingly. Although human intelligence is by far the most prominent, several other species have also surprising levels of cognition, mathematical abilities, capacity to solve problems, memory, etc. Why did those traits evolve in different species? Admittedly, in most cases it is not an easy question to answer. But robust theories can explain why. If the causes and conditions for intelligence to evolve were restricted to only a few scenarios, we would in fact be forced to conclude that any ETIS would necessarily share with us, by pure convergence, analogous histories, as well as other analogous traits (Chela-Flores, Reference Chela-Flores2011, Chapters 11 and 12). But at the moments it is too soon to hypothesize on the subject.

This, however, is an adaptationist argument. Whether selection has been the actual drive for the emergence of intelligence in humans, genetic drift has been involved with more strength than selection, or if the pre-adaptations for intelligence were selected as side effects, we do not know. A popular way to understand the advantages of intelligence has been using the comparative method. Primates, cetaceans and other mammals, as well as some bird species, show considerable degrees of intelligence. This has sometimes been credited to convergent evolution. Nevertheless the understanding at the moments is that there are strong constraints in other species, which avoids or delays the increase in the amount of intelligence. This suggests that intelligence as ours is not likely to evolve again on Earth, certainly not soon. However, this principle of convergence has been repeated in astrobiology as if were a natural law; although the principle should not be underestimated (Chela-Flores, 2012, Chapter 12), we must not overestimate it either. Safe directions for speculations must be guided by experimental and empirical observations, which at the moments are not available in the SETI. We simply do not know whether life is to be founded outside Earth, and much less if intelligent life can evolve. Thus at the moment any speculation is, at best, wishful thinking, if not misleading.

If we would establish a METI project the chances of a response are necessarily favoured, opening the door for gathering knowledge about the possible existence, nature and willingness to communicate of ETIS, potentially establishing METI as a methodology to study other forms of evolution.

Simple games under different behavioural scenarios

Having that in mind that in searching for ‘intelligence’ we are actually searching for ETIS prone to be communicative, in proposing and analysing two scenarios, I will ascribe them with some anthropomorphic names. But these are intended only as mnemonic and operational labels, not as literal imputations or anticipation of the behaviours of ETIS.

By assumption the costs and rewards are taken as equivalent between us and the other communicative societies. On the one hand, we are a very young civilization, and is fairly unlikely that other civilizations are as young as ours (Almár, personal communication), which imposes a strong asymmetry not captured by the games considered in this article. On the other hand, the symmetry is justifiable in as long as the costs are proportional to ‘energetic expenditures’, although it might not be true in economical terms. However, regardless of the behavioural nature of the ETIS, this symmetric assumption allows us to measure: the chances that if we broadcast the outcome will be gainful, what is the expected outcome (gain or loss), and also how often we should broadcast.

Communicative societies

This mimics the current situation of the SETI institute that, although committed to its enterprise of finding ETI signals, is constrained by budget, political interests, etc. In this situation, the decision whether to search or search and broadcast (SB) is not strongly driven by any assessment of potential risks and benefits coming from exogenous sources. Thus, we can assign a zero gain to the SETI project, and say a cost −c, to the METI project. A similar situation applies to the ETIS, which for simplicity we assume to incur on equivalent costs. Detection of a signal would produce a gain ρ, which initially we set as unity (see Table 1 for a summary of mathematical symbols). The payoff matrix is resumed in Table 2.

Table 1. Mathematical symbols

Table 2. General payoff matrix for simple 2 player row-games

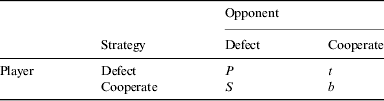
The prisoner's dilemma requires t + b > p > s, and is often parameterized as p = 0, b = 1, t = 2, s = 0. In this article, it is parameterized as p = 0, t = 1 + c, s = −c, b = 1, which does not change the properties of the game, but allows a natural extension to the other kinds of games discussed in the text.

Although detecting a signal will reward us in several ways, sending or not sending a message, makes absolutely no difference, since the gain is the same. However, the costs are higher when we send a message. Thus, even if the reward is higher than the costs the only equilibrium is just to listen (S), because overall, it is cheaper only to search for signals, than to SB a message.

For us, the human species (HS), gaining only depends on whether the ETIS broadcast or not – it is their decision whether to do it. But since our losses are anyway larger if we broadcast, it is better for us to pay less, irrespective if we gain by detecting their signals. As a result, we stay quiet, only listening.

If the situation were equivalent for the ETIS, then they would also decide to be quiet and search, just in case anyone broadcasts. The aftermath is that we end up both searching since it minimizes costs from both sides. This stable situation is known as a (strictly dominant) Nash equilibrium (Nash, Reference Nash1950): both parties are better off only defecting to broadcast, irrespective of the opponent's strategy. An assumption in these kinds of games is that there is no knowledge about the opponent's behaviour or tendency to choose among the strategies.

An extension of this situation arises when the benefits of mutual broadcast (ρ) are much bigger than when receiving a beacon aimed only to get our attention. For example, if we could exchange information with the ETIS, or receive some detailed information about their species or technology, etc. this could be a breakthrough for our society in many aspects. Thus, the reward ρ for actual communication with ETIS is larger than the net detection gain, i.e. ρ >1. In this case there are two pure Nash equilibria: the situation as in the previous scenario of only listening, denoted by the pair (S,S), is still a stable one, as is the communication strategy, where we both parties broadcast and listen (SB,SB). This particular kind of game, termed coordination game, is well known and vastly studied in the literature as a model for the evolution of cooperation (Cooper, Reference Cooper1999; Osborne, Reference Osborne2004 p. 31), and its payoff matrix is depicted in Table 3.

Table 3. Payoff matrix for games between communicative societies

c > 0 ρ > 1.

Belligerent societies

Perhaps the most feared set-up would be a Wellsian, science fiction situation in my opinion, where there is a notable penalty as a consequence of bidirectional broadcasting, for example, because of the possibility of being exploited, attacked, enslaved etc. by the ETIS. This fear seems to be profoundly implanted in us (culturally, historically and otherwise), to the level that the International Academy of Astronautics explicitly advocates peer international consultation before messaging back to any positive SETI signal (Billingham et al. Reference Billingham, Michaud, Tarter, Heidmann and Klein1991).

In this case, we can suppose a game where we pay a huge cost e for being exploited by the ETIS if they detect our signal at the same time that we do not detect theirs. However, if we both broadcast, then for example on the mutual fear of a belligerent move from the other party, only limited information will be shared leading to a basic gain ρ; this is reminiscent of a cold war-like situation. For example, only simple messages revealing our existence but without providing detailed information of our culture, habits, capabilities, technology or about any other resource would be shared. Table 4 resumes the payoff for this game.

Table 4. Payoff matrix for games between belligerent societies

e > > c > 0, c > 0, ρ > 1.

Once more, I assumed a symmetric game, but this need not to be the case. We could introduce an asymmetry in that, for example, we will not be belligerent as a first move. But this does not change the equilibrium. Hence, for simplicity, I will keep the game symmetric. The asymmetry can have an effect if we would consider a repeated game. But for the moments, I am not approaching this problem (although it is certainly interesting and highly relevant).

This last scenario has the same structure as the prisoner's dilemma game. The only Nash equilibrium for a one-shot game (played only once) is again to listen for signals but not to broadcast, (S,S).

The full game with incomplete information

In the analyses of the situations above there was a strong assumption, which is that in each case there was complete information about the reasons why the ETIS could take any strategy. In other words, the payoff matrices were taken as given. In practice, we have no clue which of the situations above (or any other) situations we could face. Thus to make a decision under this uncertainty, it is needed to consider a different structure for the game (Harsanyi, Reference Harsanyi1995). I will keep two artificial assumptions: (1) that we play a single shot game with (2) each of many other civilizations. In our financial analogy, this would be our portfolio. Both possibilities can be relaxed in subsequent works, but the intention of this article is to introduce the methodology by analysing a basic situation.

Before deriving the model in a detailed way, the rationale will be explained. If we knew the behavioural nature of other civilizations (at least qualitatively), there would not be major problem in making a decision whether to broadcast or not, as above. While game theory provides a good framework to model the behaviours, the occurrence of these behaviours is actually unknown. Given this uncertainty, we need to recur to a probabilistic rationalization of the problem. In other words, a frequency of occurrence will be assigned to each type of civilizations. This allows us to compute the average payoff. This average payoff is significant because we are attempting to communicate with (or at least detect) an arbitrary number of civilizations capable of interstellar communication, with varying behaviours (in this case we only consider two). Tentatively, only a proportion of these civilizations are attempting to communicate (i.e. they are broadcasting). These factors are already enough to establish a well-defined game, with which we could in theory, evaluate our strategy. Unfortunately, because to-date there has been no positive beacons we also ignore the distribution of the different types of civilizations, as well as the proportion of them that are broadcasting (if any of them actually occurs). A further way to deal with this uncertainty is to consider that these quantities are a draw from a probability distribution (which for simplicity here is taken as uniform), and compute the expectation of the payoffs. These expected payoffs are still functions of the costs and benefits of the basic games, and although they are independent of the frequencies of the types and the frequency of broadcasting societies, these quantities are not at all disregarded; they are averaged-out. This will convey us with a measure of potential costs and benefits, which allows addressing the question of METI in a quantitative way. In other words, more than a yes/no answer, with this tool a mixed strategy will be calculated, that is, the fraction of times that we should listen, and the fraction of times we should also broadcast.

Mathematical model

To evaluate what our strategy will be, we need to consider the prior probabilities r _i, that the different scenarios (i = communicative, belligerent, etc.) can occur. We can compute the mean payoff of the game as

(1)$$U({\rm \sigma}, {\rm \sigma '}) = \sum\limits_i {r_i V_i ({\rm \sigma}, {\rm \sigma '})}, $$

where V _i(σ, σ′) is the payoff for the strategy (σ, σ′) of the type of ETIS i. Thus, this mean payoff matrix U is averaging over all the types and the entries are the averaged entries. We assume that V(S, S) = 0 and that V(S, SB) = t for all game types (Table 2). In the main example, we will consider only two types, namely communicative (Table 3) and belligerent (Table 4), but different choices are also possible. The mean payoff matrix involving these two types of scenarios is shown in Table 5.

Table 5. Matrix of average payoffs for a compound game

e >> c > 0, c > 0, ρ > 1.

We now assign a probability q for the ETIS playing SB and 1−q for playing S. This gives us our average payoff:

(2)$$U({\rm \sigma,} q) = (1-q)U({\rm \sigma,} S) + q U({\rm \sigma,} SB).$$

In our interest, we want to get the best of any situation, which means to choose which one among the two strategies is the best, given a set of parameters as well as the frequencies r and q. For this, we need to compute the boundary that makes, for example U(SB, q) > U(S, q), which can be computed explicitly by making U(SB, q*) = U(S, q*), which gives the general form:

(3)$$q^* = \displaystyle{{\bar s} \over {t + \bar s + \bar b}}.$$

The last equation would be the mixed Nash equilibrium if the game were being played rationally and with information about the occurrence of the different types. This assumption is waived in this article; instead, q is treated as a random variable, meaning that the frequency of societies that are broadcasting is contingent on unknown factors. Recall that the different entries in U are functions of the frequencies r, therefore q* is a surface parameterized by the variables r, which divides the unit hypercube formed by the variables r into two regions: the one above q*, mathematically written as Ω = {q:U(SB, q*) > U(S, q*)}, and the one below q*, denoted by Ω^c. For instance, in the two-type game there is only one r, and the surface is only a curve given by

(4)$$q^* = \displaystyle{{e(1 - r) + c} \over {e(1 - r) + \rho - 1}}.$$

and is depicted in Fig. 2, where the shading emphasizes the region where U(SB, q) < U(S, q).

Fig. 2. The regions where U(SB, q) < U(S, q) (shaded in grey) are suggestive of adopting the S strategy, because the losses from broadcasting are big compared with the benefits. The white area above suggests adopting the strategy SB, since the gain is greater than when only searching. In this example c = 1, ρ = 200, e = 1000.

The game-theoretical approach commits to the assumption that the ETIS behave rationally, and from that assumption derives the mutually best selfish strategy. The next section introduces a probabilistic approach to deal with the unknown parameters r and q, in order to study how the expected returns of our portfolio behave, and compute our strategy under incomplete information.

Chance of profitable messaging and expected payoffs

At this point I treat q and r as a random variables, by assigning them a probability P(r, q). I define the chance of success Π as the proportion of the space of parameters where broadcasting results gainful. This is given by the proportion of the volume where U(SB, q) > U(S, q), that is the volume Ω above the surface q* (depicted in Fig. 2 for the two-type game). Then, we compute Π as the total volume as:

(5)$$\Pi = \int\limits_{[0,1]^n} {\int\limits_{q \in \Omega} {P(r,q)}} \,{\rm d}q\,{\rm d}.r.$$

and similarly for the chance of a fruitless (or loss-making) effort, Π^c. Here, n + 1 is the number of types (in the two type model, n = 1). Figure 3 shows how the chances where broadcasting is profitable change with some of the parameters. First consider a situation where the costs of the METI project are small, say unity or less, so that the rewards from mutual communication are always larger, i.e. c < ρ. In this situation, the chances of remuneration increase in a monotonous way with ρ, and as also shown in Fig. 2, it is desirable to broadcast in the whole space. The probability is ½ when ρ = 1 + 2e/5 (for large e), which supports the interpretation of Π as the chance of gainful calls: if the rewards are much higher than the costs, the probability increases to one monotonically. If c > ρ, then Π = 0.

Fig. 3. Proportion of the space where it is profitable to broadcast (Π). Π increases with the reward ρ as long as ρ > c, otherwise Π = 0. Solid line c = 0; dashed line c = 100. In both cases e = 1000.

With a similar approach as above, the average payoff on: Ω, U = (σ/Ω), can be defined as

(6)$$\underline U = ({\rm \sigma} |\Omega )\int\limits_{[0,1]^n} {\int\limits_{q \in \Omega} {U({\rm \sigma}, q)P(r,q)}} \,{\rm d}q\,{\rm d}r$$

for any strategy σ. In a similar way, we define U = (σ/Ω^c). These quantities can be calculated in a closed form for the simple games considered here, but the actual expressions of these functions are neither simple nor revealing (see supplementary material (available at http://journals.cambridge.org/IJA) where the derivation is followed step by step, and is also checked with numerical integrations).

As σ takes two strategies and U is defined at the two regions, Ω and Ω^c, it is a matrix. However, it does not represent an average player or anything alike, as the matrix U does; therefore U is not a payoff matrix of a game (in any region Ω either strategy can be played by the ETIS). Instead, U has to be interpreted in a statistical way. However, because it gives our expected payoff as a function of our actions we can employ it to compute the mixed strategy.

Mixed strategy

This section derives and states the central result of this article: the mixed strategy. This quantification follows from weighting the expected payoffs derived above with a frequency F _B that we engage in broadcasting. Every time a star is scanned for SETI signals (under the assumption that it harvests a civilization capable of radio communication) there is a chance Π that it is profitable to broadcast. But we ignore whether that is the case. Our best action is to find F _B such that we are equally well when we broadcast than when we do not. If we always broadcast, we are susceptible to pay a very high cost which overrides the gains. If we never broadcast we entirely rely on their willingness to communicate. There is a middle point set by equating the average payoff in each case, namely:

(7)$$\underline U = (SB|\Omega )F_B + \underline U (S|\Omega )(1 - F_B ) = \underline U (SB|\Omega ^c )F_B + \underline U (S|\Omega ^c )(1 - F_B ).$$

The left side of the equation is the average payoff if we were on the parameter region where we should broadcast; the right side of the equation is the average payoff if we were on the region where we should not broadcast.

Again, the explicit form of F _B is elaborate (see supplementary material), but its form is shown in Fig. 4 for different parameters.

Fig. 4. A mixed strategy (frequency of METI events) exists when the rewards are smaller than a sixth of costs. For small values of reward, the mixed strategy is well approximated by Eq. (8). The mixed strategy decreases hyperbolically to zero, and for rewards that are greater than the costs of exploitation there is a pure strategy of only searching. In this example c = 1, and from top to bottom e = 10³, 10⁶, 10⁹, 10¹². Black lines: exact result; dashed grey lines: approximation.

F _B decreases with ρ, and when ρ∼e/6 it vanishes. In words: as the rewards increase we should decrease the frequency of METI events. Crucially, when the rewards of communication are greater than a sixth of the risks, we should only search. This counter-intuitive outcome means that as the rewards get higher than the costs, our efforts to make profit can be relaxed. This result is also reflected in Fig. 3, which shows that as ρ increases, the probability of being in the gainful region of the games are greater than ½ and monotonically increases to one. Therefore, with less broadcast events, we are more certain of making a profit, and therefore it becomes less urgent to spend resources in broadcasting because we would have a notable income derived from less investment. The extreme limit of this situation would be realized if all civilizations were broadcasting: there would be little need for us to broadcast because only by scanning their messages we would get enough reward, and a few events of METI would constitute the bulk of the gains. An approximation for the mixed strategy is possible, which requires the assumption that ρ < e/6. In this case we find that for the two-type game

(8)$$F_{\rm B} {\rm \approx 2}\displaystyle{{c + 1} \over e}.$$

If ρ > e/6 there is only a pure strategy with F _B = 0, that is, stay silent. This is the central result of this article. It is remarkable on its simplicity: generally speaking, if we consider that the costs of being exploited, e, are very high, then there is still a frequency of METI events that would not compromise us to the degree of such costs. Although F _B might be very low, the large number of stars being surveyed results in a considerable amount of broadcast events (see Discussion section).

Payoff under the mixed strategy

Recall that by the structure of the game we spend c, but we gain the equivalent amount if we detect a signal effortlessly (plus a small reward from detection). Thus, it is important to keep in mind that these are neto gains (or losses), for they already discount the costs. The mixed strategy defines what will be the average payoff when adopting such a strategy, which is shown in Fig. 5(a) as a function of c, the cost of the project. In the limit when ρ < e/6 the expected gain is approximately

(9)$$\underline U (F_B ) = \displaystyle{{(c + 1)({\rm \rho} + 1)} \over {2e}}\left[ {2\,{\rm Log}\left( {1 + \displaystyle{e \over {\rho - 1}}} \right) - 1} \right].$$

Fig. 5. Expected payoff U(F _B) under the mixed strategy. (a) Roughly, U(F _B) increases linearly with the cost of the METI project. Bottom curves and squares: ρ = 10; upper curves and bullets ρ = 500. (b) U(F _B) increases logarithmically with the rewards for communication. Bottom curves and squares: c = 1. Upper curves and bullets: c = 10. Solid grey line: exact result, dashed line: approximation (Eq. 9), symbols: simulations. In all cases e = 10⁴; the simulations results are averages over 10⁶ replicas.

That is, the gain of METI is proportional to the cost of the project (Fig. 5(a)), and it increases slowly with the reward (Fig. 5(b)). Simulations of the games verify the result above; an averaging over 10⁶ replicas was performed for each parameter combination (Fig. 5, see supplementary material for further details).

Concluding remarks

A paradigm change is necessary in SETI, and a systematic active search should be performed. Do the calculations above support this? First of all using the simple prisoner's dilemma game it was shown that if all civilizations choose the safe side and do not broadcast, the great silence would persist. Second, if we actually consider that the costs for being exploited are so high, it implies that it is as non-profitable to broadcast as not to do it, since it generates losses in any case. If that is indeed our assumption, then it entirely justifies shutting down the SETI project, since we do not expect to detect any positive beacon. However, the mixed games go beyond these assumptions and luckily justify both activities. Furthermore, it suggests that a mixed strategy should be performed, and a quantification for such a scenario has been derived.

As it often happens, game-theoretical models give counter-intuitive results and solutions. The mixed strategy derived here indicates that the more the communication would payoff, the less often we should broadcast. Conversely, when the rewards are lower than the cost of being exploited high, it is when it most desirable to broadcast. The paradox then is that if it is true that it is risky to message, as several SETI scientists hold, these fearing reasons are the ones that justify the METI project. However, it is true that it should not be an undisclosed broadcast.

The importance of framing the problem of METI as an economic one is twofold. On the one hand it is a justification for a continued funding of the SETI program. There are only a few research groups dedicated to this activity, and funding cuts to its central nodes is critical. This is unlike any other research field, where cutting the funding to some groups do not mean the death of the field. Moreover, I expect that, given that other civilizations exist, the program will eventually pay back. The second reason is to have a quantitative framework (which might be refined) in order to assess our potential role in an active communication at a larger scale. Notice that the payoffs are not necessarily in economical terms (although they may have an economic measure, as it was done in this article), thus the gains might be technological or intellectual, etc. Altogether this addresses the question of our relationship towards any possibly existing intelligent civilization, which may become a quantitative question upon detection. This includes an attractive possibility and the establishment of an unprecedented paradigm: it might be us who trigger an active communication among civilizations, and who define the nature of the game.