Published online by Cambridge University Press: 15 July 2022
The Fermi paradox has given rise to various attempts to explain why no evidence of extraterrestrial civilizations was found so far on Earth and in our Solar System. Here, we present a dynamical model for the development of such civilizations, which accounts for self-destruction, colonization and astrophysical destruction mechanisms of civilizations including gamma-ray bursts, type Ia and type II supernovae as well as radiation from the supermassive black hole. We adopt conservative estimates regarding the efficiency of such processes and find that astrophysical effects can influence the development of intelligent civilizations and change the number of systems with such civilizations by roughly a factor of $2$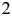 ; potentially more if the feedback is enhanced. Our results show that non-equilibrium evolution allows for solutions in-between extreme cases such as ‘rare Earth’ or extreme colonization, including scenarios with civilization fractions between $10^{-2}$
; potentially more if the feedback is enhanced. Our results show that non-equilibrium evolution allows for solutions in-between extreme cases such as ‘rare Earth’ or extreme colonization, including scenarios with civilization fractions between $10^{-2}$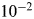 and $10^{-7}$
and $10^{-7}$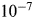 . These would imply still potentially large distances to the next such civilizations, particularly when persistence phenomena are being considered. As previous studies, we confirm that the main uncertainties are due to the lifetime of civilizations as well as the assumed rate of colonization. For SETI-like studies, we believe that unbiased searches are needed considering both the possibilities that the next civilizations are nearby or potentially very far away.
. These would imply still potentially large distances to the next such civilizations, particularly when persistence phenomena are being considered. As previous studies, we confirm that the main uncertainties are due to the lifetime of civilizations as well as the assumed rate of colonization. For SETI-like studies, we believe that unbiased searches are needed considering both the possibilities that the next civilizations are nearby or potentially very far away.