Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T15:25:39.067Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-Dimensional Helioseismic Inversions

Published online by Cambridge University Press:  12 April 2016

J. Schou ,
J. Christensen-Dalsgaard  and
M.J. Thompson
J. Schou
Affiliation:
Institut for Fysik og Astronomi, Aarhus Universitet, Denmarkand High Altitude Observatory, NCAR*, Boulder, Colorado, USA
J. Christensen-Dalsgaard
Affiliation:
Institut for Fysik og Astronomi, Aarhus Universitet, Denmark
M.J. Thompson
Affiliation:
Astronomy Unit, Queen Mary and Westfield College, London, England

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present results of investigations of different inversion methods for inferring from helioseismic observations the rotation rate in the solar interior as a function of radius and latitude, using a mode set similar to that which is expected from the GONG network.

The rotation of a star perturbs the frequency wnlm of a normal mode by

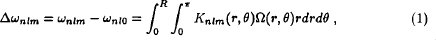
where n, l and m are the mode ‘quantum’ numbers, θ the colatitude, Ω the rotation rate and Knlm a known function. Until now the observations have not been in terms of individual Δwnlm ’s; rather, coefficients ai(n,l) of a parametrization of the m-dependence of Δwnlm have been given. By representing the latitudinal dependence of the rotation rate in terms of an expansion in cos θ, an inversion of the ai, can be carried out as a series of 1-dimensional inversions. Such inversions have been dubbed “1.5-dimensional”. Our present implementation of a 1.5D procedure follows Schou et al. (1992), and uses a1, a3 and a5.

Type
I. Setting the stage: Sun, Stars Galaxies and the Universe
Information
International Astronomical Union Colloquium , Volume 137: Inside the Stars , 1993 , pp. 72 - 74
Copyright
Copyright © Astronomical Society of the Pacific 1993

References

Schou, J., 1991, In Lecture Notes in Physics vol. 388, 93 – 96, eds Gough, D.O. & Toomre, J., Springer, Berlin.Google Scholar
Schou, J., Christensen-Dalsgaard, J., & Thompson, M.J., 1992, Ap. J., 385, L59 – L62.Google Scholar
Sekii, T., 1990. In Lecture Notes in Physics, vol. 367, 337 – 340, eds Osaki, Y. & Shibahashi, H., Springer, Berlin.Google Scholar
Sekii, T., 1991. Publ. Astron. Soc. Japan, 43, 381 – 411.Google Scholar