No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
Efficient tools of investigation of stellar pulsation are the integral relations which link oscillation frequencies to the static structure of stellar models, as provided by the linear theory of pulsation (for a review, see Saio, this conference).
Similarly, oscillation amplitudes and phases, which arise from nonlinear processes, can be related to the stellar structure by means of amplitude equation formalisms (for a review, see Buchler, this conference).
For the simple case of a monoperiodic oscillation, involving only one unstable marginal mode, such a formalism shows that the (limit cycle) radius variations, at time t and mass level m, can be approximated, up to second order of approximation, (Buchler and Goupil, 1984; Buchler and Kovàca, 1986) by:
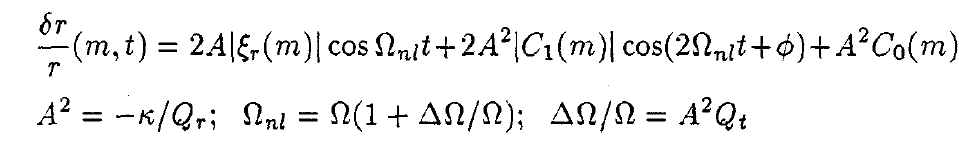
where A, R, Ω, ĸ, £r(m) respectively are the amplitude, stellar radius, linear nonadiabatic frequency, growth rate, radius eigenfunction. Second order nonlinearities generated first harmonic oscillations and change in equilibrium radius about which the star oscillates, as represented by the last two terms in (la) respectively. Analogous expressions are obtained for velocity and light variations, that can be compared with observations.