No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
The inertial range of incompressible MHD turbulence is most conveniently described in terms of counter propagating waves. Shear Alfvén waves control the cascade dynamics. Slow waves play a passive role and adopt the spectrum set by the shear Alfvén waves. Cascades composed entirely of shear Alfvén waves do not generate a significant measure of slow waves. MHD turbulence is anisotropic with energy cascading more rapidly along k⊥ than along k‖. Anisotropy increases with k⊥ such that the excited modes are confined inside a cone bounded by 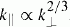 . The opening angle of the cone,
. The opening angle of the cone, 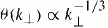 , defines the scale dependent anisotropy. MHD turbulence is generically strong in the sense that the waves which comprise it are critically damped. Nevertheless, deep inside the inertial range, turbulent fluctuations are small. Their energy density is less than that of the background field by a factor θ2(k⊥) « 1. MHD cascades are best understood geometrically. Wave packets suffer distortions as they move along magnetic field lines perturbed by counter propagating wave packets. Field lines perturbed by unidirectional waves map planes perpendicular to the local field into each other. Shear Alfvén waves are responsible for the mapping’s shear and slow waves for its dilatation. The former exceeds the latter by θ−1 (k⊥) » 1 which accounts for dominance of the shear Alfvén waves in controlling the cascade dynamics.
, defines the scale dependent anisotropy. MHD turbulence is generically strong in the sense that the waves which comprise it are critically damped. Nevertheless, deep inside the inertial range, turbulent fluctuations are small. Their energy density is less than that of the background field by a factor θ2(k⊥) « 1. MHD cascades are best understood geometrically. Wave packets suffer distortions as they move along magnetic field lines perturbed by counter propagating wave packets. Field lines perturbed by unidirectional waves map planes perpendicular to the local field into each other. Shear Alfvén waves are responsible for the mapping’s shear and slow waves for its dilatation. The former exceeds the latter by θ−1 (k⊥) » 1 which accounts for dominance of the shear Alfvén waves in controlling the cascade dynamics.