No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
In this paper the method of determination of the planetary perturbations is proposed which is a modification of Dziobek-Brouwer’s method [1,2]. For the simplicity the case of two mutually disturbing planets is considered. In the original version of the method the perturbations of rectangular planetary coordinates are presented by means of the formal integrals
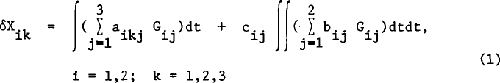
where index i corresponds to the number of the planet; δXik are perbations of Xik coordinates; Gik – components of the perturbating accelerations. The coefficients of aik, cik bij are the well-known functions of the coordinates of the elliptic motion which can be developed as double Fourier series in mean longitudes. The denominators in Davis’ formulas [3] for these coefficients contain the eccentricities. For this reason Musen [4] expressed an opinion that Brouwer’s method would lose its effectiveness when small eccentricities are involved. These fictitious peculiarities are eliminated in the present paper by means of trivial transformations and the expressions for the coefficients are given in a simple symmetric form.