No CrossRef data available.
Article contents
Charge Densities above Pulsar Polar Caps
Published online by Cambridge University Press: 12 April 2016
Extract
A simplified model provided the framework for our investigation into the distribution of energy and charge densities above the polar caps of a rotating neutron star. We assumed a neutron star with m = 1.4M⊙, r = 10km, dipolar field |B0| = 1012G, B||Ω and Ω = 2Π · (0.5s)−1. The effects of general relativity were disregarded. The induced accelerating electric field E|| reaches E0 = 2.5 · 1013 V m−1 at the surface near the magnetic poles. The current density along the field lines has an upper limit nGJ, when the electric field of the charged particle flow cancels the induced electric field: At the poles nGJ(r = rns, θ = 0) = 1.4 · 1017m−3. The work function (surface potential barrier) EW is approximated by the Fermi energy EF of magnetised matter. Following Abrahams and Shapiro (1992) one needs to revise the surface density from the canonical 1.4 · 108kg m−3 down to ρFe = 2.9 · 107kg m−3. With 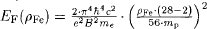 we obtain a value of EF = Ew = 417eV. There are two relevant particle emission processes: Field (cold cathode) emission by quantum-mechanical tunneling of charges through the surface potential
we obtain a value of EF = Ew = 417eV. There are two relevant particle emission processes: Field (cold cathode) emission by quantum-mechanical tunneling of charges through the surface potential 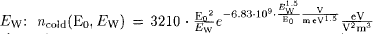 and thermal emission which is a purely classical process. In strong electric fields it is enhanced by the lowering of the potential barrier due to the Schottky effect. The combined Dushman-Schottky equation
and thermal emission which is a purely classical process. In strong electric fields it is enhanced by the lowering of the potential barrier due to the Schottky effect. The combined Dushman-Schottky equation 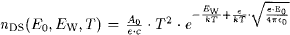 with
with 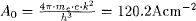 tells us, that at temperatures > 2 · 105K the the Goldreich-Julian current can be supplied thermal emission alone. The surface temperature however has a lower limit in the order of 105 K due to the rotational braking. Therefore, in most cases a sufficient supply of charges for the Goldreich-Julian current is available and the electrical field accelerating the particles will be quenched as a result of their abundance. Otherwise a residual equilibrium electric field Eeq remains with:
tells us, that at temperatures > 2 · 105K the the Goldreich-Julian current can be supplied thermal emission alone. The surface temperature however has a lower limit in the order of 105 K due to the rotational braking. Therefore, in most cases a sufficient supply of charges for the Goldreich-Julian current is available and the electrical field accelerating the particles will be quenched as a result of their abundance. Otherwise a residual equilibrium electric field Eeq remains with: 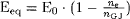 and hence the equilibrium density is: n = nfieid(Eeq, EW) + nDS(Eeq, EW, T) For a temperature just below the onset of thermal emission (T = 1.85 · 105K) the charge density is found to vary almost linearly with the work function EW for values of EW between 0.3 and 2 keV. At the chosen value for EW of 417 eV the residual electric field amounts to only 8.5% of the vacuum value. Even in the residual electric field the particles are rapidly accelerated to relativistic energies balanced by inverse Compton and curvature radiation losses.
and hence the equilibrium density is: n = nfieid(Eeq, EW) + nDS(Eeq, EW, T) For a temperature just below the onset of thermal emission (T = 1.85 · 105K) the charge density is found to vary almost linearly with the work function EW for values of EW between 0.3 and 2 keV. At the chosen value for EW of 417 eV the residual electric field amounts to only 8.5% of the vacuum value. Even in the residual electric field the particles are rapidly accelerated to relativistic energies balanced by inverse Compton and curvature radiation losses.
- Type
- Part 6. Emission and Plasma Theory
- Information
- International Astronomical Union Colloquium , Volume 177: Pulsar Astronomy - 2000 and Beyond , 2000 , pp. 463 - 464
- Copyright
- Copyright © Astronomical Society of the Pacific 2000


