No CrossRef data available.
Article contents
Expressions for Precession Formulae
Published online by Cambridge University Press: 30 March 2016
Extract
In 1976, the IAU recommended for the value of the precession constant 50".290 966 per Julian year and, since 1984, most of the ephemerides have used the formulas of Lieske et al. (1977). In this paper, the motion of the ecliptic was based on Newcomb’s theory. The ecliptic was defined with an accuracy of 0".3 over 1000 years and of 6 mas over one century around J2000. For several years, new determinations of the precession constant have showed that this value is too high by about 3 mas per year. For instance, Williams et al. (1991) give 50".2882 per year. From this value and from the mean elements defining the ecliptic given by Simon et al (1994), we have built new expressions for precession formulae. The motion of the mean ecliptic is described through variables q and p:
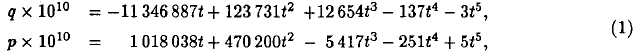 where t is the time reckoned in thousands Julian years from J2000. This solution has an accuracy of 1 mas over several thousands years and 0.1 mas over one century around J2000. The variations of the equator are obtained by integration of the differential equations of the precession in longitude and of the obliquity in Kinoshita (1977) and Kinoshita and Souchay (1990). The dynamical ellipticity is determined in order to obtain (dP/dt) = 50 288".2 at t = 0 as Hd = 0.003 273 7752. From this value for Hd, we can integrate the differential equations for P and ε:
where t is the time reckoned in thousands Julian years from J2000. This solution has an accuracy of 1 mas over several thousands years and 0.1 mas over one century around J2000. The variations of the equator are obtained by integration of the differential equations of the precession in longitude and of the obliquity in Kinoshita (1977) and Kinoshita and Souchay (1990). The dynamical ellipticity is determined in order to obtain (dP/dt) = 50 288".2 at t = 0 as Hd = 0.003 273 7752. From this value for Hd, we can integrate the differential equations for P and ε:
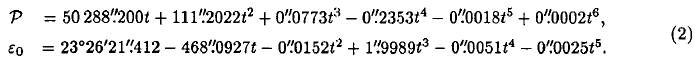
- Type
- II. Joint Discussions
- Information
- Copyright
- Copyright © Kluwer 1995


