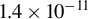1 Introduction
Polarization is one of the fundamental characteristics of electromagnetic radiation[ Reference Maxwell1]. Polarimetry, the quantitative determination of the polarization state, is a multifunctional and sensitive method to study light–matter interaction. In general, a polarimeter consists of two polarizers – called polarizer and analyzer – and their linear polarization transmission directions have an angle to each other, usually using orthogonal polarization settings (refer to Figure 1): a beam from the light source becomes linearly polarized by the polarizer. The linearly polarized light undergoes a change in polarization as it passes through the anisotropic sample. Only the beam component whose polarization meets the transmission direction of the analyzer can finally pass through the analyzer and can be detected by the detector. The physical properties of the sample can be obtained by detecting the change in polarization of the beam before and after it passes through the sample.

Figure 1 Basic scheme of polarimetry. Essential is the pair of polarizers with different and variable orientations to each other to study the effect of a sample in between on the polarization.
Polarimetry with high resolution, which breaks the limitations of low spatial resolution inherent in traditional measurement methods, is an emerging detection tool for atmospheric remote sensing, astronomy, biomedical diagnostics and much more[ Reference Snik, Craven-Jones, Escuti, Fineschi, Harrington, Martino, Mawet, Riedi and Tyo2, Reference Axer, Amunts, Grässel, Palm, Dammers, Axer, Pietrzyk and Zilles3]. For instance, by combining it with multi-spectral and multi-angle functionality, polarimetry allows for the analysis of an aerosol’s microphysical properties and chemical composition in atmospheric remote sensing[ Reference Dubovik, Li, Mishchenko, Tanré, Karol, Bojkov, Cairns, Diner, Espinosa, Goloub, Gu, Hasekamp, Hong, Hou, Knobelspiesse, Landgraf, Li, Litvinov, Liu, Lopatin, Marbach, Maring, Martins, Meijer, Milinevsky, Mukai, Parol, Qiao, Remer, Rietjens, Sano, Stammes, Stamnes, Sun, Tabary, Travis, Waquet, Xu, Yan and Yin4, Reference Chen, Dubovik, Schuster, Chin, Henze, Lapyonok, Li, Derimian and Zhang5]. In biomedical diagnostics, the degree of polarization depends on the properties of the biological tissues. Polarimetry is a diagnostic for tissue properties and provides a useful method for early cancer detection[ Reference Novikova, Pierangelo, Martino, Benali and Validire6].
At the beginning of the 20th century, Barkla[ Reference Barkla7– Reference Barkla9] pointed out that X-rays are polarized. X-ray polarimetry has been developed gradually in many research fields because of the short wavelength and great penetration of X-rays[ Reference Skalicky and Malgrange10, Reference Hart11]. For the detection of magnetic fields, polarized X-rays have the appropriate ability to explore the features of magnetic structures in structural magnetism and the X-ray polarization can discriminate chiral from helimagnetic structures[ Reference Ohsumi and Arima12– Reference Schmitt, Joly, Schulze, Marx-Glowna, Uschmann, Grabiger, Bernhardt, Loetzsch, Juhin, Debray, Wille, Yavaş, Paulus and Röhlsberger15]. In the measurement of X-ray optical activity, Siddons et al.[ Reference Siddons, Hart, Amemiya and Hastings16] successfully observed the optical activity and obtained 2 mrad rotations in a chiral organometallic compound.
Moreover, polarimetry with high sensitivity can be applied to explore the nonlinear properties of a vacuum. In the quantum electrodynamics (QED) description of vacuum[ Reference Heisenberg and Euler17], virtual particle–antiparticle pairs, called quantum fluctuations, are allowed for ultra-short times. In strong external electric or magnetic fields, these virtual particle pairs can be partially aligned, resulting in an optical property of the vacuum.
In essence, fields
![]() $\mathbf{E}$
and
$\mathbf{E}$
and
![]() $\mathbf{B}$
yield higher-order terms of the Lagrangian
$\mathbf{B}$
yield higher-order terms of the Lagrangian
![]() $\mathrm{\mathcal{L}}$
describing the wave propagation[
Reference Ahmadiniaz, Cowan, Sauerbrey, Schramm, Schlenvoigt and Schützhold18–
Reference Gies21], where the first-order correction reads (in natural units
$\mathrm{\mathcal{L}}$
describing the wave propagation[
Reference Ahmadiniaz, Cowan, Sauerbrey, Schramm, Schlenvoigt and Schützhold18–
Reference Gies21], where the first-order correction reads (in natural units
![]() $\mathrm{\hslash}=c=1$
) as follows:
$\mathrm{\hslash}=c=1$
) as follows:
where
![]() $\xi$
is a normalization:
$\xi$
is a normalization:
 $$\begin{align}\xi =\frac{2{\alpha}^2}{45{m}^4}\propto \frac{\alpha }{E_{\mathrm{crit}}^2},\end{align}$$
$$\begin{align}\xi =\frac{2{\alpha}^2}{45{m}^4}\propto \frac{\alpha }{E_{\mathrm{crit}}^2},\end{align}$$
with
![]() $\alpha$
being the fine structure constant,
$\alpha$
being the fine structure constant,
![]() $m$
the particle’s rest mass (constituting the virtual pairs) and
$m$
the particle’s rest mass (constituting the virtual pairs) and
![]() ${E}_{\mathrm{crit}}^2$
the critical field of QED. Considering electrons and positrons as the lightest and therefore most relevant species (due to
${E}_{\mathrm{crit}}^2$
the critical field of QED. Considering electrons and positrons as the lightest and therefore most relevant species (due to
![]() $\propto {m}^{-4}$
-scaling) for quantum fluctuations, the critical field in SI units reads as follows:
$\propto {m}^{-4}$
-scaling) for quantum fluctuations, the critical field in SI units reads as follows:
where
![]() $c$
is the vacuum speed of light. This relation shows the magnitudes the fields must have in order that those effects occur. The nuclei of atoms provide very strong Coulomb fields and lead to specific QED corrections, referred to as the Lamb shift, anomalous magnetic moment and Delbrück scattering[
Reference Furry22–
Reference Milstein and Schumacher28].
$c$
is the vacuum speed of light. This relation shows the magnitudes the fields must have in order that those effects occur. The nuclei of atoms provide very strong Coulomb fields and lead to specific QED corrections, referred to as the Lamb shift, anomalous magnetic moment and Delbrück scattering[
Reference Furry22–
Reference Milstein and Schumacher28].
More attractive to scientists is the case of controllable fields, that is, laboratory vacuum and laboratory fields. The reason for the interest is the dependence on
![]() ${m}^{-4}$
, such that hypothetical light particles would contribute significantly.
${m}^{-4}$
, such that hypothetical light particles would contribute significantly.
Considering two different origins of the fields, a strong background field and a weak probing field, the right-hand part of Equation (1) describes a correction
![]() $\Delta n$
of the refractive index to the classical
$\Delta n$
of the refractive index to the classical
![]() $n=1$
for a vacuum. Yet, depending on the relative k-vector and electric field orientation, there are two components for left- and right-handed circular polarization components of the probe field,
$n=1$
for a vacuum. Yet, depending on the relative k-vector and electric field orientation, there are two components for left- and right-handed circular polarization components of the probe field,
with
![]() $\mathcal{A}$
being a measure of quadratic field strength normalized to the critical field, such as
$\mathcal{A}$
being a measure of quadratic field strength normalized to the critical field, such as
![]() ${\left(E/{E}_{\mathrm{crit}}\right)}^2$
or
${\left(E/{E}_{\mathrm{crit}}\right)}^2$
or
![]() ${\left(B/{B}_{\mathrm{crit}}\right)}^2$
for static fields or
${\left(B/{B}_{\mathrm{crit}}\right)}^2$
for static fields or
![]() $I/{I}_{\mathrm{crit}}$
for a beam intensity
$I/{I}_{\mathrm{crit}}$
for a beam intensity
![]() $I$
(see Section 3).
$I$
(see Section 3).
Hence, the difference of the phase velocities yields a birefringence of the vacuum[
Reference Heisenberg and Euler17–
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19,
Reference Brezin and Itzykson29–
Reference Karbstein36], whereas the difference from
![]() $n=1$
yields a refraction in general. Furthermore, the external field, polarizing the vacuum, can be realized by static fields or by electromagnetic waves. The latter is considered photon-photon or light-by-light scattering[
Reference King and Elkina37,
Reference Hill and Roso38], which would not happen in classical electrodynamics. A good overview of vacuum birefringence is given in a recent review paper[
Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson39] and the references therein.
$n=1$
yields a refraction in general. Furthermore, the external field, polarizing the vacuum, can be realized by static fields or by electromagnetic waves. The latter is considered photon-photon or light-by-light scattering[
Reference King and Elkina37,
Reference Hill and Roso38], which would not happen in classical electrodynamics. A good overview of vacuum birefringence is given in a recent review paper[
Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson39] and the references therein.
So far, vacuum birefringence laboratory experiments have employed linearly polarized optical laser beams in magnetic fields and are reported for PVLAS[
Reference Ataman40,
Reference Ejlli, Valle, Gastaldi, Messineo, Pengo, Ruoso and Zavattini41], BMV[
Reference Agil, Battesti and Rizzo42] and Q&A [
Reference Chen, Mei and Ni43,
Reference Mei, Ni, Chen and Pan44]. Ejlli et al.[
Reference Ejlli, Valle, Gastaldi, Messineo, Pengo, Ruoso and Zavattini41] concluded that the final limits on vacuum magnetic birefringence
![]() $\Delta n$
and dichroism
$\Delta n$
and dichroism
![]() $\Delta \kappa$
of the PVLAS-FE experiment at
$\Delta \kappa$
of the PVLAS-FE experiment at
![]() $B=2.5\ \mathrm{T}\approx 5.7\times {10}^{-10}{B}_{\mathrm{crit}}$
are as follows:
$B=2.5\ \mathrm{T}\approx 5.7\times {10}^{-10}{B}_{\mathrm{crit}}$
are as follows:
 $$\begin{align*} \Delta n=\left(12\pm 17\right)\times {10}^{-23},\\ \Delta \kappa =\left(10\pm 28\right)\times {10}^{-23}.\end{align*}$$
$$\begin{align*} \Delta n=\left(12\pm 17\right)\times {10}^{-23},\\ \Delta \kappa =\left(10\pm 28\right)\times {10}^{-23}.\end{align*}$$
The experiment is compatible with the absence of vacuum birefringence. Agil et al.[ Reference Agil, Battesti and Rizzo42] clarify that the limiting noise affecting the vacuum linear magnetic birefringence experiment is a birefringence one, and expect to get 100 times better results in polarimetry experiments by eliminating the limiting noise in the BMV experiment.
The major challenge of vacuum birefringence experiments is the extremely small effect, where two laboratory quantities may leverage (i) the provision of sufficiently strong external fields by intense radiation and (ii) using a shorter probe wavelength. The former argument is pretty clear when considering Equation (4) and
![]() $\mathcal{A}$
. The latter argument is derived from the phase shift being observable for changes of the refractive index: for a birefringent medium of length
$\mathcal{A}$
. The latter argument is derived from the phase shift being observable for changes of the refractive index: for a birefringent medium of length
![]() $\mathrm{\ell}$
, the accumulated phase shift is
$\mathrm{\ell}$
, the accumulated phase shift is
![]() $\Delta \phi =2\pi \cdot \Delta n\cdot \mathrm{\ell}/\lambda$
, with
$\Delta \phi =2\pi \cdot \Delta n\cdot \mathrm{\ell}/\lambda$
, with
![]() $\lambda$
being the wavelength of the probe beam passing through the birefringent vacuum.
$\lambda$
being the wavelength of the probe beam passing through the birefringent vacuum.
For the above-mentioned studies, the effective path is generated by a Fabry–Pérot setup in meter-long magnetic fields, providing
![]() $\mathrm{\ell}\sim {10}^6\ \mathrm{m}$
while
$\mathrm{\ell}\sim {10}^6\ \mathrm{m}$
while
![]() $\lambda \sim {10}^{-6}\ \mathrm{m}$
, and thus
$\lambda \sim {10}^{-6}\ \mathrm{m}$
, and thus
![]() $\mathrm{\ell}/\lambda \sim {10}^{12}$
. However,
$\mathrm{\ell}/\lambda \sim {10}^{12}$
. However,
![]() $\mathcal{A}\sim {\left({10}^{-10}\right)}^2={10}^{-20}$
. In contrast, schemes proposing an intense laser beam to generate the birefringence and an X-ray beam for probing gain significantly by the field strength but lose in effective interaction length:
$\mathcal{A}\sim {\left({10}^{-10}\right)}^2={10}^{-20}$
. In contrast, schemes proposing an intense laser beam to generate the birefringence and an X-ray beam for probing gain significantly by the field strength but lose in effective interaction length:
![]() $\mathcal{A}=I/{I}_{\mathrm{crit}}\sim {10}^{21}/{10}^{29}\sim {10}^{-8}\ggg {10}^{-20}$
and
$\mathcal{A}=I/{I}_{\mathrm{crit}}\sim {10}^{21}/{10}^{29}\sim {10}^{-8}\ggg {10}^{-20}$
and
![]() $\mathrm{\ell}/\lambda \sim {10}^{-6}\ \mathrm{m}/{10}^{-10}\ \mathrm{m}\sim {10}^4\ll {10}^{12}$
can be estimated. Comparing the schemes, the latter promises a factor of
$\mathrm{\ell}/\lambda \sim {10}^{-6}\ \mathrm{m}/{10}^{-10}\ \mathrm{m}\sim {10}^4\ll {10}^{12}$
can be estimated. Comparing the schemes, the latter promises a factor of
![]() $({10}^{-8}/{10}^{-20})\times ({10}^4/{10}^{12})\sim {10}^4$
more phase shift than the current laboratory experiments.
$({10}^{-8}/{10}^{-20})\times ({10}^4/{10}^{12})\sim {10}^4$
more phase shift than the current laboratory experiments.
This stimulated scientists to improve the performance of X-ray polarimetry. Here, we review the related studies. In this paper, the contents are as follows. We introduce X-ray polarimetry in Section 2. First of all, we discuss the polarization purity of X-rays and the influencing factors and limitations in Section 2.1, followed by details for a high-quality X-ray polarizer in Section 2.2. In Section 3, we present the details of detecting vacuum birefringence, including experimental setups (Section 3.2) and general signal estimates (Section 3.3). We further discuss available facilities (Section 3.4) and related instrumentation (Section 3.4.4). Section 4 provides a brief description of the applications of X-ray polarimetry to nuclear resonant scattering, strong-field physics and astrophysics.

Figure 2 Basic diffraction geometry for anomalous transmission of X-rays (Borrmann effect). Reprinted from Ref. [Reference Cole, Chambers and Wood45], with the permission of AIP Publishing.
2 X-ray polarimetry
The basic schematic shown in Figure 1 can be transferred to the X-ray domain, such that polarizing elements are required for the roles of polarizer and analyzer. Here we discuss the crucial components and potential accuracy of X-ray polarimetry. First, we would like to introduce two methods to obtain polarized X-rays.
The Borrmann effect, or anomalous transmission, was discovered by Borrmann[
Reference Borrmannn46] in 1941. Polarized X-rays are produced when X-rays pass through crystals because of the different absorbance of two orthogonal polarization planes[
Reference Cole, Chambers and Wood45,
Reference Batterman and Cole47]. The polarization state with the electric vector in the plane of incidence is preferentially absorbed, in comparison to the polarization state with the electric vector perpendicular to the plane of incidence. Here, polarizers based on the Borrmann effect are applied to the investigation of the electric-magnetic properties of ferroelectric materials and optical properties in chiral compounds[
Reference Siddons, Hart, Amemiya and Hastings16,
Reference Schulze, Marx, Uschmann, Förster, Stöhlker and Paulus48]. The drawbacks of this polarizer are the low efficiency and a narrow angular acceptance[
Reference Mills49]. In 1961, Cole et al.[
Reference Cole, Chambers and Wood45] constructed a polarizer-monochromator, where the polarizer is made from a single germanium crystal slab with 1 mm thickness, and the diffracted beam based on the Borrmann effect is polarized, as shown in Figure 2. The best intensity ratio of the two orthogonal polarization states based on the Borrmann effect is less than
![]() $1.5\times {10}^{-5}$
for a 2 mm thick silicon crystal polarizer and a 4 mm thick analyzer[
Reference Schulze, Marx, Uschmann, Förster, Stöhlker and Paulus48].
$1.5\times {10}^{-5}$
for a 2 mm thick silicon crystal polarizer and a 4 mm thick analyzer[
Reference Schulze, Marx, Uschmann, Förster, Stöhlker and Paulus48].
Alternatively, polarized X-rays can be produced on perfect crystals with the Bragg diffraction at nearly 45° and thereby exploiting Brewster’s law[
Reference Skalicky and Malgrange10,
Reference Muleri, Soffitta, Bellazzini, Brez, Costa, Frutti, Mastropietro, Morelli, Pinchera, Rubini and Spandre50]. As shown in Figure 3, the Bragg diffraction happens near the crystal surface for low absorption. The polarization component parallel to the plane of diffraction (
![]() $\parallel$
state or
$\parallel$
state or
![]() $\pi$
or p-polarization state) disappears due to Brewster’s law, but the vertical polarization component (
$\pi$
or p-polarization state) disappears due to Brewster’s law, but the vertical polarization component (
![]() $\perp$
state or
$\perp$
state or
![]() $\sigma$
or s-polarization state) remains. In this way, linearly polarized X-rays are generated. Disadvantages are the requirement of a Bragg angle of exactly 45° and the limitation of wavelengths due to materials.
$\sigma$
or s-polarization state) remains. In this way, linearly polarized X-rays are generated. Disadvantages are the requirement of a Bragg angle of exactly 45° and the limitation of wavelengths due to materials.

Figure 3 Geometry of the Bragg diffraction at 45°. Unpolarized radiation is polarized because the
![]() $\pi$
-component, being in the plane of incidence, is not allowed for reflection (Brewster’s law). Used with the permission of SPIE, from Ref. [Reference Muleri, Soffitta, Bellazzini, Brez, Costa, Frutti, Mastropietro, Morelli, Pinchera, Rubini and Spandre50]; permission conveyed through Copyright Clearance Center, Inc.
$\pi$
-component, being in the plane of incidence, is not allowed for reflection (Brewster’s law). Used with the permission of SPIE, from Ref. [Reference Muleri, Soffitta, Bellazzini, Brez, Costa, Frutti, Mastropietro, Morelli, Pinchera, Rubini and Spandre50]; permission conveyed through Copyright Clearance Center, Inc.
2.1 Polarization purity
Here we discuss the generation of pure linear polarization states of X-rays based on Bragg diffraction at perfect crystals[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51–
Reference Hart and Rodrigues54]. The polarization purity
![]() $\mathcal{P}$
is defined as the intensity ratio of the (suppressed) polarization
$\mathcal{P}$
is defined as the intensity ratio of the (suppressed) polarization
![]() $\pi$
-component to the
$\pi$
-component to the
![]() $\sigma$
-component, as shown in Figure 3, and then integrated over angle
$\sigma$
-component, as shown in Figure 3, and then integrated over angle
![]() $\theta$
and wavelength
$\theta$
and wavelength
![]() $\lambda$
ranges[
Reference Schulze52,
Reference Hart and Rodrigues54]:
$\lambda$
ranges[
Reference Schulze52,
Reference Hart and Rodrigues54]:
 $$\begin{align}\mathcal{P}=\frac{\int \int {I}_{\pi}\left(\lambda, \theta \right)\kern0.1em \mathrm{d}\lambda \kern0.1em \mathrm{d}\theta }{\int \int {I}_{\sigma}\left(\lambda, \theta \right)\kern0.1em \mathrm{d}\lambda \kern0.1em \mathrm{d}\theta }.\end{align}$$
$$\begin{align}\mathcal{P}=\frac{\int \int {I}_{\pi}\left(\lambda, \theta \right)\kern0.1em \mathrm{d}\lambda \kern0.1em \mathrm{d}\theta }{\int \int {I}_{\sigma}\left(\lambda, \theta \right)\kern0.1em \mathrm{d}\lambda \kern0.1em \mathrm{d}\theta }.\end{align}$$
Obviously
![]() $0<\mathcal{P}\le 1$
, and a high degree of linear polarization means
$0<\mathcal{P}\le 1$
, and a high degree of linear polarization means
![]() $\mathcal{P}\ll 1$
. Thus,
$\mathcal{P}\ll 1$
. Thus,
![]() $\mathcal{P}$
is a measure of relative impurity. On the other hand, for a perfectly polarized source with
$\mathcal{P}$
is a measure of relative impurity. On the other hand, for a perfectly polarized source with
![]() $N$
photons and a polarization-independent transmission
$N$
photons and a polarization-independent transmission
![]() $T$
of the polarizer,
$T$
of the polarizer,
![]() $NT\mathcal{P}$
photons are transmitted in a crossed polarizer setting.
$NT\mathcal{P}$
photons are transmitted in a crossed polarizer setting.
The intensity ratio of the polarization components
![]() $\sigma$
to
$\sigma$
to
![]() $\pi$
is related with the angle-integrated reflectivity of two polarization states,
$\pi$
is related with the angle-integrated reflectivity of two polarization states,
![]() ${R}_{\sigma }$
and
${R}_{\sigma }$
and
![]() ${R}_{\pi }$
, as follows:
${R}_{\pi }$
, as follows:
 $$\begin{align}\frac{I_{\pi }}{I_{\sigma }}=\frac{\int {R}_{\pi}\left(\theta \right)\kern0.2em \mathrm{d}\theta }{\int {R}_{\sigma}\left(\theta \right)\kern0.2em \mathrm{d}\theta}.\end{align}$$
$$\begin{align}\frac{I_{\pi }}{I_{\sigma }}=\frac{\int {R}_{\pi}\left(\theta \right)\kern0.2em \mathrm{d}\theta }{\int {R}_{\sigma}\left(\theta \right)\kern0.2em \mathrm{d}\theta}.\end{align}$$
In the following, we discuss the requirements and limitations of extremely high purities
![]() $\mathcal{P}\ll 1$
.
$\mathcal{P}\ll 1$
.
2.1.1 Beam divergence
As very simple geometric effect, a beam divergence leads to a deviation from a Bragg angle of exactly 45° for some parts of a beam, impinging on a perfect crystal, and thus a minor contribution in the
![]() $\pi$
-polarized component[
Reference Schulze52]. Assuming the X-ray beam is a Gaussian beam, the relationship between the divergence and the polarization purity is as follows[
Reference Schulze52,
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55]:
$\pi$
-polarized component[
Reference Schulze52]. Assuming the X-ray beam is a Gaussian beam, the relationship between the divergence and the polarization purity is as follows[
Reference Schulze52,
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55]:
with
![]() ${\sigma}_{\mathrm{V}}$
and
${\sigma}_{\mathrm{V}}$
and
![]() ${\sigma}_{\mathrm{H}}$
being the divergence in the vertical and horizontal direction, respectively.
${\sigma}_{\mathrm{H}}$
being the divergence in the vertical and horizontal direction, respectively.
In 2020, Bernhardt et al.[
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] experimentally verified Schulze’s[
Reference Schulze52] theoretical analysis by studying the effect of beam horizontal divergence on X-ray polarization purity at beamline ID18 of the European Synchrotron Radiation Facility (ESRF). The comparison of the X-ray polarization purity between the fitted data (
![]() ${\mathcal{P}}_{\mathrm{exp}}$
) and the calculated data (
${\mathcal{P}}_{\mathrm{exp}}$
) and the calculated data (
![]() ${\mathcal{P}}_{\mathrm{Divergence}}^{\mathrm{Limit}}$
, using Equation (7)) is presented in Table 1. The polarization purity from the fitted data points and the calculated limit match very well for all three horizontal beam divergences. When the horizontal divergence of X-ray was reduced from 17 to 8.4 μrad by a slit with variable gap and a V-shaped channel-cut (VCC), the X-ray polarization purity decreased to
${\mathcal{P}}_{\mathrm{Divergence}}^{\mathrm{Limit}}$
, using Equation (7)) is presented in Table 1. The polarization purity from the fitted data points and the calculated limit match very well for all three horizontal beam divergences. When the horizontal divergence of X-ray was reduced from 17 to 8.4 μrad by a slit with variable gap and a V-shaped channel-cut (VCC), the X-ray polarization purity decreased to
![]() $1.4\times {10}^{-10}$
[
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55]. In addition, this paper and others[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19,
Reference Tschentscher, Bressler, Grünert, Madsen, Mancuso, Meyer, Scherz, Sinn and Zastrau56] mention that 1 μrad divergence is available for the X-ray free electron laser (XFEL). Therefore, the X-ray polarization purity is limited to the order of
$1.4\times {10}^{-10}$
[
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55]. In addition, this paper and others[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19,
Reference Tschentscher, Bressler, Grünert, Madsen, Mancuso, Meyer, Scherz, Sinn and Zastrau56] mention that 1 μrad divergence is available for the X-ray free electron laser (XFEL). Therefore, the X-ray polarization purity is limited to the order of
![]() ${10}^{-12}$
.
${10}^{-12}$
.
Table 1 Comparison of measured purity
![]() ${\mathcal{P}}_{\mathrm{exp}}$
against the calculated limit
${\mathcal{P}}_{\mathrm{exp}}$
against the calculated limit
![]() ${\mathcal{P}}_{\mathrm{Divergence}}^{\mathrm{Limit}}$
given by the beam divergence
${\mathcal{P}}_{\mathrm{Divergence}}^{\mathrm{Limit}}$
given by the beam divergence
![]() ${\sigma}_{\mathrm{H}}$
for
${\sigma}_{\mathrm{H}}$
for
![]() ${\sigma}_{\mathrm{V}}=6.1\;\unicode{x3bc} \mathrm{rad}$
. Taken from Ref. [Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55], licensed under CC BY 4.0.
${\sigma}_{\mathrm{V}}=6.1\;\unicode{x3bc} \mathrm{rad}$
. Taken from Ref. [Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55], licensed under CC BY 4.0.

2.1.2 Crystal quality
Crystal quality affects the polarization purity in two ways. First, for similar geometric reasons to the divergence, all parts of a (perfectly parallel) beam of finite size must experience the same 45° incidence angle to allow for the same polarization suppression[ Reference Hart and Rodrigues54]. Second, imperfect crystals have varying lattice constants that affect the reflectivity curves and thus the spectral/angular acceptance and integrated reflectivity. Thus, the properties of the crystal material must be taken into account to avoid the depolarization of X-rays.
Researchers[ Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53, Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] have used artificial diamonds containing a mass of crystalline defects produced by chemical vapor deposition (CVD) as a polarizer in X-ray polarimetry. Contrary to expectations and the prediction of Hart and Rodrigues[ Reference Hart and Rodrigues54], imperfections of artificial diamonds have no observable influence on the polarization purity of X-rays but lead to low peak reflectivity and low transmittance of polarizers[ Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55]. Furthermore, polarimetry at photon energies above 10 keV can benefit from imperfections because of the higher integrated reflectivity. For low photon energies, the nearly perfect crystals with high reflectivity are essential for the expected highly linearly polarized X-rays[ Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55].
2.1.3 Detour reflections (Umweganregungen)
Another limitation of the polarization purity is detour reflections (Umweganregung)[ Reference Renninger57]. These are the result of consecutive Bragg diffractions on different lattice planes and therefore different Bragg angles, yielding in sequence the same beam reflection angle as the primary reflection. This is similar to a cat’s-eye retro-reflector, where the rays bounce off several surfaces, in contrast to a mirror where only one reflection occurs. In fact, the detours are only possible in 3D crystals due to the abundance of lattice planes in directions off the main reflection.
As a result, every partial Bragg diffraction does not happen with a 45° Bragg angle such that the Brewster condition is not fulfilled, and no strong ratios of
![]() ${R}_{\pi }:{R}_{\sigma }$
are yielded, even in sequence. Yet, the overall intensity can be relatively weak compared to the beam from the 45° (main) Bragg diffraction. Still, these unpolarized contributions yield a limit for the polarization purity.
${R}_{\pi }:{R}_{\sigma }$
are yielded, even in sequence. Yet, the overall intensity can be relatively weak compared to the beam from the 45° (main) Bragg diffraction. Still, these unpolarized contributions yield a limit for the polarization purity.
The Ewald sphere is a geometric construction to determine the diffraction direction of crystals, and diffraction will occur only for reciprocal lattice points that lie on the surface of the Ewald sphere. The consecutive reflections case happens at nearby lattice planes in 3D crystals if there are more than two reciprocal lattice points that lie on the Ewald sphere. Under some azimuth angles, the incident beam excites not only the required intended reflection with a 45° Bragg angle but also secondary reflections – not with a 45° Bragg angle. As a result, the latter reflections will cause the depolarization of X-rays when the secondary, detoured reflections exit into the same exit direction of the principal reflection[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51,
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53,
Reference Renninger57], and the polarization purity is suppressed. Marx et al.[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51] provided the reflection system for a silicon crystal and an X-ray energy of 12.914 keV, as shown in Figure 4. The radius of the Ewald sphere is
![]() $1/\lambda$
, where
$1/\lambda$
, where
![]() $\lambda$
is the wavelength of the incident beam. The intersections of the colored lines are the multi-beam cases. The effect of multi-beam situations can be reduced by optimizing the crystal azimuth to avoid the excitation of secondary reflections[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53]. In addition, using lower photon energies reduces the size of the Ewald sphere and therefore reduces the number of potential detour cases.
$\lambda$
is the wavelength of the incident beam. The intersections of the colored lines are the multi-beam cases. The effect of multi-beam situations can be reduced by optimizing the crystal azimuth to avoid the excitation of secondary reflections[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53]. In addition, using lower photon energies reduces the size of the Ewald sphere and therefore reduces the number of potential detour cases.

Figure 4 Kossel pattern of silicon at 12.914 keV. The bold black circle represents the exploited Si (800) reflection used for suppression of the component. All other possible reflections are depicted by thin colored circles. The vectors
![]() ${\overrightarrow{S}}_0$
and
${\overrightarrow{S}}_0$
and
![]() ${\overrightarrow{S}}_{\mathrm{h}}$
describe the direction of the incident and diffracted wave, respectively. In order to avoid degradation of the polarization purity due to multiple-beam cases, the azimuth has to be chosen such that the ‘distance’ to the closest undesired reflections is as large as possible. Reprinted from Ref. [Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51], with the permission of APS.
${\overrightarrow{S}}_{\mathrm{h}}$
describe the direction of the incident and diffracted wave, respectively. In order to avoid degradation of the polarization purity due to multiple-beam cases, the azimuth has to be chosen such that the ‘distance’ to the closest undesired reflections is as large as possible. Reprinted from Ref. [Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51], with the permission of APS.
2.1.4 Material dependence
It is obvious from the previous sections that the material has a strong influence, mainly to provide crystals of the highest quality (cf. Section 2.1.2). At present, Si (
![]() $Z=14$
)[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51,
Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus58–
Reference Marx-Glowna, Schulze, Uschmann, Kämpfer, Weber, Hahn, Wille, Schlage, Röhlsberger, Förster, Stöhlker and Paulus60] and diamond (
$Z=14$
)[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51,
Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus58–
Reference Marx-Glowna, Schulze, Uschmann, Kämpfer, Weber, Hahn, Wille, Schlage, Röhlsberger, Förster, Stöhlker and Paulus60] and diamond (
![]() $Z=6$
)[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53,
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] are widely available. Ge (
$Z=6$
)[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53,
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] are widely available. Ge (
![]() $Z=32$
)[
Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61] exhibits a reflection for Cu X-ray tubes but is abandoned gradually. Silicon crystals with a perfect crystal structure, few impurities and a very mature preparation technology are adopted widely as polarizers.
$Z=32$
)[
Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61] exhibits a reflection for Cu X-ray tubes but is abandoned gradually. Silicon crystals with a perfect crystal structure, few impurities and a very mature preparation technology are adopted widely as polarizers.
For silicon and diamond, Bernhardt et al.[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53] compared the reflectivity of those two materials for the Bragg reflection at a 45° angle, as illustrated in Figure 5. The solid line and dashed line are the reflectivity curves of diamond and silicon, respectively. The curve for diamond is higher but narrower than that for silicon. This is a quite general behavior[
Reference Als-Nielsen and McMorrow62] and the reason lies mainly in the number of electrons per atom,
![]() $Z$
. Silicon has more electrons, and thus scatters more intensity per lattice plane and fewer lattice planes are needed for Bragg reflection. This explains the wider spectral/angular width of the curve. On the other hand, the absorption per atom of silicon is higher, and thus the peak reflectivity is not as high as for diamond. The photon energy
$Z$
. Silicon has more electrons, and thus scatters more intensity per lattice plane and fewer lattice planes are needed for Bragg reflection. This explains the wider spectral/angular width of the curve. On the other hand, the absorption per atom of silicon is higher, and thus the peak reflectivity is not as high as for diamond. The photon energy
![]() ${E}_{\mathrm{ph}}$
also plays a role here, as diamond has a smaller unit cell and thus the wavelength for the same (400) reflection is shorter. With higher photon energy, absorption reduces and penetration increases; hence, this also contributes to the narrower and higher curve of diamond.
${E}_{\mathrm{ph}}$
also plays a role here, as diamond has a smaller unit cell and thus the wavelength for the same (400) reflection is shorter. With higher photon energy, absorption reduces and penetration increases; hence, this also contributes to the narrower and higher curve of diamond.

Figure 5 Reflectivity of X-rays for the
![]() $\sigma$
–polarization in 45° symmetric Bragg scattering geometry as a function of the angle of incidence, according to dynamical theory calculations. Solid line: the (400) Bragg reflection in diamond for 9.831 keV. Dashed line: the (400) Bragg reflection in silicon for 6.457 keV, as used by Marx et al.[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51]. Note that
$\sigma$
–polarization in 45° symmetric Bragg scattering geometry as a function of the angle of incidence, according to dynamical theory calculations. Solid line: the (400) Bragg reflection in diamond for 9.831 keV. Dashed line: the (400) Bragg reflection in silicon for 6.457 keV, as used by Marx et al.[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51]. Note that
![]() ${1}^{"}\approx 5\;\unicode{x3bc} \mathrm{rad}$
. Reprinted from Ref. [Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53], with the permission of AIP Publishing.
${1}^{"}\approx 5\;\unicode{x3bc} \mathrm{rad}$
. Reprinted from Ref. [Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53], with the permission of AIP Publishing.
For applications, however, the integrated reflectivity can be of interest, for example, if the beam has a finite spectral bandwidth or divergence. The integrated reflectivity of diamond is much smaller than that of silicon. For example, a later work by Bernhardt et al.[ Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] used diamonds with many crystalline defects and showed a peak reflectivity of only 50%–60%, while the rocking curve broadened by a factor of approximately 2.
There is also a material dependence of detour reflections. Tischler and Batterman[ Reference Tischler and Batterman63] provided that the resulting contribution of all reflections is dependent on the amplitude for each detour:
 $$\begin{align}{E}_{\mathrm{mult}}=\sum \limits_{i=1}^N{E}_i.\end{align}$$
$$\begin{align}{E}_{\mathrm{mult}}=\sum \limits_{i=1}^N{E}_i.\end{align}$$
Based on Equation (8), they calculated the
![]() $N$
-beam integrated intensities for the (622) reflection of germanium (Ge) and silicon (Si). The ratio of intensities is very close to the ratio of atomic numbers to the fourth power[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51,
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55,
Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus58,
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59]:
$N$
-beam integrated intensities for the (622) reflection of germanium (Ge) and silicon (Si). The ratio of intensities is very close to the ratio of atomic numbers to the fourth power[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51,
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55,
Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus58,
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59]:
 $$\begin{align*}{\left(\frac{E_{\mathrm{mult}}^{\mathrm{Ge}}}{E_{\mathrm{mult}}^{\mathrm{Si}}}\right)}^2={\left(\frac{0.038}{0.0075}\right)}^2\simeq 25.7\approx {\left(\frac{Z_{\mathrm{Ge}}}{Z\mathrm{Si}}\right)}^4=\left(\frac{32}{14}\right)\simeq 27.3.\end{align*}$$
$$\begin{align*}{\left(\frac{E_{\mathrm{mult}}^{\mathrm{Ge}}}{E_{\mathrm{mult}}^{\mathrm{Si}}}\right)}^2={\left(\frac{0.038}{0.0075}\right)}^2\simeq 25.7\approx {\left(\frac{Z_{\mathrm{Ge}}}{Z\mathrm{Si}}\right)}^4=\left(\frac{32}{14}\right)\simeq 27.3.\end{align*}$$

Figure 6 Schematic of a channel-cut polarizer with
![]() $2\times 2$
reflections. Thin lines indicate the lattice planes for the 45° Bragg reflection, which are parallel to the surface in this case.
$2\times 2$
reflections. Thin lines indicate the lattice planes for the 45° Bragg reflection, which are parallel to the surface in this case.
Consequently, polarizers made by materials with low Z values are favorable to further mitigate the impact of detour reflections, apart from choosing a good azimuth angle.
2.2 Channel-cut precision X-ray polarizers
The significant optical element in X-ray polarimetry for high polarization purity is the polarizer. In 1978 and 1979, respectively, Hart[ Reference Hart11] and Hart and Rodrigues[ Reference Hart and Rodrigues54] established X-ray polarimetry with two-fold Bragg-reflecting channel-cut germanium (Ge) crystals and pointed out that polarization with multiple Bragg reflections has been demonstrated for any X-ray wavelength by using offset grooved crystals. Figure 6 displays a channel-cut polarizer with four reflections at a 45° Bragg angle.
As can be seen in Figure 6, the polarizer consists of two opposing Bragg crystals for a 45° Bragg angle. For simplicity and convenience, the two surfaces are made from a single crystal with a groove or channel cut into it. Thereby, the two surfaces have naturally parallel lattice planes. With appropriate geometry, an even number of reflections can be obtained, maintaining the beam direction while improving the purity (see Section 2.2.1 below). The resulting parallel offset of the beam is a minor problem. The main advantage is the inherent parallelism of both (opposing) lattice planes, such that the Bragg angle is to be aligned only once for all occurring reflections.

Figure 7 Polarization ratios for m-fold multiple Bragg reflection polarizers using the Ge (440) Bragg reflection. Reprinted from Ref. [Reference Hart and Rodrigues54], with the permission of Taylor & Francis.
One method to machine grooves is lapping by low-damage blades of a crystal saw. Alternatively, etching technologies are also excellent to create near-perfect inner channel surfaces to avoid distortions of the X-ray wavefront[ Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus58, Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59]. Channel-cut crystals have been extensively used[ Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51– Reference Hart and Rodrigues54, Reference Bonse and Hart64]. As early as 1965, Bonse and Hart[ Reference Bonse and Hart64] pointed out that the pairs of perfect crystals with a groove cut (Figure 6) obviously reduced the tails caused by the multiple reflections. In 1978, Hart[ Reference Hart11] constructed an X-ray polarimeter with two-fold Bragg-reflecting channel-cut germanium crystals to generate elliptically polarized X-rays. Hart used a mixture of nitric acid and hydrofluoric acid to polish the channel-cut crystals and eliminate the strains introduced in the cutting process. For channel-cut crystals designs, Marx-Glowna et al.[ Reference Marx-Glowna, Schulze, Uschmann, Kämpfer, Weber, Hahn, Wille, Schlage, Röhlsberger, Förster, Stöhlker and Paulus60] pointed out that the calculation of the beam path of Compton scattered photons and the orientation of the crystal should be considered, which affect the polarization purity of X-rays.
2.2.1 Consecutive reflections
It is well known that a polarized light beam can be produced by several transmissions through a number of glass plates, even though each plate is only a partial polarizer. Similarly, channel-cut crystals improve the polarization purity[ Reference Hart and Rodrigues54, Reference DuMond65] since they stack a number of reflections into a single optical element.
Regarding multiple successive Bragg reflections between the walls of a channel cut in an ideal crystal to increase the polarization purity of X-rays, the ratio of intensities of two polarization states for X-rays polarized by
![]() $m$
consecutive Bragg reflections is given by the following[
Reference Alp, Sturhahn and Toellner66]:
$m$
consecutive Bragg reflections is given by the following[
Reference Alp, Sturhahn and Toellner66]:
 $$\begin{align}\frac{I_{\pi }}{I_{\sigma }}=\frac{\int {R}_{\pi}^m\left(\theta \right)\kern0.1em \mathrm{d}\theta }{\int {R}_{\sigma}^m\left(\theta \right)\kern0.1em \mathrm{d}\theta },\end{align}$$
$$\begin{align}\frac{I_{\pi }}{I_{\sigma }}=\frac{\int {R}_{\pi}^m\left(\theta \right)\kern0.1em \mathrm{d}\theta }{\int {R}_{\sigma}^m\left(\theta \right)\kern0.1em \mathrm{d}\theta },\end{align}$$
with the notation of Equation (6). Hart and Rodrigues[
Reference Hart and Rodrigues54] calculated the ratio of
![]() ${I}_{\pi }:{I}_{\sigma }$
for multiple Bragg reflections in a grooved Ge polarizer using two-beam dynamical theory, as shown in Figure 7. The polarization purity decreases as the number of multiple Bragg reflections increases. In 1965, Bonse and Hart[
Reference Bonse and Hart64] found that multiple Bragg reflections between the walls of a channel-cut perfect crystal do not narrow the reflection curves considerably.
${I}_{\pi }:{I}_{\sigma }$
for multiple Bragg reflections in a grooved Ge polarizer using two-beam dynamical theory, as shown in Figure 7. The polarization purity decreases as the number of multiple Bragg reflections increases. In 1965, Bonse and Hart[
Reference Bonse and Hart64] found that multiple Bragg reflections between the walls of a channel-cut perfect crystal do not narrow the reflection curves considerably.
Recently, high polarization purity of X-rays was achieved by multiple reflections. In 2011, Marx et al.[
Reference Marx, Uschmann, Höfer, Lötzsch, Wehrhan, Förster, Kaluza, Stöhlker, Gies, Detlefs, Roth, Härtwig and Paulus58] reported that the highest purity of polarization of X-rays reaches
![]() $1.5\times {10}^{-9}$
based on
$1.5\times {10}^{-9}$
based on
![]() $m=4$
reflections at Si (400) channel-cut crystals for 6 keV X-ray energy. Two years later[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51], they obtained
$m=4$
reflections at Si (400) channel-cut crystals for 6 keV X-ray energy. Two years later[
Reference Marx, Schulze, Uschmann, Kämpfer, Lötzsch, Wehrhan, Wagner, Detlefs, Roth, Härtwig, Förster, Stöhlker and Paulus51], they obtained
![]() $2.4\times {10}^{-10}$
polarization purity of the X-ray using
$2.4\times {10}^{-10}$
polarization purity of the X-ray using
![]() $m=6$
reflections. Here, the energy of the X-ray is 6 keV and the polarizer is Si (400) channel-cut crystals, the same as before.
$m=6$
reflections. Here, the energy of the X-ray is 6 keV and the polarizer is Si (400) channel-cut crystals, the same as before.
2.2.2 Asymmetric cuts
The channel-cut crystals enhance the polarization purity of X-rays. However, the angular and spectral acceptance of channel-cut crystals tends to restrict the throughput of X-rays. To increase the acceptance of channel-cut crystals while maintaining the polarization filtering, researchers[
Reference Alp, Sturhahn and Toellner66–
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68] came up with asymmetrically cut crystals with an asymmetry angle
![]() ${\alpha}_{\mathrm{c}}$
between the lattice planes and the surface. To quantify the asymmetry, the asymmetry parameter
${\alpha}_{\mathrm{c}}$
between the lattice planes and the surface. To quantify the asymmetry, the asymmetry parameter
![]() $b$
for a Bragg diffraction is defined[
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68] by the following:
$b$
for a Bragg diffraction is defined[
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68] by the following:
Note that the asymmetry angle
![]() ${\alpha}_{\mathrm{c}}$
is negative if the incidence angle relative to the crystal surface is smaller than exit angle, as for the first reflection shown in Figure 8.
${\alpha}_{\mathrm{c}}$
is negative if the incidence angle relative to the crystal surface is smaller than exit angle, as for the first reflection shown in Figure 8.

Figure 8 The geometry for an asymmetrically cut channel-cut crystal with a Bragg angle near 45°. The lattice planes, as indicated in Figure 6, are oriented 45° to the beam, yet the crystal surface is slanted. The asymmetry angle
![]() ${\alpha}_{\mathrm{c}}$
is the angle between surface and lattice planes. It is negative for the case shown at the first surface where the incident beam is shallow and leaves with a larger diameter.
${\alpha}_{\mathrm{c}}$
is the angle between surface and lattice planes. It is negative for the case shown at the first surface where the incident beam is shallow and leaves with a larger diameter.
The angular acceptance of the crystal varies with the asymmetry angle as follows:
with
![]() ${\left(\Delta \theta \right)}_{\mathrm{symm}}$
being the usual acceptance from a symmetric reflection.
${\left(\Delta \theta \right)}_{\mathrm{symm}}$
being the usual acceptance from a symmetric reflection.

Figure 9 The effect of an asymmetric cutting angle on both the angular acceptance and the resulting polarization suppression for a silicon (840) channel-cut crystal. Reprinted from Ref. [Reference Toellner, Alp, Sturhahn, Mooney, Zhang, Ando, Yoda and Kikuta67], with the permission of AIP Publishing.
Figure 9 displays the effects of the asymmetry angle on angular acceptance and polarization suppression[ Reference Toellner, Alp, Sturhahn, Mooney, Zhang, Ando, Yoda and Kikuta67]. The angular acceptance increases while the polarization suppression factor decreases when the asymmetry angle approaches 45°. However, a larger asymmetry angle requires larger crystals due to the beam footprint, imposing practical issues.
An overview of the calculated polarization purities of X-rays for different asymmetry angles
![]() ${\alpha}_{\mathrm{c}}$
and different numbers of channel-cut reflections
${\alpha}_{\mathrm{c}}$
and different numbers of channel-cut reflections
![]() $m$
is listed in Table 2 with an explanation of each parameter by annotations. For the same number of reflections, the polarization purity at an asymmetry angle of
$m$
is listed in Table 2 with an explanation of each parameter by annotations. For the same number of reflections, the polarization purity at an asymmetry angle of
![]() $-{28}^{\circ }$
is better than that at an asymmetry angle of
$-{28}^{\circ }$
is better than that at an asymmetry angle of
![]() $-{43}^{\circ }$
. In their paper, Marx-Glowna et al. [
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68] chose a
$-{43}^{\circ }$
. In their paper, Marx-Glowna et al. [
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68] chose a
![]() $-{28}^{\circ }$
asymmetry angle and four reflections because of the practical limitation of the crystal size and preparation (high-quality surface), and obtained experimentally
$-{28}^{\circ }$
asymmetry angle and four reflections because of the practical limitation of the crystal size and preparation (high-quality surface), and obtained experimentally
![]() $\left(2.2\pm 2.0\right)\,{\times}\, {10}^{-9}$
polarization purity finally.
$\left(2.2\pm 2.0\right)\,{\times}\, {10}^{-9}$
polarization purity finally.
Table 2 Calculated polarization purity
![]() $\mathcal{P}$
for asymmetry angle
$\mathcal{P}$
for asymmetry angle
![]() ${\alpha}_{\mathrm{c}}$
and number of reflections
${\alpha}_{\mathrm{c}}$
and number of reflections
![]() $n$
. Here,
$n$
. Here,
![]() ${D}_{-}$
is the accepted beam divergence,
${D}_{-}$
is the accepted beam divergence,
![]() ${S}_{+}$
is the beam footprint on the crystal surface and
${S}_{+}$
is the beam footprint on the crystal surface and
![]() $I/{I}_0$
is the peak reflectivity. Taken from Ref. [Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68], licensed under CC BY 4.0.
$I/{I}_0$
is the peak reflectivity. Taken from Ref. [Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68], licensed under CC BY 4.0.

2.2.3 Quasi-channel-cuts
It may be necessary to realize the two opposing surfaces by two separate crystals. This is called a quasi-channel-cut. It may help to tune the Bragg reflections separately by an angle offset[
Reference Hart and Rodrigues54] since the reflectivity curves for both polarizations
![]() ${R}_{\sigma }$
and
${R}_{\sigma }$
and
![]() ${R}_{\pi }$
can have different widths and positions in an angle.
${R}_{\pi }$
can have different widths and positions in an angle.
Furthermore, not all materials can be grown as large bulk as is done for silicon. For example, diamond is quite attractive because of its high thermal conductivity and low absorption in the X-ray region[
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55], but it is very challenging to produce at large sizes and to obtain high-quality diamond with few dislocations and stacking faults. A reflectivity as high as 99% of hard X-rays from nearly defect-free diamond crystals at near-normal incidence has been reported[
Reference Shvyd’ko, Stoupin, Blank and Terentyev69]. Nevertheless, low crystal quality and complicated production processes constrain the development of diamond in polarizers. Polarization purities of
![]() $8.9\times {10}^{-10}$
[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53] and
$8.9\times {10}^{-10}$
[
Reference Bernhardt, Marx-Glowna, Schulze, Grabiger, Haber, Detlefs, Loetzsch, Kämpfer, Röhlsberger, Förster, Stöhlker, Uschmann and Paulus53] and
![]() ${3\times {10}^{-10}}$
[
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] are reported for using artificial diamond crystals manufactured by CVD.
${3\times {10}^{-10}}$
[
Reference Bernhardt, Schmitt, Grabiger, Marx-Glowna, Loetzsch, Wille, Bessas, Chumakov, Rüffer, Röhlsberger, Stöhlker, Uschmann, Paulus and Schulze55] are reported for using artificial diamond crystals manufactured by CVD.
The setup of a quasi-channel-cut is technically challenging in providing sufficient angular stability of both surfaces.
2.2.4 Temporal effects
Another feature, relevant for applications at XFELs in particular, is the inherent pulse stretching effect for Bragg crystals[
Reference Shvyd’ko and Lindberg70,
Reference Hrdý71]. Due to the scattering at the lattice planes happening over many lattice planes (leading to the finite spectral bandwidth), a short X-ray pulse will become temporally stretched. The ray will enter the crystal at a certain depth where it is effectively diffracted out, being the Bragg-case extinction depth
![]() $e$
. For a symmetric reflection, the projection of penetration will add to the pulse envelope[
Reference Hrdý71] as follows:
$e$
. For a symmetric reflection, the projection of penetration will add to the pulse envelope[
Reference Hrdý71] as follows:
This effect increases obviously with the Bragg angle and the number of consecutive reflections, and depends as well on the photon energy and material. The latter dependency is not straightforward. Higher photon energy usually leads to deeper penetration, but higher
![]() $Z$
of the material leads to stronger diffraction per lattice plane and hence reduced penetration.
$Z$
of the material leads to stronger diffraction per lattice plane and hence reduced penetration.
2.3 Interim summary
In this section, we elaborated on the factors influencing the polarization purity of X-rays in X-ray polarimetry. For high polarization purity of X-rays, the requirements on the polarizer are four-fold: channel-cut crystal, being made of high-quality material, multiple Bragg reflections
![]() $m=4$
,
$m=4$
,
![]() $m=6$
or more and avoiding detour reflections by azimuth angle tuning and material with low
$m=6$
or more and avoiding detour reflections by azimuth angle tuning and material with low
![]() $Z$
.
$Z$
.
For applications, not only purity
![]() $\mathcal{P}$
but also the integrated transmission
$\mathcal{P}$
but also the integrated transmission
![]() $T$
may play a role. This can fall back to the choice of
$T$
may play a role. This can fall back to the choice of
![]() $m$
, to considering an appropriate asymmetry angle
$m$
, to considering an appropriate asymmetry angle
![]() ${\alpha}_{\mathrm{c}}$
of the channel cut or even to a different material due to the
${\alpha}_{\mathrm{c}}$
of the channel cut or even to a different material due to the
![]() $Z$
dependence.
$Z$
dependence.
In 2022, Schulze et al.[
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59] reported an unprecedented purity of linear polarization of X-rays at the High Energy Density (HED) instrument of the European XFEL of
![]() ${\mathcal{P}=8\times {10}^{-11}}$
, provided by silicon channel cuts. They calculated the theoretical limitation of polarization purity as
${\mathcal{P}=8\times {10}^{-11}}$
, provided by silicon channel cuts. They calculated the theoretical limitation of polarization purity as
![]() $7\times {10}^{-14}$
by Equation (7) with the horizontal divergence of 0.27 μrad and a negligible vertical divergence. This emphasizes the importance of XFELs for further polarizer developments, since only XFELs can provide these low divergence beams.
$7\times {10}^{-14}$
by Equation (7) with the horizontal divergence of 0.27 μrad and a negligible vertical divergence. This emphasizes the importance of XFELs for further polarizer developments, since only XFELs can provide these low divergence beams.
In contrast, the polarization purity could not be determined better due to limited photon flux and integration time, since the XFEL was operated in SASE mode with large spectral bandwidth, not matched with the polarizer acceptance. Thus, the polarization-independent transmission
![]() $T$
was low, leading to
$T$
was low, leading to
![]() $NT\mathcal{P}$
photons arriving per pulse at the detector being at the noise limit. Asymmetric channel cuts may help improve
$NT\mathcal{P}$
photons arriving per pulse at the detector being at the noise limit. Asymmetric channel cuts may help improve
![]() $T$
thanks to Equation (11) (cf. Figure 9). However, the gain in spectral/angular acceptance is not very high. For
$T$
thanks to Equation (11) (cf. Figure 9). However, the gain in spectral/angular acceptance is not very high. For
![]() ${\alpha}_{\mathrm{c}}=-43{}^{\circ}$
, that is, 2° incidence onto the surface, the acceptance has increased by a factor approximately 5 while the beam footprint has increased by a factor approximately 27, requiring much larger channel-cut crystals.
${\alpha}_{\mathrm{c}}=-43{}^{\circ}$
, that is, 2° incidence onto the surface, the acceptance has increased by a factor approximately 5 while the beam footprint has increased by a factor approximately 27, requiring much larger channel-cut crystals.
3 X-ray polarimetry and vacuum birefringence
Many studies and concepts have been published for strong-field QED in general[ Reference Fedotov, Ilderton, Karbstein, King, Seipt, Taya and Torgrimsson39, Reference Di Piazza, Müller, Hatsagortsyan and Keitel73] and polarization effects in particular. Borysov et al.[ Reference Borysov, Heinemann, Ilderton, King and Potylitsyn74] proposed an indirect way to measure vacuum birefringence via experiments based on the photon-polarized nonlinear Breit–Wheeler (NBW) process. Xie et al. [ Reference Xie, Li and Tang75] reviewed the research progress of the pair production from vacuum in ultra-strong laser fields and investigated the effects of electric field polarizations on the number density of pair production. Koga et al. [ Reference Ko, Kang, Heo, Kim, Kim, Min, Yang, Baek, Choi, Mun, Park, Suh, Shin, Hu, Hong, Jung, Kim, Kim, Na, Park, Park, Jung, Jeong, Lee, Lee, Lee, Oh, Suh, Han, Kim, Jung, Kim, Lee, Lee, Sung, Mok, Yang, Parc, Lee, Lee, Shin, Kim, Kim, Lee, Park, Kim, Park, Eom, Rah, Kim, Nam, Park, Park, Kim, Kwon, An, Park, Kim, Hyun, Kim, Kim, Yu, Kim, Kang, Kim, Kim, Lee, Lee, Park, Koo, Kim and Lee76] presented the ultrahigh electric field generated by the interaction of micro-bubbles with ultra-intense laser pulses, which can be used to measure vacuum polarization via the bending of gamma rays traversing the imploded micro-bubble. Brezin and Itzykson[ Reference Brezin and Itzykson29] suggested using a laser beam and X-rays to study the small magnitude of effects predicted by QED. Correspondingly, X-ray polarimetry with excellent performance is proposed in detecting the vacuum birefringence phenomenon.
Currently, thanks to the development of ultra-intense optical lasers and XFELs, researchers[ Reference Ahmadiniaz, Cowan, Sauerbrey, Schramm, Schlenvoigt and Schützhold18– Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20, Reference Marklund and Lundin30, Reference Karbstein and Sundqvist33, Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35, Reference Karbstein36, Reference Xu, Shen, Xu and Liang77, Reference Koga, Murakami, Arefiev and Nakamiya78] proposed to probe the characteristics of the QED vacuum. Here, the highly purified linearly polarized XFEL interacts with an intense optical laser in vacuum. The XFEL will change its polarization state from linearly polarized to elliptically polarized. This state can be detected via ‘flipped photons’ behind a polarizer that is crossed to the original linear polarization and thereby proves the vacuum birefringence.
3.1 Vacuum birefringence in the universe
Before going into details for laboratory studies, intense astrophysical magnetic fields are ideal to explore vacuum birefringence by X-ray polarimetry. Taverna et al.[
Reference Taverna, Muleri, Turolla, Soffitta, Fabiani and Nobili79] calculated the polarization properties of X-ray radiation escaping from a magnetar magnetosphere via Monte Carlo code. By these simulations, they proved that polarimetric measurements are sufficiently sensitive to reveal QED effects due to vacuum polarization, and that X-ray polarimetry is an adequate tool to probe the ultra-strong magnetic fields in magnetars. In 2017, astronomers[
Reference Mignani, Testa, Caniulef, Taverna, Turolla, Zane and Wu80] experimentally proved the predictions of QED vacuum polarization effects via optical polarimetry measurement of isolated neutron stars. They measured the optical polarization degree to be
![]() $16.43\%\pm 5.26$
% and the polarization position angle to be
$16.43\%\pm 5.26$
% and the polarization position angle to be
![]() $145.39{}^{\circ}\pm 9.44{}^{\circ}$
, and claimed that was strong evidence for supporting the presence of the QED vacuum polarization effects, because those values are too high to be reproduced by models that neglect the QED vacuum polarization effects. However, Capparelli et al.[
Reference Capparelli, Damiano, Maiani and Polosa81] challenged this claim and compared the experimental data and theoretical calculations. They concluded that the polarization signal in Ref. [Reference Mignani, Testa, Caniulef, Taverna, Turolla, Zane and Wu80] was only a 3
$145.39{}^{\circ}\pm 9.44{}^{\circ}$
, and claimed that was strong evidence for supporting the presence of the QED vacuum polarization effects, because those values are too high to be reproduced by models that neglect the QED vacuum polarization effects. However, Capparelli et al.[
Reference Capparelli, Damiano, Maiani and Polosa81] challenged this claim and compared the experimental data and theoretical calculations. They concluded that the polarization signal in Ref. [Reference Mignani, Testa, Caniulef, Taverna, Turolla, Zane and Wu80] was only a 3
![]() $\sigma$
effect. They estimated the probability ratio of the polarization degree in both hypotheses with and without the birefringence effect, and concluded that a convincing proof of QED birefringence requires a degree of linear polarization exceeding 30%. In 2018, Caiazzo and Heyl[
Reference Caiazzo and Heyl82] found that X-rays from the accretion disks of black holes changed their polarization state as photons traveled through the magnetosphere, attributed to the vacuum becoming birefringent in the presence of a magnetic field. In 2020, Minami and Komatsu[
Reference Minami and Komatsu83] reported a new result of the cosmic birefringence angle
$\sigma$
effect. They estimated the probability ratio of the polarization degree in both hypotheses with and without the birefringence effect, and concluded that a convincing proof of QED birefringence requires a degree of linear polarization exceeding 30%. In 2018, Caiazzo and Heyl[
Reference Caiazzo and Heyl82] found that X-rays from the accretion disks of black holes changed their polarization state as photons traveled through the magnetosphere, attributed to the vacuum becoming birefringent in the presence of a magnetic field. In 2020, Minami and Komatsu[
Reference Minami and Komatsu83] reported a new result of the cosmic birefringence angle
![]() $\beta =\left(0.35^{\circ}\pm 14^{\circ}\right)$
$\beta =\left(0.35^{\circ}\pm 14^{\circ}\right)$
![]() $\left(68\%\ \mathrm{C.L.}\right)$
corresponding to the statistical significance of 2.4
$\left(68\%\ \mathrm{C.L.}\right)$
corresponding to the statistical significance of 2.4
![]() $\sigma$
, and reduced the systematic uncertainty by a factor of 2.
$\sigma$
, and reduced the systematic uncertainty by a factor of 2.
Although cosmic birefringence has been detected, its interpretation requires further models and assumptions but still can be controversial. This provides a solid case to study vacuum birefringence under controlled conditions in laboratories.

Figure 10 Proposed experimental setup for the demonstration of vacuum birefringence: a high-intensity laser pulse is focused by an F/2.5 off-axis parabolic mirror. A hole is drilled into the parabolic mirror in alignment with the z-axis (axes as indicated) in such a way that an X-ray pulse can propagate along the z-axis through the focal region of the high-intensity laser pulse. Using a polarizer–analyzer pair, the ellipticity of the X-ray pulse may be detected. Shown in grey: extension of the setup for the generation of counter-propagating laser pulses and a high-intensity standing wave, which may be used for pair creation. Reprinted from Ref. [Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20], with the permission of Elsevier.

Figure 11 Schematic views of the experimental setup. Top: several meter-long parts of the X-ray beamline centered around the interaction point with the optical components inside a vacuum chamber. Left: zoom into a cm-sized neighborhood of the focus where the cleaning electrodes will be placed. Bottom left: another zoom into the cleaned region. The focus of the cleaning laser is about 10 μm wide. However, only a fraction (pink) of the cleaned region will be employed as the interaction region, where the PW optical laser (
![]() $\sim 2\;\unicode{x3bc} \mathrm{m}$
) and the XFEL beam (
$\sim 2\;\unicode{x3bc} \mathrm{m}$
) and the XFEL beam (
![]() $\sim 0.5\;\unicode{x3bc} \mathrm{m}$
) are focused and superimposed. Bottom right: fundamental idea of probing QED vacuum birefringence caused by an intense optical laser with the XFEL beam. Beams are counter-propagating with their foci overlapping in space and time. To maximize the effect, the polarization directions must differ by 45°. A slight ellipticity in the polarization of the out-going probe pulse will occur. Used with the permission of IOP Publishing, from Ref. [Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]; permission conveyed through Copyright Clearance Center, Inc.
$\sim 0.5\;\unicode{x3bc} \mathrm{m}$
) are focused and superimposed. Bottom right: fundamental idea of probing QED vacuum birefringence caused by an intense optical laser with the XFEL beam. Beams are counter-propagating with their foci overlapping in space and time. To maximize the effect, the polarization directions must differ by 45°. A slight ellipticity in the polarization of the out-going probe pulse will occur. Used with the permission of IOP Publishing, from Ref. [Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]; permission conveyed through Copyright Clearance Center, Inc.
3.2 Concepts for vacuum birefringence laboratory studies
Studies that were conducted with static magnetic fields and optical lasers have already been introduced in Section 1. Those studies could not identify vacuum birefringence due to insufficient sensitivity. As astrophysical phenomena indicate vacuum birefringence but cannot be controlled, numerous conceptions and schemes of vacuum birefringence detection have been published. Some of them, based on X-ray polarimetry, are presented in the following.
3.2.1 PW lasers and XFELs
In 2006, Heinzl et al.[
Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20] considered a petawatt laser system with 140 fs pulse duration, 150 J pulse energy and
![]() ${10}^{22}\;\mathrm{W}/{\mathrm{cm}}^2$
intensity in the focal region to induce vacuum birefringence. A schematic diagram of the experimental setup is depicted in Figure 10. The high-power optical laser pulse is focused by an off-axis parabolic mirror (OAP), and the linearly polarized X-ray laser pulse collides with the optical laser pulse at the interaction area. Then, a small ellipticity of the X-ray pulse caused by vacuum birefringence will be detected. The whole process happens in a vacuum chamber.
${10}^{22}\;\mathrm{W}/{\mathrm{cm}}^2$
intensity in the focal region to induce vacuum birefringence. A schematic diagram of the experimental setup is depicted in Figure 10. The high-power optical laser pulse is focused by an off-axis parabolic mirror (OAP), and the linearly polarized X-ray laser pulse collides with the optical laser pulse at the interaction area. Then, a small ellipticity of the X-ray pulse caused by vacuum birefringence will be detected. The whole process happens in a vacuum chamber.
Schlenvoigt et al.[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19] proposed an experimental scheme (Figure 11) based on the European XFEL and HED instrument in conjunction with the Relativistic Laser at Xfel (ReLaX) laser system being developed by the Helmholtz International Beamline for Extreme Fields (HIBEF). In this figure, the main part is the setup for vacuum birefringence detection. The PW laser is also focused by an OAP into the interaction area. The propagation of the XFEL is worth introducing in detail. A well-collimated XFEL is measured by an intensity monitor (IM) to record the number of X-ray photons. Then, the XFEL becomes a linearly polarized beam with
![]() $\mathcal{P}\sim {10}^{-11}$
polarization purity after the polarizer (Pol). The first compound refractive lenses (CRLs) are used to focus the XFEL to the interaction point to overlap with the PW laser focus. The second CRLs are for re-collimation of the X-rays. The analyzer (Ana) is the same as the Pol in material and geometry but crossed to the Pol and only allows photons of flipped polarization to pass, which will be detected by the detector (Det). Comparing the photon numbers of the initial XFEL pulse and the polarization-flipped pulse, vacuum birefringence can be detected.
$\mathcal{P}\sim {10}^{-11}$
polarization purity after the polarizer (Pol). The first compound refractive lenses (CRLs) are used to focus the XFEL to the interaction point to overlap with the PW laser focus. The second CRLs are for re-collimation of the X-rays. The analyzer (Ana) is the same as the Pol in material and geometry but crossed to the Pol and only allows photons of flipped polarization to pass, which will be detected by the detector (Det). Comparing the photon numbers of the initial XFEL pulse and the polarization-flipped pulse, vacuum birefringence can be detected.
Moreover, the authors have studied the effect of plasma from residual gas particles on the signal of vacuum birefringence and proposed the method of vacuum cleaning. They plan to introduce another laser called a cleaning laser to ionize the gas particles, shown in yellow and named the cleaned volume, illustrated in the circle at the bottom left of Figure 11. The cleaned volume is much larger than the interaction volume, shown in pink. A static electric field is applied to remove charged particles from the cleaned volume. At the same time, the surrounding gas will repopulate the volume by diffusion, which can be mitigated by correct timing of the cleaning laser pulse. The bottom right shows the fundamental idea of probing QED vacuum birefringence by combining an XFEL and PW laser.
Subsequently, Shen et al.[
Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35] and Xu et al. [
Reference Xu, Shen, Xu and Liang77] presented an experimental design revolving around a 100 PW laser and a 12.914 keV XFEL beam with the Station of Extreme Light (SEL) at the Shanghai HIgh repetition rate XFEL aNd Extreme light (SHINE) facility. According to the parameters of the 100 PW laser and adopting the analysis of Schlenvoigt et al.[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19], the ellipticity is about
![]() $2\times {10}^{-10}$
and about 170 photons with flipped polarization should be produced by vacuum birefringence if the total photon number at the interaction is
$2\times {10}^{-10}$
and about 170 photons with flipped polarization should be produced by vacuum birefringence if the total photon number at the interaction is
![]() ${10}^{12}$
.
${10}^{12}$
.
There are further works presenting estimates for laser–XFEL studies, concentrating more on modeling and refined beam geometries[
Reference Karbstein and Sundqvist33,
Reference Karbstein, Gies, Reuter and Zepf84]. They also consider 30 J, 30 fs, 1 PW laser systems in conjunction with
![]() ${10}^{12}$
probe photons. Recently, Mosman and Karbstein[
Reference Mosman and Karbstein85] discussed in detail that modeling for ReLaX and the European XFEL as Schlenvoigt et al.[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19] did. However, they used more realistic laser and XFEL parameters, for example, the accelerator setpoint and bunch charge dependency on the number of probe photons, yielding
${10}^{12}$
probe photons. Recently, Mosman and Karbstein[
Reference Mosman and Karbstein85] discussed in detail that modeling for ReLaX and the European XFEL as Schlenvoigt et al.[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19] did. However, they used more realistic laser and XFEL parameters, for example, the accelerator setpoint and bunch charge dependency on the number of probe photons, yielding
![]() $N\sim {10}^{11}$
. This number is valid for the SASE mode of the European XFEL; the spectral matching aspect was published later[
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59], which effectively reduces the available number of photons. They also discussed XFEL pulse lengthening for channel-cut polarizers (cf. Section 2.2.4). Effectively, the polarizer before the interaction will stretch the X-ray pulses to approximately 100 fs. This can help in experiments to reduce the temporal jitter effect.
$N\sim {10}^{11}$
. This number is valid for the SASE mode of the European XFEL; the spectral matching aspect was published later[
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59], which effectively reduces the available number of photons. They also discussed XFEL pulse lengthening for channel-cut polarizers (cf. Section 2.2.4). Effectively, the polarizer before the interaction will stretch the X-ray pulses to approximately 100 fs. This can help in experiments to reduce the temporal jitter effect.
3.2.2 XFEL only
The common method of detecting vacuum birefringence is combining the XFEL with a PW-class optical laser. A novel way to detect vacuum birefringence by the collision of two consecutive XFEL pulses under a finite angle has been put forward by Karbstein et al.[
Reference Karbstein, Sundqvist, Schulze, Uschmann, Gies and Paulus86]. This idea takes the scaling of background field intensity (cf. Section 3.3) with wavelength,
![]() ${I}_{\mathrm{BG}}\propto {\lambda}^{-2}$
, into account and complements it with the higher repetition rate of XFELs compared to PW-class optical lasers.
${I}_{\mathrm{BG}}\propto {\lambda}^{-2}$
, into account and complements it with the higher repetition rate of XFELs compared to PW-class optical lasers.
Recently, the pulse duration of an XFEL was measured directly[
Reference Osaka, Inoue, Yamada, Inubushi, Matsumura, Sano, Tono, Yamauchi, Tamasaku and Yabashi87] to approximately 10 fs. This experiment demonstrates that the nonlinear regime of optics may be accessed in the X-ray domain, that is, sufficiently high photon densities can be produced. With a typical pulse energy of 1 mJ and the aforementioned pulse duration, the XFEL pulse power is about 100 GW. With
![]() $\lambda \sim 0.1\;\mathrm{nm}$
and further typical beam and focusing parameters (
$\lambda \sim 0.1\;\mathrm{nm}$
and further typical beam and focusing parameters (
![]() ${F}_{\#}\sim 100$
), spot sizes below 100 nm are reasonable[
Reference Schropp, Boye, Feldkamp, Hoppe, Patommel, Samberg, Stephan, Giewekemeyer, Wilke, Salditt, Gulden, Mancuso, Vartanyants, Weckert, Schöder, Burghammer and Schroer88,
Reference Schropp, Hoppe, Meier, Patommel, Seiboth, Lee, Nagler, Galtier, Arnold, Zastrau, Hastings, Nilsson, Uhlén, Vogt, Hertz and Schroer89], and thus focus areas of approximately
${F}_{\#}\sim 100$
), spot sizes below 100 nm are reasonable[
Reference Schropp, Boye, Feldkamp, Hoppe, Patommel, Samberg, Stephan, Giewekemeyer, Wilke, Salditt, Gulden, Mancuso, Vartanyants, Weckert, Schöder, Burghammer and Schroer88,
Reference Schropp, Hoppe, Meier, Patommel, Seiboth, Lee, Nagler, Galtier, Arnold, Zastrau, Hastings, Nilsson, Uhlén, Vogt, Hertz and Schroer89], and thus focus areas of approximately
![]() ${10}^{-10}\ {\mathrm{cm}}^2$
. As a result, intensities of
${10}^{-10}\ {\mathrm{cm}}^2$
. As a result, intensities of
![]() ${I}_{\mathrm{BG}}\sim {10}^{20}\ \mathrm{W}/{\mathrm{cm}}^2$
can be obtained with XFEL pulses for the background field. That is approximately 10% of optical laser peak intensities. While the ellipticity – being the photon polarization flip probability – scales as
${I}_{\mathrm{BG}}\sim {10}^{20}\ \mathrm{W}/{\mathrm{cm}}^2$
can be obtained with XFEL pulses for the background field. That is approximately 10% of optical laser peak intensities. While the ellipticity – being the photon polarization flip probability – scales as
![]() ${\delta}^2\propto {\left({I}_{\mathrm{BG}}\right)}^2$
, the number of flipped photons per unit time (e.g., operating hour) scales with the repetition rate, being easily
${\delta}^2\propto {\left({I}_{\mathrm{BG}}\right)}^2$
, the number of flipped photons per unit time (e.g., operating hour) scales with the repetition rate, being easily
![]() ${10}^2\ \mathrm{to}\ {10}^4$
Hz and 1 MHz in future facilities (cf. Table 3). As a consequence, the number of flipped photons per unit time can compete with or even exceed the numbers of XFEL–laser combined schemes. Technically, a PW-class laser installation alongside an XFEL is not necessary, but an even more complex X-ray beam path must be realized.
${10}^2\ \mathrm{to}\ {10}^4$
Hz and 1 MHz in future facilities (cf. Table 3). As a consequence, the number of flipped photons per unit time can compete with or even exceed the numbers of XFEL–laser combined schemes. Technically, a PW-class laser installation alongside an XFEL is not necessary, but an even more complex X-ray beam path must be realized.
Table 3 Overview of XFEL facilities. Bold facility names indicate facilities with an ultra-intense laser in operation. Italic represents planned facilities. Adapted from Ref. [Reference Nakamiya and Homma90], licensed under CC BY-NC-ND 4.0.

From the installation diagram (Figure 12) we can see that the XFEL beam is focused twice to the interaction region from different directions. This employs the pulse train, such that pulse
![]() $n$
is the probe for pulse
$n$
is the probe for pulse
![]() $n+1$
. Along with the beam path, the first set of CRLs generates the pump pulse (
$n+1$
. Along with the beam path, the first set of CRLs generates the pump pulse (
![]() $b=2$
), where no high polarization purity is required. Further downstream follows a CRL to re-collimate the beam for a delay path, matching the pulse repetition time. Then the XFEL passes through the polarizer made by a channel-cut diamond to become the probe pulse (
$b=2$
), where no high polarization purity is required. Further downstream follows a CRL to re-collimate the beam for a delay path, matching the pulse repetition time. Then the XFEL passes through the polarizer made by a channel-cut diamond to become the probe pulse (
![]() $b=1$
). Karbstein et al.[
Reference Karbstein, Sundqvist, Schulze, Uschmann, Gies and Paulus86] also mentioned the losses and the pulse deformations of the XFEL pulse caused by optical elements. In the meantime, each XFEL pulse train should be controlled well to achieve the best possible spatio-temporal overlap of the focused pump and probe beams. Furthermore, each optical element must be of sufficient perfection, for example, the high reflectivity of diamond crystals and the high perfect focus of CRLs.
$b=1$
). Karbstein et al.[
Reference Karbstein, Sundqvist, Schulze, Uschmann, Gies and Paulus86] also mentioned the losses and the pulse deformations of the XFEL pulse caused by optical elements. In the meantime, each XFEL pulse train should be controlled well to achieve the best possible spatio-temporal overlap of the focused pump and probe beams. Furthermore, each optical element must be of sufficient perfection, for example, the high reflectivity of diamond crystals and the high perfect focus of CRLs.

Figure 12 Illustration of the experimental setup utilizing compound refractive lenses (CRLs) to focus and re-collimate the XFEL beam. Reflections at diamond crystals change the propagation direction, and a pair of diamond quasi-channel-cuts serve as the polarizer and analyzer, respectively. The original XFEL beam is focused with a CRL to constitute the pump field; the beam focus defines the interaction point. Subsequently, it is defocused with a CRL and by reflection at two diamond crystals directed back to the interaction point under an angle of
![]() $ \vartheta_{\mathrm{coll}}$
. Before reaching the interaction point, it is polarized with a diamond polarizer and the resulting probe beam focused to the interaction point with a CRL. Finally, it is defocused with another CRL, analyzed with a diamond analyzer and the signal registered with a charge-coupled device. Taken from Ref. [Reference Karbstein, Sundqvist, Schulze, Uschmann, Gies and Paulus86], licensed under CC BY 4.0.
$ \vartheta_{\mathrm{coll}}$
. Before reaching the interaction point, it is polarized with a diamond polarizer and the resulting probe beam focused to the interaction point with a CRL. Finally, it is defocused with another CRL, analyzed with a diamond analyzer and the signal registered with a charge-coupled device. Taken from Ref. [Reference Karbstein, Sundqvist, Schulze, Uschmann, Gies and Paulus86], licensed under CC BY 4.0.
Apart from X-ray polarimetry, scientists have presented a different approach for measuring vacuum birefringence using multi-MeV to GeV photons[
Reference King and Elkina37,
Reference Nakamiya and Homma91]. King and Elkina[
Reference King and Elkina37] carried out the analytical calculations and numerical simulations for the measurement of vacuum birefringence by multi-MeV photons, instead of X-ray or optical photons. Nakamiya and Homma[
Reference Nakamiya and Homma91] proposed combining a 10 PW laser system with a 1 GeV gamma-ray photon source to probe the vacuum birefringence effect and designed the gamma-ray polarimeter to measure the polarization flip of the probe gamma-rays. They derived theoretically the phase retardation of GeV probe photons via pairwise topology of the Bethe–Heitler process in a polarimeter, and concluded it would be possible to observe the vacuum birefringence effect with the accuracy of 4.7% for the averaged phase retardation
![]() $\left\langle G\right\rangle$
of 0.72 if
$\left\langle G\right\rangle$
of 0.72 if
![]() ${10}^4$
conversion pairs are available.
${10}^4$
conversion pairs are available.
3.3 Estimated ellipticity
Referring to the previous contents, the highly linearly polarized XFEL changes its polarization state to elliptically polarized when it propagates through a vacuum that is polarized by focusing a light beam as the background field. This is slightly different from the quasi-constant fields employed in studies with optical laser polarimetry (cf. Section 1). The calculations lead to similar expressions, such that a difference of the refractive index, Equation (4), leads to a phase shift of two circular polarization components of the linearly polarized XFEL, as follows:
where
![]() $\alpha$
is again the fine structure constant,
$\alpha$
is again the fine structure constant,
![]() ${I}_{\mathrm{crit}}\approx 4.4\times {10}^{29}\;\mathrm{W}/{\mathrm{cm}}^2$
is the critical intensity derived from Equation (3),
${I}_{\mathrm{crit}}\approx 4.4\times {10}^{29}\;\mathrm{W}/{\mathrm{cm}}^2$
is the critical intensity derived from Equation (3),
![]() $\lambda$
is the wavelength of the radiation experiencing the vacuum birefringence (here XFEL),
$\lambda$
is the wavelength of the radiation experiencing the vacuum birefringence (here XFEL),
![]() ${I}_{\mathrm{BG}}$
is the intensity of the background field and
${I}_{\mathrm{BG}}$
is the intensity of the background field and
![]() $\mathrm{\ell}$
is the interaction length. The ellipticity of the XFEL, probing the vacuum birefringence, is as follows:
$\mathrm{\ell}$
is the interaction length. The ellipticity of the XFEL, probing the vacuum birefringence, is as follows:
It must be noted that this effect is maximized if (i) the background field is counter-propagating to the probing pulse and (i) the background field polarization is 45° to the probe field polarization[ Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20, Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35].
Heinzl et al.[
Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20] considered for a Gaussian optical laser beam as the background field to set
![]() $\mathrm{\ell}={z}_{\mathrm{Rayleigh},\mathrm{BG}}$
. That would be correct if the background field had no time dependence during the interaction. However, they consider the case of a pulsed laser, either in a counter-propagating way or as a standing wave (grey part in Figure 10). This leads in both variants to a time dependence, such that the time dependence of the probe must be considered.
$\mathrm{\ell}={z}_{\mathrm{Rayleigh},\mathrm{BG}}$
. That would be correct if the background field had no time dependence during the interaction. However, they consider the case of a pulsed laser, either in a counter-propagating way or as a standing wave (grey part in Figure 10). This leads in both variants to a time dependence, such that the time dependence of the probe must be considered.
Schlenvoigt et al.[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19] refined the analytical framework of Heinzl et al. [
Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20] by taking their result as a differential phase shift and integrated analytically for counter-propagating Gaussian beams with Gaussian pulse shapes, and accounted for temporal and spatial offsets, enabling an analysis for jittering conditions. This approach showed that
![]() $\mathrm{\ell}$
can be determined by the geometric pulse length
$\mathrm{\ell}$
can be determined by the geometric pulse length
![]() $c\cdot {\tau}_{\mathrm{BG}}$
, but does not yield analytical expressions. In comparison to Heinzl et al., assuming here two times higher laser intensity, Schlenvoigt et al. estimated a factor of 10 less ellipticity due to their more accurate modeling. Mosman and Karbstein[
Reference Mosman and Karbstein85] referred to the same facility but with again reduced laser pulse energy and thus reduced peak intensity (1/3 that of Schlenvoigt et al.) and found a reasonably well down-scaled ellipticity of
$c\cdot {\tau}_{\mathrm{BG}}$
, but does not yield analytical expressions. In comparison to Heinzl et al., assuming here two times higher laser intensity, Schlenvoigt et al. estimated a factor of 10 less ellipticity due to their more accurate modeling. Mosman and Karbstein[
Reference Mosman and Karbstein85] referred to the same facility but with again reduced laser pulse energy and thus reduced peak intensity (1/3 that of Schlenvoigt et al.) and found a reasonably well down-scaled ellipticity of
![]() $3.5\times {10}^{-13}$
.
$3.5\times {10}^{-13}$
.
In view of considerably differing estimates due to many influencing factors, we only provide scalings[ Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19, Reference Mosman and Karbstein85] with the relevant quantities. First, we address the background field intensity:
where
![]() ${P}_{\mathrm{BG}}$
,
${P}_{\mathrm{BG}}$
,
![]() ${E}_{\mathrm{BG}}$
and
${E}_{\mathrm{BG}}$
and
![]() ${\tau}_{\mathrm{BG}}$
denote the pulse power, pulse energy and pulse duration, respectively, and
${\tau}_{\mathrm{BG}}$
denote the pulse power, pulse energy and pulse duration, respectively, and
![]() ${\lambda}_{\mathrm{BG}}$
,
${\lambda}_{\mathrm{BG}}$
,
![]() ${w}_{\mathrm{BG}}$
and
${w}_{\mathrm{BG}}$
and
![]() ${F}_{\#}$
denote the wavelength, focus waist and focusing F-number (ratio of focal length to effective beam diameter), respectively. In the next step, the ellipticity scales as follows:
${F}_{\#}$
denote the wavelength, focus waist and focusing F-number (ratio of focal length to effective beam diameter), respectively. In the next step, the ellipticity scales as follows:
with
![]() $\lambda$
again the wavelength of the probing X-ray beam, not the driving optical laser. This again shows the importance of short probe wavelengths and high intensities. However, it must be kept in mind that there can be couplings to
$\lambda$
again the wavelength of the probing X-ray beam, not the driving optical laser. This again shows the importance of short probe wavelengths and high intensities. However, it must be kept in mind that there can be couplings to
![]() $\mathrm{\ell}$
or other parameters, depending on the scheme. For example, a shorter background pulse duration increases the intensity but reduces the interaction length
$\mathrm{\ell}$
or other parameters, depending on the scheme. For example, a shorter background pulse duration increases the intensity but reduces the interaction length
![]() $\mathrm{\ell}$
, such that the effect can be quite weak.
$\mathrm{\ell}$
, such that the effect can be quite weak.
The previous equations can be combined and yield, employing for clarity
![]() $\mathrm{\hslash}{\omega}_{\mathrm{probe}}$
instead of
$\mathrm{\hslash}{\omega}_{\mathrm{probe}}$
instead of
![]() $\lambda$
, the following:
$\lambda$
, the following:
 $$\begin{align}{\delta}^2\propto \frac{E_{\mathrm{BG}}^2{\left(\mathrm{\hslash}{\omega}_{\mathrm{probe}}\right)}^2}{\tau_{\mathrm{BG}}^2{\lambda}_{\mathrm{BG}}^4{F}_{\#}^4}.\end{align}$$
$$\begin{align}{\delta}^2\propto \frac{E_{\mathrm{BG}}^2{\left(\mathrm{\hslash}{\omega}_{\mathrm{probe}}\right)}^2}{\tau_{\mathrm{BG}}^2{\lambda}_{\mathrm{BG}}^4{F}_{\#}^4}.\end{align}$$
Table 4 summarizes the ellipticity values for the different XFEL-PW proposals discussed in Section 3.2.1. Please note that Heinzl et al.[ Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20] did employ a rough estimate for beam shapes and interaction length, leading to relatively large estimated ellipticity for a 1 PW laser.
Table 4 Comparison of laser parameters and expected ellipticity (for 13 keV photon energy) of the proposed experiments. Note that Heinzl et al.[ Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf20] did not compute the effects of pulse duration and beam shapes, leading to a relatively large ellipticity.

3.4 Readiness review
Regarding the detection of such ellipticity, a polarimeter with crossed polarizations would be realized. The ellipticity is effectively the probability that a probe beam photon flips its polarization state. Therefore, referring back to Section 2.1 and considering
![]() $N$
photons being emitted at the source and passing through an arrangement with polarization-independent transmission
$N$
photons being emitted at the source and passing through an arrangement with polarization-independent transmission
![]() $T$
, approximately
$T$
, approximately
![]() $NT{\delta}^2$
flipped photons would arrive at a detector, whereas approximately
$NT{\delta}^2$
flipped photons would arrive at a detector, whereas approximately
![]() $NT\mathcal{P}$
photons would be not flipped but still transmitted towards the detector, being a background[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]. Thus there are three challenges for detection:
$NT\mathcal{P}$
photons would be not flipped but still transmitted towards the detector, being a background[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]. Thus there are three challenges for detection:
-
(i) the large number of photons per pulse
 $N$
;
$N$
; -
(ii) the high overall transmission
 $T$
;
$T$
; -
(iii) the ellipticity
 ${\delta}^2$
being competitive with or exceeding purity
${\delta}^2$
being competitive with or exceeding purity
 $\mathcal{P}$
.
$\mathcal{P}$
.
In addition, such detection would require the integration of photons to achieve a certain confidence limit, probably by a number of repetitions
![]() $m$
. The following was shown[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]:
$m$
. The following was shown[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]:
The integration time can be reduced by
![]() $N$
,
$N$
,
![]() $T$
and
$T$
and
![]() ${\delta}^2/\mathcal{P}$
equally. In the following we will address these points.
${\delta}^2/\mathcal{P}$
equally. In the following we will address these points.
3.4.1 XFEL facilities
XFELs are indispensable sources for structural analysis and have contributed to the development of ultra-fast processes. XFEL facilities have blossomed all over the world[ Reference Huang, Deng, Liu, Wang and Zhao90]. In Europe, Deutsches Elektronen-Synchrotron (DESY)[ Reference Ackermann, Asova, Ayvazyan, Azima, Baboi, Bähr, Balandin, Beutner, Brandt, Bolzmann, Brinkmann, Brovko, Castellano, Castro, Catani, Chiadroni, Choroba, Cianchi, Costello, Cubaynes, Dardis, Decking, Delsim-Hashemi, Delserieys, Di Pirro, Dohlus, Düsterer, Eckhardt, Edwards, Faatz, Feldhaus, Flöttmann, Frisch, Fröhlich, Garvey, Gensch, Gerth, Görler, Golubeva, Grabosch, Grecki, Grimm, Hacker, Hahn, Han, Honkavaara, Hott, Hüning, Ivanisenko, Jaeschke, Jalmuzna, Jezynski, Kammering, Katalev, Kavanagh, Kennedy, Khodyachykh, Klose, Kocharyan, Körfer, Kollewe, Koprek, Korepanov, Kostin, Krassilnikov, Kube, Kuhlmann, Lewis, Lilje, Limberg, Lipka, Löhl, Luna, Luong, Martins, Meyer, Michelato, Miltchev, Möller, Monaco, Müller, Napieralski, Napoly, Nicolosi, Nölle, Nuñez, Oppelt, Pagani, Paparella, Pchalek, Pedregosa-Gutierrez, Petersen, Petrosyan, Petrosyan, Petrosyan, Pflüger, Plönjes, Poletto, Pozniak, Prat, Proch, Pucyk, Radcliffe, Redlin, Rehlich, Richter, Roehrs, Roensch, Romaniuk, Ross, Rossbach, Rybnikov, Sachwitz, Saldin, Sandner, Schlarb, Schmidt, Schmitz, Schmüser, Schneider, Schneidmiller, Schnepp, Schreiber, Seidel, Sertore, Shabunov, Simon, Simrock, Sombrowski, Sorokin, Spanknebel, Spesyvtsev, Staykov, Steffen, Stephan, Stulle, Thom, Tiedtke, Tischer, Toleikis, Treusch, Trines, Tsakov, Vogel, Weiland, Weise, Wellhöfer, Wendt, Will, Winter, Wittenburg, Wurth, Yeates, Yurkov, Zagorodnov and Zapfe92, 93], one of the accelerator centers, contains three large accelerators: PETRA III, FLASH and European XFEL. FLASH supplies soft X-rays and PETRA III and EuXFEL supply hard X-rays. Italian Elettra Sincrotrone Trieste[ 94] has two advanced light sources: Elettra and FERMI. The third-generation synchrotron radiation facility Elettra produces synchrotron radiation in a wavelength range from infrared to hard X-rays, while FERMI is a seeded free electron laser working in the ultraviolet and soft X-ray range. SwissFEL[ Reference Milne, Schietinger, Aiba, Alarcon, Alex, Anghel, Arsov, Beard, Beaud, Bettoni, Bopp, Brands, Brönnimann, Brunnenkant, Calvi, Citterio, Craievich, Divall, Dällenbach, D’Amico, Dax, Deng, Dietrich, Dinapoli, Divall, Dordevic, Ebner, Erny, Fitze, Flechsig, Follath, Frei, Gärtner, Ganter, Garvey, Geng, Gorgisyan, Gough, Hauff, Hauri, Hiller, Humar, Hunziker, Ingold, Ischebeck, Janousch, Juranić, Jurcevic, Kaiser, Kalantari, Kalt, Keil, Kittel, Knopp, Koprek, Lemke, Lippuner, Sancho, Löhl, Lopez-Cuenca, Märki, Marcellini, Marinkovic, Martiel, Menzel, Mozzanica, Nass, Orlandi, Loch, Panepucci, Paraliev, Patterson, Pedrini, Pedrozzi, Pollet, Pradervand, Prat, Radi, Raguin, Redford, Rehanek, Réhault, Reiche, Ringele, Rittmann, Rivkin, Romann, Ruat, Ruder, Sala, Schebacher, Schilcher, Schlott, Schmidt, Schmitt, Shi, Stadler, Stingelin, Sturzenegger, Szlachetko, Thattil, Treyer, Trisorio, Tron, Vetter, Vicario, Voulot, Wang, Zamofing, Zellweger, Zennaro, Zimoch, Abela, Patthey and Braun95, 96] is Switzerland’s X-ray free electron laser with a hard X-ray free electron laser with 0.1 nm wavelength and 20 fs pulse duration at the Paul Scherrer Institute (PSI).
In the USA, the Linac Coherent Light Source (LCLS)[ Reference Emma, Akre, Arthur, Bionta, Bostedt, Bozek, Brachmann, Bucksbaum, Coffee, Decker, Ding, Dowell, Edstrom, Fisher, Frisch, Gilevich, Hastings, Hays, Ph, Huang, Iverson, Loos, Messerschmidt, Miahnahri, Moeller, Nuhn, Pile, Ratner, Rzepiela, Schultz, Smith, Stefan, Tompkins, Turner, Welch, White, Wu, Yocky and Galayda97, 98] at SLAC achieved the first lasing and FEL saturation at 0.15 nm in 2009. Its upgrade LCLS-II[ Reference Galayda99] is designed to produce high-energy X-rays covering the energy range from 200 eV to 1.5 keV for soft X-rays and from 1 to 5 keV for hard X-rays. A further upgrade[ Reference Raubenheimer100] from 4 to 8 GeV beam energy will extend the photon energy range to at least 12.8 keV.
In Asia, the first FEL facility was the SPring-8 Ångström Compact Free-Electron Laser (SACLA)[ Reference Pile101] in Japan, with a peak X-ray laser power of 1 GW and wavelength of 0.1 nm. It has matured to multi-beamline, soft and hard X-ray operation[ Reference Yabashi, Tanaka and Ishikawa102, Reference Tono, Hara, Yabashi and Tanaka103] and extreme intensities[ Reference Osaka, Inoue, Yamada, Inubushi, Matsumura, Sano, Tono, Yamauchi, Tamasaku and Yabashi87]. The Pohang Accelerator Laboratory X-ray Free Electron Laser (PAL-XFEL)[ Reference Ko, Kang, Heo, Kim, Kim, Min, Yang, Baek, Choi, Mun, Park, Suh, Shin, Hu, Hong, Jung, Kim, Kim, Na, Park, Park, Jung, Jeong, Lee, Lee, Lee, Oh, Suh, Han, Kim, Jung, Kim, Lee, Lee, Sung, Mok, Yang, Parc, Lee, Lee, Shin, Kim, Kim, Lee, Park, Kim, Park, Eom, Rah, Kim, Nam, Park, Park, Kim, Kwon, An, Park, Kim, Hyun, Kim, Kim, Yu, Kim, Kang, Kim, Kim, Lee, Lee, Park, Koo, Kim and Lee76] produces wavelengths of 0.1 and 1 nm for hard and soft X-rays, respectively. In China there are two facilities[ Reference Liu, Feng, Gu, Gao, Deng, Zhang, Sun, Chen, Zhang, Fang, Wang, Zhou, Leng, Gu, Yin, Gu, Fang, Wang and Zhao104, Reference Shen, Ji, Zhang, Bu and Xu105]: the Soft X-ray Free Electron Laser (SXFEL) performs the shortest wavelength of 2 nm, and the hard XFEL SHINE with a 0.05 nm wavelength is being constructed. All of these facilities with brilliant X-rays enable scientists to gain insights into the properties, ultrafast processes and essences of matter.
We are not discussing synchrotron sources for two reasons. They are currently limited in beam divergence and thus in polarization purity. Furthermore, their pulses are much longer than background field pulses and contain far fewer photons than XFEL pulses.
In the context of X-ray polarimetry of vacuum birefringence, it must be noted that probe beam photon numbers are often over-estimated in experiment proposals. Typical XFEL pulse energies are of the order of 1 mJ, which yields at 12 keV about
![]() ${10}^{11}$
photons[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]. In addition, the usual spectral bandwidth of XFELs is of the order of 1% in SASE mode. With self-seeding schemes[
Reference Saldin, Schneidmiller, Shvyd’ko and Yurkov106–
Reference Amann, Berg, Blank, Decker, Ding, Emma, Feng, Frisch, Fritz, Hastings, Huang, Krzywinski, Lindberg, Loos, Lutman, Nuhn, Ratner, Rzepiela, Shu, Shvyd’ko, Spampinati, Stoupin, Terentyev, Trakhtenberg, Walz, Welch, Wu, Zholents and Zhu108], a reduction to 10–4 is possible at the cost of reduced pulse energy. This sets requirements on the spectral/angular acceptance of crystal optics, such as channel-cut crystal polarizers, particularly the widths of Bragg reflectivity curves, as shown in Figure 5.
${10}^{11}$
photons[
Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19]. In addition, the usual spectral bandwidth of XFELs is of the order of 1% in SASE mode. With self-seeding schemes[
Reference Saldin, Schneidmiller, Shvyd’ko and Yurkov106–
Reference Amann, Berg, Blank, Decker, Ding, Emma, Feng, Frisch, Fritz, Hastings, Huang, Krzywinski, Lindberg, Loos, Lutman, Nuhn, Ratner, Rzepiela, Shu, Shvyd’ko, Spampinati, Stoupin, Terentyev, Trakhtenberg, Walz, Welch, Wu, Zholents and Zhu108], a reduction to 10–4 is possible at the cost of reduced pulse energy. This sets requirements on the spectral/angular acceptance of crystal optics, such as channel-cut crystal polarizers, particularly the widths of Bragg reflectivity curves, as shown in Figure 5.
A relative spectral width of
![]() ${10}^{-4}$
at
${10}^{-4}$
at
![]() ${\theta}_{\mathrm{B}}=45{}^{\circ}$
, matching the self-seeding bandwidth, requires a reflectivity curve width of
${\theta}_{\mathrm{B}}=45{}^{\circ}$
, matching the self-seeding bandwidth, requires a reflectivity curve width of
![]() ${10}^{-4}\ \mathrm{rad}={20}^{"}$
. Thus, the dashed curve in Figure 5, having a width of approximately
${10}^{-4}\ \mathrm{rad}={20}^{"}$
. Thus, the dashed curve in Figure 5, having a width of approximately
![]() ${6}^{"}$
, would have a spectral transmission of approximately 0.3 for self-seeded FEL pulses. Using an asymmetric cut (see Section 2.2.2), can increase the reflectivity curve width. As an example, in order to widen the curve by the required factor of approximately 3, an asymmetry angle
${6}^{"}$
, would have a spectral transmission of approximately 0.3 for self-seeded FEL pulses. Using an asymmetric cut (see Section 2.2.2), can increase the reflectivity curve width. As an example, in order to widen the curve by the required factor of approximately 3, an asymmetry angle
![]() ${\alpha}_{\mathrm{c}}\sim -40{}^{\circ}$
would be necessary. This would increase the beam footprint on the channel-cut crystal surface by approximately 10.
${\alpha}_{\mathrm{c}}\sim -40{}^{\circ}$
would be necessary. This would increase the beam footprint on the channel-cut crystal surface by approximately 10.
For higher photon energies, for example, the solid curve in Figure 5 for
![]() ${E}_{\mathrm{ph}}\sim 10\;\mathrm{keV}$
, the reflectivity curves become narrower due to deeper penetration. As a consequence, improving the bandwidth by the asymmetry angle
${E}_{\mathrm{ph}}\sim 10\;\mathrm{keV}$
, the reflectivity curves become narrower due to deeper penetration. As a consequence, improving the bandwidth by the asymmetry angle
![]() ${\alpha}_{\mathrm{c}}$
becomes increasingly impractical.
${\alpha}_{\mathrm{c}}$
becomes increasingly impractical.
3.4.2 PW-class laser facilities
Ultra-intense pulsed lasers are known to produce the highest light intensities on Earth and are thus favorable tools to generate the background field in their focus, polarizing the vacuum helped by a counter-propagating probe light. Table 4 has already provided estimated ellipticities for relevant peak intensities. Those intensities are in reach of currently available laser technology. Recently, laser scientists at the Center for Relativistic Laser Science (CoReLS) in Korea reported a peak laser intensity exceeding
![]() ${10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
[
Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam109], generated from a 4 PW laser pulse.
${10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
[
Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam109], generated from a 4 PW laser pulse.
Ultra-intense laser systems are nowadays commercially available and are widely employed. They are in general based on the chirped pulse amplification scheme (CPA)[ Reference Strickland and Mourou110] and exhibit pulse durations of from approximately 10 fs to approximately 1 ps, and typical wavelengths are 800 nm or 1.05 μm. An overview can be found at The International Committee on Ultrahigh Intensity Lasers (ICUIL)[ 111], where they provide an interactive map[ 112].
PW-class lasers are currently the top class of existing facilities, but there are several dozen and hence too many to list them all. Here we concentrate on facilities and projects significantly exceeding 1 PW.
The Extreme Light Infrastructure (ELI)[ Reference Gales, Tanaka, Balabanski, Negoita, Stutman, Tesileanu, Ur, Ursescu, Andrei, Ataman, Cernaianu, D’Alessi, Dancus, Diaconescu, Djourelov, Filipescu, Ghenuche, Ghita, Matei, Seto, Zeng and Zamfir113– 116] is an advanced laser-based research infrastructure with multiple sites. One of the sites is Extreme Light Infrastructure Nuclear Physics (ELI-NP), which succeeded in delivering the 10 PW @ 1 shot per minute in 2019.
In the UK, the Central Laser Facility (CLF)[
Reference Chekhlov, Divall, Ertel, Hawkes, Hooker, Ross, Matousek, Hernandez-Gomez, Musgrave, Tang, Winstone, Neely, Clarke, Foster, Hancock, Wyborn and Collier117,
118], part of the Rutherford Appleton Laboratory, is dedicated to high-energy laser systems. There are five laser facilities: ULTRA, Artemis, OCTOPUS, Gemini and Vulcan. Here, Gemini is a dual beam laser system with 2 × 15 J, 30 fs laser pulses. Vulcan has two kinds of laser modes. In its long pulse mode, the laser energy is up to 2.6 kJ with nanosecond pulse duration. In the short pulse mode, it has up to 1 PW peak power with 500 fs pulse duration and the focal intensity is about
![]() ${10}^{21}\ \mathrm{W}/{\mathrm{cm}}^2$
. Soon, the peak power will be increased from 1 PW (500 J in 500 fs) to 20 PW (400 J in 20 fs). It will be a unique beamline to examine matter under extreme conditions.
${10}^{21}\ \mathrm{W}/{\mathrm{cm}}^2$
. Soon, the peak power will be increased from 1 PW (500 J in 500 fs) to 20 PW (400 J in 20 fs). It will be a unique beamline to examine matter under extreme conditions.
In France, the Apollon laser system is a multi-beam, multi-petawatt facility to generate 10 PW pulses of 150 J energy and 15 fs (full width at half maximum (FWHM)) duration at a repetition rate of 1 shot per minute. The first available laser beam delivered on-target pulses of 10 J average energy, 24 fs duration and 1 PW nominal power in 2021[ Reference Burdonov, Fazzini, Lelasseux, Albrecht, Antici, Ayoul, Beluze, Cavanna, Ceccotti, Chabanis, Chaleil, Chen, Chen, Consoli, Cuciuc, Davoine, Delaneau, d’Humières, Dubois, Evrard, Filippov, Freneaux, Forestier-Colleoni, Gremillet, Horny, Lancia, Lecherbourg, Lebas, Leblanc, Ma, Martin, Negoita, Paillard, Papadopoulos, Perez, Pikuz, Qi, Quéré, Ranc, Söderström, Scisciò, Sun, Vallières, Wang, Yao, Mathieu, Audebert and Fuchs119].
The Institute of Applied Physics of the Russian Academy of Sciences has established a large infrastructure project, the Exawatt Center for Extreme Light Studies (XCELS)[
Reference Mukhin, Soloviev, Perevezentsev, Shaykin, Ginzburg, Kuzmin, Mart’yanov, Shaikin, Kuzmin, Mironov, Yakovlev and Khazanov120–
122]. The aim of the project is to build high-power lasers with 200 PW power and 25 fs pulse duration by assembling 12 identical laser channels with 15 PW power for each. The intensity in the focus is expected to be approximately
![]() ${10}^{25}\ \mathrm{W}/{\mathrm{cm}}^2$
. This provides an opportunity to peer into the fundamental processes and unknown phenomena of high-energy physics.
${10}^{25}\ \mathrm{W}/{\mathrm{cm}}^2$
. This provides an opportunity to peer into the fundamental processes and unknown phenomena of high-energy physics.
Furthermore, the project of Shanghai HIgh repetition rate XFEL aNd Extreme light facility (SHINE) was founded[
Reference Gan, Yu, Wang, Liu, Xu, Li, Li, Yu, Wang, Liu, Chen, Peng, Xu, Yao, Zhang, Chen, Tang, Wang, Yin, Liang, Leng, Li and Xu123] in Shanghai, China. In the future, the SEL of SHINE will provide a laser system with 100 PW and an expected focused laser intensity of
![]() $2\times {10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
[
Reference Wang, Liu, Lu, Chen, Long, Li, Chen, Chen, Bai, Li, Peng, Liu, Wu, Wang, Li, Xu, Liang, Leng and Li124]. This is the basis for the proposed experiments[
Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35,
Reference Xu, Shen, Xu and Liang77] at SHINE.
$2\times {10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
[
Reference Wang, Liu, Lu, Chen, Long, Li, Chen, Chen, Bai, Li, Peng, Liu, Wu, Wang, Li, Xu, Liang, Leng and Li124]. This is the basis for the proposed experiments[
Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35,
Reference Xu, Shen, Xu and Liang77] at SHINE.
In view of vacuum birefringence, the gain of ellipticity
![]() ${\delta}^2$
with laser peak intensity is obviously quite strong,
${\delta}^2$
with laser peak intensity is obviously quite strong,
![]() ${\delta}^2\propto {\left({I}_{\mathrm{BG}}\right)}^2$
(see Equation (16a)). This is of particular importance for the trade-off of ellipticity against purity
${\delta}^2\propto {\left({I}_{\mathrm{BG}}\right)}^2$
(see Equation (16a)). This is of particular importance for the trade-off of ellipticity against purity
![]() $\mathcal{P}$
. Table 4 indicates that an intensity of
$\mathcal{P}$
. Table 4 indicates that an intensity of
![]() ${I}_{\mathrm{BG}}\sim 2\times {10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
can yield an ellipticity
${I}_{\mathrm{BG}}\sim 2\times {10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
can yield an ellipticity
![]() ${\delta}^2\sim 2\times {10}^{-10}$
, exceeding the best purities so far measured,
${\delta}^2\sim 2\times {10}^{-10}$
, exceeding the best purities so far measured,
![]() $\mathcal{P}\sim {10}^{-11}$
(cf. Table 5). In this way, the signal would always exceed the background from the finite extinction. In addition, it should be noted that such intensity has already been demonstrated with a 4 PW laser system[
Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam109].
$\mathcal{P}\sim {10}^{-11}$
(cf. Table 5). In this way, the signal would always exceed the background from the finite extinction. In addition, it should be noted that such intensity has already been demonstrated with a 4 PW laser system[
Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam109].
Table 5 Timeline of precision X-ray polarimetry. Here,
![]() $m$
denotes the number of reflections per channel-cut crystal,
$m$
denotes the number of reflections per channel-cut crystal,
![]() ${\sigma}_{\mathrm{H}}$
and
${\sigma}_{\mathrm{H}}$
and
![]() ${\sigma}_{\mathrm{V}}$
represent the beam divergence,
${\sigma}_{\mathrm{V}}$
represent the beam divergence,
![]() $\mathcal{P}$
is the obtained polarization purity and
$\mathcal{P}$
is the obtained polarization purity and
![]() ${\mathcal{P}}_{\mathrm{Divergence}}^{\mathrm{Limit}}$
is calculated from the divergence according to Equation (7). For the current record[
Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72], the nominal instrument’s beam divergence was reduced by slits at the polarimeter.
${\mathcal{P}}_{\mathrm{Divergence}}^{\mathrm{Limit}}$
is calculated from the divergence according to Equation (7). For the current record[
Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72], the nominal instrument’s beam divergence was reduced by slits at the polarimeter.

3.4.3 Combined facilities
For the purpose of vacuum birefringence experiments where the background field is generated by an ultra-intense laser and X-ray polarimetry is employed for detection, it is mandatory to combine XFELs with such lasers. In most cases, XFEL facilities host several beamlines and/or several instruments per beamline. Thanks to the wide range of applications and thus an existing market, it is relatively straightforward to equip an XFEL instrument with an ultra-intense laser. Even for systems below the PW level there are enough use cases to use XFELs as probes in laser–matter interactions.
Referring to Table 3, there are three out of four existing hard X-ray facilities equipped with an ultra-intense laser. We can exclude soft X-ray FELs since a key for detection is a short probe wavelength. The facilities and instruments are: MEC at LCLS/SLAC, SACLA EH6 and HED/HIBEF at the European XFEL. Their respective parameters[ Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35, Reference Huang, Deng, Liu, Wang and Zhao91, 98, 111, Reference Nagler, Arnold, Bouchard, Boyce, Boyce, Callen, Campell, Curiel, Galtier, Garofoli, Granados, Hastings, Hays, Heimann, Lee, Milathianaki, Plummer, Schropp, Wallace, Welch, White, Xing, Yin, Young, Zastrau and Lee125– Reference Yabuuchi, Kon, Inubushi, Togahi, Sueda, Itoga, Nakajima, Habara, Kodama, Tomizawa and Yabashi127] are listed in Table 6.
Table 6 Overview of facilities combining XFEL beams with PW-class lasers. Planned facilities are shown in italic. Please note that there is no common factorial relation between laser power and peak intensity. Focusing F-numbers very among the facilities, adapted to their overall mission. Furthermore, beam quality can reduce the encircled energy in the focal spot and therefore reduce the peak intensity[
Reference Yabuuchi, Kon, Inubushi, Togahi, Sueda, Itoga, Nakajima, Habara, Kodama, Tomizawa and Yabashi127]. The provided laser pulse wavefront control for the final focusing and reasonably tight focusing,
![]() ${10}^{22}\ \mathrm{W}/{\mathrm{cm}}^2$
per 1 PW, is realistic.
${10}^{22}\ \mathrm{W}/{\mathrm{cm}}^2$
per 1 PW, is realistic.

The Matter in Extreme Conditions (MEC) instrument is the facility at LCLS that produces extreme matter states with an intense laser radiation, where LCLS provides complete imaging and optical diagnostics methods. Nagler et al.[ Reference Nagler, Arnold, Bouchard, Boyce, Boyce, Callen, Campell, Curiel, Galtier, Garofoli, Granados, Hastings, Hays, Heimann, Lee, Milathianaki, Plummer, Schropp, Wallace, Welch, White, Xing, Yin, Young, Zastrau and Lee125] presented an overview of the beamline, the capabilities of the instrumentation and highlights of experiments. Glenzer et al.[ Reference Glenzer, Fletcher, Galtier, Nagler, Alonso-Mori, Barbrel, Brown, Chapman, Chen, Curry, Fiuza, Gamboa, Gauthier, Gericke, Gleason, Goede, Granados, Heimann, Kim, Kraus, MacDonald, Mackinnon, Mishra, Ravasio, Roedel, Sperling, Schumaker, Tsui, Vorberger, Zastrau, Fry, White, Hasting and Lee130] summarized the first experiment of laser-compressed solids and the measurements of highly accurate X-ray diffraction and X-ray Thomson scattering on the MEC instrument at LCLS. Fletcher et al.[ Reference Fletcher, Curry, Gauthier, Glenn, Chen, Cunningham, Descamps, Frost, Galtier, Heimann, Kim, Mo, Ofori-Okai, Peebles, Seiboth, Treffert, Dyer, McBride and Glenzer131] investigated bremsstrahlung from relativistic electrons generated by the interaction of a high-intensity femtosecond laser with solid μm-thick aluminum and polypropylene targets, and measured the energy spectrum and temperature of hot electrons via differential X-ray energy filtering.
Similar to the LCLS, the SACLA XFEL facility opened after the completion of commissioning[ Reference Yabuuchi, Kon, Inubushi, Togahi, Sueda, Itoga, Nakajima, Habara, Kodama, Tomizawa and Yabashi127, Reference Tono, Togashi, Inubushi, Sato, Katayama, Ogawa, Ohashi, Kimura, Takahashi, Takeshita, Tomizawa, Goto, Ishikawa and Yabashi132]. This experimental platform is equipped with two beams of 800 nm wavelength, 1 Hz repetition rate and 12.5 J maximum energy in a 25 fs pulse duration and a 500 TW peak power after pulse compression. Yabuuchi et al.[ Reference Yabuuchi, Kon, Inubushi, Togahi, Sueda, Itoga, Nakajima, Habara, Kodama, Tomizawa and Yabashi127] characterized the light source performance during the commissioning of the experimental platform and confirmed that the XFEL and the high-intensity laser can operate normally with dedicated diagnostics.
In Europe, the HED scientific instrument at the European XFEL is a unique platform for experiments in extreme conditions of pressure, temperature or electromagnetic field[ Reference Zastrau, Appel, Baehtz, Baehr, Batchelor, Berghäuser, Banjafar, Brambrink, Cerantola, Cowan, Damker, Dietrich, Di Dio Cafiso, Dreyer, Engel, Feldmann, Findeisen, Foese, Fulla-Marsa, Göde, Hassan, Hauser, Herrmannsdörfer, Höppner, Kaa, Kaever, Knöfel, Konôpková, García, Liermann, Mainberger, Makita, Martens, McBride, Möller, Nakatsutsumi, Pelka, Plueckthun, Prescher, Preston, Röper, Schmidt, Seidel, Schwinkendorf, Schoelmerich, Schramm, Schropp, Strohm, Sukharnikov, Talkovski, Thorpe, Toncian, Toncian, Wollenweber, Yamamoto and Tschentscher128, Reference Nakatsutsumi, Appel, Baehtz, Chen, Cowan, Göde, Konopkova, Pelka, Priebe, Schmidt, Sukharnikov, Thorpe, Tschentscher and Zastrau133]. Zastrau et al.[ Reference Zastrau, Appel, Baehtz, Baehr, Batchelor, Berghäuser, Banjafar, Brambrink, Cerantola, Cowan, Damker, Dietrich, Di Dio Cafiso, Dreyer, Engel, Feldmann, Findeisen, Foese, Fulla-Marsa, Göde, Hassan, Hauser, Herrmannsdörfer, Höppner, Kaa, Kaever, Knöfel, Konôpková, García, Liermann, Mainberger, Makita, Martens, McBride, Möller, Nakatsutsumi, Pelka, Plueckthun, Prescher, Preston, Röper, Schmidt, Seidel, Schwinkendorf, Schoelmerich, Schramm, Schropp, Strohm, Sukharnikov, Talkovski, Thorpe, Toncian, Toncian, Wollenweber, Yamamoto and Tschentscher128] presented the scientific scope, technical infrastructure, diagnostics and experimental platforms. The HED scientific instrument supports a variety of X-ray methods, including X-ray polarimetry. The HIBEF user consortium contributes the high-intensity and high-energy laser systems[ Reference Garcia, Höppner, Pelka, Bähtz, Brambrink, Di Dio Cafiso, Dreyer, Göde, Hassan, Kluge, Liu, Makita, Möller, Nakatsutsumi, Preston, Priebe, Schlenvoigt, Schwinkendorf, Šmíd, Talposi, Toncian, Zastrau, Schramm, Cowan and Toncian129, Reference Ahmadiniaz, Bussmann, Cowan, Debus, Kluge and Schützhold134] and their operation for users.
Another combined XFEL–laser facility will be the SEL at SHINE, which is designed to achieve laser intensities sufficient to explore the vacuum birefringence effect by colliding an XFEL[ Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35, Reference King, Hu and Shen135].

Figure 13 Sketch of the experimental setup investigating CRL material properties. The multilayer mirrors collimate the X-rays from the rotating anode X-ray source. The combination of the polarizer, analyzer and charge-coupled device camera allows for polarization sensitive imaging. Reprinted from Ref. [Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61], with the permission of AIP Publishing.
In view of vacuum birefringence, currently operating facilities provide laser intensities of 1019–
![]() ${10}^{21}\ \mathrm{W}/{\mathrm{cm}}^2$
[
Reference Nagler, Arnold, Bouchard, Boyce, Boyce, Callen, Campell, Curiel, Galtier, Garofoli, Granados, Hastings, Hays, Heimann, Lee, Milathianaki, Plummer, Schropp, Wallace, Welch, White, Xing, Yin, Young, Zastrau and Lee125,
Reference Yabuuchi, Kon, Inubushi, Togahi, Sueda, Itoga, Nakajima, Habara, Kodama, Tomizawa and Yabashi127,
Reference Garcia, Höppner, Pelka, Bähtz, Brambrink, Di Dio Cafiso, Dreyer, Göde, Hassan, Kluge, Liu, Makita, Möller, Nakatsutsumi, Preston, Priebe, Schlenvoigt, Schwinkendorf, Šmíd, Talposi, Toncian, Zastrau, Schramm, Cowan and Toncian129]. Thus, ellipticities should be expected to be approximately
${10}^{21}\ \mathrm{W}/{\mathrm{cm}}^2$
[
Reference Nagler, Arnold, Bouchard, Boyce, Boyce, Callen, Campell, Curiel, Galtier, Garofoli, Granados, Hastings, Hays, Heimann, Lee, Milathianaki, Plummer, Schropp, Wallace, Welch, White, Xing, Yin, Young, Zastrau and Lee125,
Reference Yabuuchi, Kon, Inubushi, Togahi, Sueda, Itoga, Nakajima, Habara, Kodama, Tomizawa and Yabashi127,
Reference Garcia, Höppner, Pelka, Bähtz, Brambrink, Di Dio Cafiso, Dreyer, Göde, Hassan, Kluge, Liu, Makita, Möller, Nakatsutsumi, Preston, Priebe, Schlenvoigt, Schwinkendorf, Šmíd, Talposi, Toncian, Zastrau, Schramm, Cowan and Toncian129]. Thus, ellipticities should be expected to be approximately
![]() ${10}^{-14}$
, much smaller than the current best polarization purities. Reasons for those comparably low intensities could be (i) operating at lower energy and power levels due to longer lifetime and cost efficiency, (ii) focusing that is not too tight for target debris management (for laser–matter interactions) and (iii) wavefront distortions re-distributing energy out of the focus peak into a halo.
${10}^{-14}$
, much smaller than the current best polarization purities. Reasons for those comparably low intensities could be (i) operating at lower energy and power levels due to longer lifetime and cost efficiency, (ii) focusing that is not too tight for target debris management (for laser–matter interactions) and (iii) wavefront distortions re-distributing energy out of the focus peak into a halo.
These restrictions can be lifted for experiments dedicated to vacuum birefringence, for example, by providing a dedicated focusing element. We repeat here that a peak intensity of approximately
![]() ${10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
has already been demonstrated with a 4 PW laser system[
Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam109]. That said, the laser at the HED instrument of the European XFEL could reach, with slightly more energy (12.5 J) and shorter pulse duration (25 fs), a peak power of 400 TW and thus approximately
${10}^{23}\ \mathrm{W}/{\mathrm{cm}}^2$
has already been demonstrated with a 4 PW laser system[
Reference Yoon, Kim, Choi, Sung, Lee, Lee and Nam109]. That said, the laser at the HED instrument of the European XFEL could reach, with slightly more energy (12.5 J) and shorter pulse duration (25 fs), a peak power of 400 TW and thus approximately
![]() ${10}^{22}\ \mathrm{W}/{\mathrm{cm}}^2$
peak intensity, resulting in an ellipticity of
${10}^{22}\ \mathrm{W}/{\mathrm{cm}}^2$
peak intensity, resulting in an ellipticity of
![]() $6\times {10}^{-12}$
instead of
$6\times {10}^{-12}$
instead of
![]() $4\times {10}^{-13}$
, as estimated by Mosman and Karbstein[
Reference Mosman and Karbstein85].
$4\times {10}^{-13}$
, as estimated by Mosman and Karbstein[
Reference Mosman and Karbstein85].
3.4.4 X-ray optics
Besides precision X-ray polarizers, CRLs are indispensable optical elements in the vacuum birefringence experimental setup with two purposes. Primarily, the XFEL beam must be focused into the interaction volume with the tightly focused PW laser. This is the purpose of the first CRL. On the other hand, the polarizers require a low divergence to provide a high extinction ratio. Therefore, the first CRLs must be located after the polarizer. In addition, the XFEL must be re-collimated by the second CRL, after the interaction but before the analyzer. In essence, two sets of CRLs are already inside the polarimeter setup. Therefore, the effects of the CRL material on the polarization must be studied and a suitable material must be found. Grabiger et al.[ Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61] studied how the lens material itself influences the X-ray polarization. The setup is shown in Figure 13[ Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61].
Grabiger et al.[ Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61] analyzed three different grades of beryllium samples: high purity (PF-60), optical grade (O-30-H) and ultra-high purity grade (IF-1) beryllium. The results in the upper part of Table 7 clearly indicate that the beryllium samples greatly affect polarization purity. In this regard, the explanation given by the authors is the polycrystalline state of beryllium and they suggested two better options to focus X-rays. One alternative way is to employ reflective optical components, such as Kirkpatrick–Baez mirrors. Another option is to manufacture X-ray lenses from either single-crystal materials such as diamond, or from materials with an amorphous structure, such as glassy carbon and polymers.
Table 7 Deterioration of polarization purity by CRL materials. Upper part for flat Be samples at approximately 8 keV; lower part for CRL telescopes with
![]() $2\times \sim 6\;\mathrm{m}$
focal length at approximately 13 keV. Data taken from Ref. [Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61], with the permission of AIP Publishing, and from Ref. [Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72], licensed under CC BY 4.0.
$2\times \sim 6\;\mathrm{m}$
focal length at approximately 13 keV. Data taken from Ref. [Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61], with the permission of AIP Publishing, and from Ref. [Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72], licensed under CC BY 4.0.

Those materials were studied later by the same group[ Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72]. They now used a synchrotron source for better sensitivity and investigated the impact of CRLs of different materials on the polarization purity, mimicking the general scheme of focusing and re-collimation proposed for vacuum birefringence X-ray polarimetry experiments[ Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey19, Reference Karbstein and Sundqvist33, Reference Shen, Bu, Xu, Xu, Ji, Li and Xu35, Reference Karbstein, Gies, Reuter and Zepf84, Reference Karbstein, Sundqvist, Schulze, Uschmann, Gies and Paulus86]. However, they employed rather long focal lengths of approximately 6 m. For shorter focal lengths, more CRL materials would be exposed to the beam and probably deteriorate the purity more strongly than currently measured. The results are listed in the lower part of Table 7. CRLs were fabricated out of Be, SU-8 photo-polymer, diamond and glassy carbon. From all of those materials, the CRLs fabricated from SU-8 showed the least depolarization of X-rays.
It should be noted that data for Be cannot be easily compared across both parts of Table 7. The effective thickness of the Be CRLs is not provided, and both experiments employed different photon energies.
In regard to X-ray polarimetry for vacuum birefringence, the results show another limit. Even though the deteriorated purity
![]() $\left(3.3\pm 1.5\right)\times {10}^{-11}$
is close to the instrument purity
$\left(3.3\pm 1.5\right)\times {10}^{-11}$
is close to the instrument purity
![]() $\left(1.4\pm 0.9\right)\times {10}^{-11}$
, the deterioration was measurable. Without speculating about scalings, a birefringence experiment using CRLs as currently known would have a limit of at least the measured level of
$\left(1.4\pm 0.9\right)\times {10}^{-11}$
, the deterioration was measurable. Without speculating about scalings, a birefringence experiment using CRLs as currently known would have a limit of at least the measured level of
![]() $\mathcal{P}\sim {10}^{-11}$
. Hence, the prospects for lowering the background signal
$\mathcal{P}\sim {10}^{-11}$
. Hence, the prospects for lowering the background signal
![]() $NT\mathcal{P}$
by better X-ray optics are dismal.
$NT\mathcal{P}$
by better X-ray optics are dismal.
3.5 Interim summary
An attractive application of X-ray polarimetry is to detect the vacuum birefringence phenomenon. There is one widely recognized method, combining PW optical lasers with XFELs. Alternatively two XFEL pulses, out of a pulse train or by a split-and-delay setup, are proposed. Such scheme appears currently more demanding in terms of the X-ray beam path setup.
So far, X-ray polarizer technology has made tremendous progress (cf. Table 5). Material dependencies, beam dependencies (divergence, Equation (7)) and sophisticated alignment protocols (detour avoidance by azimuth alignment) are understood and have become practice. Despite that the transition from synchrotrons to XFELs for polarizer characterization allows for better purity due to the divergence dependence, the spectral width of XFELs is not matching that of polarizers, leading to low throughput. This limits the polarimeter in terms of photon flux: only very few photons arrive at the detector[ Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59]. This can be optimized by spectral tailoring of the FEL process as well as increasing the acceptance of channel-cut crystals by using asymmetric cuts and appropriate polarizer material choice.
That optimization of integrated transmission is mandatory for X-ray polarimetry of vacuum birefringence in order to provide a high-signal photon number
![]() $NT{\delta}^2$
per pulse. Since both the spectral bandwidth of a reflection and the temporal pulse stretching depend on the effective penetration depth, appropriate material selection (high
$NT{\delta}^2$
per pulse. Since both the spectral bandwidth of a reflection and the temporal pulse stretching depend on the effective penetration depth, appropriate material selection (high
![]() $Z$
) could optimize both effects simultaneously. This is in contradiction to high peak reflectivity and the avoidance of detour reflections, which limit the polarization purity
$Z$
) could optimize both effects simultaneously. This is in contradiction to high peak reflectivity and the avoidance of detour reflections, which limit the polarization purity
![]() $\mathcal{P}$
, where it was found that their contribution in the overall reflected beam grows strongly with
$\mathcal{P}$
, where it was found that their contribution in the overall reflected beam grows strongly with
![]() $Z$
.
$Z$
.
It was further recognized that CRL material might affect the polarization purity, as CRLs are foreseen in most schemes for vacuum birefringence. The first investigation of traditional CRL material[ Reference Grabiger, Marx-Glowna, Uschmann, Loetzsch, Paulus and Schulze61] was an important step towards applications of polarimetry, and has shown the need for further investigations and improvements of purity. A follow-up study, employing actual CRL telescopes (as often proposed for vacuum birefringence studies) fabricated from unconventional materials, showed that those materials have a much reduced impact on the purity[ Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72].
As this impact is probably limiting the purity
![]() $\mathcal{P}$
, the ratio of signal to background,
$\mathcal{P}$
, the ratio of signal to background,
![]() ${\delta}^2/\mathcal{P}$
, must be improved by increasing the ellipticity
${\delta}^2/\mathcal{P}$
, must be improved by increasing the ellipticity
![]() ${\delta}^2$
. This is possible due to the strong scaling with laser peak intensity,
${\delta}^2$
. This is possible due to the strong scaling with laser peak intensity,
![]() ${\delta}^2\propto {I}_{\mathrm{BG}}^2$
(cf. Equation (16a)). Thereby, also the absolute signal photon number
${\delta}^2\propto {I}_{\mathrm{BG}}^2$
(cf. Equation (16a)). Thereby, also the absolute signal photon number
![]() $NT{\delta}^2$
increases, reducing the number of required laser pulses.
$NT{\delta}^2$
increases, reducing the number of required laser pulses.
In summary, measurements of vacuum birefringence in laboratory conditions from ultra-intense lasers by X-ray polarimetry are still pending and need proper preparation in regard to source photon count, beam divergence, spectral transmission, polarizer reflectivity, CRL transmission and depolarization, polarizer extinction and detector efficiency.
4 Further applications of X-ray polarimetry
Apart from probing vacuum birefringence, X-ray polarimetry is applied to other scientific cases: nuclear resonant scattering experiments[ Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68, Reference Baron, Tanaka, Goto, Takeshita, Matsushita and Ishikawa136– Reference Toellner, Alatas and Said138], measuring the magnetic fields inside solid-density plasmas via Faraday rotation[ Reference Huang, Schlenvoigt, Takabe and Cowan139– Reference Wang, Toncian, Wei and Arefiev141] and applications to astrophysics[ Reference Heyl and Caiazzo34, Reference Caiazzo and Heyl82, Reference Schnittman and Krolik142, Reference Krawczynski, Matt, Ingram, Taverna, Turolla, Kislat, Cheung, Bykov, Sinha, Zhang, Heyl, Bucciantini, Madejski, Kallman, Jahoda, Abarr, Baring, Baldini, Begelman, Boettcher, Cackett, Caiazzo, Coppi, Costa, Dexter, Fortin, Gammie, Gaskin, Giannios, Ghosh, Harding, Hartmann, Hayashida, Jorstad, Kaaret, Kitaguchi, Latronico, Maccarone, Marscher, Marshall, McConnell, Miller, O’Dell, Oezel, Okajima, Pearce, Perkins, Ramsey, Romani, Schnittman, Sgro, Soffitta, Takahashi, Tamagawa, Tomsick, Weisskopf and Younes143]. Now, we present those applications of X-ray polarimetry.
4.1 Nuclear resonant scattering
Nuclear resonant scattering is a technique for measuring the structural dynamics, magnetic and electronic properties of condensed matter. Compared to the usual radioactive sources, synchrotron radiation sources open up new perspectives for nuclear resonant scattering in the field of materials science[
Reference Toellner, Alp, Sturhahn, Mooney, Zhang, Ando, Yoda and Kikuta67,
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68,
Reference Gerdau, Rüffer, Winkler, Tolksdorf, Klages and Hannon144]. Polarimetry with perfect crystals is adequate for preventing the non-resonant scattering called polarization filtering in nuclear resonant scattering experiments[
Reference Toellner, Alp, Sturhahn, Mooney, Zhang, Ando, Yoda and Kikuta67,
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68,
Reference Röhlsberger, Gerdau, Rüffer, Sturhahn, Toellner, Chumakov and Alp145]. The elementary idea is to separate non-resonant scattering from a large background of resonantly scattered X-rays. The schematic setup is displayed in Figure 14[
Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68]. The polarizer and analyzer are silicon (840) channel-cut crystals with two asymmetric reflections and are in the crossed position. Linearly polarized radiation will switch its polarization to mix polarization states when it is scattered by a medium placed in a magnetic field upon nuclear resonant reflection.
![]() $\pi$
-components can pass through but
$\pi$
-components can pass through but
![]() $\sigma$
-components are strongly suppressed by the analyzer in the crossed position. Thereby, the pump photons can be sufficiently suppressed while the relatively weak signal can be detected.
$\sigma$
-components are strongly suppressed by the analyzer in the crossed position. Thereby, the pump photons can be sufficiently suppressed while the relatively weak signal can be detected.

Figure 14 Schematic setup for nuclear resonant scattering with the polarization filtering method. The incoming radiation from the left is polarized by the first channel-cut crystal. Subsequently, the beam impinges on the magnetically anisotropic sample under investigation. The green arrow indicates the direction of the external magnetic field that induces optical activity via X-ray magnetic linear dichroism. The analyzer crystal in the crossed setting transmits only the photons that have undergone nuclear resonant
![]() $\sigma$
- to
$\sigma$
- to
![]() $\pi$
–scattering. Taken from Ref. [Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68], licensed under CC BY 4.0.
$\pi$
–scattering. Taken from Ref. [Reference Marx-Glowna, Uschmann, Schulze, Marschner, Wille, Schlage, Stöhlker, Röhlsberger and Paulus68], licensed under CC BY 4.0.
4.2 Detection of magnetic fields
In 1990, Siddons et al.[ Reference Siddons, Hart, Amemiya and Hastings16] observed the rotation of the polarization plane of a synchrotron X-ray beam in cobalt alloys by X-ray polarimetry, thereby detecting the optical Faraday effect in the X-ray domain. They also demonstrated the optical activity near the K-edge of cobalt in a chiral organometallic compound.
Faraday rotation is also a widely used diagnostic of plasmas[ Reference Hutchinson146, Reference Segre147], usually employing visible lasers in low-density plasmas, for example, magnetic confinement fusion plasmas[ Reference Pisarczyk, Rupasov, Sarkisov and Shikanov148]. With XFELs, this method can be transferred to solid-density plasmas. This is of great interest for plasmas driven by ultra-short ultra-intense lasers to probe self-generated magnetic fields[ Reference Huang, Schlenvoigt, Takabe and Cowan139]. The fields reach kilo- to megatesla (MT)-level field strength and originate from fast electron transport, balancing return currents and their respective resistivity inside the solid target[ Reference Wang, Toncian, Wei and Arefiev141]. Researchers[ Reference Huang, Schlenvoigt, Takabe and Cowan139– Reference Wang, Toncian, Wei and Arefiev141] have proposed a method of examining the magnetic fields of the laser-irradiated plasma by X-ray polarimetry via Faraday rotation using XFELs.

Figure 15 An illustrated experimental setup of strong magnetic field generation by interaction of an ultra-short relativistic optical laser pulse with solid matter, probed by an XFEL via Faraday rotation. Taken from Ref. [Reference Huang, Takabe and Cowan140], licensed under CC BY 4.0.
Figure 15 depicts the experimental setup[ Reference Huang, Takabe and Cowan140]. The optical ultra-short relativistic laser pulse is deployed to generate extreme multi-megagauss (MG) magnetic fields in a solid-density target. The XFEL acts as a probe to detect those laser-driven magnetic fields. The probe XFEL beam is perfectly horizontally polarized, and then the orientation of the polarization plane is rotated by the magnetic field component. The total rotation angle of the exiting XFEL beam is as follows[ Reference Huang, Schlenvoigt, Takabe and Cowan139, Reference Huang, Takabe and Cowan140]:
with
![]() ${e}_0$
being the electron’s charge,
${e}_0$
being the electron’s charge,
![]() $c$
the speed of light,
$c$
the speed of light,
![]() ${m}_{\mathrm{e}}$
the electron’s rest mass,
${m}_{\mathrm{e}}$
the electron’s rest mass,
![]() $\int \mathrm{d}s$
the integral along the probe beam path,
$\int \mathrm{d}s$
the integral along the probe beam path,
![]() ${n}_{\mathrm{e}}$
the electron density and
${n}_{\mathrm{e}}$
the electron density and
![]() $\mathbf{k}$
the wave vector of the probe. The critical density
$\mathbf{k}$
the wave vector of the probe. The critical density
![]() ${n}_{\mathrm{c}}$
is defined by the following:
${n}_{\mathrm{c}}$
is defined by the following:
 $$\begin{align}{n}_{\mathrm{c}}=\frac{\varepsilon_0\kern0.1em {m}_{\mathrm{e}}\kern0.1em {\omega}^2}{e_0^2}=\frac{\varepsilon_0\kern0.1em {m}_{\mathrm{e}}\kern0.1em 4{\pi}^2\kern0.1em {c}^2}{e_0^2\kern0.1em {\lambda}^2},\end{align}$$
$$\begin{align}{n}_{\mathrm{c}}=\frac{\varepsilon_0\kern0.1em {m}_{\mathrm{e}}\kern0.1em {\omega}^2}{e_0^2}=\frac{\varepsilon_0\kern0.1em {m}_{\mathrm{e}}\kern0.1em 4{\pi}^2\kern0.1em {c}^2}{e_0^2\kern0.1em {\lambda}^2},\end{align}$$
being the highest electron density in which a wave with wavelength
![]() $\lambda =2\pi /\mid \mathbf{k}\mid$
can propagate.
$\lambda =2\pi /\mid \mathbf{k}\mid$
can propagate.
From Equations (19) and (20) we can see that the rotation angle is proportional to the wavelength of the probe beam. A beam with a long wavelength can obtain a large rotation angle but will have poor penetration depth in solid-density plasma. However, even though the wavelength of the XFEL is short, the XFEL is able to penetrate solid-density plasmas of up to several tens of micrometers thicknesses because of the high attenuation length. Therefore, it is advantageous to select the XFEL beam as the probe pulse. Studies proposing this scheme[
Reference Huang, Schlenvoigt, Takabe and Cowan139,
Reference Wang, Toncian, Wei and Arefiev141] estimate that the polarization of an XFEL with 6.457 keV photon energy will be rotated about
![]() $\pm 300\;\unicode{x3bc} \mathrm{rad}$
. The two signs arise from the symmetry to the electron current axis where fields are parallel or anti-parallel to the probe beam direction. An order of
$\pm 300\;\unicode{x3bc} \mathrm{rad}$
. The two signs arise from the symmetry to the electron current axis where fields are parallel or anti-parallel to the probe beam direction. An order of
![]() ${10}^{-4}$
rad does not require the utmost polarization purity, in contrast to vacuum birefringence. Nevertheless, for an imaging application, overall transmission is important due to beam size magnification.
${10}^{-4}$
rad does not require the utmost polarization purity, in contrast to vacuum birefringence. Nevertheless, for an imaging application, overall transmission is important due to beam size magnification.
4.3 Astrophysics
X-ray polarimetry is an appealing tool to investigate geometric information, emission mechanisms and the structure of the magnetic fields in and around objects in the universe, such as supermassive black holes and neutron stars[ Reference Heyl and Caiazzo34, Reference Caiazzo and Heyl82, Reference Schnittman and Krolik142, Reference Krawczynski, Matt, Ingram, Taverna, Turolla, Kislat, Cheung, Bykov, Sinha, Zhang, Heyl, Bucciantini, Madejski, Kallman, Jahoda, Abarr, Baring, Baldini, Begelman, Boettcher, Cackett, Caiazzo, Coppi, Costa, Dexter, Fortin, Gammie, Gaskin, Giannios, Ghosh, Harding, Hartmann, Hayashida, Jorstad, Kaaret, Kitaguchi, Latronico, Maccarone, Marscher, Marshall, McConnell, Miller, O’Dell, Oezel, Okajima, Pearce, Perkins, Ramsey, Romani, Schnittman, Sgro, Soffitta, Takahashi, Tamagawa, Tomsick, Weisskopf and Younes143, Reference Weisskopf, Cohen, Kestenbaum, Long, Novick and Wolff149]. In astrophysics, the formation and subsequent evolution of the population of black holes are fascinating and can be determined by the mass and angular momentum given by X-ray polarimetry[ Reference Schnittman and Krolik142]. In 1976, Weisskopf et al.[ Reference Weisskopf, Cohen, Kestenbaum, Long, Novick and Wolff149] measured the linear polarization of the X-ray flux from the Crab Nebula by the graphite crystal X-ray polarimeters aboard the OSO-8 satellite, as illustrated in Figure 16[ Reference Weisskopf, Cohen, Kestenbaum, Long, Novick and Wolff149]. For reducing the background signal from cosmic rays, the parabolic surface is used to focus the diffracted X-rays. Caiazzo and Heyl[ Reference Caiazzo and Heyl82] showed that vacuum birefringence affects changes of the X-ray polarization of stellar-mass and supermassive black holes. The model with QED can not only probe the spin and the magnetic field strength close to the innermost stable orbit of black-hole accretion disks, but also provides a validity check for theories of astrophysical accretion. For accretion-powered pulsars with known energy of cyclotron-resonant scattering features[ Reference Weisskopf, Elsner, Kaspi, ODell, Pavlov and Ramsey150], X-ray polarimetry is suited to obtain information about the geometry of the accretion column and magnetic field strength. Besides, X-ray polarimetry has the potential to discover the mechanisms of astrophysical particle acceleration, such as supernova remnants (SNRs), pulsar wind nebulae (PWNe), pulsars and black-hole jets[ Reference Krawczynski, Matt, Ingram, Taverna, Turolla, Kislat, Cheung, Bykov, Sinha, Zhang, Heyl, Bucciantini, Madejski, Kallman, Jahoda, Abarr, Baring, Baldini, Begelman, Boettcher, Cackett, Caiazzo, Coppi, Costa, Dexter, Fortin, Gammie, Gaskin, Giannios, Ghosh, Harding, Hartmann, Hayashida, Jorstad, Kaaret, Kitaguchi, Latronico, Maccarone, Marscher, Marshall, McConnell, Miller, O’Dell, Oezel, Okajima, Pearce, Perkins, Ramsey, Romani, Schnittman, Sgro, Soffitta, Takahashi, Tamagawa, Tomsick, Weisskopf and Younes143]. Heyl and Caiazzo[ Reference Heyl and Caiazzo34] applied the equation of the polarization evolution to determine the atmosphere composition and the surface gravity of an X-ray pulsar. Furthermore, the radius of the star can be inferred from the photon energy at the polarization direction flips. Therefore, X-ray polarimetry is a powerful tool to study neutron stars and black holes. Its high sensitivity and resolution are promising to unravel crucial information of the physical processes and structure of astronomical objects.

Figure 16 Exploded view of the OSO-8 polarimeter assemblies. The crystal reflector employs approximately
![]() $45{}^{\circ}$
Bragg angle and is thereby polarization-filtering. Reprinted from Ref. [Reference Novick151], with the permission of Springer Nature.
$45{}^{\circ}$
Bragg angle and is thereby polarization-filtering. Reprinted from Ref. [Reference Novick151], with the permission of Springer Nature.
5 Conclusions
This paper reviews the status of X-ray polarimetry and mainly its application for detecting vacuum birefringence. First, the main details of the factors affecting the polarization purity of X-rays were analyzed for 45° Bragg reflectors, employing Brewster’s law for suppression of a linear component in the plane of incidence. Crystal quality, beam quality and material dependencies were presented and detailed for channel-cut crystal polarizers. An unprecedented polarization purity of
![]() $1.4\times {10}^{-11}$
has been measured so far[
Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72] at a synchrotron thanks to the average high flux, such that divergence reduction still allowed for precise measurements. A measurement at an XFEL yielded
$1.4\times {10}^{-11}$
has been measured so far[
Reference Marx-Glowna, Grabiger, Lötzsch, Uschmann, Schmitt, Schulze, Last, Roth, Antipov, Schlenvoigt, Sergueev, Leupold, Röhlsberger and Paulus72] at a synchrotron thanks to the average high flux, such that divergence reduction still allowed for precise measurements. A measurement at an XFEL yielded
![]() $8\times {10}^{-11}$
[
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59]. There, the divergence would have allowed for
$8\times {10}^{-11}$
[
Reference Schulze, Grabiger, Loetzsch, Marx-Glowna, Schmitt, Garcia, Hippler, Huang, Karbstein, Konôpková, Schlenvoigt, Schwinkendorf, Strohm, Toncian, Uschmann, Wille, Zastrau, Röhlsberger, Stöhlker, Cowan and Paulus59]. There, the divergence would have allowed for
![]() ${10}^{-14}$
, yet the setup was not as optimized as at the synchrotron, and the effective flux was insufficient for precise characterization. However, the record at the synchrotron is limited by the divergence, and substantial future improvements are subject to XFELs.
${10}^{-14}$
, yet the setup was not as optimized as at the synchrotron, and the effective flux was insufficient for precise characterization. However, the record at the synchrotron is limited by the divergence, and substantial future improvements are subject to XFELs.
This high level of polarization purity provides an opportunity to explore the nonlinear property of vacuum, such as vacuum birefringence. An all-optical laboratory scheme allows for precise measurements of QED nonlinearities in particular in the low-energy but strong-field limit, which is sensitive to new physics and particles beyond the standard model[
Reference Gies21,
Reference Hill and Roso38]. For this application, we summarized for various proposals the signal dependence on ultra-intense laser sources that offer extremely intense external fields to polarize the vacuum. We presented the scientific facilities of optical PW lasers and XFELs throughout the world. We assessed their status regarding proposed experimental schemes and added aspects beyond the sole polarization purity
![]() $\mathcal{P}$
and ellipticity
$\mathcal{P}$
and ellipticity
![]() ${\delta}^2$
, relevant in the entirety of the proposed schemes. What is more, the X-ray polarimetry has a wide range of applications in nuclear resonant scattering experiments and measuring the magnetic fields inside solid-density plasmas, even astrophysics. In brief, X-ray polarimetry is an extraordinary method and it provides scientists with the possibility to explore the unknown.
${\delta}^2$
, relevant in the entirety of the proposed schemes. What is more, the X-ray polarimetry has a wide range of applications in nuclear resonant scattering experiments and measuring the magnetic fields inside solid-density plasmas, even astrophysics. In brief, X-ray polarimetry is an extraordinary method and it provides scientists with the possibility to explore the unknown.
Acknowledgements
The author Qiqi Yu would like to thank the China Scholarship Council for financial support (No. 201908310159). The support of the High Energy Density Department at Helmholtz-Zentrum Dresden – Rossendorf is gratefully acknowledged. The authors thank the Ministry of Science and Technology of the People’s Republic of China (Grant No. 2018YFA0404803) and the National Natural Science Foundation of China (Grant No. 11935008). We would like to thank Kai Sven Schulze, Robert Loetzsch, Berit Marx-Glowna, Ingo Uschmann, Gerhard G. Paulus, Felix Karbstein, Holger Gies, Lingen Huang, Jörg Grenzer and Roland Sauerbrey for fruitful discussions.