1 Introduction
Ultra-short and broadband laser sources are formidable tools for a wide range of scientific areas. In the field of ultrafast science, laser pulses lasting only a few optical cycles are used to generate secondary sources, such as soft X rays via high harmonic generation[Reference Holgado, Hernández-García and Alonso1], attosecond pulses[Reference Ren, Li and Yin2] and terahertz radiation, which within their many applications can be adopted in probing matter at atomic scales[Reference Li, Zhou and Lock3]. Such sources are also widely explored in applications in ultrafast spectroscopy[Reference Pastorczak, Nejbauer and Radzewicz4], pump-probes in chemistry[Reference Neri, Donaldson and Cowan5], condensed matter and optical coherence tomography[Reference Nishizawa, Kawagoe, Yamanaka, Matsushima, Mori and Kawabe6], among many other fields. Simultaneously, ultra-short, high-energy intense sources enable the study of astrophysical phenomena in laboratories[Reference Rigby, Cruz and Albertazzi7], contribute to advances in several high-field physics topics and are used in particle acceleration schemes[Reference Bartal, Foord and Bellei8].
Over the past three decades, Ti:sapphire- and Nd:glass-based laser systems have been the regular workhorses for reliably generating energetic ultra-short pulses, supporting sub-100 fs durations and energies up to hundreds of joules[Reference Sung, Lee, Yu, Jeong and Lee9, Reference Gaul, Martinez and Blakeney10]. The main drawbacks of these well-performing setups are their restricted tunability, limited spectral bandwidth, amplified spontaneous emission and low repetition rates: kilohertz for Ti:sapphire and sub-hertz for Nd:glass. These limitations are significant hindrances currently limiting their performance and preventing them from reaching multi-petawatt regimes with high repeatability.
A widely-used amplification technique that allows the overcoming of the tunability and spectral bandwidth issues faced by conventional laser amplification is optical parametric chirped pulse amplification (OPCPA)[Reference Dubietis, Jonusauskas and Piskarskas11, Reference Ross, Matousek, Towrie, Langley and Collier12], which combines the chirped pulse amplification (CPA)[Reference Strickland and Mourou13] and optical parametric amplification (OPA) techniques. Optical parametric chirped pulse amplification enables ultra-short (few-femtosecond) pulse amplification with high single-pass gain[Reference Musgrave, Shaikh and Galimberti14], high contrast and no critical thermal effects, allowing the development of ultra-broadband, few-cycle sources and multi-petawatt peak-power laser systems[Reference Zhu, Xie and Sun15]. However powerful the OPCPA concept may be, it also presents some challenges: the pump and signal pulses require precise and stable temporal matching and synchronization; the pump beam must possess spatial uniformity in order to obtain a homogeneous spatial gain; and there exist currently a very limited number of nonlinear crystals with sufficient aperture for high-energy stages that fulfill the phase-matching conditions to a degree that enables broad bandwidth amplification.
For low-energy amplification stages (such as the front-end of high-energy systems), beta-barium borate (BBO)[16, Reference Schultze, Binhammer, Steinmann, Palmer, Emons and Morgner17] and lithium triborate (LBO)[Reference Zhu, Xie and Sun15, Reference Xu, Yu and Liang18, Reference Tang, Ross and Hernandez-Gomez19] are two of the most widely used crystals. They possess relatively high nonlinear coefficients (~picometers per volt) and broad gain bandwidths (hundreds of nanometers).
Broadband operation using BBO pumped by tens of microjoules with kilohertz-to-megahertz repetition rate pulses was shown by Andersen et al. and other groups[Reference Schultze, Binhammer, Steinmann, Palmer, Emons and Morgner17, Reference Andersen, Schmidt and Bruchmann20]. These systems deliver microjoule pulses with ~200 nm (1/e 2 width) of amplified spectrum centered at ~900 nm. Meanwhile, broadband capability was also shown with LBO by different groups[Reference Zhu, Xie and Sun15, Reference Zhao, Jiang, Sueda, Miyanaga and Kobayashi21, Reference Galletti, Archipovaite, Oliveira, Galimberti, Musgrave and Hernandez-Gomez22] in the spectral range studied. The systems, pumped by microjoule-to-joule pulses at kilohertz-to-hertz repetition rates, deliver microjoule-to-joule pulses with ~200 nm (1/e 2 width) or less.
Meanwhile, for high-energy stages there are only a few crystals that can be implemented in view of the large apertures and tens of centimeter length required[Reference Zhu, Xie and Sun15]. Among these are potassium dihydrogen phosphate (KDP) crystals, potassium dideuterium phosphate crystals and isomorphs (KD*P, DKDP)[Reference Galimberti, Hernandez-Gomez, Musgrave, Ross and Winstone23] or LBO crystals. However, they have the drawback of a low nonlinear coefficient. In this context, alternative solutions for high-power, ultra-short pulse operation are highly desirable.
In this work, we evaluate the performance of two alternative crystals for both low- and high-energy, few-cycle OPCPA: bismuth borate (BiB3O6 or BiBO) and yttrium calcium oxyborate (YCa4O(BO3)3 or YCOB). In particular, we have developed a noncollinear optical parametric amplification (NOPA) setup, operating in the near-infrared (IR) region, in order to test the performance of each crystal. We obtained for a 5 mm YCOB crystal an amplified bandwidth of 200 nm and a gain of ~102, and for a 2.5 mm BiBO crystal an amplified bandwidth of 240 nm and a gain of ~103. These results are analyzed in the context of numerical simulations using an in-house developed code[Reference Galimberti, Hernandez-Gomez, Musgrave, Ross and Winstone23].
To the best of our knowledge, this is the first demonstration of both ultra-broadband OPA in BiBO in the near-IR wavelength range and the broadest bandwidth obtained using YCOB.
These results are therefore of high interest to the laser developer community, highlighting promising alternatives to the commonly used nonlinear crystals.
Due to its size, YCOB can be implemented in high-energy, long-pulse (nanosecond) regime NOPA stages with comparable performance, both in bandwidth and efficiency, to the commonly used LBO and KDP crystals in the near-IR regime where high-power laser systems usually operate.
Meanwhile, BiBO can be advantageously adopted in low-energy, high repetition rate, few-cycle or femtosecond/picosecond stages (within high-power systems), showing superior performance when compared to BBO or LBO crystals in the near-IR regime. This capability is also critical for multi-stage systems where preservation of the ultra-broad bandwidths involved is essential for further efficient high-power amplification.
In the past two decades, several crystals have emerged as promising nonlinear media for ultra-broadband OPA. In this section we review the properties of two of those, namely YCOB and BiBO.
1.1 Yttrium calcium oxyborate
Yttrium calcium oxyborate was first identified in 2000, and extensive studies have been performed[24–26] identifying its potential as an addition to the oxyborate crystal family. Yttrium calcium oxyborate is a biaxial crystal featuring several optical, thermal and mechanical properties that make it attractive for OPA applications. It possesses a high nonlinear coefficient (up to 1.4 pm/V in the near-IR), larger than that of DKDP and even LBO. While BBO has a higher coefficient, its size is currently limited to the single-centimeter scale, preventing its use with high-energy pulses. Yttrium calcium oxyborate, on the other hand, can be grown to large sizes (75 mm × 75 mm aperture by 25 cm length) while having a high damage threshold (≈15 J/cm2 at 800 nm wavelength)[Reference Pires, Galimberti and Figueira27, Reference Liao, Jovanovic, Ebbers, Fei and Chai28]. Moreover, it allows operation over a larger temperature range, has a small dispersion angle and allows a shorter growth period by the Czochralski method[Reference Friedrich29], leading to cost-efficient manufacture. Besides this, it exhibits a large angular acceptance for phase matching and small beam walk-off. All of these properties made YCOB one of the leading candidates for high average power operation.
1.2 Bismuth borate
Bismuth borate is a biaxial nonlinear crystal with unique optical properties for frequency conversion at the visible and ultraviolet frequencies[Reference Ghotbi and Ebrahim-Zadeh30, Reference Ghotbi, Ebrahim-Zadeh, Majchrowski, Michalski and Kityk31] that has recently seen a surge of interest. It combines the mechanical, thermal and optical advantages of well-known materials, such as BBO, with higher optical nonlinearity (≈3 pm/V) than any other crystal usable in the near-IR. It allows flexible phase-matching geometries[Reference Petrov, Ghotbi and Kokabee32] due to its large range of phase-matching angles and possesses good thermo-optical properties, similar to YCOB. The main drawback of this crystal is its large walk-off angle, limiting its use to small thicknesses. Bismuth borate is widely used in the optical parametric oscillator (OPO)/OPA community, establishing it as an optimal candidate for low-energy, high-repetition rate and broadband operation[32–34].
2 Ultra-broadband OPA stage design
To amplify a substantial spectral portion of the super-continuum, a noncollinear interaction geometry is required. We used in-house developed software[Reference Galimberti, Hernandez-Gomez, Musgrave, Ross and Winstone23, Reference Pires, Galimberti and Figueira27] based on the three-wave-mixing approach (see Equation (1) below), adopting the Sellmeier equations (shown in Table 1) and the well-known Fresnel equation, in order to estimate the parameters of the noncollinear ultra-broadband amplification stage, such as the phase-matching angle for collinear operation θ C, crystal orientation angle ϕ, the index of refraction for each wavelength involved and the noncollinear angle θ NC as in Equation (2).
Table 1 Sellmeier equation (
${n}_i^2=A+B/\left({\lambda}^2-C\right)-D{\lambda}^2$
) coefficients for YCOB and BiBO[Reference Pires, Galimberti and Figueira27, Reference Umemura, Miyata and Kato35].
In the case of YCOB, interaction geometries outside of the principal planes are used to also maximize the nonlinear coefficient d eff[Reference Pires, Galimberti and Figueira27], and correspondingly the parametric gain, while enabling broadband amplification.
The simulations rely on solving the three-wave mixing coupled equations for optical parametric processes. In the software that we developed, the system of equations is solved for the envelope of the fields in a plane wave scenario, and it does not take into account spatial effects like diffraction or birefringence, nor high-order temporal effects such as cascaded nonlinear effects. The only spatial effect taken into account is the walk-off, which, although being a 2D effect, may be inserted as a lossy term[Reference Galletti, Pires and Hariton36, Reference Gale, Cavallari and Hache37], with its coefficient estimated as
$$\begin{align*}{\alpha}_{{\mathrm{w}}_{\mathrm{s},\mathrm{i}}}=\frac{1}{l_{{\mathrm{w}}_{\mathrm{s},\mathrm{i}}}}=\frac{\rho_{\mathrm{w}}}{\sqrt{\pi}{R}_{\mathrm{s},\mathrm{i}}},\end{align*}$$
where 
${l}_{w_{\mathrm{s},\mathrm{i}}}$
is the walk-off length, ρ w is the walk-off angle and R s,i is the radius of the signal-idler beam.
The system of equations[Reference Sutherland38] solved is
$$\begin{align}\frac{\partial {A}_{\mathrm{p}}}{\partial z}+\frac{\kern0.24em \partial {A}_{\mathrm{p}}}{v_{\mathrm{p}}\partial t}& = i\;{K}_{\mathrm{p}}\;{A}_{\mathrm{i}}\;{A}_{\mathrm{s}}\;\exp \left(i\Delta kz\right),\nonumber\\ {}\frac{\partial {A}_{\mathrm{s}}}{\partial z}+\frac{\kern0.24em \partial {A}_{\mathrm{s}}}{v_{\mathrm{s}}\partial t}-{\alpha}_{{\mathrm{w}}_{\mathrm{s},\mathrm{i}}}{A}_{\mathrm{s}}& = i\;{K}_{\mathrm{s}}\;{A}_{\mathrm{p}}\;{A}_{\mathrm{i}}^{\ast}\;\exp \left(-i\Delta kz\right), \nonumber\\ {}\frac{\partial {A}_{\mathrm{i}}}{\partial z}+\frac{\kern0.24em \partial {A}_{\mathrm{i}}}{v_{\mathrm{i}}\partial t}-{\alpha}_{{\mathrm{w}}_{\mathrm{s},\mathrm{i}}}{A}_{\mathrm{i}}& = i\;{K}_{\mathrm{i}}\;{A}_{\mathrm{p}}\;{A}_{\mathrm{s}}^{\ast}\;\exp \left(-i\Delta kz\right),\end{align}$$
where the subscripts p, s and i stand for pump, signal and idler, respectively,
$$\begin{align*}{K}_{\mathrm{p},\mathrm{s},\mathrm{i}}=\frac{2\pi {d}_{\mathrm{eff}}}{n_{\mathrm{p},\mathrm{s},\mathrm{i}}{\lambda}_{\mathrm{p},\mathrm{s},\mathrm{i}}},\end{align*}$$
where λ p,s,i is the wavelength, n p,s,i is the refractive index, v p,s,i is the group velocity, ∆k is the phase mismatch and z is the propagation direction. Note that this system of equations takes into account both temporal and spatial walk-off. Regarding the phase matching, as shown in Figure 1, a noncollinear scenario is assumed with
\begin{align}\Delta k={k}_{\mathrm{p}}\cos {\theta}_{\mathrm{NC}}-{k}_{\mathrm{s}}-{k}_{\mathrm{i}}\cos\, \varOmega \end{align}
where the two angles are given by
$$\begin{align*}\begin{array}{r@{}c@{}l}&&\cos\, \varOmega \;=\;\; \displaystyle\frac{v_{\mathrm{s}}}{v_{\mathrm{i}}},\\ {}{\theta}_{\mathrm{NC}} & \;=\;\;& \arcsin \left(\displaystyle\frac{k_{\mathrm{i}}}{k_{\mathrm{p}}}\sin\, \varOmega \right), \end{array}\end{align*}$$
where k i and k p are the wavevectors for the idler and the pump, respectively. The routine was benchmarked with the well-known three-wave mixing (TWM)/OPA software SNLO[Reference Galletti, Pires and Hariton36] and chi2D[Reference Lang, Harth, Matyschok, Binhammer, Schultze and Morgner39].
Using our code we performed a parametric scan regarding the signal central wavelength (Figure 2(a)) and the noncollinear angle (Figure 2(b)) on the BiBO crystal to find the appropriate parameters to maximize the OPA stage performance.
Figure 1 Representation of noncollinear phase-matching condition. o.a. is the crystal optic axis.
Figure 2 Parametric scan for the BiBO nonlinear crystal. (a) Simulated phase-matched wavelength (λ sM) dependence of the amplified spectrum. The crystal thickness is 2.5 mm and the pump intensity is ~50 GW/cm2. (b) Simulated noncollinear angular dependence of the amplified spectrum over a range ~1.6. The crystal thickness is 2.5 mm and the pump intensity is ~50 GW/cm2. The box (translucent white) highlights the region of interest where the bandwidth is maximized but the central region (~0.9 μm) is not heavily depleted.
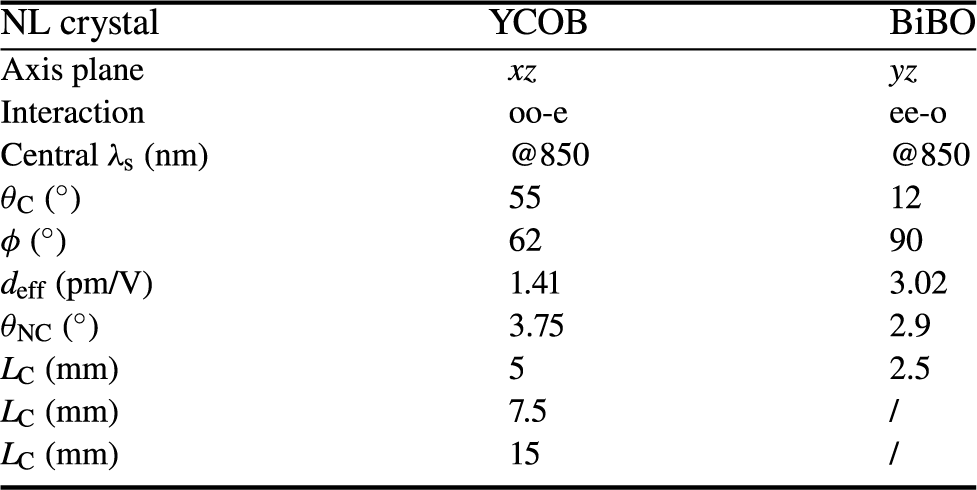
Taking into consideration the results of the parametric scan for the BiBO crystal and the theoretical study performed by Pires et al. [Reference Pires, Galimberti and Figueira27] (and validated by our code and the chi2D code[Reference Lang, Harth, Matyschok, Binhammer, Schultze and Morgner39]) for the YCOB crystal, we performed conclusive simulations for the OPA stages. We considered the same pump source as for the experimental setup (described in Section 3) and optimized numerically the values of θ C, ϕ C and θ NC that maximize the nonlinear coefficient d eff (and correspondingly the parametric gain) while enabling broadband amplification. The retrieved parameters for the crystals used in the implementation of the OPA stage are detailed in Table 2. For YCOB, we tested three crystals with lengths 5 mm, 7.5 mm and 15 mm, all other parameters being the same. Figures 3 and 4 show the calculated amplified spectrum for each case.
Table 2 Parameters for the nonlinear crystals BiBO and YCOB to obtain broadband amplification. θ C (°) and ϕ (°) are the crystal angles for perfect phase matching, d eff (pm/V) is the nonlinear efficiency, θ NC (°) is the noncollinear angle and L C (mm) is the crystal length.
3 Experimental setup
This work was performed in the framework of the development of an OPCPA laser chain installed at the Laboratory for Intense Lasers (L2I) at Instituto de Plasmas e Fusão Nuclear (IPFN) in Lisbon. In this context the optimal performance of OPCPA crystals aiming to provide ultra-broadband pulses at the sub-millijoule level was studied. Focus was given to BiBO due to the previously observed very high efficiencies[Reference Galletti, Pires and Hariton36], and to YCOB due to the capability of scaling to very large energies[Reference Pires, Galimberti and Figueira27].
The experimental setup (Figure 5) is centered on a home-built, Ti:sapphire-seeded Yb:CaF2 regenerative amplifier[Reference Joao, Pires, Cardoso, Imran and Figueira40] operating at 160 Hz and delivering 2.2 mJ pulses at 1030 nm. A fraction of the pulse energy (1.7 mJ) is compressed down to 700 fs using a grating compressor with 70% efficiency. Both pump and signal beams of the NOPA stage are generated by splitting the former beam. The signal is obtained by focusing 0.35 mJ of the pulse energy in a 4 mm sapphire plate to generate an intrinsically chirped super-continuum spanning the 540–1050 nm spectral range as shown in Figure 6. The process is tuned to allow a stable, relatively smooth and ultra-broadband spectrum [41] although with extremely low efficiencies, yielding an output energy estimated at the few-nanojoule level, below the measurement range of the diagnostics used. For contrast reasons, an edge pass filter was used to suppress the fundamental beam at 1030 nm. The remaining 0.8 mJ of the compressed pulses is frequency-doubled to 515 nm in a BBO crystal with an efficiency of 50%, and it is used as the pump for the ultrafast (sub-picosecond) OPCPA chain, as mentioned in Section 1.
Figure 3 Simulated amplification spectrum for a 5 mm YCOB crystal pumped at 515 nm with an intensity of ~50 GW/cm2.
Figure 4 Simulated noncollinear angular dependence of the BiBO amplified spectrum. Crystal thickness is 2.5 mm and the pump intensity is ~50 GW/cm2.
Figure 5 Schematic of the OPCPA chain used for crystal comparison. SHG, second harmonic generation; WLG, white light generation.
Figure 6 Noncollinear OPA stage seed: supercontinuum generation.
Figure 7 Experimental results for the YCOB NOPA stage compared to theoretical analysis. Amplified spectra for (a) 5 mm, (b) 7.5 mm and (c) 15 mm crystals. The shadowed curve is the numerically calculated amplified spectrum for the following parameters: λ p = 515 nm, I p ~50 GW/cm2, d eff = 5, 7.5, 15 mm YCOB crystal thicknesses, and the signal and crystal angles are those reported in Table 2.
4 Results
An extraction beam optical path was set at the output of the sapphire crystal to measure the spectral bandwidth of the supercontinuum (WLG). The measured WLG spectrum of the beam, acting as an ultra-short broadband seed of the designed noncollinear OPA stage, is shown in Figure 6.
Figure 8 Experimental results for the BiBO NOPA stage: amplified spectrum for a 2.5 mm crystal. Different noncollinear angles are plotted to show the influence of θ NC on the spectral dip around 920 nm.
Figure 9 Theoretical amplified spectrum for LBO and BBO crystals in a noncollinear geometry to maximize the bandwidth.
The fringes observed in the measured spectrum could be linked to multiple filament generation, leading to an unstable spectral phase. To mitigate this effect, we implemented a soft aperture on the beam to ensure an ideal trade-off between the single filament and broadband operation. The fringed spectral phase would be worrisome for pulse compression. It should be noted, however, that these features are due to the seed signal used and not due to the amplification process.
4.1 YCOB NOPA performance
The 5 mm YCOB crystal was pumped at 515 nm with an intensity of ~50 GW/cm2. A 200 nm amplified bandwidth (1/e 2 width) is observed, ranging from 780 nm to 980 nm (Figure 7(a)).
We have performed measurements with the seed beam blocked, and no gain was observed. Ten consecutive shots are plotted to show the NOPA stability in terms of bandwidth. The visible shot-to-shot fluctuations are a result of the nonlinear supercontinuum generation process (namely, multi-filament operations and unstable spectral phase) and are not affecting the amplified bandwidth.
The results from the simulated data (shaded curve) agree well with the measured experimental spectra.
In order to study the influence of the crystal thickness on the amplified bandwidth and the gain, in Figures 7(b) and 7(c) we present the experimental results with the 7.5 mm and 15 mm crystals, for the same pump power and phase-matching angles. As expected, a bandwidth-narrowing effect is observed as the crystal thickness L C increases, since, for a constant phase mismatch, gain only occurs while ∆k(λ) × L < π/2. A small decrease of about 10 nm in the bandwidth was observed when employing the 7.5 mm crystal in the shorter wavelength region of the spectrum, while with the 15 mm crystal gain narrowing occurs on both sides of the spectrum. Adopting a pump power of ~50 GW/cm2, an experimental gain of ~2 × 102 is maintained for the three sets of data, confirming a strong saturation regime. From the simulation, the corresponding calculated small-signal gain is ~3 × 102 for the 5 mm YCOB crystal, in good agreement with the experimental data. Also for this case, the gain is distributed over the entire bandwidth and is approximately homogeneous, while increasing the crystal length leads to a peaked spectrum, around 850 nm for the 15 mm crystal.
4.2 BiBO NOPA performance
In this case only one crystal length was available, so the performance was optimized by slightly readjusting the noncollinear angle obtained from the simulations (Table 2) and the focusing distance. The 2.5 mm BiBO crystal was pumped at 515 nm with an intensity of ~50 GW/cm2. A 240 nm amplified bandwidth (1/e 2 width) is obtained, ranging from 810 nm to 1050 nm as shown in Figure 8. Measurements were carried out after blocking the seed, and no gain was observed. The simulated data is in excellent agreement with the measured experimental spectra. As before, ten consecutive shots are plotted to show the NOPA stability, with the shot-to-shot fluctuations resulting from the nonlinear supercontinuum generation process. The OPA process is more efficient for the BiBO stage than for the YCOB one, noticeably thanks to the reported higher gain. Additionally, from the simulation prediction we may infer to be closer to the saturation regime (with respect to YCOB). This is experimentally supported by the above-mentioned higher gain and the smoother fluctuations observed (cf. Figure 7 vs. Figure 8).
There is a noticeable soft cut-off in the longer wavelength region of the amplified spectrum resulting from the 1030 nm filter mentioned in Section 3. A noncollinear angle scan was performed experimentally but differences in the amplified spectrum were not appreciable, as opposed to the theoretical scan. The pump power adopted (~50 GW/cm2) results in an experimental gain of ~8 × 102, in good agreement with the calculated small-signal gain of ~7 × 102.
5 Result comments
By comparing the performance of the two crystals at similar pump intensities (~50 GW/cm2) in this low-energy regime, a number of conclusions can be drawn.
• Yttrium calcium oxyborate shows a gain considerably smaller than BiBO, even for a crystal twice as long (5 mm vs. 2.5 mm).
• Bismuth borate enables an ultra-broadband amplification spectrum, about 40 nm wider than with YCOB.
• As predicted by theory regarding the crystal properties, the YCOB amplified spectrum (as in the widely used LBO[Reference Galletti, Oliveira and Galimberti42] crystals, shown in Figure 9) is more homogeneous in respect to the BiBO one, which presents a dip centered in the spectrum, like the widely used BBO crystal (usually adopted with gain centered at 800 nm), shown in Figure 9.
From this we can infer that BiBO can play a major role in OPA in the low-energy, few-cycle regime because of the broadband, high gain capability presented. One simple way to remove the spectral dip and lead to a more homogeneous spectrum is through the implementation of a second NOPA stage with a different noncollinear angle, in order to shift the amplified spectral region. Concerning YCOB, and based on the recently demonstrated large aperture growth capability, the high nonlinear coefficient
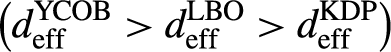$$\left({d}_{\mathrm{eff}}^{\mathrm{YCOB}}>{d}_{\mathrm{eff}}^{\mathrm{LBO}}>{d}_{\mathrm{eff}}^{\mathrm{KDP}}\right)$$
and the broadband flat spectrum supported, it can efficiently replace the more common crystals (such as LBO and DKDP) used in the high-energy, few-cycle regime.
In order to place these results in a wider context and understand their relevance better, we performed similar simulations for the supported bandwidth of BBO and LBO stages, comparing their outputs with the significant experimental results present in the literature. Figure 9 shows the calculated amplified spectrum (centered at ~870 nm) for a 5 mm thick LBO crystal (d eff ~1) and a 2.5 mm thick BBO crystal (d eff ~1.9), pumped at 515 nm with an intensity of ~50 GW/cm2 with the respective noncollinear angle optimized for operation in the ultra-broadband regime. While from these simulations an ultra-broad bandwidth (~300 nm, 1/e 2 width) would be expected, experimental results for the amplified spectrum have been more modest, as mentioned in Section 1.
We conclude that the BiBO nonlinear crystal shows a great potential to replace the commonly used BBO thanks to its broader supported bandwidth (Figure 8 vs. Figure 9) and higher d eff (Table 2), leading to higher gain; and, at the same time, YCOB is a valuable alternative to LBO (both in low- and high-energy systems), maintaining the same capability for being grown thickly, ultra-broadband operation (Figure 7(a) vs. Figure 9), but showing a higher d eff (Table 2) corresponding to higher gain. Finally, because both present a higher d eff with respect to their more common alternatives, they allow the adoption of thinner crystals to reach the same overall gain, while leading to the minimization of the spatial walk-off effect, which is important for preventing the deterioration of the amplification process.
6 Conclusions
The experimental results presented, benchmarked with simulations, show that YCOB and BiBO are able to support ultra-broad bandwidth, high gain operation, with comparable (in the case of YCOB) or even better (in the case of BiBO) results in comparison with the commonly used nonlinear crystals. We also showed that BiBO is a perfect candidate for low-energy OPA stages, surpassing BBO/LBO in both conversion efficiency and supported bandwidth (reaching up to 240 nm). Bismuth borate presents a higher gain although a less homogeneously amplified spectrum. For the high-energy stages, YCOB is a good candidate with its capability of being grown as large as LBO and KDP, and its large supported bandwidth, while maintaining a high gain. Yttrium calcium oxyborate, in fact, can even be used for low-energy stages where it has similar performance to LBO (surpassed only by BBO and BiBO), but is best suited for high-energy stages such as those to be implemented in future multi-petawatt systems, where it allows ultra-short pulses to be scaled to high energies.
In summary, we have described the broadband operation of these two nonlinear crystals and evaluated their performance. They can be implemented in low- or high-energy NOPA stages, competing or surpassing the performance of the more well-known BBO and LBO. We expect these results to be useful for the community of high-power laser developers at large.
Acknowledgments
This project was financially supported by the European Union’s Horizon 2020 research and innovation program under grant agreement No. 871124 (Laserlab-Europe), the Euratom research and training program 2014–2018 under grant agreement No. 633053 and the Fundação para a Ciencia e a Tecnologia (FCT, Lisboa) under grants Nos. PD/BD/114327/2016, PD/BD/135177/2017, PD/BD/135222/2017 and PINFRA/22124/2016; it was carried out in the framework of the Advanced Program in Plasma Science and Engineering (APPLAuSE, sponsored by FCT under grant No. PD/00505/2012) at Instituto Superior Técnico (IST).
Open access
