1 Introduction
Turbulence is a phenomenon that pervades most liquid, gas, and plasma flows in engineering and nature, ranging from high-speed engines, nuclear fusion power reactors to star formation in molecular clouds[Reference Audit and Hennebelle1], and supernovae[Reference Röpke, Hillebrandt, Schmidt, Niemeyer, Blinnikov and Mazzali2]. Seventy years have passed since Kolmogorov formulated his successful theory of incompressible turbulence, yet one observes a stark absence of an analogous framework to describe high-speed flows with significant compressibility effects, such as in the aforementioned systems. An exact Kolmogorov-like scaling law for compressible turbulence (based on the density-weighted fluid velocity) has just been demonstrated very recently[Reference Galtier and Banerjee3]. A key remaining unsolved question is the transition of a flow to a turbulent state and over what time span does this transition occur. The transition to turbulence in a high density and compressible medium is probably the least understood problem in high energy density matter, either theoretically or experimentally. Novel laser facilities, such as the National Ignition Facility (NIF) and the Laser Megajoule (LMJ), are unique energy drivers which allow creating high Reynolds and high Mach numbers flows in the laboratory and measuring for the first time the transition to turbulence in hot dense plasmas.
High energy density physics (HEDP)[Reference Drake4] in the laboratory is a field that emerged in the last two decades[Reference Remington, Arnett, Drake and Takabe5] thanks to the development of high power laser facilities. The high energy density regime refers to energy densities exceeding
![]() $10^{11}$
joules per cubic meter
$10^{11}$
joules per cubic meter
![]() $(E/V>10^{11}~\text{J}/\text{m}^{3})$
, which cannot be achieved in static laboratory experiments. One of the most relevant HEDP areas is laboratory astrophysics[Reference Remington, Drake and Ryutov6]. High power laser facilities are already being used to perform experiments in a parameter range where scaling relations could be applied to extrapolate the results of plasma physics studies to astrophysical conditions[Reference Falize, Michaut and Bouquet7].
$(E/V>10^{11}~\text{J}/\text{m}^{3})$
, which cannot be achieved in static laboratory experiments. One of the most relevant HEDP areas is laboratory astrophysics[Reference Remington, Drake and Ryutov6]. High power laser facilities are already being used to perform experiments in a parameter range where scaling relations could be applied to extrapolate the results of plasma physics studies to astrophysical conditions[Reference Falize, Michaut and Bouquet7].
While the issue of hydrodynamic instabilities has been identified since the beginning of the field of HED laboratory astrophysics, and scaled laser experiments performed (see Ref. [Reference Remington, Drake and Ryutov6] for a review), turbulent HED plasma flows were just approached very recently[Reference Smalyuk, Hansen, Hurricane, Langstaff, Martinez, Park, Raman, Remington, Robey, Schilling, Wallace, Elbaz, Shimony, Shvarts, Di Stefano, Drake, Marion, Kraul and Kuranz8]. This is mainly due to a lack of laser energy to sustain HED flows for a sufficiently long time to transition to a turbulent stage[Reference Casner, Smalyuk, Masse, Moore, Delorme, Martinez, Igumenshchev, Jacquet, Liberatore, Seugling, Chicanne, Park and Remington9, Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10]. The next generation of HED laboratory plasma experiments to be performed on the NIF[Reference Moses, Boyd, Remington, Keane and Al-Ayat11] and LMJ–PETAL[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel12, 13] places us at the frontier of a new regime in physics. Megajoule (MJ) scale lasers open up novel areas of research and also push existing areas into qualitatively new regimes either identical or similar to the astrophysical ones.
We propose to bridge the gap between the compressible turbulence and HED plasmas by performing laser plasma experiments in these unexplored regimes. The challenge is to isolate specific processes that satisfy a scaling relation between the laboratory and astrophysics and to use experimental data to validate the physical models identified in the simulations. We will in particular focus on supernova remnants (SNRs) because understanding their morphological evolution is important to assess both explosion models of supernovae, of which SNRs are fingerprints and large scale models of the turbulent interstellar medium (ISM), for which SNRs are seeds. It has long been argued that SNRs would be subject to fluid instabilities[Reference Schmidt and Federrath14, Reference Arnett15]. The question is whether these fluid instabilities alone are sufficient to explain the observed morphology.

Figure 1. Schematics of the tasks of the TurboHEDP project with their interactions.
We follow an analytical and step-by-step approach and concentrate first in a planar geometry on one of the canonical hydrodynamic instabilities leading to turbulence[Reference Chandrasekhar16]: the Rayleigh–Taylor instability (RTI) prevalent when a heavy fluid is supported by a lighter one. The Kelvin–Helmholtz instability (KHI), which arises from adjacent fluids streaming at different velocities, could also be studied as a side effect of the RTI at the highly nonlinear stage. In HED flows these instabilities are complicated by strong shock waves, steep density gradients, nonideal equation of states and nonlocal energy transport by particles and radiation. Until now, few laboratory experiments have explored the combined effect of instability growth and radiative effects[Reference Edens, Adams, Rambo, Ruggles, Smith, Porter and Ditmire17]. An outstanding uncertainty is whether the properties of materials at HED conditions will modify the understanding developed from non-HED experiments.
The TurboHEDP project aims to tackle the following questions.
— How to create compressible hydrodynamic instabilities in laser plasma experiments relevant for our understanding of astrophysical phenomena?
— How to measure the development of these instabilities in their turbulent stage with enhanced spatial and temporal resolution?
— How to simulate these HED experiments accurately and leverage the results to improve astrophysical codes?
Our goals are therefore to study the physics of turbulent flows in HED plasmas, to develop the appropriate numerical tools and to prepare future experiments on larger scale facilities through experimental campaigns performed at subscale laser energies. This will allow us to create both experimental and numerical platforms with predictive capabilities, and to leverage the results to improve astrophysical simulations. The interplay between experiments and simulations, at the core of our research project, is schematized in Figure 1. The paper is organized as the following. In Section 2, a reminder about the physics of young supernova remnant explosion is given and we review the state of the art of nonlinear hydrodynamics experiments in HED plasma. Then we draw the envisioned roadmap of our experiments. In Section 3, novel experimental results acquired for RTI experiments in deceleration on the LULI2000 facility are presented. These data define the baseline for future LMJ–PETAL experiments, whose design is presented in Section 4 Conclusion and perspectives are given in Section 5.
2 State of the art of laser-driven hydrodynamics experiments relevant for laboratory astrophysics
2.1 Astrophysical applications
Among the many astrophysical situations where Rayleigh–Taylor and Kelvin–Helmholtz instabilities occur, let us consider first simple cases with pure hydrodynamic flows and without complications related to radiation transfer or losses. One such particular example is a young supernova remnant of an age of a few hundred years, developing in a uniform interstellar medium. The cold ejecta expands with a homologous density profile
![]() $\unicode[STIX]{x1D70C}(v)$
falling down steeply (as a power law or an exponential) in the outer layers that first meet the ambient gas. This leads to a double shock structure (the main blast wave propagating into the ambient gas and the reverse shock into the ejecta) resulting in an expanding shell of hot gas. The pressure increases outwards in the hot gas (the gas decelerates), while density decreases outwards inside the shocked ejecta[Reference Ferrand, Decourchelle, Ballet and Teyssier18, Reference Fraschetti, Teyssier, Ballet and Decourchelle19]. These opposite pressure and density gradients lead naturally to RTI, as qualitatively observed in Chandra X-rays images of the famous Tycho (SN 1572) SNR.
$\unicode[STIX]{x1D70C}(v)$
falling down steeply (as a power law or an exponential) in the outer layers that first meet the ambient gas. This leads to a double shock structure (the main blast wave propagating into the ambient gas and the reverse shock into the ejecta) resulting in an expanding shell of hot gas. The pressure increases outwards in the hot gas (the gas decelerates), while density decreases outwards inside the shocked ejecta[Reference Ferrand, Decourchelle, Ballet and Teyssier18, Reference Fraschetti, Teyssier, Ballet and Decourchelle19]. These opposite pressure and density gradients lead naturally to RTI, as qualitatively observed in Chandra X-rays images of the famous Tycho (SN 1572) SNR.
One of the main results of those morphological observations is the measure of the shell width of the shocked ambient gas. This width is inversely proportional to the compression at the shock, which is equal to 4 (corresponding to the polytropic index
![]() $\unicode[STIX]{x1D6FE}=5/3$
) for a strong shock in ionized gas. However cosmic-ray acceleration at the shock front leads to stronger compression. In other words the width of the shell is a measure of how much energy goes into the cosmic rays in the shock. This observable is however impeded by the RTI which makes it impossible to locate precisely the contact discontinuity. It is therefore necessary to rely on simulations[Reference Ferrand, Decourchelle, Ballet and Teyssier18] to estimate the extent of the RTI fingers and convert the measurement (how close the ejecta gets to the shock) into the desirable parameters. These simulations at the astrophysics scale can be compared to the results of a laser-initiated flow to check that they reproduce the controlled experiment, enhancing confidence in the underlying physical models.
$\unicode[STIX]{x1D6FE}=5/3$
) for a strong shock in ionized gas. However cosmic-ray acceleration at the shock front leads to stronger compression. In other words the width of the shell is a measure of how much energy goes into the cosmic rays in the shock. This observable is however impeded by the RTI which makes it impossible to locate precisely the contact discontinuity. It is therefore necessary to rely on simulations[Reference Ferrand, Decourchelle, Ballet and Teyssier18] to estimate the extent of the RTI fingers and convert the measurement (how close the ejecta gets to the shock) into the desirable parameters. These simulations at the astrophysics scale can be compared to the results of a laser-initiated flow to check that they reproduce the controlled experiment, enhancing confidence in the underlying physical models.
In a young SNR the flow is diverging (3D dilution) so the acceleration that drives the RTI is decreasing with time. For a power-law density profile in the ejecta the evolution is self-similar and (after a brief period of initial growth) the extent of the RT fingers remains a fixed fraction of the radius[Reference Fraschetti, Teyssier, Ballet and Decourchelle19]. This situation can be modeled in an experiment with an equivalent Atwood number
![]() $A=(\unicode[STIX]{x1D70C}_{1}-\unicode[STIX]{x1D70C}_{2})/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})$
that can be fitted in a simulation. Therefore, based on astrophysical observations and the state of the art of 3D simulations, we can define a scaled laser experiment. The measurement of the extending of the RTI mixing zone for various initial conditions (2D versus 3D initial pattern) will be used to benchmark the astrophysical simulations, enabling eventually a progress in the understanding of back-reaction of particles on the SNR evolution[Reference Ferrand, Decourchelle, Ballet and Teyssier18, Reference Warren, Hughes, Badenes, Ghavamiam, McKee, Moffett, Plucinsky, Rakowski, Reynoso and Slane20].
$A=(\unicode[STIX]{x1D70C}_{1}-\unicode[STIX]{x1D70C}_{2})/(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})$
that can be fitted in a simulation. Therefore, based on astrophysical observations and the state of the art of 3D simulations, we can define a scaled laser experiment. The measurement of the extending of the RTI mixing zone for various initial conditions (2D versus 3D initial pattern) will be used to benchmark the astrophysical simulations, enabling eventually a progress in the understanding of back-reaction of particles on the SNR evolution[Reference Ferrand, Decourchelle, Ballet and Teyssier18, Reference Warren, Hughes, Badenes, Ghavamiam, McKee, Moffett, Plucinsky, Rakowski, Reynoso and Slane20].
2.2 State of the art of nonlinear hydrodynamics HED experiments and TurboHEDP experimental roadmap
2.2.1 Advances in nonlinear hydrodynamics HED experiments relevant for laboratory astrophysics
Supernovae (SN) are transient astronomical events with spectacular brightness which originate from the explosion of a massive star at the end of its life. Gravitational SN explosion occurs when the core suffers a gravitational collapse that sends a shock wave through the surrounding shells of the extinguishing star. This phenomenon is a beautiful example of singularity in compressible fluid mechanics[Reference Pomeau, Le Berre, Chavanis and Denet21]. The most famous and observed SN is probably SN1987A, which has been the first one to be detected and followed by science in the modern days. Until now, existing models fail to explain the degree of mixing and the observed outward velocities of material ejected from deep layers in the star[Reference Kifonidis, Plewa, Scheck, Janka and Müller22]. These inconsistencies gave birth to numerous laser astrophysics experiments relevant for SN[Reference Remington, Drake and Ryutov6, Reference Kuranz, Drake, Grosskopf, Fryxell, Budde, Hansen, Miles, Plewa, Hearn and Knauer23]. Despite a certain level of nonlinearity, the loss of memory of initial conditions (one of the criteria of a turbulent flow) does not happen in these experiments. Limitations are primary due to the lack of sufficient laser energy to sustain steady shock conditions long time enough to enter the highly nonlinear stage of the RTI[Reference Casner, Smalyuk, Masse, Moore, Delorme, Martinez, Igumenshchev, Jacquet, Liberatore, Seugling, Chicanne, Park and Remington9, Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10].
The morphological structure of SNRs is the key link between stars and ISM. Being fingerprints of SN explosions, SNRs are so energetic that their outflows provide a mechanism of turbulence injection in the ISM[Reference Ryan Joung, Mac Low and Bryan24]. A supersonic turbulence is prevailing at all scales within ISM and determines the star formation rate in molecular clouds[Reference Mac Low and Klessen25]. The ISM turbulence is nevertheless magnetized and magnetohydrodynamic (MHD) flows are out of scope of this project. However shear driven flows are also candidates for turbulence injection and magnetization in the ISM[Reference Miniati26]. Jets propagating through the interstellar medium are also potentially susceptible to drive instabilities, such as the shear Kelvin–Helmholtz and RT instabilities[Reference Matsumoto and Masada27]. The prototype of a shear driven flow is in fact the KHI which occurs when a velocity shear difference exists at an interface between two fluids. The KHI is the natural companion of the RTI. At the nonlinear stage of RTI, while denser spikes penetrate through a low-density material, small perturbations at the spike surface can grow due to the KHI, resulting in mushroom-like structures as partially visible in Ref. [Reference Kuranz, Drake, Grosskopf, Fryxell, Budde, Hansen, Miles, Plewa, Hearn and Knauer23]. In contrary to classical fluid and gas experiments, the first measurements of KHI in HEDP were only performed recently[Reference Smalyuk, Hansen, Hurricane, Langstaff, Martinez, Park, Raman, Remington, Robey, Schilling, Wallace, Elbaz, Shimony, Shvarts, Di Stefano, Drake, Marion, Kraul and Kuranz8].
When looking at the experimental radiographs in Refs. [Reference Smalyuk, Hansen, Hurricane, Langstaff, Martinez, Park, Raman, Remington, Robey, Schilling, Wallace, Elbaz, Shimony, Shvarts, Di Stefano, Drake, Marion, Kraul and Kuranz8, Reference Kuranz, Drake, Grosskopf, Fryxell, Budde, Hansen, Miles, Plewa, Hearn and Knauer23], one could say that a turbulent HED stage has not yet been reached. Schematically, turbulence requires very high Reynolds numbers in excess of
![]() $10^{5}$
. A minimum turbulent state has been defined by Zhou with
$10^{5}$
. A minimum turbulent state has been defined by Zhou with
![]() $Re_{m}=1.5\times 10^{5}$
[Reference Zhou28]. The Reynolds number
$Re_{m}=1.5\times 10^{5}$
[Reference Zhou28]. The Reynolds number
![]() $Re$
is defined as the ratio
$Re$
is defined as the ratio
![]() $Re=UL/\unicode[STIX]{x1D708}$
where
$Re=UL/\unicode[STIX]{x1D708}$
where
![]() $U$
is the typical fluid velocity,
$U$
is the typical fluid velocity,
![]() $L$
the characteristic size of the experiment and
$L$
the characteristic size of the experiment and
![]() $\unicode[STIX]{x1D708}$
the kinematic viscosity. Increasing
$\unicode[STIX]{x1D708}$
the kinematic viscosity. Increasing
![]() $Re$
in laser experiments means driving a larger sample at a higher velocity, which translates into the necessity of greater laser energy. Increasing the lateral dimension
$Re$
in laser experiments means driving a larger sample at a higher velocity, which translates into the necessity of greater laser energy. Increasing the lateral dimension
![]() $L$
of the target allows also avoiding boundary effects. In fact, rarefaction waves propagating back from the lateral sides are detrimental and perturb either the measurements and/or the interpretation.
$L$
of the target allows also avoiding boundary effects. In fact, rarefaction waves propagating back from the lateral sides are detrimental and perturb either the measurements and/or the interpretation.
That is the reason why MJ class laser facilities such as LMJ–PETAL[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel12, 29] and NIF[Reference Moses, Boyd, Remington, Keane and Al-Ayat11] are real game-changers in the field of HED hydrodynamics. They allow accelerating a larger sample over a longer time period than previously achieved. Not only the laser energy is important but also the time duration of the laser pulse, which defines the acceleration time. For the RTI-driven turbulence, the transition to turbulence depends on merging of bubbles. Initial perturbations of the interface develop into a mixing zone made of the rising bubbles of a light fluid interleaved with falling spikes of a heavy fluid (see Figure 2(a) at ablation front as an illustrating example). When the initial perturbation is multimode, the flow is governed by a bubble-competition, bubble-merger regime with larger bubbles overtaking smaller ones[Reference Oron, Alon and Shvarts30]. After 2–3 merging generations a self-similar regime is reached where the RTI bubble front
![]() $h_{b}$
evolves as
$h_{b}$
evolves as
![]() $h_{b}=\unicode[STIX]{x1D6FC}_{b}Agt^{2}$
[Reference Dimonte, Ramaprabhu, Youngs, Andrews and Rosner31]. Longer acceleration time leads therefore to more bubbles merging and a larger mixing zone[Reference Malamud, Grosskopf and Drake32]. The same analysis based on 2D statistical models leads also to self-similar evolution laws for Richtmyer–Meshkov instability (RMI) and KHI mixing zones[Reference Rikanati, Oron, Alon and Shvarts33, Reference Zhou34]. A general question for all of these instabilities is what determines the late-time asymptotic structure of the mixing region. For RTI, what are the value and the dependence of the parameter
$h_{b}=\unicode[STIX]{x1D6FC}_{b}Agt^{2}$
[Reference Dimonte, Ramaprabhu, Youngs, Andrews and Rosner31]. Longer acceleration time leads therefore to more bubbles merging and a larger mixing zone[Reference Malamud, Grosskopf and Drake32]. The same analysis based on 2D statistical models leads also to self-similar evolution laws for Richtmyer–Meshkov instability (RMI) and KHI mixing zones[Reference Rikanati, Oron, Alon and Shvarts33, Reference Zhou34]. A general question for all of these instabilities is what determines the late-time asymptotic structure of the mixing region. For RTI, what are the value and the dependence of the parameter
![]() $\unicode[STIX]{x1D6FC}_{b}$
on the initial conditions[Reference Dimonte, Ramaprabhu, Youngs, Andrews and Rosner31, Reference Zhou34]? This question remains open and has not yet been addressed in HED plasmas, whereas
$\unicode[STIX]{x1D6FC}_{b}$
on the initial conditions[Reference Dimonte, Ramaprabhu, Youngs, Andrews and Rosner31, Reference Zhou34]? This question remains open and has not yet been addressed in HED plasmas, whereas
![]() $\unicode[STIX]{x1D6FC}_{b}$
is a key subgrid parameter in SN simulations[Reference Arnett15, Reference Hicks and Rosner35].
$\unicode[STIX]{x1D6FC}_{b}$
is a key subgrid parameter in SN simulations[Reference Arnett15, Reference Hicks and Rosner35].

Figure 2. (a) FCI2 calculations showing bubble-merger regime for indirect-drive experiments on NIF[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Dimonte, Ramaprabhu, Youngs, Andrews and Rosner31, Reference Malamud, Grosskopf and Drake32]. (b) Experimental configuration with simultaneous face-on and side-on radiographies. (c) Face-on radiograph acquired at
![]() $t=18.7~\text{ns}$
. (d) The lineout extracted from (c) shows how the initial broadband pattern (in red) has evolved into 6 main bubbles as a result of the bubble-competition regime.
$t=18.7~\text{ns}$
. (d) The lineout extracted from (c) shows how the initial broadband pattern (in red) has evolved into 6 main bubbles as a result of the bubble-competition regime.

Figure 3. Envisioned laser plasma experiments within the TurboHEDP project. The higher the laser energy and the longer the laser drive, the more nonlinear HED flows become, with the final goal to create on LMJ turbulent HED flows. Typical side-on views of ablative RTI single-mode and multi-mode simulations[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36] are shown to illustrate the increasing level of nonlinearity of the flows expected on each facility.
A striking demonstration of the experimental capabilities enabled by a MJ laser facility is shown in Figure 2. The Discovery Science Ablative RTI proposal on NIF was devoted from 2013 to 2015 to the study of the highly nonlinear stage of the ablative RTI[Reference Casner, Smalyuk, Masse, Moore, Delorme, Martinez, Igumenshchev, Jacquet, Liberatore, Seugling, Chicanne, Park and Remington9, Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10]. Thanks to a 20-ns-shaped laser pulse and
![]() ${\sim}$
266 kJ of laser energy, a bubble-merger regime for RTI at ablation front has been evidenced for the first time in indirect drive starting from a 2D broadband pre-imposed modulation[Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38]. The experimental configuration is shown in Figure 2(b). A major advantage of multibeam laser facilities is the capability to perform simultaneous radiographies along different lines of sight. Figure 2(c) displays a typical NIF face-on X-ray radiograph acquired at late time. The consecutive black and white vertical lines correspond to 2D RTI bubbles and spikes. Lineouts across the image evidence the bubble-merger regime. Starting from the initial pattern shown in red in Figure 5(d), 50 initial bubbles have merged, leading to 6 principal bubbles at 18.7 ns[Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38]. These results were obtained within a minimum number of shots (6), demonstrating the ability of large scale facilities to deliver reproducible drive conditions.
${\sim}$
266 kJ of laser energy, a bubble-merger regime for RTI at ablation front has been evidenced for the first time in indirect drive starting from a 2D broadband pre-imposed modulation[Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38]. The experimental configuration is shown in Figure 2(b). A major advantage of multibeam laser facilities is the capability to perform simultaneous radiographies along different lines of sight. Figure 2(c) displays a typical NIF face-on X-ray radiograph acquired at late time. The consecutive black and white vertical lines correspond to 2D RTI bubbles and spikes. Lineouts across the image evidence the bubble-merger regime. Starting from the initial pattern shown in red in Figure 5(d), 50 initial bubbles have merged, leading to 6 principal bubbles at 18.7 ns[Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38]. These results were obtained within a minimum number of shots (6), demonstrating the ability of large scale facilities to deliver reproducible drive conditions.
The work described in details thereafter builds on these recent experimental successes, with the ambition to take us to a qualitatively new level of what we can do in terms of scaled laboratory astrophysics experiments. Reaching a turbulent regime for RTI at a classical interface requires accelerating samples over timescales of tens to a hundred nanoseconds of drive, with velocities of a few tens
![]() $\unicode[STIX]{x03BC}\text{m}\cdot \text{ns}^{-1}$
and sample lateral size of a few millimeters to avoid the detrimental effects of lateral rarefaction waves. Accelerating samples over such a long time with X-ray drive (even with the recently developed multi-barrel hohlraum concept[Reference Casner, Martinez, Smalyuk, Masse, Kane, Villette, Fariaut, Oudot, Liberatore, Mancini, Remington and Heeter39, Reference Kane, Martinez, Pound, Heeter, Casner and Mancini40]) without stagnation effects seems difficult. Direct-drive (DD) experiments are the right solution and constitute the heart of the TurboHEDP project. DD physics can moreover be simulated with academic radiative hydrocodes, such as CHIC[Reference Breil, Galera and Maire41] and FLASH[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb42]. The development of a predictive numerical platform for DD experiments on LMJ–PETAL is synergetic with the recent commissioning of a long-pulse DD platform on NIF[Reference Casner, Mailliet, Khan, Martinez, Izumi, Kalantar, Di Nicola, Di Nicola, Le Bel, Igumenshchev, Tikhonchuk, Remington, Masse and Smalyuk43].
$\unicode[STIX]{x03BC}\text{m}\cdot \text{ns}^{-1}$
and sample lateral size of a few millimeters to avoid the detrimental effects of lateral rarefaction waves. Accelerating samples over such a long time with X-ray drive (even with the recently developed multi-barrel hohlraum concept[Reference Casner, Martinez, Smalyuk, Masse, Kane, Villette, Fariaut, Oudot, Liberatore, Mancini, Remington and Heeter39, Reference Kane, Martinez, Pound, Heeter, Casner and Mancini40]) without stagnation effects seems difficult. Direct-drive (DD) experiments are the right solution and constitute the heart of the TurboHEDP project. DD physics can moreover be simulated with academic radiative hydrocodes, such as CHIC[Reference Breil, Galera and Maire41] and FLASH[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb42]. The development of a predictive numerical platform for DD experiments on LMJ–PETAL is synergetic with the recent commissioning of a long-pulse DD platform on NIF[Reference Casner, Mailliet, Khan, Martinez, Izumi, Kalantar, Di Nicola, Di Nicola, Le Bel, Igumenshchev, Tikhonchuk, Remington, Masse and Smalyuk43].
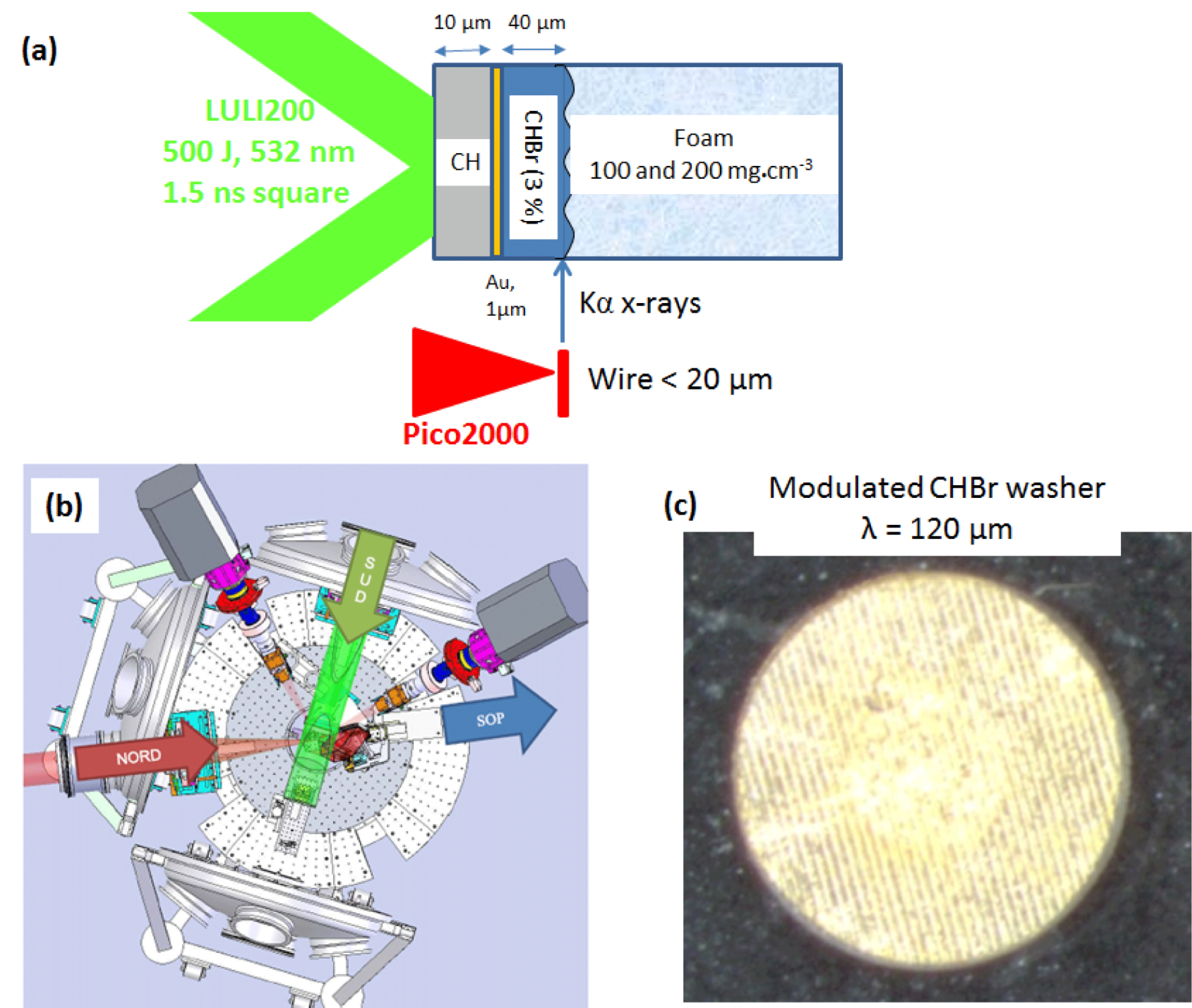
Figure 4. (a) Schematic of the targets design for a bottom-up X-ray radiograph using Pico2000 laser beam. (b) Target chamber layout. (c) Example of a fabricated modulated package produced at Scitech. The pre-imposed ripples are visible in the central part of the package.

Figure 5. Experimental radiographs acquired on imaging plate (IP) on LULI2000. Acquisition times correspond to the Pico2000 delay relative to the main drive. The first RTI data were acquired on Shot 22 and Shot 23.
As well as our understanding of cosmos has improved with the development of space-based X-ray observatories, we should gain in precision in laser plasma experiments with the development of transformative X-ray diagnostics. X-ray radiography is indeed the workhorse of HED hydrodynamics experiments. The need of a large (0.5 mm) field of view 2D X-ray imager with the spatial resolution
![]() ${<}10~\unicode[STIX]{x03BC}\text{m}$
has been identified on large scale laser facilities. These capabilities could be achieved with grazing angle-of-incidence mirrors imaging systems like Kirkpatrick–Baez microscopes[Reference Pickworth, Ayers, Bell, Brejnholt, Buscho, Bradley, Decker, Hau-Riege, Kilkenny, McCarville, Pardini, Vogel and Walton44–Reference Rosch, Rosch, Trosseille, Caillaud, Allouche, Bourgade, Briat, Brunel, Burillo, Casner, Depierreux, Gontier, Jadaud, Le Breton, Llavador, Loupias, Miquel, Oudot, Perez, Raimbourg, Rousseau, Rousseaux, Rubbelynck, Stemmler, Troussel, Ulmer, Wrobel, Beauvais, Pallet and Prevot46], which offer the best solution in terms of resolution versus signal to noise ratio. The X-ray imagers of the LIL facility were all based on the Kirkpatrick–Baez microscope[Reference Rosch, Boutin, Le Breton, Gontier, Jadaud, Reverdin, Lidove and Maroni45] and the first LMJ imager operational in 2014 also works with grazing incidence mirrors[Reference Rosch, Rosch, Trosseille, Caillaud, Allouche, Bourgade, Briat, Brunel, Burillo, Casner, Depierreux, Gontier, Jadaud, Le Breton, Llavador, Loupias, Miquel, Oudot, Perez, Raimbourg, Rousseau, Rousseaux, Rubbelynck, Stemmler, Troussel, Ulmer, Wrobel, Beauvais, Pallet and Prevot46]. A high-resolution X-ray imaging diagnostic is operational on the NIF[Reference Pickworth, Ayers, Bell, Brejnholt, Buscho, Bradley, Decker, Hau-Riege, Kilkenny, McCarville, Pardini, Vogel and Walton44], and under development on LMJ[Reference Troussel, Dennetiere, Maroni, Hoghoj, Hedacq, Cibik and Krumrey47]. In the following, we will present a novel diagnostic, based on lithium fluoride detectors.
${<}10~\unicode[STIX]{x03BC}\text{m}$
has been identified on large scale laser facilities. These capabilities could be achieved with grazing angle-of-incidence mirrors imaging systems like Kirkpatrick–Baez microscopes[Reference Pickworth, Ayers, Bell, Brejnholt, Buscho, Bradley, Decker, Hau-Riege, Kilkenny, McCarville, Pardini, Vogel and Walton44–Reference Rosch, Rosch, Trosseille, Caillaud, Allouche, Bourgade, Briat, Brunel, Burillo, Casner, Depierreux, Gontier, Jadaud, Le Breton, Llavador, Loupias, Miquel, Oudot, Perez, Raimbourg, Rousseau, Rousseaux, Rubbelynck, Stemmler, Troussel, Ulmer, Wrobel, Beauvais, Pallet and Prevot46], which offer the best solution in terms of resolution versus signal to noise ratio. The X-ray imagers of the LIL facility were all based on the Kirkpatrick–Baez microscope[Reference Rosch, Boutin, Le Breton, Gontier, Jadaud, Reverdin, Lidove and Maroni45] and the first LMJ imager operational in 2014 also works with grazing incidence mirrors[Reference Rosch, Rosch, Trosseille, Caillaud, Allouche, Bourgade, Briat, Brunel, Burillo, Casner, Depierreux, Gontier, Jadaud, Le Breton, Llavador, Loupias, Miquel, Oudot, Perez, Raimbourg, Rousseau, Rousseaux, Rubbelynck, Stemmler, Troussel, Ulmer, Wrobel, Beauvais, Pallet and Prevot46]. A high-resolution X-ray imaging diagnostic is operational on the NIF[Reference Pickworth, Ayers, Bell, Brejnholt, Buscho, Bradley, Decker, Hau-Riege, Kilkenny, McCarville, Pardini, Vogel and Walton44], and under development on LMJ[Reference Troussel, Dennetiere, Maroni, Hoghoj, Hedacq, Cibik and Krumrey47]. In the following, we will present a novel diagnostic, based on lithium fluoride detectors.
The radiation may have an important effect on the RTI evolution in laser plasma experiments[Reference Huntington, Kuranz, Drake, Miles, Prisbrey, Park, Robey and Remington48] as well as in astrophysics[Reference Jacquet and Krumholz49]. Radiative shocks are a fundamental aspect of astrophysical and high energy density systems because any fast enough shock wave becomes radiative[Reference Bouquet, Stéhlé, Koenig, Chièze, Benuzzi-Mounaix, Batani, Leygnac, Fleury, Merdji, Michaut, Thais, Grandjouan, Hall, Henry and Lafon50, Reference Koenig, Vinci, Benuzzi-Mounaix, Ozaki, Ravasio, Rabec le Glohaec, Boireau, Michaut, Bouquet, Atzeni, Schiavi, Peyrusse and Batani51]. This happens because radiative energy fluxes increase stronger with the increasing shock velocity than kinetic and thermal energy fluxes do. Understanding the physical properties of radiative shock waves is fundamental since they are the basis of the interpretation of numerous astronomical observations, ranging from the magnetospherical accretion in young stellar objects to cataclysmic variables, and accreting neutron stars. In particular the Vishniac instability has been identified in the late radiative phase of evolution of a supernova remnant[Reference Blondin, Wright, Borkowski and Reynolds52]. Whereas the filaments observed in the Crab Nebulae could be due to RTI, observations of other supernovae (SN 1006, Cygnus Loop) have shown density and spatial fluctuations consistent with the predictions obtained in the linear regime of the Vishniac instability[Reference Raymond, Korreck, Sedlacek, Blair, Ghavamiam and Sankrit53]. Until now very few laboratory experiments have demonstrated instabilities at the front of radiative blast waves[Reference Osterhoff, Symes, Evens, Moore, Hellewell and Ditmire54]. While our work is primarily focused on young SNRs where radiation is not at play, a longer-term goal will be also to explore the effects of radiative losses. The radiative properties of the plasmas during the period of target acceleration and the RTI development could significantly modify the hydrodynamic characteristics. For example, during the nonlinear stage of RTI, the dense fluid forms elongated structures – spikes – penetrating in a light fluid. Then, if the mean free path of the photons emitted from the spike is greater than its characteristic diameter, the spike cools down, becomes denser and propagates faster due to the radiative losses. NIF and LMJ provide the unique opportunity to explore the combined effect of instability growth and radiative effects[Reference Pak, Divol, Gregori, Weber, Atherton, Bennedetti, Bradley, Callahan, Casey, Dewald, Döppner, Edwards, Frenje, Glenn, Grim, Hicks, Hsing, Izumi, Jones, Johnson, Khan, Kilkenny, Kline, Kyrala, Lindl, Landen, Le Pape, Ma, MacPhee, MacGowan, MacKinnon, Masse, Meezan, Moody, Olson, Ralph, Robey, Park, Remington, Ross, Tommasini, Town, Smalyuk, Glenzer and Moses55], promising to achieve the pressure-driven thin shell phase relevant for the Vishniac instability[Reference Michaut, Cavet, Bouquet, Rou and Nguyen56]. Extensive research on radiative shocks has been performed in the past decade, either theoretically[Reference Michaut, Falize, Cavet, Bouquet, Vinci, Reighard and Drake57] or experimentally on LULI2000[Reference Bouquet, Stéhlé, Koenig, Chièze, Benuzzi-Mounaix, Batani, Leygnac, Fleury, Merdji, Michaut, Thais, Grandjouan, Hall, Henry and Lafon50], Gekko XII[Reference Koenig, Michel, Yurchak, Michaut, Albertazzi, Laffite, Falize, Van Box Som, Sakawa, Sano, Hara, Morita, Kuramitsu, Barroso, Pelka, Gregori, Kodama, Ozaki, Lamb and Tzeferacos58], or Orion[Reference Suzuki-Vidal, Clayson, Stehlé, Swadling, Foster, Skidmore, Graham, Burdiak, Lebedev, Chaulagain, Singh, Gumbrell, Patankar, Spindloe, Larour, Kozlova, Rodriguez, Gil, Espinosa, Velarde and Danson59].
2.2.2 Experimental roadmap
Achieving accurate results within a few shots on a MJ laser facility is challenging and requires preliminary experiments and a step-by-step approach. In Europe, there is a wide spectrum and a high level of laser facilities (LULI2000, Vulcan, Orion) having a laser energy in the range of 1–2.5 kJ at
![]() $2\unicode[STIX]{x1D714}$
or
$2\unicode[STIX]{x1D714}$
or
![]() $3\unicode[STIX]{x1D714}$
(532 or 351 nm) to irradiate a planar package. These facilities are ideal to perform exploratory physics experiments, and to test advanced diagnostics concepts. We could also benefit from a high number of shots, and test various target designs. Preparatory experiments are mandatory because failure is not an option on MJ scale lasers. We are currently harnessing the continuum of laser energies on the European laser facilities. We develop a plurennial program on LULI2000 (see Section 3) and an Orion proposal in counterpropagating geometry has been recently selected. Facility time on OMEGA EP will also be purchased in 2019, because this 4 ns-beams facility is perfectly suited to perform test bed experiments in geometry similar to LMJ–PETAL envisioned configuration shown thereafter.
$3\unicode[STIX]{x1D714}$
(532 or 351 nm) to irradiate a planar package. These facilities are ideal to perform exploratory physics experiments, and to test advanced diagnostics concepts. We could also benefit from a high number of shots, and test various target designs. Preparatory experiments are mandatory because failure is not an option on MJ scale lasers. We are currently harnessing the continuum of laser energies on the European laser facilities. We develop a plurennial program on LULI2000 (see Section 3) and an Orion proposal in counterpropagating geometry has been recently selected. Facility time on OMEGA EP will also be purchased in 2019, because this 4 ns-beams facility is perfectly suited to perform test bed experiments in geometry similar to LMJ–PETAL envisioned configuration shown thereafter.
The final goal is to benefit both from the enhanced laser energy and the extended laser pulse duration (up to 30 ns) provided by LMJ to create a turbulent regime relevant for astrophysics mixing processes and SNRs. In fact, more laser energy allows first launching stronger shocks with high Mach numbers (
![]() $Ma=u/c$
where
$Ma=u/c$
where
![]() $u$
is the flow velocity and
$u$
is the flow velocity and
![]() $c$
the speed of sound in the material) in the range of 2–10[Reference Malamud, Shimony, Wan, Di Stefano, Elbaz, Kuranz, Keiter, Drake and Shvarts60]. On the other hand, a sustained laser drive will produce steady conditions that endure long enough to observe substantial instability growth, as done on NIF in indirect-drive[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38], or direct-drive[Reference Casner, Mailliet, Khan, Martinez, Izumi, Kalantar, Di Nicola, Di Nicola, Le Bel, Igumenshchev, Tikhonchuk, Remington, Masse and Smalyuk43], ablative RTI experiments[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38] as well as shock-shear platform[Reference Welser-Sherill, Fincke, Doss, Loomis, Flippo, Offermann, Keiter, Haines and Grinstein61, Reference Doss, Kline, Flippo, Perry, DeVolder, Tregillis, Loomis, Merritt, Murphy, Welser-Sherrill and Fincke62] and RM-reshock experiments[Reference Nagel, Raman, Huntington, MacLaren, Wang, Barrios, Baumann, Bender, Benedetti, Doane, Felker, Fitzsimmons, Flippo, Holder, Kaczala, Perry, Seugling, Savage and Zhou63].
$c$
the speed of sound in the material) in the range of 2–10[Reference Malamud, Shimony, Wan, Di Stefano, Elbaz, Kuranz, Keiter, Drake and Shvarts60]. On the other hand, a sustained laser drive will produce steady conditions that endure long enough to observe substantial instability growth, as done on NIF in indirect-drive[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38], or direct-drive[Reference Casner, Mailliet, Khan, Martinez, Izumi, Kalantar, Di Nicola, Di Nicola, Le Bel, Igumenshchev, Tikhonchuk, Remington, Masse and Smalyuk43], ablative RTI experiments[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38] as well as shock-shear platform[Reference Welser-Sherill, Fincke, Doss, Loomis, Flippo, Offermann, Keiter, Haines and Grinstein61, Reference Doss, Kline, Flippo, Perry, DeVolder, Tregillis, Loomis, Merritt, Murphy, Welser-Sherrill and Fincke62] and RM-reshock experiments[Reference Nagel, Raman, Huntington, MacLaren, Wang, Barrios, Baumann, Bender, Benedetti, Doane, Felker, Fitzsimmons, Flippo, Holder, Kaczala, Perry, Seugling, Savage and Zhou63].
The LMJ target design is scaled from astrophysical observations. Optimization will be performed to maximize the number of RTI e-foldings of a modulated heavy-light interface in deceleration in a light medium. Preliminary experiments on LULI2000 allow testing the target geometry and material, and benchmarking the simulations chain up to the weakly to highly nonlinear stage of the RTI. Final LMJ experiments will enable turbulent HED plasma truly relevant for young SNRs. Figure 3 summarizes our experimental strategy, phased with the numerical capabilities to simulate HED flows with increasing complexity. We focus in the next section on recent results acquired on LULI2000, as a stepping stone toward a MJ design.
3 Preliminary novel results acquired on LULI2000
3.1 Experimental setup and the first radiographs
Numerous experiments relevant for laboratory astrophysics have been performed at LULI[Reference Bouquet, Stéhlé, Koenig, Chièze, Benuzzi-Mounaix, Batani, Leygnac, Fleury, Merdji, Michaut, Thais, Grandjouan, Hall, Henry and Lafon50, Reference Koenig, Vinci, Benuzzi-Mounaix, Ozaki, Ravasio, Rabec le Glohaec, Boireau, Michaut, Bouquet, Atzeni, Schiavi, Peyrusse and Batani51, Reference Gregori, Ravasio, Murphy, Schaar, Baird, Bell, Benuzzi-Mounaix, Bingham, Constantin, Drake, Edwards, Everson, Gregory, Kuramitsu, Lau, Niemann, Park, Remington, Reville, Robinson, Ryutov, SAkawa, Yang, Woolsey, Koenig and Miniati64, Reference Yurchak, Ravasio, Pelka, Pikuz, Falize, Vinci, Koenig, Loupias, Benuzzi-Mounaix, Fatenejad, Tzeferacos, Lamb and Blackman65]. The limited available laser energy and pulse duration (typically 1.5 kJ per beam at
![]() $1\unicode[STIX]{x1D714}$
in 1 ns pulse) do not allow entering into the nonlinear regime for RTI in acceleration. Therefore, we have designed an RTI experiment in deceleration[Reference Bose, Woo, Nora and Betti66]. The LULI2000 experimental configuration is described in Figure 4 above. A composite modulated package with rear side modulations (
$1\unicode[STIX]{x1D714}$
in 1 ns pulse) do not allow entering into the nonlinear regime for RTI in acceleration. Therefore, we have designed an RTI experiment in deceleration[Reference Bose, Woo, Nora and Betti66]. The LULI2000 experimental configuration is described in Figure 4 above. A composite modulated package with rear side modulations (
![]() $\unicode[STIX]{x1D706}=120~\unicode[STIX]{x03BC}\text{m}$
wavelength,
$\unicode[STIX]{x1D706}=120~\unicode[STIX]{x03BC}\text{m}$
wavelength,
![]() $20~\unicode[STIX]{x03BC}\text{m}$
peak-to-valley amplitude) is driven by the north beam at full energy (400 J) in a 1.5 ns square pulse. The package decelerates into a lighter medium, typically a 100 or 200 mg/cc resorcinol formaldehyde foam (
$20~\unicode[STIX]{x03BC}\text{m}$
peak-to-valley amplitude) is driven by the north beam at full energy (400 J) in a 1.5 ns square pulse. The package decelerates into a lighter medium, typically a 100 or 200 mg/cc resorcinol formaldehyde foam (
![]() $\text{C}_{15}\text{H}_{12}\text{O}_{4}$
), triggering the development of RTI in the deceleration phase. Such targets require micromachining, precise assembly (embedded layers) and specific materials (doped brominated plastic). The Pico2000 beam is used in bottom-up geometry[Reference Brambrink, Baton, Koenig, Yurchak, Bidaut, Albertazzi, Cross, Gregori, Rigby, Falize, Pelka, Kroll, Pikuz, Sakawa, Ozaki, Kuranz, Manuel, Li, Tzeferacos and Lamb67] to acquire snapshots of RTI during the linear and highly nonlinear phases. We are interested in accurate measurement of the mixing zone width in the nonlinear stage[Reference Swisher, Kuranz, Arnett, Hurricane, Remington, Robey and Abarzhi68]. The main advantage of a few weeks’ campaigns on LULI is to test ideas for target designs and the capability to drive those targets in the relevant plasma regimes. Many diagnostics are available on LULI2000, going from visible diagnostics to X-ray or even particle beams. We concentrate here on X-rays imaging diagnostics. Typical radiographs acquired during the first RTI campaign are shown in Figure 5, for the two foam densities used.
$\text{C}_{15}\text{H}_{12}\text{O}_{4}$
), triggering the development of RTI in the deceleration phase. Such targets require micromachining, precise assembly (embedded layers) and specific materials (doped brominated plastic). The Pico2000 beam is used in bottom-up geometry[Reference Brambrink, Baton, Koenig, Yurchak, Bidaut, Albertazzi, Cross, Gregori, Rigby, Falize, Pelka, Kroll, Pikuz, Sakawa, Ozaki, Kuranz, Manuel, Li, Tzeferacos and Lamb67] to acquire snapshots of RTI during the linear and highly nonlinear phases. We are interested in accurate measurement of the mixing zone width in the nonlinear stage[Reference Swisher, Kuranz, Arnett, Hurricane, Remington, Robey and Abarzhi68]. The main advantage of a few weeks’ campaigns on LULI is to test ideas for target designs and the capability to drive those targets in the relevant plasma regimes. Many diagnostics are available on LULI2000, going from visible diagnostics to X-ray or even particle beams. We concentrate here on X-rays imaging diagnostics. Typical radiographs acquired during the first RTI campaign are shown in Figure 5, for the two foam densities used.
The nonlinear development stage of RTI is evidenced with the classical development of mushrooms at the spikes heads at late time (see for example
![]() $t=30$
and 35 ns data). FLASH simulations were performed by one of us and will be published elsewhere[Reference Rigon, Casner, Albertazzi and Koenig69]. FLASH is a multiphysics AMR (adaptative mesh refinement), radiation- magnetohydrodynamic code developed in the University of Chicago. FLASH is able to simulate not only a wide range of high energy density physics experiments[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb42], but also astrophysical objects as it is originally dedicated to supernovae physics studies. In our case, 2D FLASH simulations recover the global shape of the interface (due to the
$t=30$
and 35 ns data). FLASH simulations were performed by one of us and will be published elsewhere[Reference Rigon, Casner, Albertazzi and Koenig69]. FLASH is a multiphysics AMR (adaptative mesh refinement), radiation- magnetohydrodynamic code developed in the University of Chicago. FLASH is able to simulate not only a wide range of high energy density physics experiments[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Flocke, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, Weide, White, Reville, Miniati, Schekochihin, Froula, Gregori and Lamb42], but also astrophysical objects as it is originally dedicated to supernovae physics studies. In our case, 2D FLASH simulations recover the global shape of the interface (due to the
![]() $500~\unicode[STIX]{x03BC}\text{m}$
focal spot RPP), as well as the nonlinear RTI growth (see Figure 6). The spatial resolution currently achievable with point projection radiography (
$500~\unicode[STIX]{x03BC}\text{m}$
focal spot RPP), as well as the nonlinear RTI growth (see Figure 6). The spatial resolution currently achievable with point projection radiography (
![]() $25~\unicode[STIX]{x03BC}\text{m}$
) and imaging plate (IP) detectors is not sufficient to resolve the details of the mixing zone, and the roll-up of the spikes due to the KHI[Reference Smalyuk, Hansen, Hurricane, Langstaff, Martinez, Park, Raman, Remington, Robey, Schilling, Wallace, Elbaz, Shimony, Shvarts, Di Stefano, Drake, Marion, Kraul and Kuranz8]. Further experiments will concentrate on the Atwood dependence of RTI growth in the nonlinear phase, in order to evidence the reacceleration phase of the RTI. In fact, the single-mode RTI is still the focus of research on experimental and numerical studies.[Reference Ramaprabhu, Dimonte, Woodward, Fryer, Rockefeller, Muthuraman, Lin and Jayaraj70]. To do so, we need to develop advanced X-ray diagnostics which provide at least
$25~\unicode[STIX]{x03BC}\text{m}$
) and imaging plate (IP) detectors is not sufficient to resolve the details of the mixing zone, and the roll-up of the spikes due to the KHI[Reference Smalyuk, Hansen, Hurricane, Langstaff, Martinez, Park, Raman, Remington, Robey, Schilling, Wallace, Elbaz, Shimony, Shvarts, Di Stefano, Drake, Marion, Kraul and Kuranz8]. Further experiments will concentrate on the Atwood dependence of RTI growth in the nonlinear phase, in order to evidence the reacceleration phase of the RTI. In fact, the single-mode RTI is still the focus of research on experimental and numerical studies.[Reference Ramaprabhu, Dimonte, Woodward, Fryer, Rockefeller, Muthuraman, Lin and Jayaraj70]. To do so, we need to develop advanced X-ray diagnostics which provide at least
![]() $10~\unicode[STIX]{x03BC}\text{m}$
(or
$10~\unicode[STIX]{x03BC}\text{m}$
(or
![]() $5~\unicode[STIX]{x03BC}\text{m}$
) spatial resolution, in order to resolve tiny details for more elongated spikes, or sophisticated multimode profile. That is the reason why we are exploring the potentialities of LiF detectors as transformative X-ray diagnostics for HEDP experiments[Reference Ya. Faenov, Kato, Tanaka, Kishimoto, Ishino, Nishikino, Fukuda, Bulanov and Kawachi71, Reference Pikuz, Faenov, Matsuoka, Matsuyama, Yamauchi, Ozaki, Albertazzi, Inubushi, Yabashi, Tono, Sato, Yumoto, Ohashi, Pikuz, Grum-Grzhimailo, Nishikino, Kawachi, Ishikawa and Kodama72].
$5~\unicode[STIX]{x03BC}\text{m}$
) spatial resolution, in order to resolve tiny details for more elongated spikes, or sophisticated multimode profile. That is the reason why we are exploring the potentialities of LiF detectors as transformative X-ray diagnostics for HEDP experiments[Reference Ya. Faenov, Kato, Tanaka, Kishimoto, Ishino, Nishikino, Fukuda, Bulanov and Kawachi71, Reference Pikuz, Faenov, Matsuoka, Matsuyama, Yamauchi, Ozaki, Albertazzi, Inubushi, Yabashi, Tono, Sato, Yumoto, Ohashi, Pikuz, Grum-Grzhimailo, Nishikino, Kawachi, Ishikawa and Kodama72].
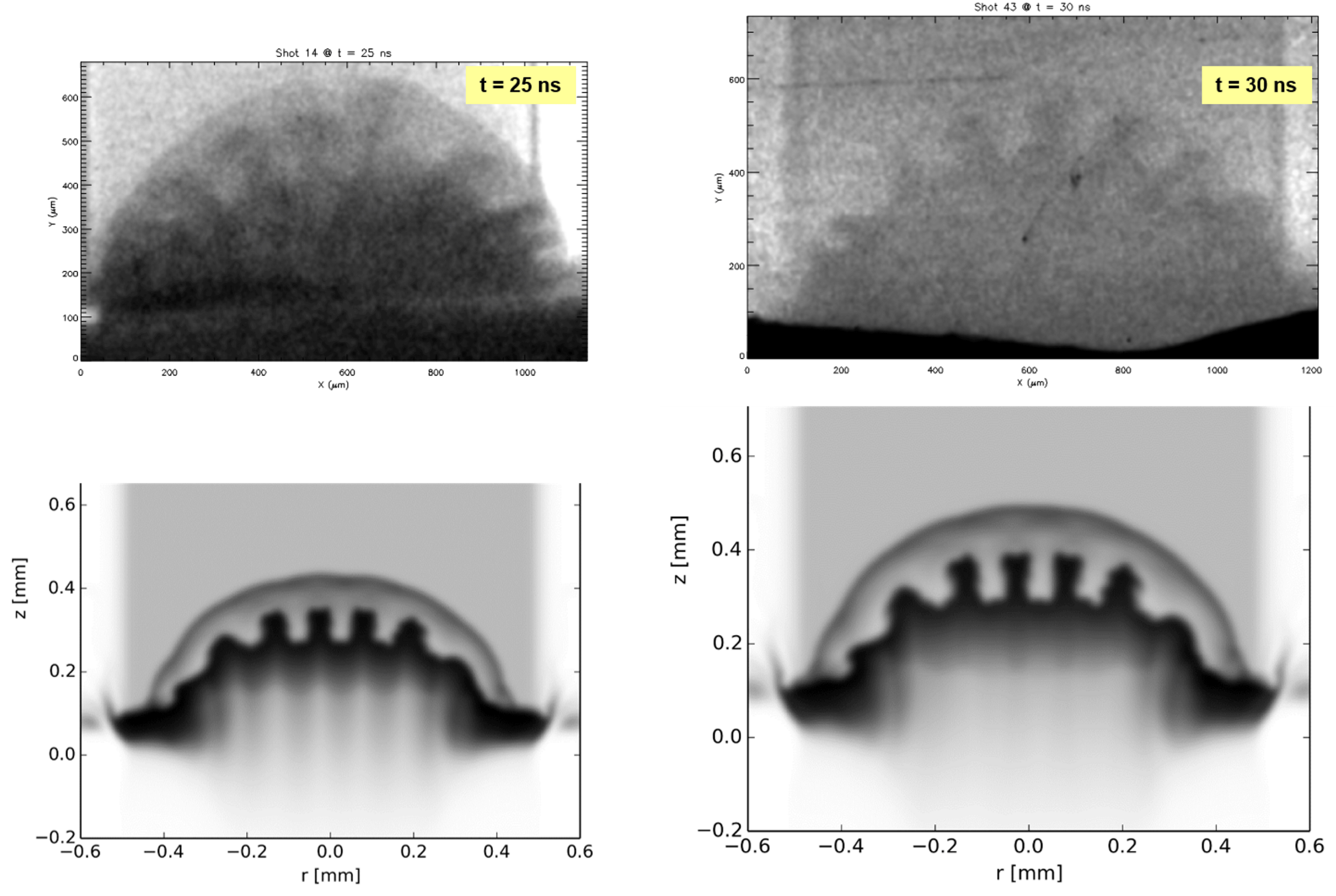
Figure 6. Comparison of experimental (first row) and postprocessed FLASH hydrodynamics simulations (second row).
3.2 Development of advanced X-ray diagnostic methods
To achieve measurements of the mass density distribution, X-ray radiography is the most relevant diagnostic. For that purpose, good temporal (
![]() ${<}$
100 ps) and spatial (
${<}$
100 ps) and spatial (
![]() ${<}10~\unicode[STIX]{x03BC}\text{m}$
) resolutions and a high flux of photons (
${<}10~\unicode[STIX]{x03BC}\text{m}$
) resolutions and a high flux of photons (
![]() $10^{10}{-}10^{14}$
photons) are necessary. We performed in 2016 the first tests of LiF-based detectors on an HED laser experiment. LiF-based X-ray imaging detectors have been yet tested for soft and hard X-rays (up to 10 keV)[Reference Pikuz, Faenov, Matsuoka, Matsuyama, Yamauchi, Ozaki, Albertazzi, Inubushi, Yabashi, Tono, Sato, Yumoto, Ohashi, Pikuz, Grum-Grzhimailo, Nishikino, Kawachi, Ishikawa and Kodama72]. Due to a very high spatial resolution over a large field of view, wide dynamic range and simplicity of use, LiF-based detectors are particularly suitable for the development of table-top X-ray microscopy systems. The X-ray exposure of a sample, placed close to the LiF surface, induces the formation of color centers (CCs), whose density is locally proportional to the intensity of the radiation transmitted through the investigated object. LiF has an intrinsic spatial resolution related to the physical dimensions of CCs (that are at atomic scale (
$10^{10}{-}10^{14}$
photons) are necessary. We performed in 2016 the first tests of LiF-based detectors on an HED laser experiment. LiF-based X-ray imaging detectors have been yet tested for soft and hard X-rays (up to 10 keV)[Reference Pikuz, Faenov, Matsuoka, Matsuyama, Yamauchi, Ozaki, Albertazzi, Inubushi, Yabashi, Tono, Sato, Yumoto, Ohashi, Pikuz, Grum-Grzhimailo, Nishikino, Kawachi, Ishikawa and Kodama72]. Due to a very high spatial resolution over a large field of view, wide dynamic range and simplicity of use, LiF-based detectors are particularly suitable for the development of table-top X-ray microscopy systems. The X-ray exposure of a sample, placed close to the LiF surface, induces the formation of color centers (CCs), whose density is locally proportional to the intensity of the radiation transmitted through the investigated object. LiF has an intrinsic spatial resolution related to the physical dimensions of CCs (that are at atomic scale (
![]() ${\sim}$
1 nm)). After an X-ray exposition, the image stored and stable for very long time can be read out just illuminating the detector with a blue light; the latter is accompanied by visible photoluminescence signal to be observed via an optical microscope.
${\sim}$
1 nm)). After an X-ray exposition, the image stored and stable for very long time can be read out just illuminating the detector with a blue light; the latter is accompanied by visible photoluminescence signal to be observed via an optical microscope.
The experimental setup on LULI2000 is shown in Figure 4, together with spatial resolution tests performed with Cu resolution grids (300, 600 and 1000 lines per inch). A spatial resolution of
![]() $\unicode[STIX]{x1D6FF}$
R
$\unicode[STIX]{x1D6FF}$
R
![]() $_{\text{S}}$
$_{\text{S}}$
![]() ${\sim}3~\unicode[STIX]{x03BC}\text{m}$
was measured (see Figure 7). IP and LiF detectors were compared on side-on radiograph of a (undriven) modulated target (see Figure 8). Despite a smaller contrast, a spatial resolution of
${\sim}3~\unicode[STIX]{x03BC}\text{m}$
was measured (see Figure 7). IP and LiF detectors were compared on side-on radiograph of a (undriven) modulated target (see Figure 8). Despite a smaller contrast, a spatial resolution of
![]() $\unicode[STIX]{x1D6FF}\text{R}_{\text{S}}\sim 7~\unicode[STIX]{x03BC}\text{m}$
is measured with the LiF, compared to
$\unicode[STIX]{x1D6FF}\text{R}_{\text{S}}\sim 7~\unicode[STIX]{x03BC}\text{m}$
is measured with the LiF, compared to
![]() $\unicode[STIX]{x1D6FF}\text{R}_{\text{S}}\sim 30~\unicode[STIX]{x03BC}\text{m}$
with IP. Unfortunately this enhanced spatial resolution was only demonstrated for static (undriven) modulated targets. We still need to optimize the shielding of the detector and understand better its sensitivity to the broadband X-ray continuum created by the ns irradiation of the main target.
$\unicode[STIX]{x1D6FF}\text{R}_{\text{S}}\sim 30~\unicode[STIX]{x03BC}\text{m}$
with IP. Unfortunately this enhanced spatial resolution was only demonstrated for static (undriven) modulated targets. We still need to optimize the shielding of the detector and understand better its sensitivity to the broadband X-ray continuum created by the ns irradiation of the main target.

Figure 7. Experimental configuration and typical radiographs acquired with LiF crystals on LULI2000 of a 1000 lines per inch (lpi) copper grid.

Figure 8. Comparison of LiF and IP images for the same (undriven) modulated target. The spatial resolution is estimated to be
![]() $7~\unicode[STIX]{x03BC}\text{m}$
in the LiF case, compared to
$7~\unicode[STIX]{x03BC}\text{m}$
in the LiF case, compared to
![]() $30~\unicode[STIX]{x03BC}\text{m}$
with IP.
$30~\unicode[STIX]{x03BC}\text{m}$
with IP.
These detectors were used on a recent run on the SACLA XFEL beam (@10.1 keV) by some of us[Reference Faenov73]. The very bright and monochromatic X-ray emission is of course favorable for phase-contrast imaging. The LULI2000 RTI targets were imaged on LiF with SACLA XFEL used as a backlighter. By demonstrating for the capabilities of LiF crystals, these passive detectors may constitute promising imaging systems for PW facilities such as LMJ-PETAL[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel12]. Based on the LULI2000 experiments, we present thereafter the design of a novel experimental platform for future experiments on LMJ–PETAL, in accordance with the near-term capabilities of the facility[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel12, 29].
4 Development of LMJ–PETAL direct-drive platform
4.1 LMJ–PETAL experimental platform
The first physics experiments on LMJ have been performed at the end of 2014 with 2 quadruplets (8 beams), and a total laser energy on target of 20 kJ [Reference Miquel74]. The first diagnostic installed in 2014 on LMJ is a gated X-ray imager with grazing incidence mirrors, which provides a spatial resolution of
![]() $30~\unicode[STIX]{x03BC}\text{m}$
in a 3 mm field of view[Reference Rosch, Rosch, Trosseille, Caillaud, Allouche, Bourgade, Briat, Brunel, Burillo, Casner, Depierreux, Gontier, Jadaud, Le Breton, Llavador, Loupias, Miquel, Oudot, Perez, Raimbourg, Rousseau, Rousseaux, Rubbelynck, Stemmler, Troussel, Ulmer, Wrobel, Beauvais, Pallet and Prevot46]. The experimental capabilities of LMJ (number of beams and type of plasma diagnostics) will increase gradually during the following years. The PETAL beam[Reference Blanchot, Béhar, Chapuis, Chappuis, Chardavoine, Charrier, Coïc, Damiens-Dupont, Duthu, Garcia, Goossens, Granet, Grosset-Grange, Guerin, Hebrard, Hilsz, Lamaignere, Lacombe, Lavastre, Longhi, Luce, Macias, Mangeant, Mazataud, Minou, Morgaint, Noailles, Neauport, Patelli, Perrot-Minnot, Present, Remy, Rouyer, Santacreu, Sozet, Valla and Laniesse75] consists in the addition of one short-pulse (500 fs–10 ps) ultra-high-power, high energy beam (a few kJ compressed energy) to the LMJ facility[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel12]. PETAL, commissioned at the end of 2016, extends the LMJ diagnostic capabilities to radiography with energetic particles (protons/ions/electrons) in the 0.1–200 MeV range[Reference Rabhi, Batani, Boutoux, Ducret, Jakubowska, Lantuejoul-Thfoin, Nauraye, Patriarca, Saïd, Semsoum, Serani, Thomas and Vauzour76]. In particular, the point projection proton radiography[Reference Zylstra, Li, Rinderknecht, Séguin, Petrasso, Stoeckl, Meyerhofer, Nilson, Sangster, Le Pape, Mackinnon and Patel77] could be of interest for our purpose.
$30~\unicode[STIX]{x03BC}\text{m}$
in a 3 mm field of view[Reference Rosch, Rosch, Trosseille, Caillaud, Allouche, Bourgade, Briat, Brunel, Burillo, Casner, Depierreux, Gontier, Jadaud, Le Breton, Llavador, Loupias, Miquel, Oudot, Perez, Raimbourg, Rousseau, Rousseaux, Rubbelynck, Stemmler, Troussel, Ulmer, Wrobel, Beauvais, Pallet and Prevot46]. The experimental capabilities of LMJ (number of beams and type of plasma diagnostics) will increase gradually during the following years. The PETAL beam[Reference Blanchot, Béhar, Chapuis, Chappuis, Chardavoine, Charrier, Coïc, Damiens-Dupont, Duthu, Garcia, Goossens, Granet, Grosset-Grange, Guerin, Hebrard, Hilsz, Lamaignere, Lacombe, Lavastre, Longhi, Luce, Macias, Mangeant, Mazataud, Minou, Morgaint, Noailles, Neauport, Patelli, Perrot-Minnot, Present, Remy, Rouyer, Santacreu, Sozet, Valla and Laniesse75] consists in the addition of one short-pulse (500 fs–10 ps) ultra-high-power, high energy beam (a few kJ compressed energy) to the LMJ facility[Reference Casner, Caillaud, Darbon, Duval, Thfouin, Jadaud, LeBreton, Reverdin, Rosse, Rosch, Blanchot, Villette, Wrobel and Miquel12]. PETAL, commissioned at the end of 2016, extends the LMJ diagnostic capabilities to radiography with energetic particles (protons/ions/electrons) in the 0.1–200 MeV range[Reference Rabhi, Batani, Boutoux, Ducret, Jakubowska, Lantuejoul-Thfoin, Nauraye, Patriarca, Saïd, Semsoum, Serani, Thomas and Vauzour76]. In particular, the point projection proton radiography[Reference Zylstra, Li, Rinderknecht, Séguin, Petrasso, Stoeckl, Meyerhofer, Nilson, Sangster, Le Pape, Mackinnon and Patel77] could be of interest for our purpose.
Figure 9(a) displays the LMJ power versus energy diagram. Our design is based on conservative estimates of available laser energy (10–15 kJ per quadruplet in 3 ns square laser pulse). The envisioned laser configuration of our LMJ direct-drive experiments is schematically drawn in Figure 9(b). It takes advantage of the nominal north/south polar beams configuration of LMJ 6–8 lower quadruplets (60–90 kJ of laser energy) and will be used to accelerate the planar package. The upper quadruplets irradiate the face-on (blue beams in Figure 9(b)) and the side-on backlighter foils. At that moment, the main diagnostic considered is the enhanced resolution hard X-ray imager (ERHXI)[Reference Troussel, Villette, Emprin, Oudot, Tassin, Bridou, Delmotte and Krumrey78] inserted in the polar north inserter. The side-on radiography will provide information about shock planarity, deceleration and 2D density maps of the turbulent mixing zone. We build from results acquired on NIF for the long duration planar direct-drive platform recently commissioned[Reference Casner, Mailliet, Khan, Martinez, Izumi, Kalantar, Di Nicola, Di Nicola, Le Bel, Igumenshchev, Tikhonchuk, Remington, Masse and Smalyuk43]. Due to the large laser spot available (up to
![]() $1500~\unicode[STIX]{x03BC}\text{m}$
in diameter), shock bowing and the detrimental effects of rarefaction waves propagating back from the lateral sides of the target are minimized. The laser imprint perturbation[Reference Smalyuk, Goncharov, Boehly, Delettrez, Li, J., Marozas, Maximov, Meyerhofer, Regan and Sangster79, Reference Delorme, Olazabal-Loumé, Casner, Nicolaï, Borisenko, Breil, Froula, Fujioka, Goncharov, Grech, Michel, Orekhov, Riazuelo, Seka, Sunahara and Tikhonchuk80] is not a limiting factor in such experiments because we concentrate on the RTI at an embedded interface. The laser induced small scale perturbations at the ablation surface (laser speckles of a few
$1500~\unicode[STIX]{x03BC}\text{m}$
in diameter), shock bowing and the detrimental effects of rarefaction waves propagating back from the lateral sides of the target are minimized. The laser imprint perturbation[Reference Smalyuk, Goncharov, Boehly, Delettrez, Li, J., Marozas, Maximov, Meyerhofer, Regan and Sangster79, Reference Delorme, Olazabal-Loumé, Casner, Nicolaï, Borisenko, Breil, Froula, Fujioka, Goncharov, Grech, Michel, Orekhov, Riazuelo, Seka, Sunahara and Tikhonchuk80] is not a limiting factor in such experiments because we concentrate on the RTI at an embedded interface. The laser induced small scale perturbations at the ablation surface (laser speckles of a few
![]() $\unicode[STIX]{x03BC}$
m in diameter) are smoothed out when the shock arrives at the modulated rear target side. In that regard, our target design is different and less insensitive to imprint compared to inertial confinement fusion direct-drive implosions[Reference Hu, Michel, Davis, Betti, Radha, Campbell, Froula and Stoeckl81], where the shocks travel only small distances and feed in the perturbations across the shell.
$\unicode[STIX]{x03BC}$
m in diameter) are smoothed out when the shock arrives at the modulated rear target side. In that regard, our target design is different and less insensitive to imprint compared to inertial confinement fusion direct-drive implosions[Reference Hu, Michel, Davis, Betti, Radha, Campbell, Froula and Stoeckl81], where the shocks travel only small distances and feed in the perturbations across the shell.
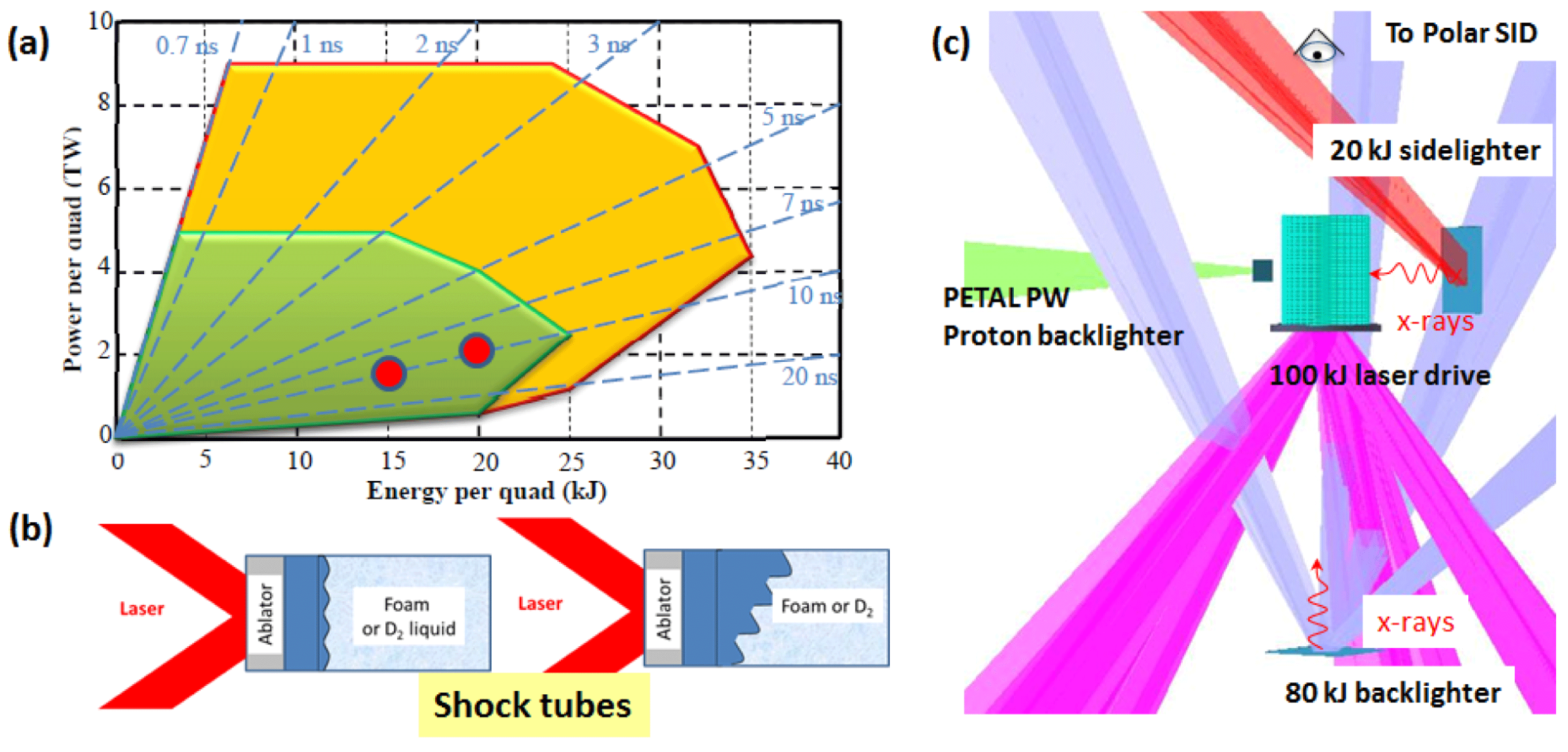
Figure 9. (a) Energy-power diagram for one LMJ quadruplet. The green area is the operating zone without noticeable optical damages. (b) Typical LMJ experimental configuration. Lower quads are used to accelerate the package, whereas upper quads irradiate the face-on and side-on backlighters. (c) Shock tube target designs.
The PETAL probe beam is not a primary diagnostic tool for this project. However the side-on proton radiography could be valuable to image the self-generated magnetic field structure. The RTI turbulent mixing layer could create intense self-generated magnetic fields[Reference Srinivasan and Tang82] that grow in time as the instability progresses. The primary source of this field in the generalized Ohm’s law is the vector product of gradients of the electron temperature and density (the Biermann battery effect)[Reference Bierrman83]. The Biermann battery by itself is not sufficient to generate observable magnetic fields. Dynamo amplification by turbulent plasma flows is necessary to create measurable magnetic fields[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori84]. A turbulent magnetic field created for the first time in HED plasmas from hydrodynamics instabilities (and not colliding flows[Reference Tzeferacos, Rigby, Bott, Bell, Bingham, Casner, Cattaneo, Churazov, Emig, Fiuza, Forest, Foster, Graziani, Katz, Koenig, Li, Meinecke, Petrasso, Park, Remington, Ross, Ryu, Ryutov, White, Reville, Miniati, Schekochihin, Lamb, Froula and Gregori84]) could potentially be probed with the PETAL generated proton beam by radiographing the turbulent zone. The proton spectrum and angular distribution could be with the SEPAGE diagnostic[Reference Ducret, Batani, Boutoux, Chancé, Gastineau, Guillard, Harrault, Jakubowska, Lantuejoul-Thfoin, Leboeuf, Loiseau, Lotode, Pès, Rabhi, Saïd, Semsoum, Serani, Thomas, Toussaint and Vauzour85] on a reference shot. Hence the proton beam will propagate across the turbulent mixing zone on a second shot, and the proton spectrum is compared to the reference, providing reproducibility in laser condition.
4.2 Postprocessed simulations
We rely on target design simulations performed with FLASH. We leverage the results of LULI2000 and use theoretical scaling laws[Reference Falize, Michaut and Bouquet7] to define the most relevant LMJ experiments to create turbulent HED plasmas relevant for young SNRs[Reference Swisher, Kuranz, Arnett, Hurricane, Remington, Robey and Abarzhi68]. Extensive simulations are performed using realistic EOS for the brominated pusher and the foam[Reference Benuzzi, Koenig, Krishnan, Faral, Nazarov, Temporal, Batani, Müller, Torsiello, Hall and Grandjouan86]. Furthermore, these calculations are benchmarked against the results of LULI2000 experiments[Reference Rigon, Casner, Albertazzi and Koenig69]. The laser conditions are 60 kJ of laser drive, with a 3 ns square pulse. The peak laser intensity taken into account is
![]() $6\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$
with a super-Gaussian distribution. The target geometry is shown in Figure 9(c). The shock tube has a diameter of 3 mm and is filled with a CHO foam (0.1 mg/cc). The ablator is
$6\times 10^{14}~\text{W}\cdot \text{cm}^{-2}$
with a super-Gaussian distribution. The target geometry is shown in Figure 9(c). The shock tube has a diameter of 3 mm and is filled with a CHO foam (0.1 mg/cc). The ablator is
![]() $100~\unicode[STIX]{x03BC}\text{m}$
thick with internal modulation.
$100~\unicode[STIX]{x03BC}\text{m}$
thick with internal modulation.
Preliminary simulations are performed starting from a multimode internal modulation (cf. Figure 10). The multimode considered here is the sum of 3 wavelengths (
![]() $33~\unicode[STIX]{x03BC}\text{m}$
,
$33~\unicode[STIX]{x03BC}\text{m}$
,
![]() $70~\unicode[STIX]{x03BC}\text{m}$
and
$70~\unicode[STIX]{x03BC}\text{m}$
and
![]() $100~\unicode[STIX]{x03BC}\text{m}$
, with the same peak-to-valley amplitude of
$100~\unicode[STIX]{x03BC}\text{m}$
, with the same peak-to-valley amplitude of
![]() $6~\unicode[STIX]{x03BC}\text{m}$
and different phases). The multimode perturbation will include more modes (as done for the ablative RTI experiments[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38]) in the future. The large dimensions of the target allow keeping a flat central zone without the detrimental effects of rarefaction waves. Starting from this complex pattern gives birth to mode coupling[Reference Miles, Edwards, Blue, Hansen, Robey, Drake, Kuranz and Leibrandt87] and the development of a turbulent mixing zone (TMZ) at late time. The simulations are postprocessed for titanium
$6~\unicode[STIX]{x03BC}\text{m}$
and different phases). The multimode perturbation will include more modes (as done for the ablative RTI experiments[Reference Casner, Smalyuk, Masse, Igumenshchev, Liberatore, Jacquet, Chicanne, Loiseau, Poujade, Bradley, Park and Remington10, Reference Casner, Masse, Martinez, Liberatore, Loiseau, Masson-Laborde, Jacquet, Moore, Seugling, Felker, Farrell, Giraldez, Nikroo, Haan, Remington and Smalyuk36–Reference Martinez, Smalyuk, Kane, Casner, Liberatore and Masse38]) in the future. The large dimensions of the target allow keeping a flat central zone without the detrimental effects of rarefaction waves. Starting from this complex pattern gives birth to mode coupling[Reference Miles, Edwards, Blue, Hansen, Robey, Drake, Kuranz and Leibrandt87] and the development of a turbulent mixing zone (TMZ) at late time. The simulations are postprocessed for titanium
![]() $\text{K}\unicode[STIX]{x03B1}$
sidelighter energy (Figure 10) and 2 different spatial resolutions of the ERXHI gated imager R
$\text{K}\unicode[STIX]{x03B1}$
sidelighter energy (Figure 10) and 2 different spatial resolutions of the ERXHI gated imager R
![]() $_{\text{S}}$
(R
$_{\text{S}}$
(R
![]() $_{\text{S}}\sim 5$
and
$_{\text{S}}\sim 5$
and
![]() $10~\unicode[STIX]{x03BC}\text{m}$
as specified in the LMJ Users Guide[29]). As can be seen in Figure 10(e), the tips of the spikes are better resolved with
$10~\unicode[STIX]{x03BC}\text{m}$
as specified in the LMJ Users Guide[29]). As can be seen in Figure 10(e), the tips of the spikes are better resolved with
![]() $5~\unicode[STIX]{x03BC}\text{m}$
spatial resolution. The TMZ width is defined according to Refs. [Reference Kuranz, Drake, Grosskopf, Fryxell, Budde, Hansen, Miles, Plewa, Hearn and Knauer23, Reference Brambrink, Baton, Koenig, Yurchak, Bidaut, Albertazzi, Cross, Gregori, Rigby, Falize, Pelka, Kroll, Pikuz, Sakawa, Ozaki, Kuranz, Manuel, Li, Tzeferacos and Lamb67] as the average height between the spikes and bubbles. The principal metric of our experiment will therefore be the measurement of the forward shock position, and the growth of the TMZ width versus time.
$5~\unicode[STIX]{x03BC}\text{m}$
spatial resolution. The TMZ width is defined according to Refs. [Reference Kuranz, Drake, Grosskopf, Fryxell, Budde, Hansen, Miles, Plewa, Hearn and Knauer23, Reference Brambrink, Baton, Koenig, Yurchak, Bidaut, Albertazzi, Cross, Gregori, Rigby, Falize, Pelka, Kroll, Pikuz, Sakawa, Ozaki, Kuranz, Manuel, Li, Tzeferacos and Lamb67] as the average height between the spikes and bubbles. The principal metric of our experiment will therefore be the measurement of the forward shock position, and the growth of the TMZ width versus time.
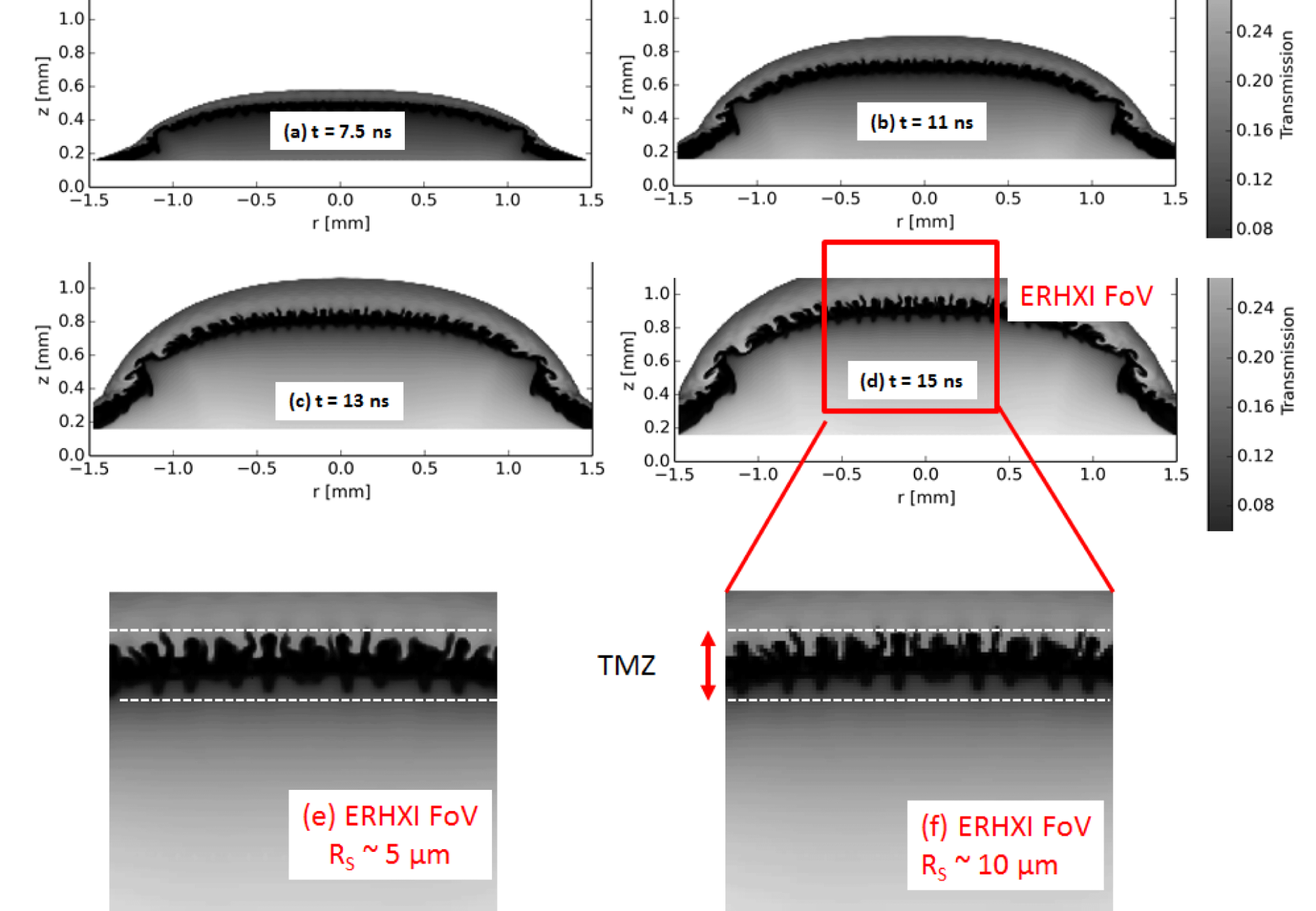
Figure 10. (a) to (d) Postprocessed radiographs of RTI multimode evolution with a titanium backlighter according to ERHXI spatial resolution of
![]() $10~\unicode[STIX]{x03BC}\text{m}$
. (e) and (f) Comparison of ERHXI field of view with spacial resolution of
$10~\unicode[STIX]{x03BC}\text{m}$
. (e) and (f) Comparison of ERHXI field of view with spacial resolution of
![]() $5~\unicode[STIX]{x03BC}\text{m}$
and
$5~\unicode[STIX]{x03BC}\text{m}$
and
![]() $10~\unicode[STIX]{x03BC}\text{m}$
. The tips of the spikes are better resolved in (e). The turbulent mixing zone width is defined as the average distance between the RTI spike and bubbles.
$10~\unicode[STIX]{x03BC}\text{m}$
. The tips of the spikes are better resolved in (e). The turbulent mixing zone width is defined as the average distance between the RTI spike and bubbles.
Some remembering of the initial conditions is still visible in the simulations in Figure 10. The multimode profile needs to include more wavelengths, and the simulations pursued later in time. The precise details of laser ‘shock tubes’ configurations (material, thicknesses, density and nature of the low-density medium) will be refined depending on the results of future experiments scheduled on Orion and OMEGA EP. The inclined RTI/KHI configuration shown in Figure 9(c) could be tested. It is interesting because the oblique shock propagation in compressible fluids gives birth to complicated flows including Mach stem wave generation[Reference Ben-Dor88] of importance for certain emission features in Herbig–Haro objects[Reference Hartigan, Franck, Foster, Wilde, Douglas, Rosen, Coker, Blue and Hansen89].
5 Summary and perspectives
The TurboHEDP project aims at shedding light on turbulent HED plasmas in the laboratory, enabling progress in the simulation and modeling of these complex flows in conditions relevant for laboratory astrophysics. The dawn of MJ scale laser facilities truly enables creating for the first time highly nonlinear flows of dense plasmas. Whereas preliminary results obtained on kJ laser facilities are promising, progresses are also needed for X-ray imaging diagnostics with micrometric spatial resolution. We are therefore exploring the potentialities of LiF crystals coupled with XFEL or PW laser probes. The potentialities offered by phase-contrast imaging techniques developed on synchrotron facilities, such as Talbot-Lau X-ray deflectometry[Reference Valdivia, Stutman, Stoeckl, Mileham, Begishev, Theobald, Bromage, Regan, Klein, Muñoz-Cordovez, Vescovi, Valenzuela-Villaseca and Veloso90], should also be explored. Our team will benefit from future experimental campaigns on LULI, Orion, and OMEGA EP to improve our target design and diagnostics suite in preparation for future LMJ–PETAL experiments. The long term goal would be to diagnose extreme events and singularities in turbulent HED plasmas with
![]() $\unicode[STIX]{x03BC}\text{m}$
and ps resolutions.
$\unicode[STIX]{x03BC}\text{m}$
and ps resolutions.
Acknowledgements
This material is based upon work supported by the Agence Nationale de la Recherche under the ANR project TurboHEDP (ANR-15-CE30-0011). We would like to acknowledge the efforts of the LULI2000 operations crew, as well as the precision machining capabilities of C. Spindloe from Scitech.












