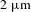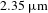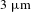1 Introduction
Laser emissions at the mid-infrared (IR) wavelength ranging from 2 to
$5~\unicode[STIX]{x03BC}\text{m}$
have been widely applied in the fields of medical surgery, spectroscopy, gas detection and security, thanks to the tremendous molecular absorption fingerprints and atmospheric transparency window located within this spectral band[Reference Jackson1–Reference Alleny6]. Most of these applications require high power and high brightness. Over the decades, researchers have developed semiconductor lasers, optical parametric oscillators and solid-state lasers to generate mid-IR lasers. In particular, the solid-state lasers based on various rare-earth (RE) dopants, including
$\text{Er}^{3+}$
,
$\text{Ho}^{3+}$
,
$\text{Dy}^{3+}$
and so on, have been widely studied[Reference Tian, Wei, Jing, Zhang and Xu7, Reference Tian, Jing, Li, Li, Li, Lei, Zhang and Xu8]. Although semiconductor lasers, gas lasers and solid-state lasers can generate mid-IR lasers over the watt level, they usually have disadvantages including poor beam brightness, low conversion efficiency and complicated configurations[Reference Ruan, Zhang, Tan, Pan, Xie, Gao and Geng9, Reference Li, Guo, Yang, Meng, Zhang, Xie, Chen, Shao, Zhang, Geng and Li10]. Recently, fibre lasers have been attracting significant interest because of their unique features such as excellent beam quality, high conversion efficiency, high surface area/volume ratio for easy heat dissipation, inherent simplicity and compactness[Reference Nilsson and Payne11–Reference Huang, Wang, Leng, Guo, Xu and Cheng13]. In addition, compared with RE-doped fibre lasers, Raman fibre lasers (RFLs) are a wavelength-agile alternative for producing gain and power within optical fibres[Reference Agrawal14]. In these, the emission wavelength is determined by the pump wavelength and Raman shift, which can be one or several cascaded Stokes orders, and is restricted by the transparency range of the fibre rather than by the spectral bands of stimulated emission. The combination of their unique optical features makes the cascaded RFLs capable for power scaling at wavelengths beyond
$2~\unicode[STIX]{x03BC}\text{m}$
.
Over the last decade, significant efforts have been made to scale the power of cascaded RFLs using typical silicate glass fibre at wavelengths between 1 and
$2~\unicode[STIX]{x03BC}\text{m}$
. To date, the maximum output power of the cascaded RFL has reached up to 300 W at 1480 nm with 65% conversion efficiency[Reference Supradeepa and Nicholson15]. Unfortunately, for the mid-IR wavelength exceeding
$2~\unicode[STIX]{x03BC}\text{m}$
, new glass materials have to be considered due to the poor transparency of silica. Further, in order to reach mid-IR wavelength, fluoride, chalcogenide or tellurite glass-based fibres act as potential candidates[Reference Jackson1]. Recently, the RFL at
$3.34~\unicode[STIX]{x03BC}\text{m}$
in the chalcogenide fibre has been demonstrated first with quasi-continuous average power of 47 mW[Reference Bernier, Fortin, Caron, El-Amraoui, Messaddeq and Vallée16]. Besides, the cascaded RFL at
$3.77~\unicode[STIX]{x03BC}\text{m}$
based on chalcogenide fibre was reported as the longest wavelength [Reference Bernier, Fortin, El-Amraoui, Messaddeq and Vallée17]. However, both the small Raman shift of 250–
$350~\text{cm}^{-1}$
and low thermal damage threshold below
$1~\text{GW}/\text{cm}^{2}$
hinder the employment of chalcogenide fibre to achieve power scaling in mid-IR[Reference Li, Chen and Chen18]. In another aspect, the RFL based on the fluoride fibre was reported with a record output power of 3.7 W at
$2.23~\unicode[STIX]{x03BC}\text{m}$
, indicating the feasibility of high power operation[Reference Fortin, Bernier, Faucher, Carrier and Vallée19]. But it is challenging to produce long wavelengths in the mid-IR region through the cascaded Raman shift, due to the relatively low Raman gain coefficient of
$0.6\times 10^{-13}~\text{m}/\text{W}$
pumped at
$1~\unicode[STIX]{x03BC}\text{m}$
[Reference Luo, Li, Li, He and Liu20].
Compared with fluoride and chalcogenide fibres, tellurite fibres offer the potential for watts-level emission at longer wavelengths than
$2.3~\unicode[STIX]{x03BC}\text{m}$
via cascaded Raman shift. The remarkable properties of tellurite fibre include the strong Raman gain coefficient and the large Raman shift, which can be up to 100 times higher than in fluorides and twice larger than in chalcogenides, respectively[Reference O’Donnell, Richardson, Stolen, Seddon, Furniss, Tikhomirov, Rivero, Ramme, Stegeman, Stegeman, Couzi and Cardinal21–Reference Thapa, Rhonehouse, Nguyen, Wiersma, Smith, Zong and Chavez-Pirson23]. Additionally, the large transparency of tellurite fibre extends far in the IR. Recently, the RFL and cascaded RFL in
$\text{TeO}_{2}$
–
$\text{Bi}_{2}\text{O}_{3}$
–ZnO–
$\text{Na}_{2}\text{O}$
(TBZN) tellurite fibre pumped by a 20 W Er-doped fluoride fibre laser (EDFFL) at
$2.8~\unicode[STIX]{x03BC}\text{m}$
have been investigated theoretically[Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24]. However, the peak Raman gain coefficient scales inversely with pump wavelength[Reference Stolen and Ippen25–Reference Mahgerefteh, Butler, Goldhar, Rosenberg and Burdge27]. Thus, the Raman gain coefficient in the case of EDFFL pumping at
$2.8~\unicode[STIX]{x03BC}\text{m}$
should be
$8.6\times 10^{-13}~\text{m}/\text{W}$
, according to the measured value of
$3.8\times 10^{-12}~\text{m}/\text{W}$
with 632.8 nm pump wavelength[Reference Mori, Masuda, Shikano and Shimizu28–Reference Qin, Jose and Ohishi30]. Moreover, the maximum power of EDFFL at the current state has been scaled up to 30 W[Reference Fortin, Bernier, Bah and Vallée31]. Based on the calculation in Section 3, the pump threshold is still above the power level in practice, even neglecting the insertion loss of fibre components and fibre connection loss.
Compared with EDFFL, the Tm-doped fibre laser (TDFL) emitting at
$2~\unicode[STIX]{x03BC}\text{m}$
can be an attractive pump source for first-order and cascaded RFL in mid-IR. The output power of TDFL has been improved to the kilowatt level allowing much higher Raman gain than EDFFL[Reference Ehrenreich, Leveille, Majid and Tankala32]. For long-wavelength generation in mid-IR, the strong Raman gain coefficient and the large Raman shift of tellurite fibre help to overcome the relatively short pump wavelength. Towards power scaling over tens of watts in mid-IR fibre laser, it is necessary to theoretically analyse the TDFL-pumped RFL and cascaded RFL based on tellurite fibres. The output performance of the third-order cascaded tellurite RFL at
$3.64~\unicode[STIX]{x03BC}\text{m}$
has been discussed numerically in Ref. [Reference Ni, Gao, Chen, Chen, Zhou, Zhang, Hu, Liao, Suzuki and Ohishi33]. The maximum output power could reach 45.2 W under 100 W pump power at
$2~\unicode[STIX]{x03BC}\text{m}$
.
In this paper, we use the finite difference method (FDM) to solve the power coupling equations with boundary conditions in the TDFL-pumped tellurite RFLs with first and cascaded Stokes orders. The model has been verified by comparing results with those in Ref. [Reference Luo, Li, Li, He and Liu20]. The influences of the fibre length and output reflectance on laser output performance are investigated, while the optimized parameters are determined for the first-order, second-order and third-order RFL, respectively.
2 Theoretical model
The material of the fibre composition determines the Raman shift and the Raman gain coefficient[Reference O’Donnell, Richardson, Stolen, Seddon, Furniss, Tikhomirov, Rivero, Ramme, Stegeman, Stegeman, Couzi and Cardinal21]. Here, we apply the tellurite fibre based on TBZN glass as the Raman gain medium, which has been investigated widely to generate tuneable RFL covering the
$\text{S}+\text{C}+\text{L}+\text{U}$
band[Reference Mori, Masuda, Shikano and Shimizu28–Reference Qin, Jose and Ohishi30, Reference Qin, Liao, Suzuki, Mori and Ohishi34]. Thanks to the current fabrication technology by the developed rod-in-tube method, the TBZN fibre shows advantages on relatively higher Raman gain coefficient and lower propagation loss than other tellurite compositions[Reference Qin, Jose and Ohishi30]. The measured Raman gain spectrum with linearly polarized pump source at 632.8 nm is shown in Figure 1
[Reference Qin, Jose and Ohishi30]. The peak Raman gain coefficient is
$3.8\times 10^{-12}~\text{m}/\text{W}$
while the corresponding Raman shift is
$740~\text{cm}^{-1}$
. Considering the peak Raman gain coefficient scales inversely with pump wavelength, the peak Raman gain coefficient is estimated to be
$1.2\times 10^{-12}~\text{m}/\text{W}$
in the case of
$2~\unicode[STIX]{x03BC}\text{m}$
pumping, while the generated first-order Stokes is
$2.35~\unicode[STIX]{x03BC}\text{m}$
[Reference Agrawal14]. Moreover, for cascaded RFL, such as second-order Stokes emitting at
$2.84~\unicode[STIX]{x03BC}\text{m}$
pumped by
$2.35~\unicode[STIX]{x03BC}\text{m}$
first-order Stokes, the peak Raman gain coefficient is estimated to be around
$1\times 10^{-12}~\text{m}/\text{W}$
.
Figure 1. Raman gain coefficient of TBZN fibre pumped at 632.8 nm [Reference Qin, Jose and Ohishi30].
Figure 2. The schematic of the all-fibrized (a) first-order and (b) cascaded RFLs. TDFL: Tm-doped fibre laser; HR: high reflectance; PR: partial reflectance.
The schematic of the all-fibrized first-order and cascaded RFLs are shown in Figures 2(a) and 2(b) separately. In general, the
$n\text{th}$
-order (
$n\geqslant 1$
) RFL is composed of the Raman fibre and
$n$
pairs of fibre Bragg gratings (FBGs) at different Stokes wavelengths on each side of the Raman fibre to resonate the intracavity Stokes fields, while an additional FBG at the pump wavelength is placed at the output end to reflect the undepleted pump into the cavity for efficient pump absorption. Except for the FBG at
$n\text{th}$
-order Stokes wavelength at the output end with partial reflectance (PR) acting as the output coupler, all the FBGs in the resonator are highly reflective (HR) to maximize the conversion efficiency. Here we only consider the single-mode fibre (SMF) in core-pumping scheme for simplicity.
Assuming that the pump power is high enough to generate
$n$
Stokes waves, we neglect the effect of spontaneous Raman scattering. We also neglect polarization effects. For simplicity, the spectral widths of pump and Stokes waves in our model are considered to be narrow enough (i.e., single frequency). Under the steady-state condition, the standard differential equations describing the evolutions of the pump and the Stokes along the
$n\text{th}$
-order RFL in both copropagating and counterpropagating directions can be written as
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}\!P_{0}^{\pm }}{\text{d}z}=\pm \left[\!-\frac{\unicode[STIX]{x1D706}}{\unicode[STIX]{x1D706}_{0}}\frac{g_{R}(\unicode[STIX]{x1D706}_{0},\unicode[STIX]{x1D706}_{1})}{A_{\text{eff}}^{0,1}}P_{0}^{\pm }(P_{1}^{+}+P_{1}^{-})-\unicode[STIX]{x1D6FC}_{0}P_{0}^{\pm }\!\!\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}\!P_{i}^{\pm }}{\text{d}z}=\frac{g_{R}(\unicode[STIX]{x1D706}_{i-1},\unicode[STIX]{x1D706}_{i})}{A_{\text{eff}}^{i-1,i}}P_{i-1}^{\pm }(P_{i-1}^{+}+P_{i-1}^{-})-\unicode[STIX]{x1D6FC}_{i}P_{i}^{\pm }\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{\unicode[STIX]{x1D706}_{i+1}}{\unicode[STIX]{x1D706}_{i}}\frac{g_{R}(\unicode[STIX]{x1D706}_{i},\unicode[STIX]{x1D706}_{i+1})}{A_{\text{eff}}^{i,i+1}}P_{i}^{\pm }(P_{i+1}^{+}+P_{i+1}^{-}),\nonumber\\ \displaystyle & & \displaystyle \qquad 1\leqslant i<n,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\text{d}\!P_{n}^{\pm }}{\text{d}z}=\pm \left[\!\frac{g_{R}(\unicode[STIX]{x1D706}_{n-1},\unicode[STIX]{x1D706}_{n})}{A_{\text{eff}}^{n-1,n}}P_{n}^{\pm }(P_{n-1}^{+}+P_{n-1}^{-})-\unicode[STIX]{x1D6FC}_{n}P_{n}^{\pm }\!\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where the superscript
$\pm$
refers to the forward- and backward-propagating pump (
$P_{0}$
) and the
$i\text{th}$
-order Stokes (
$P_{i}$
) waves;
$\unicode[STIX]{x1D706}_{0}$
,
$\unicode[STIX]{x1D706}_{i}$
are the corresponding wavelengths, and
$\unicode[STIX]{x1D6FC}_{0}$
,
$\unicode[STIX]{x1D6FC}_{j}$
their attenuation coefficients, respectively;
$g_{R}(\unicode[STIX]{x1D706}_{i-1},\unicode[STIX]{x1D706}_{i})$
is the peak Raman gain coefficient of the
$i\text{th}$
-order Stokes pumped by the
$(i-1)\text{th}$
-order Stokes; and
$A_{\text{eff}}^{i-1,i}$
is the effective mode area associated with the
$i\text{th}$
-order Stokes and its pump waves. For SMF with numerical aperture NA and core radius
$r$
, the fundamental mode field distribution can be well approximated by a Gaussian function with mode field radius
$\unicode[STIX]{x1D714}$
, which can be calculated from
$\unicode[STIX]{x1D714}=r(0.65+1.619/V^{3/2}+2.879/V^{6})$
. Here
$V$
is the normalized frequency, which is given by
$V=2\unicode[STIX]{x1D70B}rNA/\unicode[STIX]{x1D706}$
. Finally, the effective core area can be written as
$A_{\text{eff}}^{i-1,i}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D714}_{i-1}^{2}+\unicode[STIX]{x1D714}_{i}^{2})/2$
.
The differential equations at fibre front (
$z=0$
) and rear (
$z=L$
) ends satisfy the boundary condition considering insertion losses of FBGs and splicing losses of the fibres as follows:
$$\begin{eqnarray}\displaystyle P_{0}(z=0)^{+} & = & \displaystyle 10^{-0.1(n\unicode[STIX]{x1D6FF}_{F}+\unicode[STIX]{x1D6FF}_{S})}P_{in},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{0}(z=L)^{-} & = & \displaystyle 10^{-0.2\unicode[STIX]{x1D6FF}_{S}}R_{0}^{L}P_{0}(z=L)^{+},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{i}(z=0)^{+} & = & \displaystyle 10^{-0.2[(i-1)\unicode[STIX]{x1D6FF}_{F}+\unicode[STIX]{x1D6FF}_{S}]}R_{i}^{0}P_{i}(z=0)^{-},\nonumber\\ \displaystyle & & \displaystyle \quad i=1,2,\ldots ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{i}(z=L)^{-} & = & \displaystyle 10^{-0.2(i\unicode[STIX]{x1D6FF}_{F}+\unicode[STIX]{x1D6FF}_{S})}R_{i}^{L}P_{i}(z=L)^{+},\nonumber\\ \displaystyle & & \displaystyle \quad i=1,2,\ldots ,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{out} & = & \displaystyle 10^{-0.1[(n+1)\unicode[STIX]{x1D6FF}_{F}+\unicode[STIX]{x1D6FF}_{S}]}(1-R_{n}^{L})P_{n}(z=L)^{+},\end{eqnarray}$$
where
$P_{in}$
is the injected pump power, insertion losses of all FBGs and splicing losses at points A and B are supposed to
$\unicode[STIX]{x1D6FF}_{F}$
and
$\unicode[STIX]{x1D6FF}_{S}$
(in decibel), respectively,
$R_{i}$
is the reflectance of the pump (
$i=$
0) and
$i\text{th}$
-order FBG at fibre front and rear end separately, and
$P_{out}$
is the output signal power. The reflectances of the HR FBGs are assumed to be 99.5% in this paper.
Figure 3. Calculated output power versus launched pump power for fluoride RFL in Ref. [Reference Luo, Li, Li, He and Liu20]. FDM: finite difference method.
The solution of the standard differential equations with boundary conditions can be performed directly by different numerical modelling, such as shooting algorithm, Runge–Kutta algorithm, and relaxation oscillation method[Reference Li, Chen and Chen18, Reference Luo, Li, Li, He and Liu20, Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24]. However, the shooting algorithm is sensitive on the setting of initial values. Especially for cascaded RFLs, the computation becomes very cumbersome as the number of Stokes orders increases. Nevertheless, Runge–Kutta algorithm is easy to trap in local optimum leading to possible nonconvergence. Otherwise, some numerical methods such as relaxation oscillation method have to make assumptions to simplify the computation process, which may not be in accordance with the real physical process. Here we demonstrate the FDM introduced in Ref. [Reference Drainville and Das35]. The novelty of this model is considering the interaction between forward- and backward-propagating waves, which is independent on the guessed initial values and provides convergence and simplicity without the need for any approximations.
The accuracy of the numerical model has been verified by comparing the simulation results with those in Ref. [Reference Luo, Li, Li, He and Liu20], considering a single-pass fluoride RFL pumped by 1940 nm. The peak Raman gain coefficient is
$3.25\times 10^{-14}~\text{m}/\text{W}$
, while the first-order Stokes emits at 2185 nm. The fluoride Raman fibre has a core NA of 0.23 and core diameter of
$6.5~\unicode[STIX]{x03BC}\text{m}$
, whose propagation losses at pump and laser wavelengths are 0.02 and
$0.0025~\text{dB}/\text{m}$
separately. The input and output FBGs at laser wavelength with insertion losses of 0.19 dB and 0.09 dB are defined to have the reflectance of 99.95% and 95%, respectively. As shown in Figure 3, the simulation model in this paper has been confirmed by the high agreement between the two results.
3 Results and discussion
Longer pump wavelength produces higher conversion efficiency and output power, thanks to less Raman shift and shorter fibre lengths. Thus for mid-IR RFL, EDFFL emission around
$3~\unicode[STIX]{x03BC}\text{m}$
is preferred ideally. However, the maximum pump power provided by EDFFL in the current state is only about 30 W at
$2.94~\unicode[STIX]{x03BC}\text{m}$
[Reference Fortin, Bernier, Bah and Vallée31]. The corresponding peak Raman gain coefficient of the TBZN fibre at that wavelength is around
$8.2\times 10^{-13}~\text{m}/\text{W}$
. Therefore, the laser threshold of the first-order RFL pumped by
$2.94~\unicode[STIX]{x03BC}\text{m}$
can be estimated according to Equations (9) and (10)[Reference Au-Yeung and Yariv36]:
$$\begin{eqnarray}\displaystyle & \displaystyle P_{th}=\frac{2\unicode[STIX]{x1D6FC}_{1}L-\ln (R_{1}^{0}R_{1}^{L})}{2g_{R}(\unicode[STIX]{x1D706}_{0},\unicode[STIX]{x1D706}_{1})L_{\text{eff}}/A_{\text{eff}}^{0,1}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle L_{\text{eff}}=\frac{1-\exp (-\unicode[STIX]{x1D6FC}_{0}L)}{\unicode[STIX]{x1D6FC}_{0}}. & \displaystyle\end{eqnarray}$$
Here the core diameter and NA of TBZN fibre are
$8~\unicode[STIX]{x03BC}\text{m}$
and 0.15, respectively, while propagation losses at
$2.94~\unicode[STIX]{x03BC}\text{m}$
pump and
$3.76~\unicode[STIX]{x03BC}\text{m}$
first-order Stokes wavelengths are 0.2 and
$0.26~\text{dB}/\text{m}$
, respectively, according to the measured propagation loss spectrum in Ref. [Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24], which is shown in Figure 4(a). The FBG insertion and fibre splice losses are ignored. Figure 4(b) shows the calculated threshold under various fibre lengths and output reflectances. Following the results of calculations, the laser threshold takes its minimum value of 65 W with 2.3 m long fibre and 99% output reflectance. However, based on the record output power of 30 W, it remains challenging to achieve
$3{-}5~\unicode[STIX]{x03BC}\text{m}$
RFL towards ten-watt level pumped by the EDFFL. However, the TDFL at
$2~\unicode[STIX]{x03BC}\text{m}$
with high output power presents great potential as pump source for power scaling of TBZN RFL in mid-IR region. In the following sections, we will discuss the laser behaviours of the mid-IR RFL pumped by
$2~\unicode[STIX]{x03BC}\text{m}$
TDFL.
Figure 4. (a) Measured propagation loss spectrum of the TBZN fibre in Ref. [Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24]; (b) threshold power as a function of fibre length for output reflectance of 90%, 95% and 99%.
3.1 First-order Raman fibre laser
Corresponding to the
$100~\text{GW}/\text{cm}^{2}$
damage intensity threshold of TBZN fibre, the incident peak power could be 50 kW for core area of
$50~\unicode[STIX]{x03BC}\text{m}^{2}$
[Reference O’Donnell, Richardson, Stolen, Seddon, Furniss, Tikhomirov, Rivero, Ramme, Stegeman, Stegeman, Couzi and Cardinal21]. However, the exact power limit in the TBZN fibre should be quantified according to the simulated heat dissipation. We here only discuss the RFL laser performance with pump power below 300 W, which has been demonstrated in our group[Reference Wang, Jin, Wu, Zhou, Wang, Xiao and Liu37]. The peak Raman gain coefficient and first-order Stokes emission wavelength are calculated to be
$1.2\times 10^{-12}~\text{m}/\text{W}$
and
$2.35~\unicode[STIX]{x03BC}\text{m}$
, respectively. As shown in Figure 4(a), the propagation losses at pump and signal wavelengths are 0.3 and
$0.33~\text{dB}/\text{m}$
separately[Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24]. The TBZN Raman fibre has the core diameter of
$8~\unicode[STIX]{x03BC}\text{m}$
and NA of 0.15. For accuracy, it is necessary to consider the FBG insertion and fibre splice losses. According to the previous demonstration on TBZN RFL at around
$1.5~\unicode[STIX]{x03BC}\text{m}$
, we define the silica and TBZN fibre splice loss to be 0.3 dB[Reference Ebendorff-Heidepriem, Kuan, Oermann, Knight and Monro22]. The insertion loss of FBG is assumed to be 0.2 dB, which might be varied in experiment.
Figure 5(a) shows the output power of the first-order RFL as a function of output reflectance for different fibre lengths. For 0.3 and 0.5 m long fibres, the maximum output powers are about 125 and 145 W referring to the optimum output reflectance of 40% and 25% separately. For fibre lengths longer than 1 m, the optimum output reflectance is 5%, which is also confirmed in Figure 5(b), leading to the output power of 160 W and 157 W for 1 m and 2 m fibres, respectively. For relatively short fibre, the growth of the output power is observed as the output reflectance increases before reaching its optimum. Once the output reflectance increases beyond the optimum, the output power starts to decrease sharply. For a certain fibre length, as the output reflectivity increases, the feedbacked signal power in the backward direction keeps increasing, while the transmission decreases. For output reflectivity beyond the optimum, the backward signal power is high enough leading to the saturated signal power in the forward direction. In that case, the output power degrades sharply as a result of the dual role of the saturated forward signal power and decreased transmission. Moreover, the fibre length also affects the optimum output reflectance and the corresponding maximum output power as a result of the interaction between the overall Raman gain and fibre loss.
Furthermore, the dependence of the output power on the fibre length for different output reflectance is shown in Figure 5(b). The maximum output of 162 W is observed with 1.3 m fibre length and 5% output reflectance. As the fibre length increases, it can be seen that the output power rises sharply to its maximum and then declines slowly owing to the increased propagation loss and sufficient pump depletion. Besides, the optimum output reflectance becomes lower with longer fibre length, while the optimum fibre length becomes longer with lower output reflectance. This is related to the fact that higher Raman gain through longer fibre length is required when the cavity feedback is lower.
Figure 5. Output power of the first-order RFL as a function of (a) output reflectance for fibre length of 0.3 m, 0.5 m, 1 m, 2 m, and (b) fibre length for output reflectance of 5%, 10%, 15% and 20%.
Figure 6. (a) Power distribution along the fibre length in first-order RFL pumped by TDFL; (b) output power of first-order Stokes versus pump power.
Figure 6(a) shows the power evolution in RFL with the optimized fibre length of 1.3 m and output reflectance of 5%. The pump power is depleted entirely through the long fibre and double-pass cavity. In addition, the first-order Stokes waves in both forward and backward directions keep amplifying, indicating an unsaturated state. The conversion efficiency from the pump power to output power is about 54%, while the quantum defect is about 14.9%. Figure 6(b) presents the output power against the pump power with the optimized cavity parameters, compared with the results with 0.5 m fibre length or 10% output reflectance. With the same output reflectance of 5%, the slope efficiencies are 71% and greater than 95% for 1.3 m and 0.5 m long fibres separately. The fact that the shorter fibre length contributes to higher slope efficiency should be explained by the lower propagation loss. With the same fibre length of 1.3 m, the slope efficiencies are 71% and 66% for 5% and 10% output reflectance, respectively, which can be explained by the fact that lower feedback leads to higher Raman gain.
Figure 7. Power evolution of (a) pump, (b) first-order Stokes, (c) second-order Stokes waves in second-order RFL pumped by TDFL.
Figure 8. Output power of second-order RFL as a function of (a) output reflectance for fibre length of 0.5 m, 1 m, 2 m and 3.1 m, (b) fibre length for output reflectance of 5%, 10%, 15% and 20%.
3.2 Second-order Raman fibre laser
To achieve longer signal wavelength, one could apply the cascaded RFL with multi-order Stokes generation. In the case of TDFL pumping, the second-order Stokes emits at
$2.84~\unicode[STIX]{x03BC}\text{m}$
considering
$740~\text{cm}^{-1}$
Raman shift from
$2.35~\unicode[STIX]{x03BC}\text{m}$
first-order Stokes. Note that the second-order Raman gain coefficient becomes
$1\times 10^{-12}~\text{m}/\text{W}$
due to longer pump wavelength. On the basis of first-order RFL, the second-order RFL cavity adds the
$2.84~\unicode[STIX]{x03BC}\text{m}$
HR and PR FBGs at input and output ends, respectively, while the PR FBG at
$2.35~\unicode[STIX]{x03BC}\text{m}$
is replaced by HR FBG. Here, we define the fibre parameters and HR FBG reflectance as before. As shown in Figure 4(a), the background loss at
$2.84~\unicode[STIX]{x03BC}\text{m}$
is
$0.24~\text{dB}/\text{m}$
[Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24]. The fibre splice and FBG insertion losses are still 0.3 dB and 0.2 dB, respectively.
Figure 7 shows the longitudinal power distributions of each wave in the second-order RFL with 3.1 m long fibre length and 5% output reflectance. The pump wave has been almost completely converted into first-order Stokes wave through the forward single pass. As the pump of second-order Stokes, the forward first-order Stokes experiences amplification and depletion before and after the 1.2 m fibre position, respectively, while the backward first-order Stokes wave performs the opposite trend with the same turning position. The second-order Stokes in both directions is still below saturation and is amplified during the whole RFL.
In order to find how the output reflectance and fibre length affect the laser characteristics, we illustrate the relationship between the output power of second-order RFL and the output reflectance in Figure 8(a) and fibre length in Figure 8(b). As shown in Figure 8(a), the maximum output powers for 0.5 m, 1 m, 2 m, and 3.1 m long fibres can be up to 67 W, 83 W, 91 W and 92 W, with respect to output reflectance of 30%, 15%, 10% and 5% separately. The optimized output reflectance is lower for longer fibre length until the optimum fibre length. As shown in Figure 8(b), for 5%, 10%, 15% and 20% output reflectance, the obtainable output power is as high as 92 W, 91 W, 89 W and 87 W, respectively, while the optimal fibre length is 3.1 m, 2.4 m, 2.1 m and 1.9 m separately. The maximum output power declines a little as output reflectance increases, which is similar to the first-order RFL. Even so, the maximum output power under the optimal fibre length and output reflectance varies only slightly. Comparing Figures 8(a) and 8(b), the output power is sensitive to output reflectance within its whole range, while the tolerance on the fibre length is low only for fibre length shorter than 1.5 m.
Not only the output power, but also the slope efficiency and threshold should be considered for cavity optimization. Figure 9 presents the second-order output power versus the pump power with the fibre length of 1.9 m and 3.1 m, output reflectance of 5% and 20% separately. The conversion efficiency at maximum output power and slope efficiency with 3.1 m fibre length and 5% output reflectance are around 31% and 41% separately. For 1.9 m long fibre, the slope efficiency is 42% and 36% with respect to 5% and 20% output reflectance , respectively. Although short fibre length enables a slight increment in slope efficiency under the same output reflectance, it would lead to high threshold. Besides, in comparison with first-order RFL, the slope efficiency with optimized cavity parameters drops from 71% to 41%, which can be explained by the much larger quantum defect, higher insertion loss and propagation loss due to more FBGs and longer fibre length.
Figure 9. Output power of second-order RFL under different pump powers.
3.3 Third-order Raman fibre laser
For mid-IR laser beyond
$3~\unicode[STIX]{x03BC}\text{m}$
, it is attractive to apply the third-order RFL lasing at
$3.6~\unicode[STIX]{x03BC}\text{m}$
, thanks to the uniform heat dissipation along the relatively long fibre. Here we simulate the third-order RFL with the same TBZN fibre as the subsections above, while the propagation loss at
$3.6~\unicode[STIX]{x03BC}\text{m}$
is set to
$0.2~\text{dB}/\text{m}$
[Reference Zhu, Geng, Zhu, Li, Chen, Norwood, Manzur and Peyghambarian24]. The Raman gain coefficient pumped by
$2.84~\unicode[STIX]{x03BC}\text{m}$
second-order Stokes is estimated to be
$0.84\times 10^{-12}~\text{m}/\text{W}$
. Except for the output FBG for last-order Stokes, all the FBGs in the cavity are HR with 99.5% reflectance. The fibre length and reflectance of output FBG are the variables to be optimized. The intracavity power distribution of each wave along the 5.5 m fibre with 45% output reflectance is shown in Figure 10.
Figure 10. Longitudinal power evolution of (a) pump, (b) first-order Stokes, (c) second-order Stokes, (d) third-order Stokes in third-order RFL pumped by TDFL.
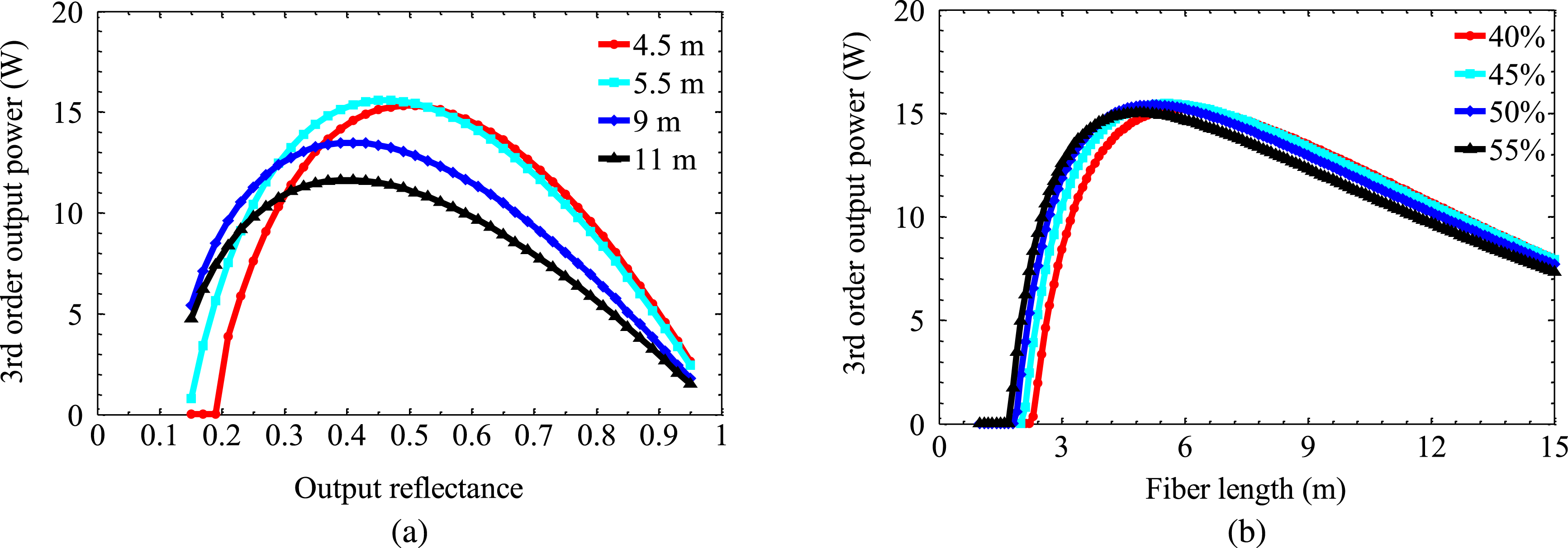
Figure 11. Output power of third-order RFL as a function of (a) output reflectance for fibre length of 4.5 m, 5.5 m, 9 m and 11 m, (b) fibre length for output reflectance of 40%, 45%, 50% and 55%.
The variations in output power of the generated third-order Stokes with output reflectance for fibre length of 4.5 m, 5.5 m, 9 m and 11 m are shown in Figure 11(a). The optimum reflectance is 49%, 45%, 41% and 41%, resulting in the maximum output power of 15 W, 16 W, 13 W and 12 W separately. The dependence of output power on fibre length for output reflectance of 40%, 45%, 50% and 55% is shown in Figure 11(b). For all output reflectance, the maximum output power ranges from 15 W to 16 W with the optimum fibre length of 5.8 m, 5.5 m, 5.2 m and 4.9 m separately.
As shown in Figure 12, the conversion efficiency at the highest pump power and slope efficiency are about 5% and 16% when the fibre length and output reflectance are optimized to 5.5 m and 45% separately. The slope efficiency with the output reflectance of 55% is 14% and 13% for fibre length of 4.9 m and 5.5 m, respectively. The output power and slope efficiency can be further improved by reducing the losses of the tellurite fibre and FBG component. Moreover, power scaling towards longer wavelength in mid-IR region can also be expected by developing the fabrication technology of tellurite fibre and its components in the near future.
Figure 12. Output power of third-order RFL as a function of pump power.
4 Conclusion
In this paper, we have demonstrated the numerical simulations on the
$2~\unicode[STIX]{x03BC}\text{m}$
TDFL-pumped tellurite RFLs emitting in the mid-IR region for the first time. Although the EDFFL contributes to less fibre component and shorter fibre length, thanks to the long pump wavelength, the maximum pump power is still below the threshold of the tellurite RFLs. As a candidate to pump the mid-IR RFLs, the TDFL has presented significant potential on power scaling over hundreds of watts within the spectral range of 2–
$3~\unicode[STIX]{x03BC}\text{m}$
and tens of watts beyond
$3~\unicode[STIX]{x03BC}\text{m}$
, respectively. In the case of TDFL pumping, the first-order and cascaded RFLs with second and third-order Stokes generations based on TBZN fibre have been analysed and optimized, indicating strong dependence of the output power on both the fibre length and output reflectance. The optimum fibre length and output reflectance are found to be 1.3 m and 5% for first-order RFL separately, leading to the highest output power of 162 W. For cascaded RFL emitting at
$2.85~\unicode[STIX]{x03BC}\text{m}$
, the fibre length and output reflectance are optimized to be 3.1 m and 5%, respectively, ensuring the maximum output power of 92 W. The highest output power of the third-order cascaded RFL at
$3.6~\unicode[STIX]{x03BC}\text{m}$
is obtained to be 16 W with fibre length of 5.5 m and output reflectance of 45%. Except for the fibre length and output reflectance, both the fibre propagation loss and FBG insertion loss would determine the laser performance. In order to achieve further power scaling, more efforts should be made for developing techniques of fibre fabrication and FBG writing to minimize the insertion loss, which are also necessary for wavelength extension beyond
$4~\unicode[STIX]{x03BC}\text{m}$
.
Acknowledgements
The authors acknowledge help from the China Postdoctoral Science Foundation (No. 2016M603003) and State Key Laboratory of Luminescent Materials and Devices from South China University of Technology (No. 2017-skllmd-09).
Open access
