1 Introduction
The Shenguang-II (SG-II) laser driver is used in operation for inertial confinement fusion (ICF) experiments. Due to the increase in laser energy and the expansions of the laser driver’s scale, the cleanliness of the working environment with numerous optical elements has greatly affected the construction cycle and operating life of the high power solid-state laser driver[Reference Yin, Zhuang and Zhang1–Reference Yang, Liu and Ren4]. Recent studies have shown that flashlamp illumination is a major factor causing damage to the lasing media (slab or disk) when the contaminant particles deposit onto the surface of the optical element in a multi-segment Nd:glass disk laser amplifier[Reference He, Kang, Zhang, Chen, Ding, Yin and Hu5–Reference Cheng, Miao, Wang, Qin, Ye, He, Ma, Zhao and He8]. Because the full fluence of the flashlamp illumination in SG-II can reach
![]() $10~\text{J}/\text{cm}^{2}$
, most contaminant particles on the surface of the lasing media will be melted or decomposed. This will produce a local thermal gradient and thermal shock on the surface of the lasing media, and subsequently lead to crazing in the Nd:glass disk[Reference Gourdin and Monticelli9–Reference Guéhenneux, Bouchut, Veillerot, Pereira and Tovena13]. The cleanliness of the multi-segment Nd:glass disk amplifier is related to the operational efficiency of the laser driver and service life of the Nd:glass disk. Researchers are greatly focusing on the production and deposition behavior of the contaminant particles, the procedure for cleaning optical elements, and cleanliness requirements of the work environment[Reference Norton, Honig, Rubenchik, Rigatti, Stolz and Matthews14–Reference Stahl19]. Cleanliness requirements are strictly imposed during assembly, cassette transfer, and amplifier operations in high power laser driver systems such as SG-II, SG-III, and the National Ignition Facility (NIF). In order to improve cleanliness of mechanical and optical components before assembly, we determine quantification control of the surface cleanliness. After flashlamp illumination, the residence time of aerosol particles is shortened and the cleanliness level of the amplifier is increased to a certain extent by blowing clean nitrogen into the amplifiers. However, studies on the particle–nitrogen (solid–gas) coupled mode and optimization of the flow field in the main amplifier are rare.
$10~\text{J}/\text{cm}^{2}$
, most contaminant particles on the surface of the lasing media will be melted or decomposed. This will produce a local thermal gradient and thermal shock on the surface of the lasing media, and subsequently lead to crazing in the Nd:glass disk[Reference Gourdin and Monticelli9–Reference Guéhenneux, Bouchut, Veillerot, Pereira and Tovena13]. The cleanliness of the multi-segment Nd:glass disk amplifier is related to the operational efficiency of the laser driver and service life of the Nd:glass disk. Researchers are greatly focusing on the production and deposition behavior of the contaminant particles, the procedure for cleaning optical elements, and cleanliness requirements of the work environment[Reference Norton, Honig, Rubenchik, Rigatti, Stolz and Matthews14–Reference Stahl19]. Cleanliness requirements are strictly imposed during assembly, cassette transfer, and amplifier operations in high power laser driver systems such as SG-II, SG-III, and the National Ignition Facility (NIF). In order to improve cleanliness of mechanical and optical components before assembly, we determine quantification control of the surface cleanliness. After flashlamp illumination, the residence time of aerosol particles is shortened and the cleanliness level of the amplifier is increased to a certain extent by blowing clean nitrogen into the amplifiers. However, studies on the particle–nitrogen (solid–gas) coupled mode and optimization of the flow field in the main amplifier are rare.
In this paper, we focused on the need for cleanliness requirements of the amplifiers with vector flow-field optimization. First, we established the gas–solid three-dimensional (3D) numerical model based on the 130-disk amplifier. Second, we conducted the flow visualization experiment and particle count experiment to verify the numerical model. Finally, we optimized the structural type for the input and output of the multi-segment disk amplifier, and the vector flow is considered to improve the cleanliness of the multi-segment disk amplifier.
2 Numerical simulation model and validity experiments
2.1 Computational model
Half of the amplifier symmetrical structure is analyzed because of the symmetry of the multi-segment disk amplifier itself. The computational model includes the inlet, the cavity, the Nd:glass slab, and the outlet. In the computational process, we carry out the procedure based on the following assumptions: (1) the thermal characteristics of the fluid are steady; (2) the flow state of the fluid depends on the Reynolds number when the inlet velocity is determined; and (3) the aerosol particles in the inner cavity of the amplifier are small in diameter, light in weight, and adequate in the follow-up property with the clean gas. Therefore, the flow field can represent the distribution of aerosol particles. The computational equations include the continuity equation
and the momentum equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}(u_{i}u_{j})}{\unicode[STIX]{x2202}x_{j}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70C}F-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}\left[\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\right)\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x2202}(u_{i}u_{j})}{\unicode[STIX]{x2202}x_{j}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70C}F-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}\left[\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\right)\right],\end{eqnarray}$$
where
![]() $u$
,
$u$
,
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $F$
,
$F$
,
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $p$
are the velocity vector, density, force, dynamic viscosity and pressure, respectively.
$p$
are the velocity vector, density, force, dynamic viscosity and pressure, respectively.
There are five total unknown variables:
![]() $u$
,
$u$
,
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $F$
,
$F$
,
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $p$
, while the number of equations is only two. Therefore, the instantaneous flow is the decomposition of two parts with an average and fluctuating value which is based on the Reynolds time-averaged equations (RANS equations). Thus,
$p$
, while the number of equations is only two. Therefore, the instantaneous flow is the decomposition of two parts with an average and fluctuating value which is based on the Reynolds time-averaged equations (RANS equations). Thus,
where
![]() $\overline{u_{i}}$
and
$\overline{u_{i}}$
and
![]() $u_{i}^{\prime }$
are average velocity and fluctuating velocity (
$u_{i}^{\prime }$
are average velocity and fluctuating velocity (
![]() $i=1,2,3$
), respectively.
$i=1,2,3$
), respectively.
The 3D generalized model is shown as
and
where
![]() $\unicode[STIX]{x1D707}_{t}$
is the eddy diffusivity.
$\unicode[STIX]{x1D707}_{t}$
is the eddy diffusivity.
We substitute equations (3), (4), and (5) in equations (1) and (2) to produce the equations
and
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}u_{i}}{\text{D}t} & = & \displaystyle -\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left[\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{i}}-\frac{2}{3}\unicode[STIX]{x1D6FF}_{ij}\frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{l}}\right)\right]+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}(-\unicode[STIX]{x1D70C}\overline{u_{i}^{\prime }u_{j}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}u_{i}}{\text{D}t} & = & \displaystyle -\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x_{i}}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}\left[\unicode[STIX]{x1D707}\left(\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.\frac{\unicode[STIX]{x2202}u_{j}}{\unicode[STIX]{x2202}x_{i}}-\frac{2}{3}\unicode[STIX]{x1D6FF}_{ij}\frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{l}}\right)\right]+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{j}}(-\unicode[STIX]{x1D70C}\overline{u_{i}^{\prime }u_{j}^{\prime }}).\end{eqnarray}$$
Based on the
![]() $k\text{-}\unicode[STIX]{x1D700}$
model, the average velocity gradient is proportional to Reynolds stress, where
$k\text{-}\unicode[STIX]{x1D700}$
model, the average velocity gradient is proportional to Reynolds stress, where
The turbulent kinetic energy
![]() $k$
equation and the dissipation rate
$k$
equation and the dissipation rate
![]() $\unicode[STIX]{x1D700}$
equation in the standard
$\unicode[STIX]{x1D700}$
equation in the standard
![]() $k\text{-}\unicode[STIX]{x1D700}$
model are as follows:
$k\text{-}\unicode[STIX]{x1D700}$
model are as follows:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}k}{\text{D}t} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}\left[\left(\unicode[STIX]{x1D707}+\frac{\unicode[STIX]{x1D707}_{t}}{\unicode[STIX]{x1D70E}_{k}}\right)\frac{\unicode[STIX]{x2202}k}{\unicode[STIX]{x2202}x_{i}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,G_{k}+G_{b}-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}-Y_{M}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}k}{\text{D}t} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}\left[\left(\unicode[STIX]{x1D707}+\frac{\unicode[STIX]{x1D707}_{t}}{\unicode[STIX]{x1D70E}_{k}}\right)\frac{\unicode[STIX]{x2202}k}{\unicode[STIX]{x2202}x_{i}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,G_{k}+G_{b}-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D700}-Y_{M}\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}\unicode[STIX]{x1D700}}{\text{D}t} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}\left[\left(\unicode[STIX]{x1D707}+\frac{\unicode[STIX]{x1D707}_{t}}{\unicode[STIX]{x1D70E}_{k}}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}}{\unicode[STIX]{x2202}x_{i}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,C_{1\unicode[STIX]{x1D700}}\frac{\unicode[STIX]{x1D700}}{k}(G_{k}+C_{3\unicode[STIX]{x1D700}}G_{b})-C_{2\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x1D700}^{2}}{k},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}\frac{\text{D}\unicode[STIX]{x1D700}}{\text{D}t} & = & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{i}}\left[\left(\unicode[STIX]{x1D707}+\frac{\unicode[STIX]{x1D707}_{t}}{\unicode[STIX]{x1D70E}_{k}}\right)\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}}{\unicode[STIX]{x2202}x_{i}}\right]\nonumber\\ \displaystyle & & \displaystyle +\,C_{1\unicode[STIX]{x1D700}}\frac{\unicode[STIX]{x1D700}}{k}(G_{k}+C_{3\unicode[STIX]{x1D700}}G_{b})-C_{2\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}\frac{\unicode[STIX]{x1D700}^{2}}{k},\end{eqnarray}$$
where
![]() $G_{k}$
,
$G_{k}$
,
![]() $G_{b}$
,
$G_{b}$
,
![]() $Y_{M}$
and
$Y_{M}$
and
![]() $\unicode[STIX]{x1D707}_{t}$
are turbulent kinetic energy caused by the mean velocity gradient, turbulent kinetic energy caused by buoyancy, total dissipation rate caused by the turbulent expansion of compressible velocity, and the turbulence coefficient, respectively.
$\unicode[STIX]{x1D707}_{t}$
are turbulent kinetic energy caused by the mean velocity gradient, turbulent kinetic energy caused by buoyancy, total dissipation rate caused by the turbulent expansion of compressible velocity, and the turbulence coefficient, respectively.
If the flow state of the model is assumed to be completely turbulent, the effects of molecular viscosity can be neglected. The standard
![]() $k\text{-}\unicode[STIX]{x1D700}$
model can be used to solve the turbulent kinetic energy and its dissipation rate equation.
$k\text{-}\unicode[STIX]{x1D700}$
model can be used to solve the turbulent kinetic energy and its dissipation rate equation.
The experiment to validate the numerical model was carried out. We adopted a tetrahedral unstructured grid, and the grids of the inlet, outlet and Nd:glass were meshed into much finer grids to meet the requirement of the wall function method. Grid independence tests were performed to obtain a nearly grid-independent solution. In these tests, three different grid systems, with 148,639, 357,564 and 1,256,856 cells, were adopted for the calculation of the entire simulation model. The difference in the overall pressure loss and the average heat transfer coefficient between the last two grid systems was approximately 1.5%. The governing equations were discretized using the finite volume method. The coupling between velocity and pressure was carried out using the SIMPLE algorithm. The convergence criterion of the mass residual and the energy residual should be less than
![]() $10^{-6}$
and less than
$10^{-6}$
and less than
![]() $10^{-8}$
, respectively.
$10^{-8}$
, respectively.
2.2 Validity experiment for the flow field of the simulation model
There are many factors that affect the flow field in the multi-segment disk amplifier. In order to verify the simulation results with the standard
![]() $k\text{-}\unicode[STIX]{x1D700}$
model, the airflow smoke experiment on the 130-disk amplifier was carried out. The configuration of the 130-disk amplifier is as shown in Figure 1. The amplifier structure was in accordance with the computational geometry model; because Nd:glass is expensive to manufacture, we replaced Nd:glass with black rubber with the same size, as black rubber as a background is better for observing the flow field of smoke. Smoke was generated by a 400 W smoke generator with a smoke yield of
$k\text{-}\unicode[STIX]{x1D700}$
model, the airflow smoke experiment on the 130-disk amplifier was carried out. The configuration of the 130-disk amplifier is as shown in Figure 1. The amplifier structure was in accordance with the computational geometry model; because Nd:glass is expensive to manufacture, we replaced Nd:glass with black rubber with the same size, as black rubber as a background is better for observing the flow field of smoke. Smoke was generated by a 400 W smoke generator with a smoke yield of
![]() $300~\text{ft}^{3}/\text{min}$
. In order to achieve the desired inlet pressure, the smoke generator was placed in a sealed chamber, which was equipped with a 1100 W air pump for the inlet.
$300~\text{ft}^{3}/\text{min}$
. In order to achieve the desired inlet pressure, the smoke generator was placed in a sealed chamber, which was equipped with a 1100 W air pump for the inlet.

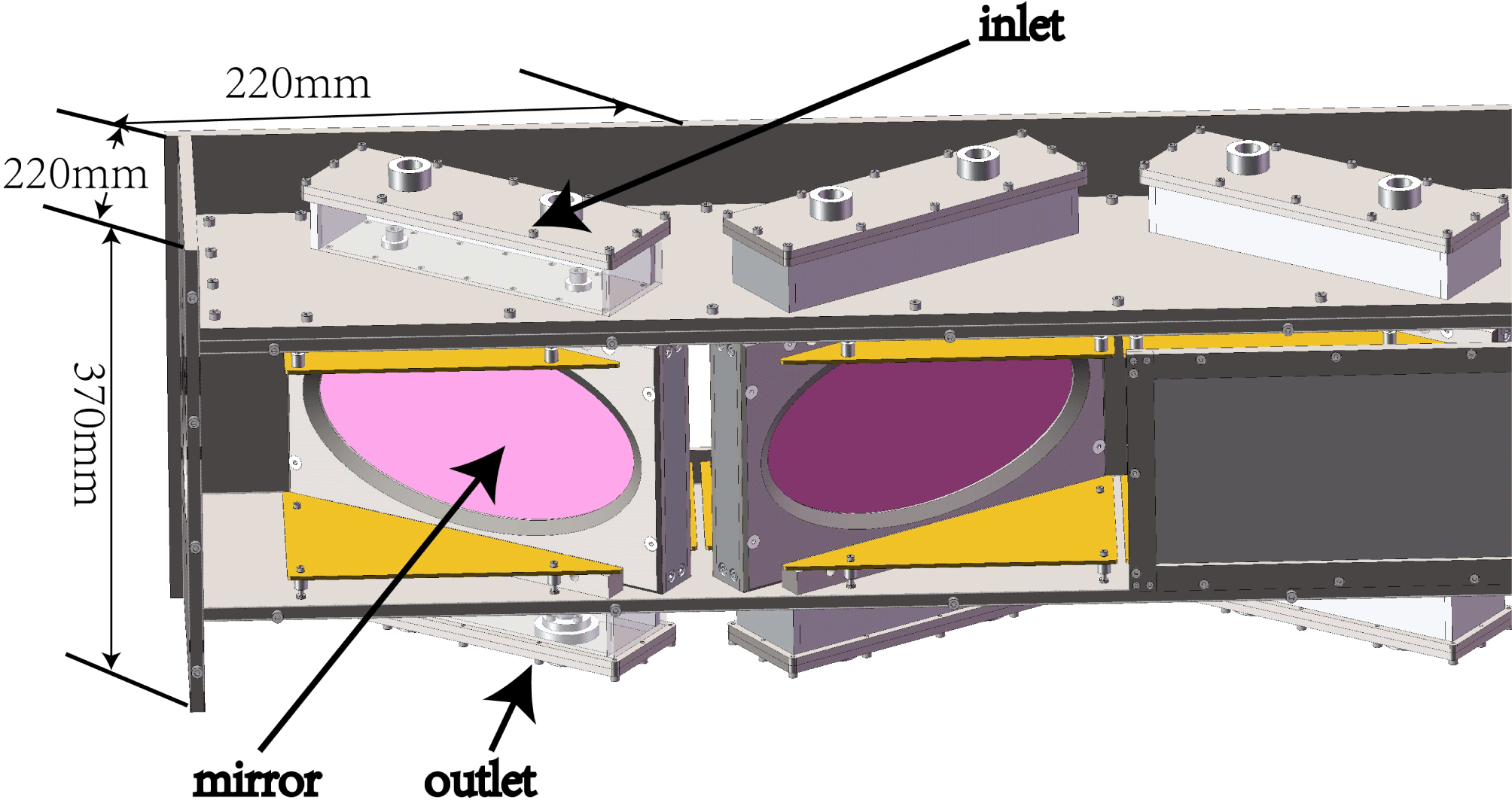
Figure 1. The configuration of the 130-disk amplifier.

Figure 2. Flow field of the cavity of the 130-disk amplifier: (a) numerical simulation result; (b) experimental result.
Figure 2 shows the clean gas flow field through the inlet into the cavity of the disk amplifier. The airflow direction is along the axis of the inlet near the inlet area, but the airflow diffusion takes place below the middle of the amplifier cavity. At the same time, most of the airflow which cannot be exhausted from outlet is blocked. The blocked airflow returns to the cavity of the amplifier and introduces obvious eddy in the cavity of the amplifier. The flow field of the cavity of the 130-disk amplifier reaches stable state after 7 seconds, and there is eddy in the cavity of 130-disk amplifier obviously.
The clean gas inside the cavity at the lower part of the amplifier obviously causes turbulence. The numerical simulation results are in good agreement with the experimental results, which indicates that the model adopted in the numerical simulation is credible.
2.3 Validity experiment for the contaminant particle deposition model
The cleanliness level of the cavity of the amplifier is defined by Federal Standard 209 and is given by
where
![]() $x$
and
$x$
and
![]() $f_{\text{vol}}(x)$
are the diameter of the contaminant particle in
$f_{\text{vol}}(x)$
are the diameter of the contaminant particle in
![]() $\unicode[STIX]{x03BC}\text{m}$
and the number of contaminant particles per cubic foot greater than
$\unicode[STIX]{x03BC}\text{m}$
and the number of contaminant particles per cubic foot greater than
![]() $x$
in diameter, respectively.
$x$
in diameter, respectively.
The gas–solid coupling multiphase flow model makes the following assumptions. (1) Most of the contaminant particles are produced by flashlamp high irradiation that pyrolyzes materials within the slab cavity and thus produces large quantity of airborne particles at the scale of micrometers. (2) The particle size of contaminant particles is set to be
![]() $0.3~\unicode[STIX]{x03BC}\text{m}$
because the particle size of contaminant is the dominant size among the size of contaminant dependent on experimental results[Reference Gourdin and Monticelli9, Reference Honig10]. (3) The concentration of contaminant particles in the clean gas is only studied for 20 minutes. (4) With regard to the structure of the inlet, outlet and cavity of the amplifier, pressure and clean gas, they are the same as those of the 130-disk amplifiers currently in operation. (5) The time duration of blowing clean gas is 20 minutes, which is the same as the experimental test time duration.
$0.3~\unicode[STIX]{x03BC}\text{m}$
because the particle size of contaminant is the dominant size among the size of contaminant dependent on experimental results[Reference Gourdin and Monticelli9, Reference Honig10]. (3) The concentration of contaminant particles in the clean gas is only studied for 20 minutes. (4) With regard to the structure of the inlet, outlet and cavity of the amplifier, pressure and clean gas, they are the same as those of the 130-disk amplifiers currently in operation. (5) The time duration of blowing clean gas is 20 minutes, which is the same as the experimental test time duration.
This experiment monitors the cleanliness of the amplifier near the outlet with the airborne particle counter (model series: Y09-4).
Figure 3 shows that the cleanliness of the 130-disk amplifier reaches cleanliness level of class 100 within 5 minutes; thus, the cleanliness level can meet our requirement. The numerical results of the gas–solid coupling model are in good agreement with the experimental results.

Figure 3. Concentration change of contaminant particles with time in the 130-disk amplifier.
3 Result and discussion
Studies are conducted to improve the flow field of the amplifier in two aspects. On the one hand, the structure and number of inlets and outlets are developed to eliminate the vortex area on the surface of Nd:glass and in the cavity of the amplifier. On the other hand, the configuration of inlets and outlets for the amplifier is improved so that the clean gas flows as vector flows can efficiently exhaust contaminant particles. More importantly, the cleanliness level of the multi-segment amplifier reaches the requirement with class 100 within 5 minutes under nitrogen purge. Stopping clean gas purge after 20 minutes, the cleanliness level deteriorates to class 1000. Even if the clean gas purge time is extended to 30 minutes, the cleanliness level still deteriorates to class 1000 based on the experimental result[Reference Yang, Liu and Ren4, Reference Manes, Spaeth, Adams and Bowers11]. The deterioration of cleanliness level in the multi-segment amplifier happens mainly because of the existence of eddy in the flow field. The contaminant particles cannot be purged but follows the eddy of clean gas in the cavity of the multi-segment amplifier. Therefore, it is important to improve the flow field of the cavity of the multi-segment amplifier for the improvement of cleanliness level.
The vector flow direction is not just a single direction, and can flow in any direction. The dilution purification mechanism is not only different from the dilution-mixing effects with non-unidirectional cleaning technology, but also from the parallel streamline piston effect with unidirectional flow. Although the streamlines of the vector flow are not parallel, they do not cross. Even though vector flow does not depend on the mixing effect, it still relies on the oblique flow to discharge clean gas and contaminant particles. Therefore, vector flow can achieve a higher level of cleanliness for the amplifier.
3.1 Flow field of the current multi-segment disk amplifier

Figure 4. Current configuration of inlets and outlets for the multi-segment disk amplifier. (a) Configuration of the multi-segment disk amplifier. (b) Simulation model of the multi-segment disk amplifier.

Figure 5. Flow field of the current multi-segment disk amplifier: (a) velocity distribution in the cavity; (b) streamline in the cavity; (c) velocity distribution on the surface of Nd:glass; (d) streamline on the surface of Nd:glass.
The configuration of the multi-segment disk amplifier is as shown in Figure 4. It includes inlet, cavity, mirror and outlet. Figure 5 shows the flow field of the cavity of the multi-segment amplifier and surface of Nd:glass. Under the present configuration of inlets and outlets, there is an obvious vortex not only in the middle of the cavity of the amplifier, but also on the surface of the Nd:glass even though the velocity of the clean gas reaches the maximum in the flow field at the inlet and outlet positions. The existence of eddy flow may not only lead to the retention of contaminant particles, but also the deposition of contaminant particles on the surface of Nd:glass. Consequently, the probability of damage to optical components is greatly increased. It is necessary to develop the configuration of inlets and outlets and obtain vector flow for the cleanliness level of the amplifier.
3.2 Optimized flow field of the multi-segment disk amplifier based on vector flow
In order to more effectively achieve coupling for the structure of the inlet and outlet of the amplifier, we developed the configuration of inlets and outlets to achieve vector flow of the clean gas. The inlets of the clean gas are inlet 1, inlet 2 and inlet 3. Inlet 1 and inlet 2, which are near the wall of the amplifier, are fan-shaped, to obtain vector flow in the cavity of the amplifier. Inlet 3, which is near the Nd:glass, is rectangular-shaped to achieve vector flow on the surface of Nd:glass. The fan-shaped outlet is near the Nd:glass, and the fan-shaped opening corresponds to the inlet. The results of the flow field for the optimized amplifier can be shown in Figure 6.

Figure 6. Optimized configuration of inlets and outlets of the amplifier.

Figure 7. Flow field of the multi-segment disk amplifier with the vector flow scheme: (a) velocity distribution in the cavity; (b) streamline in the cavity; (c) velocity distribution on the surface of Nd:glass; (d) streamline on the surface of Nd:glass.
Figure 7 shows that we obtained vector flow for the flow field of the cavity of the amplifier and on the surface of the Nd:glass. The velocity of the inlet, which is optimized, decreased to
![]() $1/3$
of that of the current nozzle inlet with the same flow rate. However, based on the optimized construction of inlets and outlets, the vector flow oblique push mode for clean gas can be realized, and there is no obvious vortex flow in the flow field of the cavity of the amplifier and on the surface of the Nd:glass. Consequently, contaminant particles are uniformly discharged with the vector flow of clean gas.
$1/3$
of that of the current nozzle inlet with the same flow rate. However, based on the optimized construction of inlets and outlets, the vector flow oblique push mode for clean gas can be realized, and there is no obvious vortex flow in the flow field of the cavity of the amplifier and on the surface of the Nd:glass. Consequently, contaminant particles are uniformly discharged with the vector flow of clean gas.
4 Conclusion
Based on the validity experiments for the flow field of the 130-disk amplifier and the deposition of contaminant particles in the 130-disk amplifier, we obtain a valid three-dimensional two-phase flow numerical simulation model. We analyzed the disadvantages of the current flow field of the multi-segment disk amplifier. Subsequently, we studied the flow field of vector flow for the multi-segment disk amplifier with optimized inlets and outlets. The results demonstrate that we can effectively achieve better cleanliness levels with the vector flow scheme.
Acknowledgement
This project is supported by the National Natural Science Foundation of China (Grant No. 61505228).