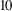2 Experimental setup

The experiment was undertaken at the petawatt arm of the Vulcan laser system at the Rutherford Appleton Laboratory, UK. The laser pulses, at a central wavelength of 1.054 μm, temporal duration of 800 ± 200 fs and energy of 280 ± 45 J, were focused with an f/3 off-axis parabola into spots approximately 5 μm in diameter FWHM (full width at half maximum). This resulted in on-target intensities of approximately $\left(3-5\right)\times {10}^{20}$ W/cm². The pulses were incident on 10 μm thick gold foil targets, which were attached to HCs via a delay line as in the work of Ahmed et al. ^[ Reference Ahmed, Hadjisolomou, Naughton, Alejo, Brauckmann, Cantono, Ferguson, Cerchez, Doria, Green, Gwynne, Hodge, Kumar, Macchi, Prasad, Willi, Borghesi and Kar ^{17 ]}. The HCs implemented were all made of 125 μm thick steel wire, and had an internal diameter of 700 μm, with their pitches ranging between 400 and 700 μm. All coils were 8 mm in length, with an approximately 2 mm gap between the foil and beginning of the coil due to the delay line.

The primary diagnostic utilized was the Thomson parabola spectrometer (TPS), which was placed approximately 67 cm from the interaction point, the axis of which was aligned through the longitudinal axis of the HC, as shown in Figure 1. This high-precision alignment was achieved by sending a laser pointer from the rear of the TPS towards the interaction point, and making fine adjustments to the angle of the TPS until the laser passed through a 10 mm long pre-aligned ‘dummy’ coil (i.e., with no target foil attached). The TPS diagnostic was chosen due to its high spectral resolution, as well as its ability to discriminate between ion species of differing charge-to-mass ratios ( $q/m$ )^[ Reference Gwynne, Kar, Doria, Ahmed, Cerchez, Fernandez, Gray, Green, Hanton, Maclellan, McKenna, Najmudin, Neely, Ruiz, Schiavi, Streeter, Swantusch, Willi, Zepf and Borghesi ^{21 ]}. Contained within the TPS to disperse the ions by energy and $q/m$ were an approximately 1 T magnet and a pair of electric plates, whose electric field could be varied up to 20 kV/cm. Entrance pinholes of 200 μm and 500 μm diameter were used, which provided an energy resolution at 40 MeV of 1.6 and 4 MeV, respectively. Fujifilm BAS-TR image plates (IPs) were chosen as the detector in the TPS, which had been absolutely calibrated, using CR-39 nuclear track detectors, at energies relevant to this work^[ Reference Martin, Ahmed, Doria, Alejo, Clarke, Ferguson, Fernaández-Tobias, Freeman, Fuchs, Green, Green, Gwynne, Hanton, Jarrett, Jung, Kakolee, Krygier, Lewis, McIlvenny, McKenna, Morrison, Najmudin, Naughton, Nersisyan, Norreys, Notley, Roth, Ruiz, Scullion, Zepf, Zhai, Borghesi and Kar ^{22 ]}. In conjunction with the TPS, a stack of RCF, 50 mm × 50 mm in size, was also placed directly in front of the TPS pinhole, with a 3 mm hole drilled through the centre, to allow ions to pass through to the TPS. The stack was composed of four layers of the Gafchromic EBT3 brand of RCF, sandwiched between consecutive layers of 1 mm-thick iron. This configuration results in calculated Bragg peak energies for each layer of 22.5, 33.6, 42.4 and 49.9 MeV, respectively. In addition to providing a coarse resolution proton spectrum to complement the TPS data, the RCF stack also served as a useful diagnostic in determining the beam divergence and pointing stability over the metre-scale distance, which until now has not been directly measured for HC targets. Images of a typical HC used in the experiment, as well as a schematic of the experimental setup, are shown in Figure 1.

Figure 1 (a) An example side profile image of a helical coil target. The inset shows the same coil viewed through the coil axis. For consistency, the first and final turns of the coil were kept on the same side for all targets. (b) Schematic of the experimental setup. Helical coils, 8 mm in length, with a delay line attached between the target foil and coil, were positioned at the laser focus. A Thomson parabola spectrometer (TPS) was positioned approximately 67 cm from the interaction point. A stack of radiochromic film (RCF) with very coarse energy resolution and a 3 mm diameter pinhole drilled through the centre was placed in front of the TPS pinhole, to determine beam pointing across the large distance.

3 Experimental results

Figure 2 shows the results of two example shots (labelled as shots 1 and 2) on HC targets in the campaign. Both coils had an internal diameter of 700 μm. The HC used in shot 1 had an average pitch of approximately 550 μm, and shot 2 had a pitch of approximately 400 μm. The scanned RCF layers, converted to dose, are shown in Figures 2(a)–2(d) and Figures 2(e) and 2(f) for each respective shot. It can be seen that, while both shots had proton flux enter the TPS pinhole, shot 2 was a ‘direct hit’, while the highest-flux region of shot 1 was off, with a calculated beam pointing with respect to the TPS pinhole off by approximately 14 mrad. The blue circle, in the first RCF layer, corresponds to the 2° half-angle aperture that is subtended by the HC inner diameter. The red circles in the final layer show the boundaries of the proton dose profile, which shows that the tight focusing inherent to the HC targets is still maintained over metre-scale distances, with maximum half-angle divergences of 1.5° and 1°, respectively, although there are clearly visible spots of significantly higher dose contained within this area that subtend an even narrower angle than this. That the angle subtended by the proton beam at its spectral peak is smaller than that subtended by the coil itself confirms that the effect of the radial field is one that focuses and collimates the proton beam. In this paper, we have opted to refer to this dual effect simply as ‘focusing’ rather than ‘focusing and collimating’ for brevity. The scanned IPs from the TPS for the two shots are shown in Figures 2(i) and 2(j), respectively. The scans have been converted to the photostimulated luminescence (PSL) factor that is characteristic for IPs^[ Reference Paterson, Clarke, Woolsey and Gregori ^{23 ]}. Ion traces of various different species produced in the interaction are indicated in Figure 2(i), and the insets in the images show a zoomed-in portion of the proton trace, highlighting the high-energy narrowband bunch produced by the coils. The IP scan for shot 2 showed a highly saturated proton trace around the region of peak flux in the high-energy spectral bunch. To mitigate this, multiple scans of the IP were taken, until no saturated regions remained. During analysis, after the calibration from PSL to proton number was performed^[ Reference Martin, Ahmed, Doria, Alejo, Clarke, Ferguson, Fernaández-Tobias, Freeman, Fuchs, Green, Green, Gwynne, Hanton, Jarrett, Jung, Kakolee, Krygier, Lewis, McIlvenny, McKenna, Morrison, Najmudin, Naughton, Nersisyan, Norreys, Notley, Roth, Ruiz, Scullion, Zepf, Zhai, Borghesi and Kar ^{22 ]}, the spectrum was rescaled until the unsaturated regions of the first and final scans matched. For this shot, that rescaling factor was 45 after a total of four scans. The initial scan for shot 1 had no saturated regions in the proton trace, owing to the use of the smaller diameter pinhole for the TPS for that shot (200 μm as opposed to 500 μm).

Figure 2 (a)–(d), (e)–(h) Dose-converted scans of the RCF stack in front of the TPS from two helical coil shots (labelled as shots 1 and 2, respectively) with similar laser and target parameters, as described in the text. Bragg peak energies are displayed for each layer. The hole in the centre was drilled to allow protons to reach the TPS. The red circles highlight the regions (half-angle divergences of ~1.5° and ~1°, respectively) from which the dose was taken to obtain the coarse proton spectrum displayed in (k). The blue circles represent the 2° half-angle aperture subtended by the coils. (i), (j) PSL-converted scans of the image plates used in the TPS for the same shots as in (a)–(d) and (e)–(h), respectively. Ion energies increase going down the image, towards the point of zero deflection. The insets show a zoomed-in section of the IP, with green arrows indicating the narrowband proton bunches. (k) Proton energy spectra obtained for these shots from the RCF (data points) and the TPS. The grey line indicates the spectrum from the fourth scan of the IP in (j), rescaled to the flux level detected in the unsaturated regions of the initial first scan (red). The green curve is the spectrum obtained from the data shown in (i), which did not have any saturated region in its first scan. Saturated regions of shot 2’s first scan (red) are shown as dotted lines. A reference TPS spectrum from a flat foil target (with no HC attached) is shown in black. The 3 $\sigma$ noise level is indicated by the dashed grey line.

The deconvolved spectra from both the RCF and TPS data are shown in Figure 2(k). The RCF spectrum reconstruction was performed according to the procedure described by Nürnberg et al. ^[ Reference Nürnberg, Schollmeier, Brambrink, Blažević, Carroll, Flippo, Gautier, Geibel, Harres, Hegelich, Lundh, Markey, McKenna, Neely, Schreiber and Roth ^{12 ]}, wherein the spectrum at each layer energy is determined from the convolution of an assumed spectrum function and the RCF response function. The RCF dose response for EBT3 was independently calibrated by the group at the Birmingham cyclotron. At each layer, the spectrum temperature, ${k}_{\mathrm{B}}T$ , is independently varied so that the calculated dose deposited in the layer matches the measured dose. It was found that a standard exponential function of the form ${N}_0/E\exp \left(-E/{k}_{\mathrm{B}}T\right)$ best matched RCF spectra with their complementary TPS spectra. This also works even for the heavily modulated, non-exponential spectra produced by an HC, because the temperature is individually optimized for each layer, and by allowing for negative temperatures we can account for those parts where the spectrum increases with increasing energy.

Both HC targets display the characteristic high-flux spectral peak around 40–50 MeV, with cutoffs extending up to 60–70 MeV. The cutoff energies represent an increase of 10–20 MeV over standard flat foil shots, a reference spectrum of which is shown in black in Figure 2. The spectral peaks from the HCs show an increase in flux of an order of magnitude compared to the flat foil spectrum over that energy range. In addition, there is a significant region of depleted proton flux at a lower energy, dipping below the noise level of the detector, just before the spectral peak. This depletion region corresponds with those protons that have most efficiently been trapped and post-accelerated by the focusing fields of the EMP, thus causing an absence of protons at that energy after the HC. This feature of HC proton spectra could prove useful in terms of transmission efficiency when one attempts to separate the high-energy HC bunch from the lower-energy proton flux, for example, via the use of a quadrupole setup^[ Reference Pommarel, Vauzour, Meégnin-Chanet, Bayart, Delmas, Goudjil, Nauraye, Letellier, Pouzoulet, Schillaci, Romano, Scuderi, Cirrone, Deutsch, Flacco and Malka ^{24 ]}. It can also be observed that the energy ranges covered by the spectral peak, as well as the region of depleted flux, increase as the pitch of the HC increases, which is consistent with the theory that the energy of protons synchronized with the EMP and the subsequent energy of the post-accelerated bunch increased with increasing pitch.

Figure 3 shows the results for another HC target, with both pitch and internal diameter of 700 μm, the longest pitch of all HC targets shot. As can be seen by the RCF profiles in Figures 3(a)–3(d), this shot constituted another ‘direct hit’ of the proton peak onto the TPS axis. The scanned IP image contains an inset, highlighting the high-energy narrowband proton bunch that the coil produced. The calculated proton spectra are shown in Figure 3(f). The IP was scanned twice, and spectrum rescaled following the same procedure in Figure 2; however, there was still a region of significant saturation within the proton bunch that was not removed. Using the RCF spectral peak, and the unsaturated regions of the bunch in the TPS data, a Gaussian curve has been fitted to determine approximately the bunch shape. From this fit, the bunch width is calculated to be around 8.5 MeV (FWHM). Integrating this fit, the total proton flux calculated to be contained within this bunch is $4\times {10}^{13}$ sr⁻¹. Using the final RCF layer as a reference of the solid angle subtended by the bunch (~0.3–0.5 msr), the total number of protons accelerated into the bunch by the HC (between 45 and 60 MeV) exceeds ${10}^{10}$ (~3 nC total charge). The bunch peak energy of approximately 52 MeV, extending to a cutoff energy above 60 MeV, represents the highest reported spectral peak energies produced by HC targets to date.

Figure 3 (a)–(d) Dose-converted scans of the RCF stack in front of the TPS for another helical coil shot, showing a ‘direct hit’ of the proton bunch into the TPS. Bragg peak energies of each layer are indicated. The red circle denotes a cone of half-angle divergence approximately 0.75°. (e) PSL-converted IP scan of the same shot; the inset shows a zoomed-in section of the IP, with a green arrow highlighting the narrowband proton bunch. (f) Proton spectrum obtained from RCF and the corresponding TPS data. Data was taken from a second IP scan and rescaled following the same procedure as in Figure 2(k). Nevertheless, the dotted region shows significant saturation still present, which could not be removed via further scanning. The RCF data point at approximately 50 MeV serves as an approximate reference of the peak proton flux (and solid angle subtended by the protons) around that point, and a Gaussian fitting (red dashes) has been performed on the unsaturated data, to show a spectral bunch width of 8.5 MeV (FWHM), centred at 52 MeV.

4 Beam pointing

The proton bunches out of the HCs also demonstrate extremely high precision in terms of the beam pointing across the metre-scale distance of the RCF stack. The centre of the proton bunch was calculated as the region of peak dose deposition in the layer corresponding to the spectral peak as determined in the deconvolved spectra. From this, and the known distances of the RCF from the interaction point, the pointing stability can be calculated. The results for each HC shot are displayed in Figure 4. The position of each data point corresponds to the aforementioned centre point with respect to the TPS pinhole on the RCF, and the radii of the points represent the maximum measured divergence of the bunches. The maximum proton energy measured for each shot, on either TPS or RCF, is represented by the colour scale. The average beam pointing stability and beam divergence (half-angle) across all shots are calculated as $9.6\pm 8$ and $6.2\pm 3$ mrad, respectively, where the stated error is the standard deviation of the data. The extremely narrow divergences, corresponding to $0.35{}^{\circ}\pm 0.17{}^{\circ}$ , are similar to those divergences produced by HC targets described in previous works^[ Reference Kar, Ahmed, Prasad, Cerchez, Brauckmann, Aurand, Cantono, Hadjisolomou, Lewis, Macchi, Nersisyan, Robinson, Schroer, Swantusch, Zepf, Willi and Borghesi ^{16 ,} Reference Ahmed, Hadjisolomou, Naughton, Alejo, Brauckmann, Cantono, Ferguson, Cerchez, Doria, Green, Gwynne, Hodge, Kumar, Macchi, Prasad, Willi, Borghesi and Kar ^{17 ]}, where the measurements were made with RCF stacks placed approximately 10 cm from the interaction point. Thus, it is clear that the proton bunches out of HC targets remain tightly focused even when being transported across very large distances, due to their inherently low divergence and the ballistic propagation after the HC.

Figure 4 Beam pointing with respect to the TPS pinhole. Each position is calculated as the centre of the proton dose on the RCF, in the layer corresponding to peak proton flux for each respective shot. The radii of the data points represent the maximum half-angle divergences (in mrad) subtended by the proton beams in the same layer. The colour scale reflects the maximum proton energy measured by either the RCF or TPS data. The angle subtended by the 3 mm diameter hole to allow protons through to the TPS is indicated in blue. The plot area is with the same size as the RCF layers. The shots shown in Figures 2 and 3 are indicated in the plot.

The largest source of error in the beam pointing out of the HCs is likely to result from two factors; namely, shot-to-shot inaccuracies in alignment of the coils onto the intended axis, and also the effects of the final turn at the exit of the HC. Alignment in vacuum is achieved with two orthogonal high-magnification imaging systems, looking at the vertical and horizontal planes, respectively. If one of these systems were slightly misaligned with respect to the other, there would be a larger range of pointing instability shot-to-shot along that axis compared to the other. The final turn, at the point where the support grounding wire is attached to the coil, has the potential to cause a small deflection of the synchronized proton beam, as the final radial field experienced by these protons is no longer along a helical path, and so is not perfectly uniform across $2\pi$ radians. This small nonuniformity in the radial field, experienced for only a very short time, will cause a deflection in the focused beam that is only detectable over large distances. The grounding wire was always attached, as indicated in Figure 1(a), on the right-hand side, relative to the direction of the proton beam, of the HC exit aperture. This implies that the minute proton deflections caused by the last turn, if occurring, would be to the left of the beam axis (X direction). Evidence for this can be seen in Figure 4, where the horizontal pointing of the proton bunches is predominantly to the left of the TP pinhole aperture. This disparity is not evident in the vertical plane, where pointing instabilities appear to not have a preferred direction.

This hypothesis is tested through the use of the particle tracing code PTRACE^[ Reference Schiavi ^{25 ]}. In these simulations, protons were sent through an approximately 8 mm long coil, of constant diameter and pitch of 700 and 600 μm, respectively. The results of these simulations are shown in Figure 5. Multiple HCs were simulated, and as the HC cannot be rotated in PTRACE, the total length was reduced by one quarter turn each iteration. This small change in total coil length did not appreciably affect the final proton spectrum; however, the azimuthal position of the end point of each HC, denoted by $\Phi$ in the figure, is rotated by $\pi /2$ radians with respect to the other.

Figure 5 PTRACE simulations of helical coils showing the effects of the final turn on long-distance beam pointing. (a)–(f) Virtual RCF images from the initial HC, at a plane 8 cm from the source. Every RCF layer is emulated to match the size of real RCF in the experiment – 50 mm × 50 mm squares. Energies of each RCF layer are shown as labelled, with an energy range of ±2 MeV. (g)–(j) Long-distance virtual RCF at the maximally focused energy (32 MeV), 70 cm from the source, for four different final turn positions. In each successive simulation, the azimuthal position of the end of the HC, $\Phi$ , has changed by one quarter turn. Negative numbers imply the coil is shortening slightly compared to the original simulation. The $x$ - and $y$ -axes are converted to angles to aid interpretation of the beam pointing. The blue circles show the size of the hole in the real RCF used in the experiment, to allow access to the TPS. (k) Proton spectra contained inside a half-angle divergence of 0.5°, for each simulated coil. The slight successive shortening of the coils by one quarter turn has little effect on the final spectrum.

The simulated charge pulse profile was chosen to be similar to what has been experimentally measured on the Vulcan laser under similar conditions^[ Reference Ahmed, Hadjisolomou, Naughton, Alejo, Brauckmann, Cantono, Ferguson, Cerchez, Doria, Green, Gwynne, Hodge, Kumar, Macchi, Prasad, Willi, Borghesi and Kar ^{17 ]}; an asymmetric Gaussian with 10 ps half-width at half-maximum (HWHM) rise time, 17 ps HWHM decay time and a peak linear charge density of 45 μC/m. The pulse was initiated with a velocity of 0.98 $c$ . A broadband proton source with a nominal divergence of 5°, and ranging in energy from 10 to 50 MeV, was injected into the HC. In total, 10⁵ protons were simulated for each HC.

Figures 5(a)–5(f) show the beam profiles for the initial HC for a range of energies, as labelled, with a range of ±2 MeV, analogous to a virtual RCF stack. These profiles were taken at the plane 8 cm from the source, a typical distance for an RCF stack used in past experiments with HCs. Each beam profile in the figure was made with the area 50 mm $\times$ 50 mm, identical to the RCF layer sizes used in the main experiment. Successive simulations changing the end point azimuthal positions are shown in Figures 5(g)–5(j). Here, only the energy region where protons were maximally focused (32 MeV) is shown, and the plane at which beam profiles were taken was increased to 70 cm, replicating the distance used in the experiment and making the minute deflections visible. The blue circles represent the size of the hole in the real RCF to allow the protons access to the TPS. A clear difference in beam pointing over long distances is observed, which is dependent on the HC’s final turn, with only a small effect on the beam shape due to the slightly shorter length of the HC. The deviation of the beam off-centre is approximately 10 mrad, again closely matching what was observed in experiment. The proton spectra contained inside a 0.5° half-angle divergence are shown in Figure 5(k). The spectrum of protons can be seen to not appreciably change between simulations, highlighting the near-negligible effect of the small shortening of the total HC length.

Previous works have identified that dispersion of the current as it traverses the helix has the effect of modulating the EMP profile, causing oscillations in the sign of the charge as it propagates^[ Reference Bardon, Moreau, Romagnani, Rousseaux, Ferri, Lefévre, Lantuéjoul, Etchessahar, Bazzoli, Farcage, Maskrot, Serres, Chevrot, Loyez, Veuillot, Cayzac, Vauzour, Boutoux, Sary, La Fontaine, Gremillet, Poyé, Humiéres and Tikhonchuk ^{18 ,} Reference Liu, Mei, Kong, Pan, Xu, Gao, Shou, Wang, Cao, Liang, Peng, Zhao, Chen, Song, Chen, Xu, Yan and Ma ^{19 ,} Reference Hirsch-Passicos, Lacoste, Andreé, Elskens, D’Humieères, Tikhonchuk and Bardon ^{26 ]}. PTRACE does not take into account the effects of said dispersion. However, it can be seen from the simulations presented in the referenced papers (which used HC pitch and radii similar to here) that the current modulations only become significant for the synchronized protons after lengths of approximately 8–10 mm. Indeed, all coils simulated in the referenced papers ranged from 15 to 40 mm in length. As all HCs described in this paper were 8 mm in total length or less, it is reasonable to assume that current dispersion does not have a significant effect on the output proton beams.