1 Motivation
The increasing availability of multi-hundred TW and PW lasers[Reference Danson, Hillier, Hopps and Neely1] brings the confirmation of long-predicted phenomena of strong-field quantum electrodynamics (QED)[Reference Marklund and Shukla2, Reference Di Piazza, Müller, Hatsagortsyan and Keitel3] closer. A multitude of effects on the polarization, wavevector and frequency of photons that probe the polarization of the charged virtual pairs of the vacuum have been theoretically investigated. All of these effects can be understood in terms of the single process of ‘photon–photon scattering’. The current best experimental limit on the predicted cross-section for photon–photon scattering using just high-power laser pulses lies eighteen orders of magnitude above QED[Reference Bernard, Moulin, Amiranoff, Braun, Chambaret, Darpentignz, Grillon, Ranc and Perrone4], but recent laser-cavity experiments such as BMV[Reference Cadène, Berceau, Fouché, Battesti and Rizzo5] and PVLAS[Reference Della Valle, Milotti, Ejlli, Messineo, Piemontese, Zavattini, Gastaldi, Pengo and Ruoso6] have reduced this to six and three orders of magnitude, respectively (or three orders of magnitude and a factor 50, respectively, at the level of the refractive index). Moreover, coinciding with the completion of the XFEL laser at DESY, an experiment at the HIBEF facility[Reference Schlenvoigt, Heinzl, Schramm, Cowan and Sauerbrey7] plans to measure one manifestation of photon–photon scattering, namely the birefringence of the vacuum, using the XFEL beam and a ![]() $1~\text{PW}$ optical laser. This has generated much interest in vacuum polarization effects.
$1~\text{PW}$ optical laser. This has generated much interest in vacuum polarization effects.
The aims of this work are two-fold. First, the main analytical approaches used to study photon–photon scattering will be shown to be essentially equivalent for predictions of planned laser experiments. Second, an overview of the predicted signatures of real photon–photon scattering in various experimental scenarios will be provided, which is also hoped to be useful for the nonspecialist and, in particular, promote discussions between theorists and experimentalists.
2 Introduction: vacuum polarization
Vacuum polarization, depicted in the Feynman diagram of Figure 1, is a basic radiative correction that modifies the propagation of photons in vacuum through the appearance of virtual pairs in a ‘fermion loop’.

Figure 1. Vacuum polarization loop in QED. Wavy and straight lines represent photons and fermions (electrons and positrons), respectively.
There are two complementary interpretations of this effect. The first is based on what is called ‘old-fashioned’ perturbation theory which emphasizes energy considerations at the price of manifest covariance[Reference Weinberg8]. In this interpretation, Heisenberg’s uncertainty relation is invoked to show how quantum mechanics predicts energy and momentum conservation may be violated. The amount of this violation is inversely proportional to the space–time scale over which it occurs. This effect is represented by short-lived ‘virtual’ particles. The second, equivalent interpretation is manifestly covariant and regards the virtual pairs as quantum fluctuations. In this interpretation, at any space–time point there is a nonvanishing probability amplitude for a photon to fluctuate into a pair (or a pair and a photon or in fact any number of particles allowed by the original photon quantum numbers). In this view, energy–momentum conservation is not violated, but the virtual particles do not obey Einstein’s famous equation relating energy and mass.
The main physical effect of vacuum polarization is charge renormalization due to polarization screening as explained in any standard quantum field theory text[Reference Peskin and Schroeder9]. The electric charge of a particle increases as one ‘dives’ into its virtual polarization cloud, hence with decreasing distance from the particle. As a result, the electric charge becomes scale-dependent which may be expressed in terms of a distance-dependent fine structure constant, ![]() ${\it\alpha}={\it\alpha}(R)$. At distances large compared to the electron Compton wavelength,
${\it\alpha}={\it\alpha}(R)$. At distances large compared to the electron Compton wavelength, ![]() $R=ƛ_{e}=\hslash /mc$, the typical length scale of QED, one has
$R=ƛ_{e}=\hslash /mc$, the typical length scale of QED, one has ![]() ${\it\alpha}=e^{2}/4{\it\pi}\hslash c\simeq 1/137$. However, at the much smaller Compton wavelength of, say, the
${\it\alpha}=e^{2}/4{\it\pi}\hslash c\simeq 1/137$. However, at the much smaller Compton wavelength of, say, the ![]() $Z$ boson,
$Z$ boson, ![]() $R=ƛ_{Z}=\hslash /M_{Z}c$, the QED coupling
$R=ƛ_{Z}=\hslash /M_{Z}c$, the QED coupling ![]() ${\it\alpha}$ increases to
${\it\alpha}$ increases to ![]() ${\it\alpha}(ƛ_{Z})\simeq 1/128$.
${\it\alpha}(ƛ_{Z})\simeq 1/128$.
At typical laser energies, the dominant screening particles are indeed pairs of virtual electrons and positrons. Their (virtual) presence may be probed by coupling them to additional photons (see Figure 2), which may represent either fluctuating quantum fields or classical background fields such as provided by lasers. In either case, we are led to consider the probing of vacuum polarization by ‘photon–photon scattering’. When large numbers of photons are involved, a classical metaphor of this quantum effect is of charged vacuum pairs forming a polarizable ‘vacuum plasma’ medium with a nonlinear susceptibility and permeability. An important consequence of this quantum correction to Maxwell’s equations is the violation of the principle of superposition for electromagnetic waves in vacuum.
3 Analytical methods
The microscopic theory describing laser–matter or laser–laser interactions is QED described by the Lagrangian
![]()
the separate terms representing the Dirac, Maxwell and interaction Lagrangians, respectively. The latter derives from ‘minimal substitution’, that is the replacement of the ordinary by the covariant derivative, ![]() $\text{i}\partial \rightarrow \text{i}\partial -eA\equiv \text{i}D_{A}$ in the free Dirac term, which leads to the usual coupling of the photon field
$\text{i}\partial \rightarrow \text{i}\partial -eA\equiv \text{i}D_{A}$ in the free Dirac term, which leads to the usual coupling of the photon field ![]() $A_{{\it\mu}}$ to the Dirac current
$A_{{\it\mu}}$ to the Dirac current ![]() $j^{{\it\mu}}=e\bar{{\it\psi}}{\it\gamma}^{{\it\mu}}{\it\psi}$ as
$j^{{\it\mu}}=e\bar{{\it\psi}}{\it\gamma}^{{\it\mu}}{\it\psi}$ as ![]() An intense laser field will normally be included as a classical, external background field
An intense laser field will normally be included as a classical, external background field ![]() $A_{\text{ext}}$ by the prescription of replacing
$A_{\text{ext}}$ by the prescription of replacing ![]() $A\rightarrow A+A_{\text{ext}}$ in the interaction term only. This guarantees that
$A\rightarrow A+A_{\text{ext}}$ in the interaction term only. This guarantees that ![]() $A_{\text{ext}}$ is not altered by the interaction because the Maxwell term will only contain the field strength tensor built from the fluctuating fields
$A_{\text{ext}}$ is not altered by the interaction because the Maxwell term will only contain the field strength tensor built from the fluctuating fields ![]() $A_{{\it\mu}}$, i.e.,
$A_{{\it\mu}}$, i.e., ![]() $F_{{\it\mu}{\it\nu}}=\partial _{{\it\mu}}A_{{\it\nu}}-\partial _{{\it\nu}}A_{{\it\mu}}$.
$F_{{\it\mu}{\it\nu}}=\partial _{{\it\mu}}A_{{\it\nu}}-\partial _{{\it\nu}}A_{{\it\mu}}$.
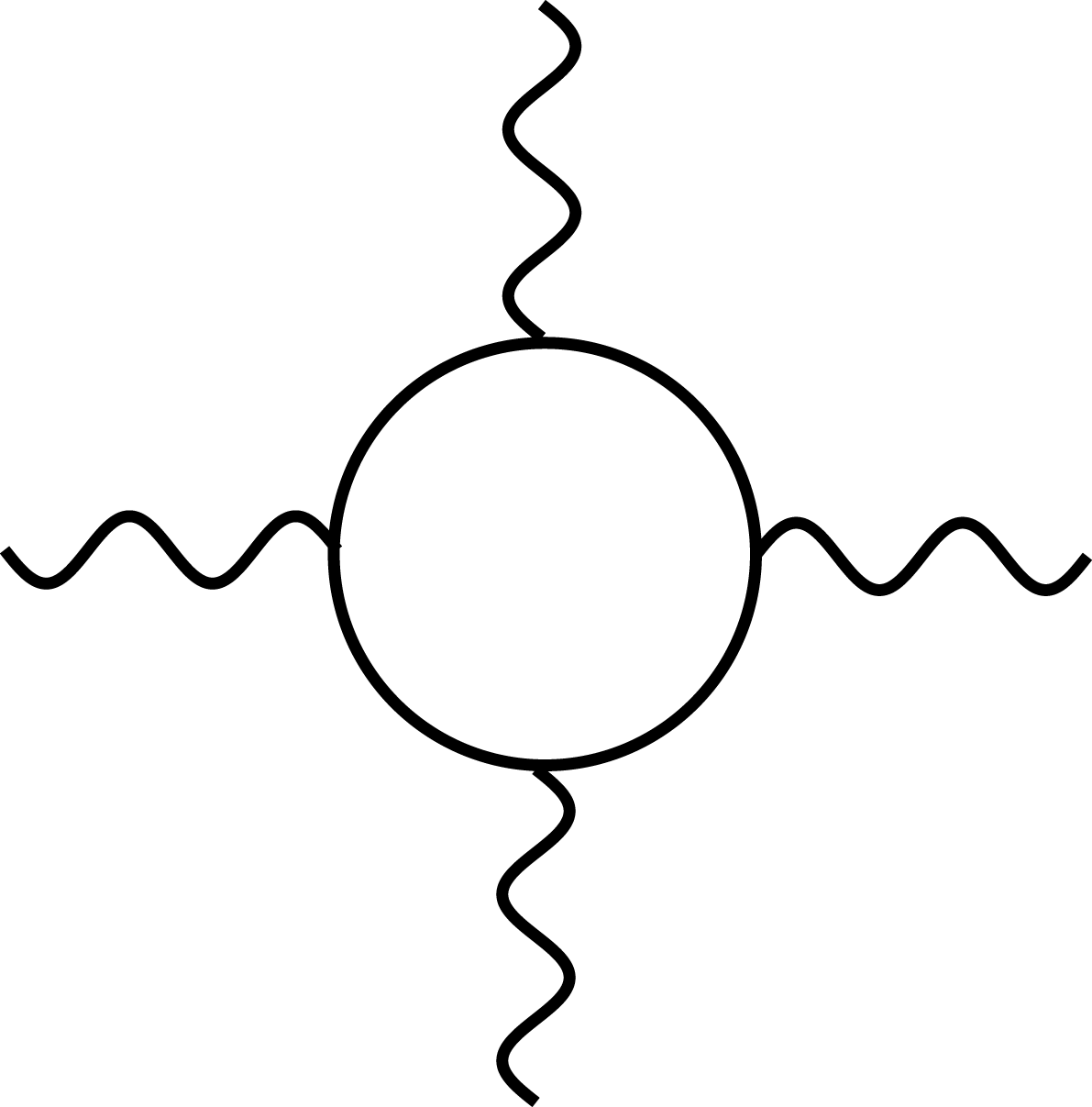
Figure 2. Probing vacuum polarization by photon–photon scattering.
In this contribution we are interested in laser–laser interactions. In this case, the centre-of-mass energy (even for x-rays) will always be much lower than the electron rest energy, ![]() $mc^{2}$. It is thus sufficient to work with the low-energy effective field theory obtained from the QED Lagrangian by ‘integrating out’ the Dirac fields. This can be done by employing the functional integral representation of the QED vacuum persistence amplitude
$mc^{2}$. It is thus sufficient to work with the low-energy effective field theory obtained from the QED Lagrangian by ‘integrating out’ the Dirac fields. This can be done by employing the functional integral representation of the QED vacuum persistence amplitude ![]() $Z$ relating in and out vacua:
$Z$ relating in and out vacua:
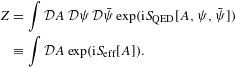 $$\begin{eqnarray}\displaystyle Z & = & \displaystyle \int {\mathcal{D}}A\,{\mathcal{D}}{\it\psi}\,{\mathcal{D}}\bar{{\it\psi}}\exp (\text{i}S_{\text{QED}}[A,{\it\psi},\bar{{\it\psi}}])\nonumber\\ \displaystyle & \equiv & \displaystyle \int {\mathcal{D}}A\exp (\text{i}S_{\text{eff}}[A]).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z & = & \displaystyle \int {\mathcal{D}}A\,{\mathcal{D}}{\it\psi}\,{\mathcal{D}}\bar{{\it\psi}}\exp (\text{i}S_{\text{QED}}[A,{\it\psi},\bar{{\it\psi}}])\nonumber\\ \displaystyle & \equiv & \displaystyle \int {\mathcal{D}}A\exp (\text{i}S_{\text{eff}}[A]).\end{eqnarray}$$In the second step, the fermionic degrees of freedom have been integrated out by performing a Gaussian integral resulting in a fermionic determinant,
![]()
where we have re-exponentiated using ![]() $\text{Det}=\exp \text{Tr}\ln$. The fermionic determinant depends on the photon field
$\text{Det}=\exp \text{Tr}\ln$. The fermionic determinant depends on the photon field ![]() $A$ and can only be evaluated analytically for special configurations such as constant fields. Alternatively, one may perform a derivative (i.e., low-energy) expansion[Reference Gusynin and Shovkovy10, Reference Dunne and Hall11], the leading order of which coincides with the constant field evaluation. For QED this has been done long ago (using different techniques)[Reference Heisenberg and Euler12–Reference Schwinger14], the result being the celebrated Heisenberg–Euler Lagrangian
$A$ and can only be evaluated analytically for special configurations such as constant fields. Alternatively, one may perform a derivative (i.e., low-energy) expansion[Reference Gusynin and Shovkovy10, Reference Dunne and Hall11], the leading order of which coincides with the constant field evaluation. For QED this has been done long ago (using different techniques)[Reference Heisenberg and Euler12–Reference Schwinger14], the result being the celebrated Heisenberg–Euler Lagrangian
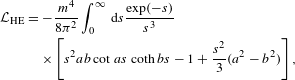 $$\begin{eqnarray}\displaystyle {\mathcal{L}}_{\text{HE}} & = & \displaystyle -\frac{m^{4}}{8{\it\pi}^{2}}\int _{0}^{\infty }\,\text{d}s\frac{\exp (-s)}{s^{3}}\nonumber\\ \displaystyle & & \displaystyle \times \left[s^{2}ab\,\text{cot}~as~\text{coth}\,bs-1+\frac{s^{2}}{3}(a^{2}-b^{2})\right],\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{L}}_{\text{HE}} & = & \displaystyle -\frac{m^{4}}{8{\it\pi}^{2}}\int _{0}^{\infty }\,\text{d}s\frac{\exp (-s)}{s^{3}}\nonumber\\ \displaystyle & & \displaystyle \times \left[s^{2}ab\,\text{cot}~as~\text{coth}\,bs-1+\frac{s^{2}}{3}(a^{2}-b^{2})\right],\qquad\end{eqnarray}$$ where the dimensionless secular invariants ![]() $a$ and
$a$ and ![]() $b$ are given by:
$b$ are given by:
These contain the two electromagnetic invariants
with field and dual field strength tensors, electric and magnetic fields (![]() $F^{{\it\mu}{\it\nu}}$,
$F^{{\it\mu}{\it\nu}}$, ![]() $\tilde{F}^{{\it\mu}{\it\nu}}$,
$\tilde{F}^{{\it\mu}{\it\nu}}$, ![]() $\mathbf{E}$ and
$\mathbf{E}$ and ![]() $\mathbf{B}$, respectively) and the critical field strength:
$\mathbf{B}$, respectively) and the critical field strength:
(Note that we now adopt natural units, ![]() $\hslash =c=1$, for the remainder of this section unless otherwise explicitly stated.) The critical, ‘Sauter’[Reference Sauter15] or ‘Schwinger’[Reference Schwinger14] field strength
$\hslash =c=1$, for the remainder of this section unless otherwise explicitly stated.) The critical, ‘Sauter’[Reference Sauter15] or ‘Schwinger’[Reference Schwinger14] field strength ![]() $E_{\text{cr}}$ is built from the fundamental constants of QED and is the typical field-scale separating weak (
$E_{\text{cr}}$ is built from the fundamental constants of QED and is the typical field-scale separating weak (![]() $E\ll E_{\text{cr}}$) from strong-field (
$E\ll E_{\text{cr}}$) from strong-field (![]() $E>E_{\text{cr}}$) vacuum polarization phenomena.
$E>E_{\text{cr}}$) vacuum polarization phenomena.
The Heisenberg–Euler Lagrangian (Equation (4)) is equivalent to QED for arbitrary values of the field strength but at energies small compared to ![]() $mc^{2}$. For the foreseeable future, laser experiments will stay well below the critical field strength, hence in the weak-field limit. Thus, to a very good approximation, it is sufficient to work with the leading order in a field strength expansion of Equation (4) given by:
$mc^{2}$. For the foreseeable future, laser experiments will stay well below the critical field strength, hence in the weak-field limit. Thus, to a very good approximation, it is sufficient to work with the leading order in a field strength expansion of Equation (4) given by:
with dimensionless low-energy constants
These define effective vertices corresponding to the low-energy limit of the diagram in Figure 2 with the fermion loop no longer being resolved, see Figure 3.
The cross-section for the low-energy limit of real photon–photon scattering depicted in Figure 3 is given by[Reference De Tollis16]:
whereas the high-energy limit is given by[Reference Akhieser, Landau and Pomeranchook17–Reference Berestetskii, Lifshitz and Pitaevskii19]:
The maximum of the cross-section is at the pair-creation threshold of colliding photon centre-of-mass energies ![]() ${\it\omega}=m$.
${\it\omega}=m$.
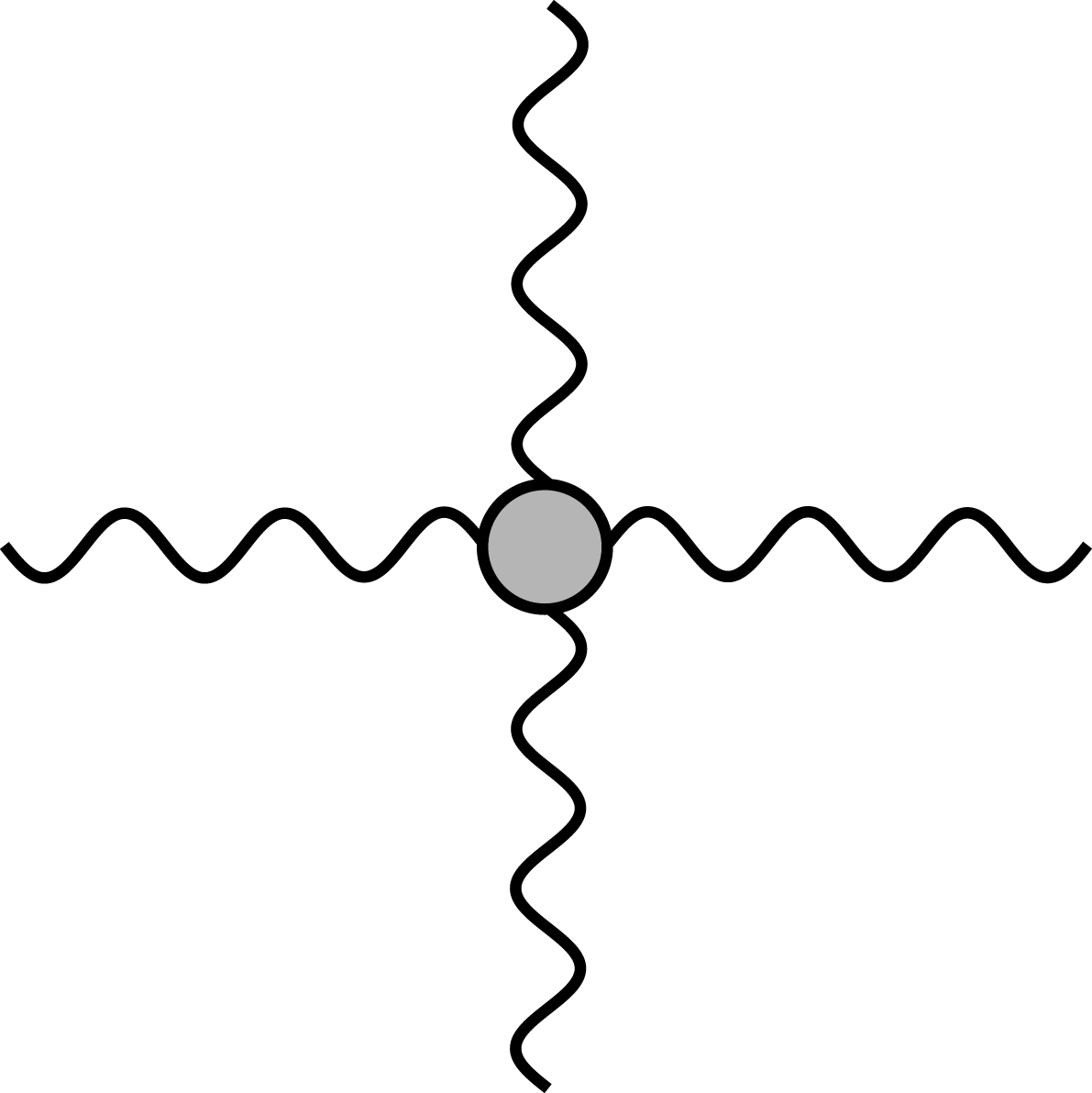
Figure 3. The leading-order Heisenberg–Euler vertex or photon–photon scattering at low energies.
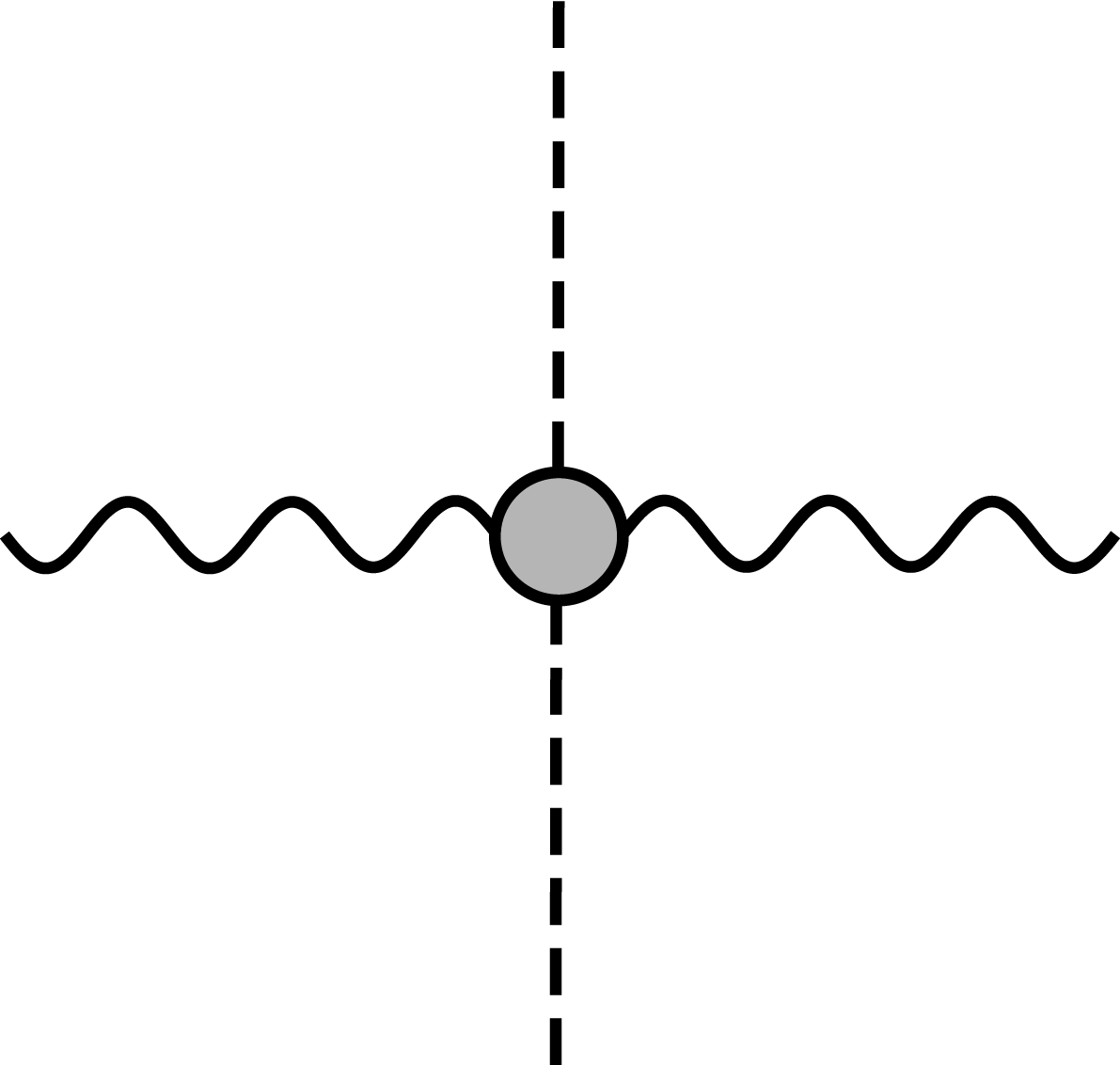
Figure 4. A probe photon (wavy lines) scattering off a classical laser background (dashed lines) at low energy (so that the Heisenberg–Euler vertex can be employed).
3.1 Scattering matrix
In what follows, we will consider a modification of the 4-photon scattering amplitude at low energy by assuming that two of the photons involved are stemming from a high-intensity laser which is probed by a dynamical photon ‘passing through’. This is visualized in Figure 4.
We assume that an incoming probe photon with four-momentum ![]() $k$ and four-polarization
$k$ and four-polarization ![]() ${\it\varepsilon}$ scatters off a laser background described by a field strength tensor
${\it\varepsilon}$ scatters off a laser background described by a field strength tensor ![]() $F_{{\it\mu}{\it\nu}}$ resulting in an outgoing photon with quantum numbers
$F_{{\it\mu}{\it\nu}}$ resulting in an outgoing photon with quantum numbers ![]() $k^{\prime }$ and
$k^{\prime }$ and ![]() ${\it\varepsilon}^{\prime }$. The resulting scattering amplitude is given by the
${\it\varepsilon}^{\prime }$. The resulting scattering amplitude is given by the ![]() $S$-matrix element
$S$-matrix element
Using the leading-order Lagrangian (Equation (8)), using ![]() $S_{\text{fi}}(q)$ to denote
$S_{\text{fi}}(q)$ to denote ![]() $S_{fi}({\it\varepsilon}^{\prime },k^{\prime },{\it\varepsilon},k)$, the
$S_{fi}({\it\varepsilon}^{\prime },k^{\prime },{\it\varepsilon},k)$, the ![]() $S$-matrix element takes on the simple form of a Fourier integral
$S$-matrix element takes on the simple form of a Fourier integral
where ![]() $q=k^{\prime }-k$ is the momentum transfer and
$q=k^{\prime }-k$ is the momentum transfer and
employing the abbreviated scalar products ![]() $(k,F{\it\varepsilon})\equiv k_{{\it\mu}}F^{{\it\mu}{\it\nu}}{\it\varepsilon}_{{\it\nu}}$, etc. Hence, one may introduce an intensity form factor,
$(k,F{\it\varepsilon})\equiv k_{{\it\mu}}F^{{\it\mu}{\it\nu}}{\it\varepsilon}_{{\it\nu}}$, etc. Hence, one may introduce an intensity form factor,
which is the Fourier transformation of the background intensity distribution. In terms of the latter, the scattering amplitude may be written as
The results above are reminiscent of elastic electron nucleus scattering, where the scattering amplitude is proportional to the nuclear charge form factor which is nothing but the Fourier transform of the nuclear charge distribution. In photon–photon scattering, one is naturally probing an intensity, rather than a charge, distribution. To proceed, one has to choose a suitable laser background field, ![]() $F_{{\it\mu}{\it\nu}}(x)$, and calculate its intensity form factor (Equation (13)).
$F_{{\it\mu}{\it\nu}}(x)$, and calculate its intensity form factor (Equation (13)).
3.2 Polarization operator
An equivalent representation is obtained in terms of a quantity aptly called the polarization operator, denoted ![]() ${\rm\Pi}^{{\it\mu}{\it\nu}}$. In its simplest incarnation it is just the mathematical expression for the Feynman diagram of Figure 1, namely
${\rm\Pi}^{{\it\mu}{\it\nu}}$. In its simplest incarnation it is just the mathematical expression for the Feynman diagram of Figure 1, namely
![]()
where the trace ![]() $\text{tr}_{{\it\gamma}}$ extends over the Dirac matrices
$\text{tr}_{{\it\gamma}}$ extends over the Dirac matrices ![]() ${\it\gamma}^{{\it\mu}}$. One may generalize this to the polarization tensor in an external field
${\it\gamma}^{{\it\mu}}$. One may generalize this to the polarization tensor in an external field ![]() $A_{\text{ext}}$, where one trades the free fermion propagators for interacting ones through the standard minimal substitution
$A_{\text{ext}}$, where one trades the free fermion propagators for interacting ones through the standard minimal substitution ![]() $p\rightarrow p-eA_{\text{ext}}$. Indeed, this method has a long history[Reference Toll20–Reference Meuren, Keitel and Di Piazza23] as reviewed by Ref. [Reference Dittrich and Gies24]. For our purposes it is sufficient to just employ the first-order weak-field Heisenberg–Euler Lagrangian (Equation (8)) once again and rewrite it as
$p\rightarrow p-eA_{\text{ext}}$. Indeed, this method has a long history[Reference Toll20–Reference Meuren, Keitel and Di Piazza23] as reviewed by Ref. [Reference Dittrich and Gies24]. For our purposes it is sufficient to just employ the first-order weak-field Heisenberg–Euler Lagrangian (Equation (8)) once again and rewrite it as
with the polarization tensor thus defining the second-order term. From Equation (8) one can straightforwardly read off that
where the background field strength ![]() $F^{{\it\mu}{\it\nu}}=\partial ^{{\it\mu}}A_{\text{ext}}^{{\it\nu}}-\partial ^{{\it\nu}}A_{\text{ext}}^{{\it\mu}}$.
$F^{{\it\mu}{\it\nu}}=\partial ^{{\it\mu}}A_{\text{ext}}^{{\it\nu}}-\partial ^{{\it\nu}}A_{\text{ext}}^{{\it\mu}}$.
To connect this approach with the ![]() $S$ matrix formalism we specialize to forward scattering by setting
$S$ matrix formalism we specialize to forward scattering by setting ![]() $k=k^{\prime }$ in Equation (12) which yields the relation
$k=k^{\prime }$ in Equation (12) which yields the relation
This makes the link between the polarization operator and scattering matrix approaches manifest.
3.3 Modified Maxwell equations
In standard quantum field theory notion[Reference Peskin and Schroeder9], the total Heisenberg–Euler action, ![]() $S_{\text{eff}}=\int d^{4}x\,{\mathcal{L}}_{\text{eff}}$, is nothing but the one-loop effective (or quantum) action of QED evaluated at low energies where there are no external electron lines. The associated effective Lagrangian is the sum of the classical Maxwell term
$S_{\text{eff}}=\int d^{4}x\,{\mathcal{L}}_{\text{eff}}$, is nothing but the one-loop effective (or quantum) action of QED evaluated at low energies where there are no external electron lines. The associated effective Lagrangian is the sum of the classical Maxwell term ![]() ${\mathcal{L}}_{\text{M}}=(E^{2}-B^{2})/2$ and the first quantum correction:
${\mathcal{L}}_{\text{M}}=(E^{2}-B^{2})/2$ and the first quantum correction:
By variation of the quantum action, one can derive the corresponding modified Maxwell equations[Reference Akhiezer and Berestetskii25]:
in which:
and the vacuum polarization and magnetization are:
The wave equations:
can be solved using, for example, the method of Green’s functions.
4 Signatures of vacuum polarization
The most general vacuum polarization diagram represents an elastic scattering amplitude that relates an incoming ensemble of photons ![]() $|k_{1},\ldots ,k_{n}\rangle$, which interact in some experimental scenario, to an outgoing ensemble of photons
$|k_{1},\ldots ,k_{n}\rangle$, which interact in some experimental scenario, to an outgoing ensemble of photons ![]() $|k_{1}^{\prime },\ldots ,k_{n^{\prime }}^{\prime }\rangle$. In this review, we concentrate on processes that could be measured using high-power lasers. The fields of these lasers are included in calculations in various ways. A ‘monochromatic plane wave’ will refer to an infinitely extended wave with no transverse structure, a ‘beam’ will refer to some inclusion of structure, e.g., a cylinder of radiation is a ‘beam’, a ‘focused beam’ will imply some approximation to a real beam with focal width as a parameter and a ‘pulse’ to a field localized in time with pulse duration as a parameter. Since laser pulse wavelengths are much larger than the Compton wavelength, and since expected electric field strengths are much less than the critical Sauter field, equivalent to an intensity of the order of
$|k_{1}^{\prime },\ldots ,k_{n^{\prime }}^{\prime }\rangle$. In this review, we concentrate on processes that could be measured using high-power lasers. The fields of these lasers are included in calculations in various ways. A ‘monochromatic plane wave’ will refer to an infinitely extended wave with no transverse structure, a ‘beam’ will refer to some inclusion of structure, e.g., a cylinder of radiation is a ‘beam’, a ‘focused beam’ will imply some approximation to a real beam with focal width as a parameter and a ‘pulse’ to a field localized in time with pulse duration as a parameter. Since laser pulse wavelengths are much larger than the Compton wavelength, and since expected electric field strengths are much less than the critical Sauter field, equivalent to an intensity of the order of ![]() $10^{29}~\text{W}~\text{cm}^{-2}$, the interaction of laser pulses with virtual electron–positron pairs can be expanded in terms of weak fields. Starting at
$10^{29}~\text{W}~\text{cm}^{-2}$, the interaction of laser pulses with virtual electron–positron pairs can be expanded in terms of weak fields. Starting at ![]() $n=2$ as in Equation (8), each perturbative order describes a vacuum
$n=2$ as in Equation (8), each perturbative order describes a vacuum ![]() $2n$-wave mixing process. It is noteworthy that unlike when real electrons and positrons interact with intense laser fields, for virtual electron–positron pairs, the number of laser photons involved is typically small[Reference Di Piazza26], which is why the discussion is mostly in terms of four-wave mixing processes such as in Figure 5. This means the vacuum is often compared to a nonlinear optical material with a Kerr-like response[Reference Delphenich27]. Although there is a large overlap with nonlinear optics, a major difference is the way the polarization of the dielectric (here, the vacuum) can be shaped by the pump laser pulse.
$2n$-wave mixing process. It is noteworthy that unlike when real electrons and positrons interact with intense laser fields, for virtual electron–positron pairs, the number of laser photons involved is typically small[Reference Di Piazza26], which is why the discussion is mostly in terms of four-wave mixing processes such as in Figure 5. This means the vacuum is often compared to a nonlinear optical material with a Kerr-like response[Reference Delphenich27]. Although there is a large overlap with nonlinear optics, a major difference is the way the polarization of the dielectric (here, the vacuum) can be shaped by the pump laser pulse.
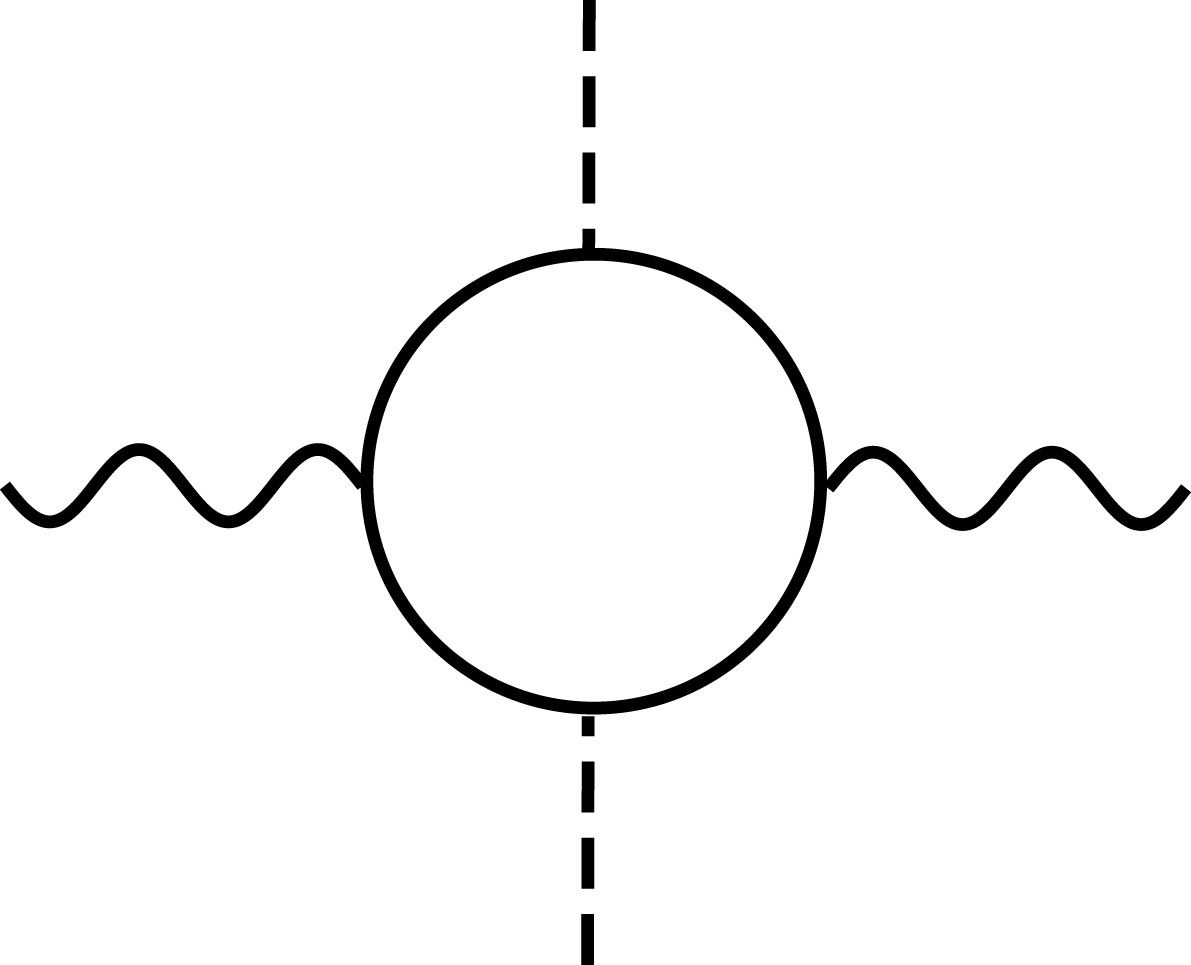
Figure 5. Photons from the pump (dashes) interact with those from the probe to produce a pump-dependent vacuum index of refraction.
The majority of suggested signals of vacuum polarization can be described by considering how the photons from a probe laser change due to interaction with a more intense pump laser. The pump laser will also be referred to as the ‘background’ or the ‘strong field’ where appropriate. The probe laser quantities will often be denoted with subscript ![]() $p$ and the pump or strong laser quantities with the subscript
$p$ and the pump or strong laser quantities with the subscript ![]() $s$. The source of probe photons will mostly be a high-power laser, which, satisfying
$s$. The source of probe photons will mostly be a high-power laser, which, satisfying ![]() $E/E_{\text{cr}}\gg \sqrt{{\it\alpha}}({\it\omega}/m)^{2}$, often allows the external field concept to be invoked for the probe[Reference Narozhny and Fedotov28]. Therefore, the discussion will include interchangeably effects on probe photons and on the probe electromagnetic field, which assumes the photon-scattering process can be summed incoherently over the probe photon distribution. We begin by reviewing the consequence of real photon–photon scattering at the level of probe laser photons:
$E/E_{\text{cr}}\gg \sqrt{{\it\alpha}}({\it\omega}/m)^{2}$, often allows the external field concept to be invoked for the probe[Reference Narozhny and Fedotov28]. Therefore, the discussion will include interchangeably effects on probe photons and on the probe electromagnetic field, which assumes the photon-scattering process can be summed incoherently over the probe photon distribution. We begin by reviewing the consequence of real photon–photon scattering at the level of probe laser photons:
Three measurable quantities have been highlighted – the effect on the probe’s frequency ![]() ${\it\omega}$, its wavevector
${\it\omega}$, its wavevector ![]() $\mathbf{k}$ and its polarization
$\mathbf{k}$ and its polarization ![]() ${\it\varepsilon}(k)$ and these will be discussed in turn.
${\it\varepsilon}(k)$ and these will be discussed in turn.
4.1 Effects on probe photon polarization
Vacuum birefringence refers to the prediction that the refractive index experienced by a probe propagating through regions of intense, but weakly varying strong fields of amplitude ![]() $E_{s}$ is of the form[Reference Toll20, Reference Baier and Breitenlohner29]:
$E_{s}$ is of the form[Reference Toll20, Reference Baier and Breitenlohner29]:
where the ![]() $\Vert$ (
$\Vert$ (![]() $\bot$) indices apply to a probe polarized parallel (perpendicular) to the strong background. This result may be derived from the Heisenberg–Euler quantum equation of motion,
$\bot$) indices apply to a probe polarized parallel (perpendicular) to the strong background. This result may be derived from the Heisenberg–Euler quantum equation of motion,
A plane-wave ansatz for ![]() $A_{{\it\nu}}$ implies two secular equations or dispersion relations,
$A_{{\it\nu}}$ implies two secular equations or dispersion relations,
where ![]() ${\rm\Pi}_{1,2}=c_{1,2}(k,Tk)$ are the two nontrivial eigenvalues of the polarization tensor (Equation (17)), expressed in terms of the background energy–momentum tensor
${\rm\Pi}_{1,2}=c_{1,2}(k,Tk)$ are the two nontrivial eigenvalues of the polarization tensor (Equation (17)), expressed in terms of the background energy–momentum tensor ![]() $T^{{\it\mu}{\it\nu}}=F_{{\it\alpha}}^{{\it\mu}}F^{{\it\alpha}{\it\nu}}$. The dispersion relations (Equation (28)) describe the change in light propagation caused by the energy–momentum density stored in the background field and have been referred to as modified light-cone conditions[Reference Dittrich and Gies30, Reference Shore31]. They imply group velocities different from the vacuum speed of light,
$T^{{\it\mu}{\it\nu}}=F_{{\it\alpha}}^{{\it\mu}}F^{{\it\alpha}{\it\nu}}$. The dispersion relations (Equation (28)) describe the change in light propagation caused by the energy–momentum density stored in the background field and have been referred to as modified light-cone conditions[Reference Dittrich and Gies30, Reference Shore31]. They imply group velocities different from the vacuum speed of light, ![]() $c$, and hence the refractive indices (Equation (26)) different from unity, which can be rewritten as
$c$, and hence the refractive indices (Equation (26)) different from unity, which can be rewritten as ![]() $\mathsf{n}_{\text{vac}}^{\Vert ,\bot }=1+{\rm\Pi}_{1,2}/2{\it\omega}_{p}^{2}$,
$\mathsf{n}_{\text{vac}}^{\Vert ,\bot }=1+{\rm\Pi}_{1,2}/2{\it\omega}_{p}^{2}$, ![]() ${\it\omega}_{p}=k^{0}c$ being the probe frequency.
${\it\omega}_{p}=k^{0}c$ being the probe frequency.
The result for the refractive indices has been shown to hold to all perturbative orders using the polarization operator[Reference Toll20, Reference Shore31, Reference Meuren, Hatsagortsyan, Keitel and Di Piazza32] and Heisenberg–Euler Lagrangian numerically[Reference Ferrando, Michinel, Seco and Tommasini33, Reference Böhl, King and Ruhl34] and analytically[Reference Böhl, King and Ruhl34]. When the pump field is space–time-dependent as is the case for laser pulses, the effect on the probe is calculated by integrating over the inhomogeneous refractive index of the pump background[Reference King, Böhl and Ruhl35]. There has also been recent work indicating finite-time effects in an inhomogeneous background may leave a detectable signal[Reference Hu and Huang36].
Polarization flip is the underlying physical mechanism of vacuum birefringence. The term is used when an incoming photon’s polarization vector ![]() ${\it\varepsilon}^{{\it\mu}}$ is ‘flipped’ to an orthogonal one
${\it\varepsilon}^{{\it\mu}}$ is ‘flipped’ to an orthogonal one ![]() ${\it\varepsilon}^{\prime \,{\it\mu}}$ due to real photon–photon scattering. Linearly polarized probe photons can flip if the background contains some ellipticity and circularly polarized probe photons if the background contains some linear polarization. The flip amplitude (for a head-on collision of probe and background) after a propagation distance
${\it\varepsilon}^{\prime \,{\it\mu}}$ due to real photon–photon scattering. Linearly polarized probe photons can flip if the background contains some ellipticity and circularly polarized probe photons if the background contains some linear polarization. The flip amplitude (for a head-on collision of probe and background) after a propagation distance ![]() $z$ can be found from the Heisenberg–Euler forward scattering amplitude (Equation (18)) and coincides with the birefringence-induced ellipticity[Reference Dinu, Heinzl, Ilderton, Marklund and Torgrimsson37],
$z$ can be found from the Heisenberg–Euler forward scattering amplitude (Equation (18)) and coincides with the birefringence-induced ellipticity[Reference Dinu, Heinzl, Ilderton, Marklund and Torgrimsson37],
where ![]() ${\it\varepsilon}\cdot {\it\varepsilon}^{\prime }=0$. Note the dependence on the difference of the low-energy constants. This implies that a confirmation of vacuum birefringence would rule out other versions of electrodynamics popular in beyond-the-standard-model physics such as Born–Infeld theory, which has
${\it\varepsilon}\cdot {\it\varepsilon}^{\prime }=0$. Note the dependence on the difference of the low-energy constants. This implies that a confirmation of vacuum birefringence would rule out other versions of electrodynamics popular in beyond-the-standard-model physics such as Born–Infeld theory, which has ![]() $c_{1}=c_{2}$[Reference Boillat38–Reference Białynicki-Birula, Jancewicz and Lukierski40]. From Equation (26), the flip amplitude or ellipticity (Equation (29)) has the equivalent representation
$c_{1}=c_{2}$[Reference Boillat38–Reference Białynicki-Birula, Jancewicz and Lukierski40]. From Equation (26), the flip amplitude or ellipticity (Equation (29)) has the equivalent representation
which is proportional to the difference in refractive indices, hence the phase shift between different polarizations.
Detailed calculations have been performed for photons propagating in an arbitrary plane-wave background[Reference Baĭer, Mil’shteĭn and Strakhovenko22, Reference Dinu, Heinzl, Ilderton, Marklund and Torgrimsson37], and the kinematic low-energy limit relevant for laser-based experiments was found to be consistent with use of the Heisenberg–Euler approach for calculating birefringence and ellipticity[Reference Torgrimsson41]. A study of the dependency of the flip and nonflip amplitude on spatial and timing jitter and angle of incidence[Reference Dinu, Heinzl, Ilderton, Marklund and Torgrimsson42] was performed, with the results also being consistent with a previous similar study in the low-energy limit[Reference King and Keitel43]. Both studies[Reference Dinu, Heinzl, Ilderton, Marklund and Torgrimsson42, Reference King and Keitel43] found that modelling the background as a focused paraxial Gaussian beam without taking into account the finite pulse duration led to an order of magnitude discrepancy in the number of scattered photons.
Induced ellipticity is a consequence of birefringence as pointed out in the previous subsection, see Equations (29) and (30). The polarization of a linearly polarized probe plane wave can be described with the vector:
where ![]() ${\it\varphi}$ is the probe phase. If, over some probe phase
${\it\varphi}$ is the probe phase. If, over some probe phase ![]() ${\it\omega}_{p}z$ the
${\it\omega}_{p}z$ the ![]() $\Vert$ and
$\Vert$ and ![]() $\bot$ components experience a different refractive index, then when the phase shift
$\bot$ components experience a different refractive index, then when the phase shift ![]() ${\it\delta}{\it\varphi}^{\Vert ,\bot }=n^{\Vert ,\bot }{\it\omega}_{p}z\ll 1$, the polarization changes to:
${\it\delta}{\it\varphi}^{\Vert ,\bot }=n^{\Vert ,\bot }{\it\omega}_{p}z\ll 1$, the polarization changes to:
and the originally linearly polarized probe is now elliptically polarized. If the background is constant, the ellipticity can be written[Reference Di Piazza, Hatsagortsyan and Keitel44]:
which generalizes Equation (30). The induced ellipticity in the interaction of an x-ray probe plane wave of wavelength ![]() ${\it\lambda}_{p}=0.4~\text{nm}$ counterpropagating with a Gaussian pump beam of intensity
${\it\lambda}_{p}=0.4~\text{nm}$ counterpropagating with a Gaussian pump beam of intensity ![]() $10^{23}~\text{W}~\text{cm}^{-2}$ and wavelength
$10^{23}~\text{W}~\text{cm}^{-2}$ and wavelength ![]() ${\it\lambda}_{s}=745~\text{nm}$ focused to
${\it\lambda}_{s}=745~\text{nm}$ focused to ![]() $8\,{\rm\mu}\text{m}$ was calculated[Reference Di Piazza, Hatsagortsyan and Keitel44] to experience an ellipticity of
$8\,{\rm\mu}\text{m}$ was calculated[Reference Di Piazza, Hatsagortsyan and Keitel44] to experience an ellipticity of ![]() $\mathsf{e}\approx 5\times 10^{-9}~\text{rad}$ when measured at a distance of
$\mathsf{e}\approx 5\times 10^{-9}~\text{rad}$ when measured at a distance of ![]() $0.25~\text{m}$ from the pump–probe collision. By considering the same pump energy distributed over two pump Gaussian laser beams counterpropagating with a Gaussian probe beam, a modest improvement of around
$0.25~\text{m}$ from the pump–probe collision. By considering the same pump energy distributed over two pump Gaussian laser beams counterpropagating with a Gaussian probe beam, a modest improvement of around ![]() $\sqrt{2}$ was found, and the near-field-induced ellipticity[Reference King, Di Piazza and Keitel45]
$\sqrt{2}$ was found, and the near-field-induced ellipticity[Reference King, Di Piazza and Keitel45]
with the effective interaction length between the two Gaussians ![]() $z_{\text{eff.}}$ depending on the probe
$z_{\text{eff.}}$ depending on the probe ![]() $z_{r,p}$ and pump
$z_{r,p}$ and pump ![]() $z_{r,s}$ Rayleigh lengths. This agrees with the expressions calculated for a monochromatic probe plane wave counterpropagating with a Gaussian pump[Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf46] in the limit
$z_{r,s}$ Rayleigh lengths. This agrees with the expressions calculated for a monochromatic probe plane wave counterpropagating with a Gaussian pump[Reference Heinzl, Liesfeld, Amthor, Schwoerer, Sauerbrey and Wipf46] in the limit ![]() $z_{r,p}\rightarrow \infty$.
$z_{r,p}\rightarrow \infty$.
Polarization rotation is the macroscopic consequence of coherent polarization flipping at the photon level. The effect on the transverse photon polarization states in Equations (31) and (32) has the consequence that the polarization angle ![]() ${\it\theta}$ will rotate as the initially linearly polarized probe acquires an ellipticity. The ellipse traced out by the probe field vector can be seen to be[Reference King47]:
${\it\theta}$ will rotate as the initially linearly polarized probe acquires an ellipticity. The ellipse traced out by the probe field vector can be seen to be[Reference King47]:
where ![]() $x\cos {\it\theta}={\it\varepsilon}^{\Vert }$ and
$x\cos {\it\theta}={\it\varepsilon}^{\Vert }$ and ![]() $y\sin {\it\theta}={\it\varepsilon}^{\bot }$. For an x-ray probe counterpropagating with an optical Gaussian pump beam, the rotation angle was found to be the same order of magnitude as the induced ellipticity[Reference Di Piazza, Hatsagortsyan and Keitel44, Reference King, Di Piazza and Keitel45].
$y\sin {\it\theta}={\it\varepsilon}^{\bot }$. For an x-ray probe counterpropagating with an optical Gaussian pump beam, the rotation angle was found to be the same order of magnitude as the induced ellipticity[Reference Di Piazza, Hatsagortsyan and Keitel44, Reference King, Di Piazza and Keitel45].
4.2 Effects on probe photon wavevector
On the photon level, four-wave mixing as depicted in Figure 5 can be understood as two incoming photons, one from the probe and one from the pump, being scattered to two outgoing photons, one being back into the pump field and the other being the signal of the vacuum interaction. Conservation of momentum permits the scattered photons having a wider transverse distribution than the probe and strong background, hence allowing one to spatially separate the photon–photon scattering signal from the large background of pump and probe laser photons.
On the classical level, a refractive index ![]() $\mathsf{n}_{\text{vac}}$ different from unity, implies altered transmitted wavevectors via Snell’s law, and altered transmission
$\mathsf{n}_{\text{vac}}$ different from unity, implies altered transmitted wavevectors via Snell’s law, and altered transmission ![]() $T$ and reflection coefficient
$T$ and reflection coefficient ![]() $R$ via Fresnel’s law at perpendicular incidence[Reference Jackson48]:
$R$ via Fresnel’s law at perpendicular incidence[Reference Jackson48]:
If the vacuum refractive index is written as ![]() $\mathsf{n}_{\text{vac}}=1+{\it\delta}\mathsf{n}_{\text{vac}}$, the effect on probe transmission
$\mathsf{n}_{\text{vac}}=1+{\it\delta}\mathsf{n}_{\text{vac}}$, the effect on probe transmission ![]() ${\sim}O({\it\delta}\mathsf{n}_{\text{vac}})$ whereas the effect on reflection
${\sim}O({\it\delta}\mathsf{n}_{\text{vac}})$ whereas the effect on reflection ![]() ${\sim}O({\it\delta}\mathsf{n}_{\text{vac}}^{2})$.
${\sim}O({\it\delta}\mathsf{n}_{\text{vac}}^{2})$.
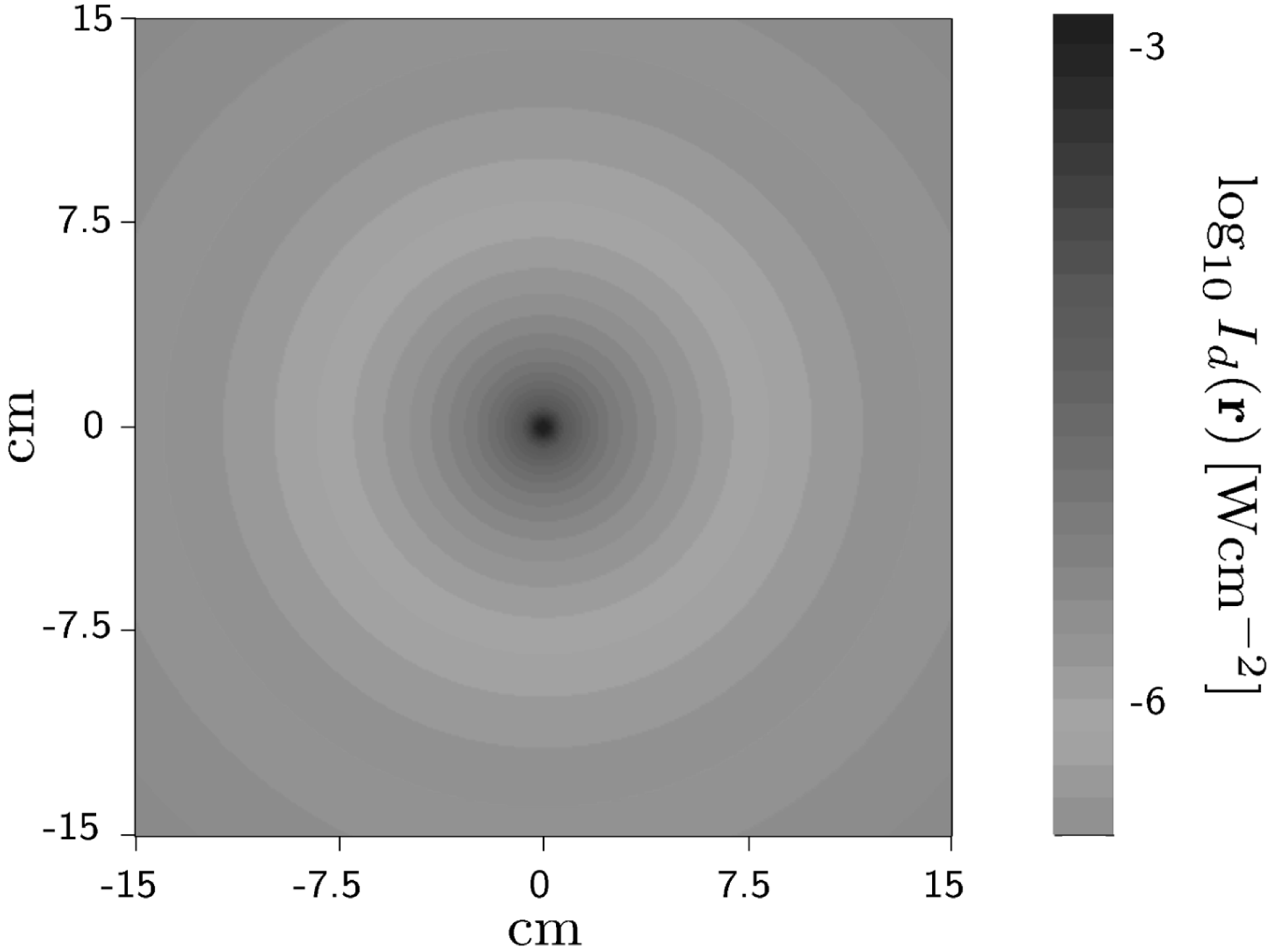
Figure 6. Predicted diffracted electric field in a collision of two counterpropagating Gaussian beams. Adapted from [Reference King47].
If the probe beam is considered to be much wider than the pump background, the region of polarized vacuum can be considered to ‘diffract’ the probe. An example of such a ‘single-slit’ diffraction pattern is given in Figure 6. It is well known that the far-field diffracted field is related to the Fourier transform of the aperture function[Reference Levi49], and via Babinet’s principle, this can be related to an integral over the region of refractive index different from unity. We underline the connection of this classical analogue to the intensity form factor of the scattering matrix approach Equation (13).
Vacuum diffraction was considered in the collision of a plane probe and a focused Gaussian pump beam[Reference Di Piazza, Hatsagortsyan and Keitel44], and extended to the collision of focused Gaussian probe and pump beams[Reference King, Piazza and Keitel50]. The advantage of this signal is that for increasing scattering angle, while the focused laser background is exponentially suppressed, the scattered photon vacuum signal is power-law suppressed. In the detector plane then, the number of scattered photons can be calculated in ‘measurable’ regions, where the signal-to-noise ratio is much larger than unity. One interesting scenario was calculated of colliding two parallel, highly focused Gaussian pump beams with a wide weakly focused Gaussian probe beam, such that the photons scattered in the two slit-like polarized regions around the pump beams would interfere and hence together form an all-optical double-slit experiment[Reference King, Piazza and Keitel50]. For the case of two colliding Gaussian pulses, the dependency of the diffracted photon signal on experimental parameters such as the total beam power, spatial and timing jitter, angle of collision, pulse duration, probe wavelength and focal width has been carried out[Reference King and Keitel43]. With 10 PW total laser power split into pump and probe focused optical pulses, of the order of a few photons were predicted to be diffracted into measurable regions on a detector place 1 m from the interaction centre. These results were verified in a study by different authors[Reference Tommasini and Michinel51], who used a different beam model. The diffraction paradigm was extended from single and double slits to a ‘diffraction grating’ of having a probe beam diffract off a regular series of pump beams[Reference Kryuchkyan and Hatsagortsyan52]. Only on positions of the detector where the Bragg condition:
for integer ![]() $n$, probe wavenumber
$n$, probe wavenumber ![]() $k_{p}$, wavenumber of the pump beam structure
$k_{p}$, wavenumber of the pump beam structure ![]() $q$ and angle between incoming and diffracted probe
$q$ and angle between incoming and diffracted probe ![]() ${\it\theta}$, is there constructive interference of the signal of scattered photons. Since the addition of diffracted waves occurs at the level of the field, and since the number of photons scattered depends upon the total diffracted field squared, there is an enhancement in such a setup proportional to the square of the number of modulation periods. Alternatively, rather than using many beams, a single, wide-angle beam diffracting with itself at the focus has also been studied[Reference Monden and Kodama53], with the conclusion that the number of diffracted photons increases exponentially with the angular aperture. Since only the near-field signal was presented, more work is required to determine measurability in this scheme.
${\it\theta}$, is there constructive interference of the signal of scattered photons. Since the addition of diffracted waves occurs at the level of the field, and since the number of photons scattered depends upon the total diffracted field squared, there is an enhancement in such a setup proportional to the square of the number of modulation periods. Alternatively, rather than using many beams, a single, wide-angle beam diffracting with itself at the focus has also been studied[Reference Monden and Kodama53], with the conclusion that the number of diffracted photons increases exponentially with the angular aperture. Since only the near-field signal was presented, more work is required to determine measurability in this scheme.
The idea of using the diffracted photons’ flipped polarization as well as their altered wavevector in an experimental measurement was explored for the wide-angled single-beam setup[Reference Monden and Kodama53], a single propagating Gaussian beam taking into account higher orders in a Hermite–Gauss expansion[Reference Paredes, Novoa and Tommasini54] and has been most recently applied to the upcoming HIBEF experiment[Reference Karbstein, Gies, Reuter and Zepf55].
Vacuum reflection refers to the back-scattering of photons in real photon–photon scattering. Static magnetic inhomogeneities of the form of a Lorentzian, Gaussian and oscillating Gaussian have been studied[Reference Gies, Karbstein and Seegert56] and more recently static electromagnetic inhomogeneities but most significantly scattering in a Gaussian beam[Reference Gies, Karbstein and Seegert57], although calculations for pulses of a finite duration are still to be performed.
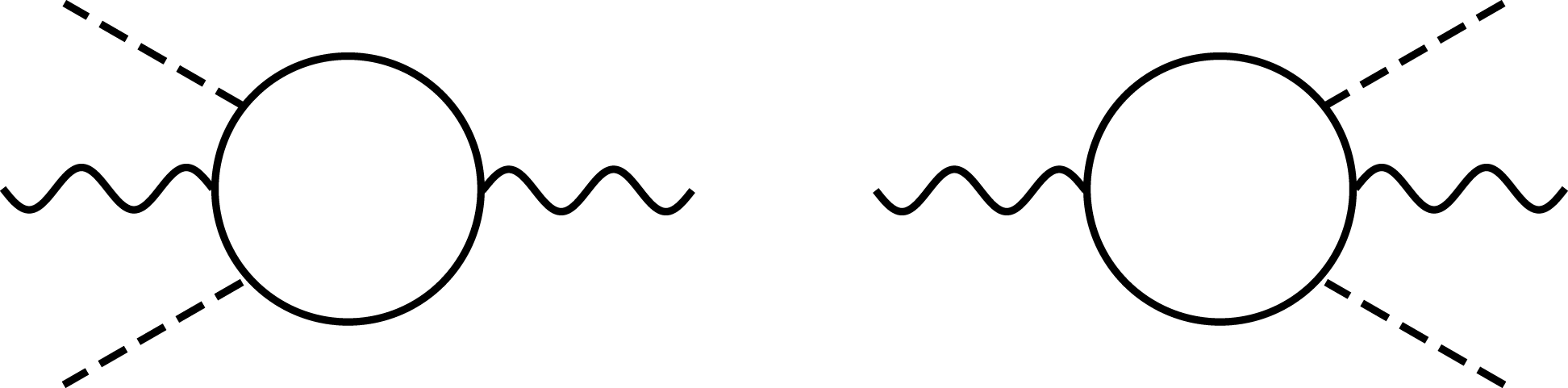
Figure 7. Parametric frequency upshifting (left) and downshifting (right) can occur between pump and probe through the vacuum interaction.
4.3 Effects on probe photon frequency
The frequency of probe photons can change via interaction with the polarized vacuum. However, this effect is much more difficult to measure experimentally because of the limited range of energy and momenta for which it is permitted. Suppose via the four-photon interaction, two photons from the strong pump background merge with a probe photon as depicted in Figure 7. Then via energy–momentum conservation:
but at the same time, the photon must be real to propagate to the detector so ![]() ${\it\omega}^{\prime 2}=\mathbf{k}^{\prime }\boldsymbol{\cdot }\mathbf{k}^{\prime }$. This constrains the allowed frequencies, momenta and angles that can be combined. Similar relations occur for Raman and Brillouin scattering[Reference Moloney and Newell58], except all the waves here are electromagnetic.
${\it\omega}^{\prime 2}=\mathbf{k}^{\prime }\boldsymbol{\cdot }\mathbf{k}^{\prime }$. This constrains the allowed frequencies, momenta and angles that can be combined. Similar relations occur for Raman and Brillouin scattering[Reference Moloney and Newell58], except all the waves here are electromagnetic.
Vacuum parametric frequency shifting has been calculated for special beam configurations. Combining three monochromatic plane waves at right angles, whose wavelengths are 800, 800 and 400 nm, was predicted to produce a signal that is spatially and frequentially (at 267 nm) separated from the background[Reference Lundström, Brodin, Lundin, Marklund, Bingham, Collier, Mendonça and Norreys59]. For respective beam powers 0.1, 0.1 and 0.5 PW, taking the interaction region to be cuboidal, on average 0.07 photons would be frequency-upshifted per collision of the beams, which is predicted to be larger than the Compton-scattering background. A signature of the frequency-shifting four-wave mixing process on the number of total measurable diffracted photons for a collision of two ultra-short focused Gaussian pulses was also calculated[Reference King and Keitel43]. For 10 PW total beam power split into a probe with wavelength 228 nm and duration 2 fs, as the duration of the 910 nm pump is reduced to 1 fs, the total number of diffracted photons is predicted to change by around 20%, equal to one photon per shot. Calculations beyond the paraxial approximation recently performed[Reference Fillion-Gourdeau, Lefebvre and MacLean60] for two co-propagating beams of different frequencies incident on a parabolic mirror suggest 1–10 PW laser beams are required to observe vacuum frequency mixing, although the method of detecting the signal needs to be given more attention.
Vacuum high-harmonic generation can take place if the colliding laser pulses have the same frequency. Then via the four-wave mixing process in Equation (37), if ![]() ${\it\omega}_{p}={\it\omega}_{s,1}={\it\omega}_{s,2}={\it\omega}$, the signal of the vacuum process has a frequency
${\it\omega}_{p}={\it\omega}_{s,1}={\it\omega}_{s,2}={\it\omega}$, the signal of the vacuum process has a frequency ![]() ${\it\omega}^{\prime }=3{\it\omega}$ and so is at the third harmonic of the probe. By considering six-, eight- and in general
${\it\omega}^{\prime }=3{\it\omega}$ and so is at the third harmonic of the probe. By considering six-, eight- and in general ![]() $2n$-wave mixing as depicted in Figure 8, it can be seen that a harmonic spectrum for the vacuum interaction can be produced. As each extra interaction between the virtual pair and a laser photon is weighted at the amplitude level with a factor
$2n$-wave mixing as depicted in Figure 8, it can be seen that a harmonic spectrum for the vacuum interaction can be produced. As each extra interaction between the virtual pair and a laser photon is weighted at the amplitude level with a factor ![]() $E/E_{\text{cr}}\ll 1$, higher harmonics are in general exponentially suppressed. Nevertheless, the harmonic spectrum produced by a standing wave formed of two monochromatic pump laser beams was calculated for subcritical (
$E/E_{\text{cr}}\ll 1$, higher harmonics are in general exponentially suppressed. Nevertheless, the harmonic spectrum produced by a standing wave formed of two monochromatic pump laser beams was calculated for subcritical (![]() $E<E_{\text{cr}}$) strengths where higher harmonic orders
$E<E_{\text{cr}}$) strengths where higher harmonic orders ![]() $j$ were found[Reference Di Piazza, Hatsagortsyan and Keitel61] to follow the hierarchy
$j$ were found[Reference Di Piazza, Hatsagortsyan and Keitel61] to follow the hierarchy ![]() $(E/E_{\text{cr}})^{4j}$. In a setup involving three beams, the minimum power of each laser required to scatter one photon was found to be:
$(E/E_{\text{cr}})^{4j}$. In a setup involving three beams, the minimum power of each laser required to scatter one photon was found to be:
for typical beam cross-sectional dimension ![]() $w_{0}$, interaction duration
$w_{0}$, interaction duration ![]() ${\it\tau}$ and coherence time
${\it\tau}$ and coherence time ![]() ${\it\tau}_{c}$. The most likely frequency of the scattered photon is, however, the fundamental harmonic. The intensity at which a single focused laser pulse will begin to produce harmonics via self-interaction has been studied[Reference Fedotov and Narozhny62], with the conclusion that a pulse of 1000 nm photons focused within a cone of angle 0.1 rad will produce one photon per period at
${\it\tau}_{c}$. The most likely frequency of the scattered photon is, however, the fundamental harmonic. The intensity at which a single focused laser pulse will begin to produce harmonics via self-interaction has been studied[Reference Fedotov and Narozhny62], with the conclusion that a pulse of 1000 nm photons focused within a cone of angle 0.1 rad will produce one photon per period at ![]() $5\times 10^{27}~\text{W}~\text{cm}^{-2}$. A recent calculation of an alternative route to high-harmonic generation through having many scattering events involving low numbers of photons[Reference Lutzky and Toll63–Reference Heyl and Hernquist68] (as in Figure 9) has recently been suggested to be more efficient. For the collision of a Gaussian probe at much higher frequency than the background, if the parameter
$5\times 10^{27}~\text{W}~\text{cm}^{-2}$. A recent calculation of an alternative route to high-harmonic generation through having many scattering events involving low numbers of photons[Reference Lutzky and Toll63–Reference Heyl and Hernquist68] (as in Figure 9) has recently been suggested to be more efficient. For the collision of a Gaussian probe at much higher frequency than the background, if the parameter ![]() $(64{\it\alpha}/105{\it\pi})(E_{s}^{3}E_{p}/E_{\text{cr}}^{4}){\it\omega}_{p}{\it\tau}_{s}$, where
$(64{\it\alpha}/105{\it\pi})(E_{s}^{3}E_{p}/E_{\text{cr}}^{4}){\it\omega}_{p}{\it\tau}_{s}$, where ![]() ${\it\tau}_{s}$ is the duration of the pump, can be made close to unity, harmonic generation will dominate, with the spectrum displaying a power-law behaviour and the appearance of a corresponding electromagnetic shock[Reference Böhl, King and Ruhl34].
${\it\tau}_{s}$ is the duration of the pump, can be made close to unity, harmonic generation will dominate, with the spectrum displaying a power-law behaviour and the appearance of a corresponding electromagnetic shock[Reference Böhl, King and Ruhl34].
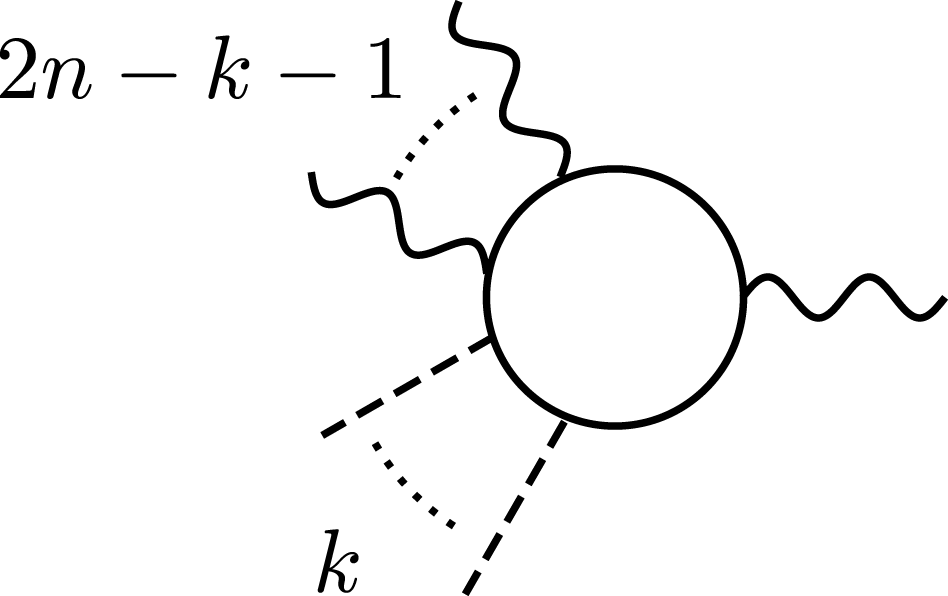
Figure 8. Vacuum high-harmonic generation of the ![]() $n$th harmonic of the probe via
$n$th harmonic of the probe via ![]() $2n$-photon scattering.
$2n$-photon scattering.
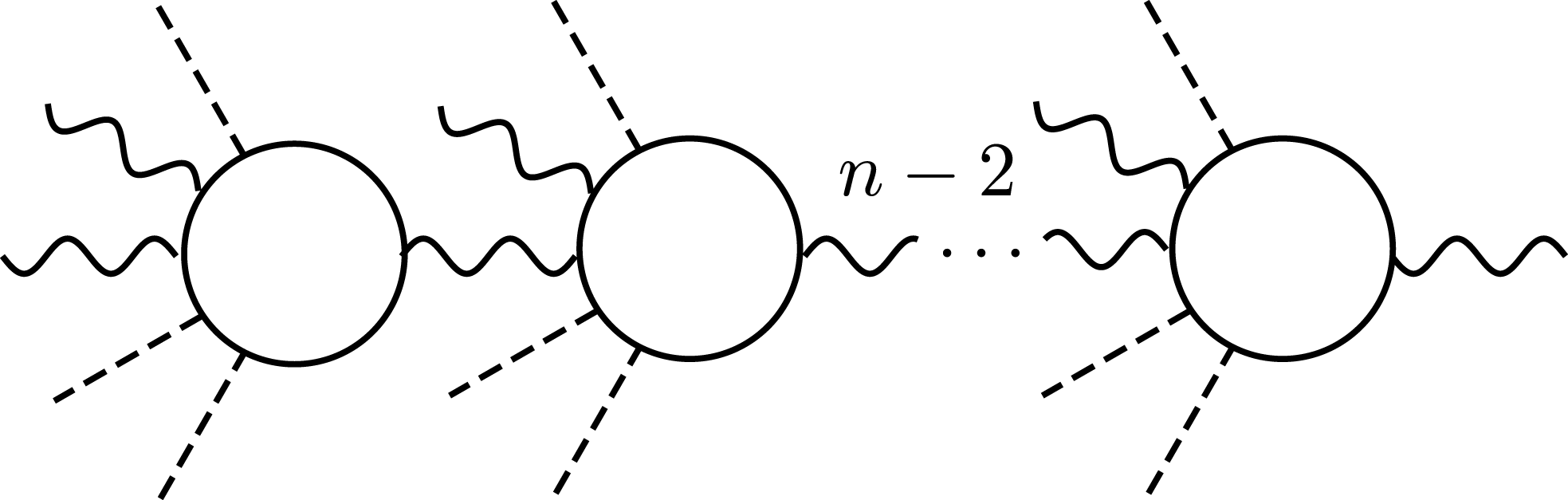
Figure 9. Vacuum high-harmonic generation of the ![]() $n$th harmonic of the probe via a chain of six-photon scattering.
$n$th harmonic of the probe via a chain of six-photon scattering.
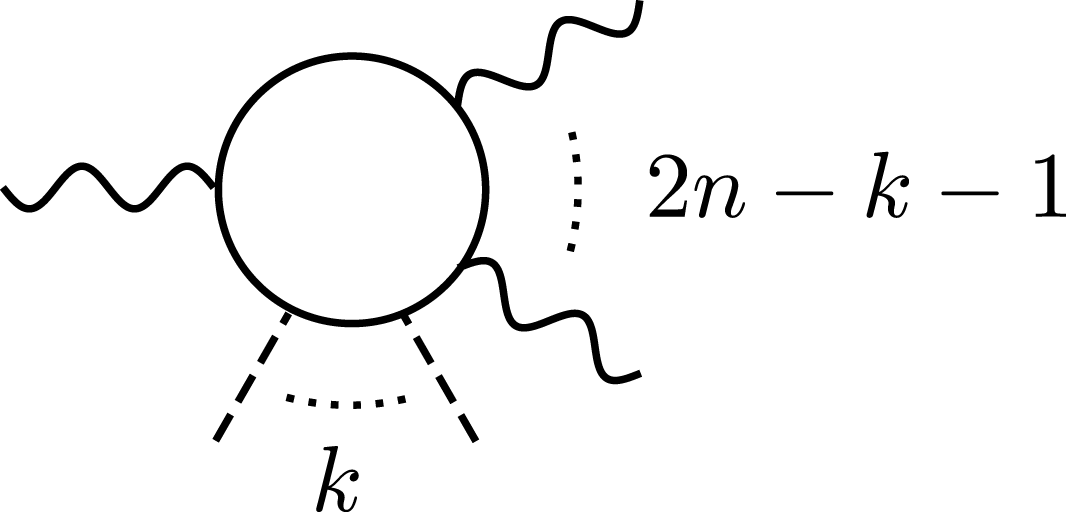
Figure 10. An incoming probe photon can split into ![]() $k$ outgoing ones, due to interaction with the background.
$k$ outgoing ones, due to interaction with the background.
Photon splitting as depicted in Figure 10, is sometimes thought of as the opposite of high-harmonic generation, but unlike harmonic generation, the emitted photons can have a continuum of energies. If one considers splitting to two photons via four-wave mixing then via energy and momentum conservation, one possibility is:
where now two constraints on these equations are ![]() $({\it\omega}_{1,2}^{\prime })^{2}=\mathbf{k}_{1,2}^{\prime }\boldsymbol{\cdot }\mathbf{k}_{1,2}^{\prime }$. The continuum of allowed energies and the possibility for a wide angular distribution of emitted photons makes this process worthy of study. The process has been comprehensively studied for a probe photon propagating through a plane-wave background of arbitrary form and polarization[Reference Di Piazza, Milstein and Keitel69], which was found to depend on the two parameters
$({\it\omega}_{1,2}^{\prime })^{2}=\mathbf{k}_{1,2}^{\prime }\boldsymbol{\cdot }\mathbf{k}_{1,2}^{\prime }$. The continuum of allowed energies and the possibility for a wide angular distribution of emitted photons makes this process worthy of study. The process has been comprehensively studied for a probe photon propagating through a plane-wave background of arbitrary form and polarization[Reference Di Piazza, Milstein and Keitel69], which was found to depend on the two parameters ![]() ${\it\eta}={\it\omega}_{p}{\it\omega}_{s}/m^{2}$ and
${\it\eta}={\it\omega}_{p}{\it\omega}_{s}/m^{2}$ and ![]() ${\it\chi}=({\it\omega}_{p}/m)(E/E_{\text{cr}})$. Two events per hour were predicted using
${\it\chi}=({\it\omega}_{p}/m)(E/E_{\text{cr}})$. Two events per hour were predicted using ![]() $10^{8}$ 250 MeV tagged photons per second almost counterpropagating with 100 fs
$10^{8}$ 250 MeV tagged photons per second almost counterpropagating with 100 fs ![]() $10^{15}~\text{W}~\text{cm}^{-2}$ 1 keV XFEL beams separated by 93 ns. Alternatively, two events per hour were also predicted using
$10^{15}~\text{W}~\text{cm}^{-2}$ 1 keV XFEL beams separated by 93 ns. Alternatively, two events per hour were also predicted using ![]() $10^{8}$ 100 MeV tagged photons counterpropagating with a 1 Hz 1 eV optical pump of intensity
$10^{8}$ 100 MeV tagged photons counterpropagating with a 1 Hz 1 eV optical pump of intensity ![]() $10^{25}~\text{W}~\text{cm}^{-2}$. The conclusion was that a different experimental setup must be considered if this effect is to be observed in the near future[Reference Di Piazza, Milstein and Keitel69].
$10^{25}~\text{W}~\text{cm}^{-2}$. The conclusion was that a different experimental setup must be considered if this effect is to be observed in the near future[Reference Di Piazza, Milstein and Keitel69].
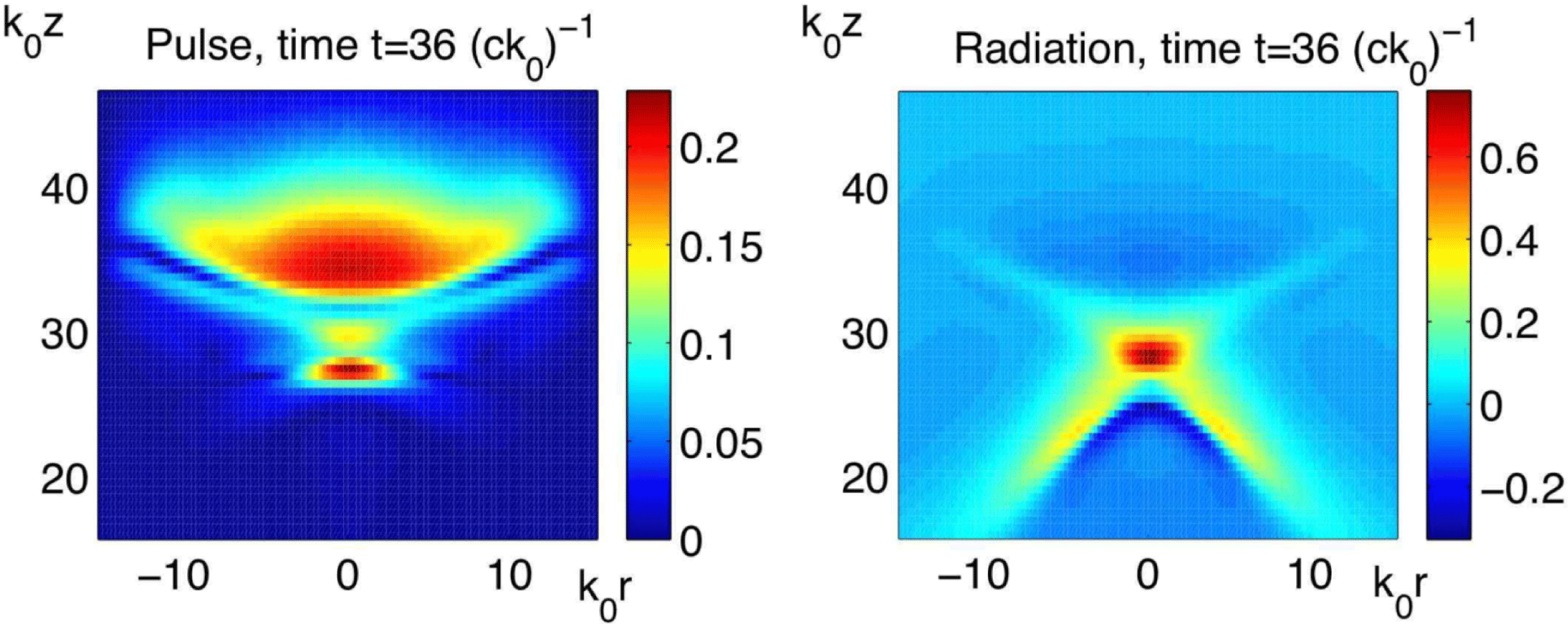
Figure 11. Cerenkov-like radiation (right) generated by pulse collapse into photon bullets (left) against longitudinal ![]() $z$ and transverse
$z$ and transverse ![]() $r$ co-ordinates of an initially Gaussian pulse of central wavenumber
$r$ co-ordinates of an initially Gaussian pulse of central wavenumber ![]() $k_{0}$. Reproduced with permission[Reference Marklund, Brodin and Stenflo75].
$k_{0}$. Reproduced with permission[Reference Marklund, Brodin and Stenflo75].
4.4 Effects on probe pulse form
In addition to the effects on single photons, one can consider the consequence of real photon–photon scattering on the propagation of an ensemble of photons. A probe laser pulse can be understood as a superposition of photons with a range of frequencies and phases. From the study of nonlinear dispersive media, it is well known that a refractive index that depends on a probe’s intensity directly or indirectly can lead to pulse shape effects[Reference Moloney and Newell58]. In particular, for the interaction with vacuum, probe pulse effects can occur if the next-to-leading-order effect of a probe-dependent refractive index is taken into account.
Nonlinear phase shift is a term used to denote the relative difference in phases between parts of a probe beam that have experienced different vacuum refractive indices. For a constant refractive index, the relative phase difference compared to a unitary refractive index is:
where ![]() ${\it\omega}_{p}z$ is the phase over which
${\it\omega}_{p}z$ is the phase over which ![]() ${\it\delta}{\it\phi}$ has been accrued. For two counterpropagating initially monochromatic plane waves, with the envisaged ELI parameters of 800 nm wavelength,
${\it\delta}{\it\phi}$ has been accrued. For two counterpropagating initially monochromatic plane waves, with the envisaged ELI parameters of 800 nm wavelength, ![]() $10^{25}~\text{W}~\text{cm}^{-2}$ intensity, 10 fs duration and
$10^{25}~\text{W}~\text{cm}^{-2}$ intensity, 10 fs duration and ![]() $10~{\rm\mu}\text{m}$ focal spot diameter, a phase shift of the order of
$10~{\rm\mu}\text{m}$ focal spot diameter, a phase shift of the order of ![]() ${\it\delta}{\it\phi}\approx 10^{-7}~\text{rad}$ has been calculated[Reference Ferrando, Michinel, Seco and Tommasini33, Reference Tommasini, Ferrando, Michinel and Seco70]. This nonlinear phase shift can be enhanced by using multiple crossings of the interacting beams. For
${\it\delta}{\it\phi}\approx 10^{-7}~\text{rad}$ has been calculated[Reference Ferrando, Michinel, Seco and Tommasini33, Reference Tommasini, Ferrando, Michinel and Seco70]. This nonlinear phase shift can be enhanced by using multiple crossings of the interacting beams. For ![]() $N_{r}$ reflections from plasma mirrors of reflectivity
$N_{r}$ reflections from plasma mirrors of reflectivity ![]() $R_{\text{mir}}$ of two beams crossing each other at an angle
$R_{\text{mir}}$ of two beams crossing each other at an angle ![]() ${\it\theta}_{c}$, the gain factor has been calculated to be[Reference Tommasini, Ferrando, Humberto and Seco71]:
${\it\theta}_{c}$, the gain factor has been calculated to be[Reference Tommasini, Ferrando, Humberto and Seco71]:
The measurement of this phase shift using Fourier imaging has also been explored[Reference Homma, Habs and Tajima72].
Vacuum self-focusing is an analogue to the well-known plasma self-focusing or ‘Benjamin–Weir’ instability[Reference Moloney and Newell58] in which there is positive feedback between a refractive index increasing the intensity of a pulse via focusing, and a higher intensity resulting from that focusing in turn increasing the refractive index. Mutual channelling of counterpropagating laser pulses and large-scale focusing have been considered, but either YW powers are predicted as necessary[Reference Rozanov66] or intensities above critical[Reference Fedotov73], before which vacuum pair-creation would have set in. In considering the idealized geometry of a Gaussian plane-wave probe pulse counterpropagating and interacting via six-wave mixing with a much slower varying pump, the probe-dependent refractive index:
was predicted to lead to the generation of a shock wave, a signature of self-focusing, when the phase difference due to the probe-dependent refractive index tended to a quarter wavelength[Reference Böhl, King and Ruhl34]. The mutual attraction between two photons due to mutual exchange of virtual photons on two vacuum loops has also been considered[Reference Kharzeev and Tuchin74], and a self-focusing angle of ![]() ${\it\theta}=\sqrt{157/16{\it\pi}^{3}}({\it\alpha}^{2}/180m^{4}R^{4})$ for photon separation
${\it\theta}=\sqrt{157/16{\it\pi}^{3}}({\it\alpha}^{2}/180m^{4}R^{4})$ for photon separation ![]() $R$.
$R$.
Pulse collapse is predicted to occur for high-intensity probe pulses propagating through an even higher-intensity background. The wave equation for the probe can be recast as a nonlinear Schrödinger equation[Reference Moloney and Newell58] with the consequence that the pulse envelope becomes space–time-dependent, even if assumed initially homogeneous. Unlike typical optically nonlinear dispersive media, the nonlinearity of the vacuum is ‘formed’ by the pump laser background, which is then probed by a second pulse. Even when the leading-order effect on the probe is a nonlinear refractive index that is independent of the probe pulse, because of its effect on the pump’s evolution, it can indirectly effect the probe’s propagation. This interplay between a Gaussian probe distribution propagating through a radiation gas has been demonstrated to lead to self-focusing and collapse of the probe into ‘photon bullets’, thereby driving acoustic waves[Reference Marklund, Brodin and Stenflo75] as demonstrated in Figure 11. Depending on initial parameters, probe collapse can occur before or after the critical Schwinger limit is reached[Reference Marklund, Eliasson and Shukla76].
4.5 Finite-time effects
Similar to the case for regular plasmas, there are effects on the probe when propagating through regions of the polarized ‘vacuum plasma’ that do not persist long enough to be directly detected.
Photon acceleration is well known from plasma physics[Reference Wilks, Dawson, Mori, Katsouleas and Jones77] and corresponds to the frequency downshift (upshift) as probe photons traverse an increasing (decreasing) plasma gradient. The possibility of measuring this effect in vacuum has been considered for a probe photon propagating almost parallel with a pump pulse[Reference Mendonca, Marklund, Shukla and Brodin78], with a frequency up (down) shift occurring at the rear (front) of the pump beam.
High-harmonic generation can also occur due to the inhomogeneity of the pump pulse background, in an effect distinct from standard vacuum high-harmonic generation. For a probe pulse counterpropagating with a slowly varying background, this is predicted to occur at finite time during overlap of the probe and pump pulses at an order earlier (via four-photon scattering), than for those photons that reach a detector (via six-photon scattering)[Reference King, Böhl and Ruhl79]. This finite-time signal disappears when the probe and pump pulses are well separated again, but is calculated to dominate the signal of frequency-shifted photons when the pulses overlap in this setup if ![]() $(E_{s}/E_{\text{cr}})^{2}{\it\omega}_{p}{\it\tau}_{s}\ll 1$ for strong-pulse duration
$(E_{s}/E_{\text{cr}})^{2}{\it\omega}_{p}{\it\tau}_{s}\ll 1$ for strong-pulse duration ![]() ${\it\tau}_{s}$.
${\it\tau}_{s}$.
Gradient-dependent vacuum refractive index is a way to describe the addition to the standard predicted vacuum refractive index that occurs when the pump laser is time varying. This has been calculated for a probe propagating through the electric/magnetic antinode of a pump standing wave[Reference Hu and Huang36]. The change in vacuum refractive index ![]() ${\rm\Delta}\mathsf{n}_{\text{vac}}$ can be written in the form:
${\rm\Delta}\mathsf{n}_{\text{vac}}$ can be written in the form:
In a setup of two colliding plane waves with no transverse structure, it was shown that this term is a surface term and is zero initially and finally, when the probe and background are well separated[Reference King, Böhl and Ruhl79]. The contact term was also noted in a recent study of polarization flipping in arbitrary plane waves[Reference Dinu, Heinzl, Ilderton, Marklund and Torgrimsson37]. Although it has been suggested that this part of the interaction could be a useful probe of dark matter particles[Reference Hu and Huang36], a consistent finite-time calculation has yet to be performed to establish the nature of this effect.
4.6 Nonperfect vacua
In any realistic experiment, the vacuum will be synthetic and hence imperfect. Residue particles in interaction chambers will also be affected by intense laser pulses and can produce a source of background that may obscure the measurement of real photon–photon scattering. The Cotton–Mouton effect, in which a dilute gas becomes birefringent in the presence of an electromagnetic wave is just one such example[Reference Zavattini, Gastaldi, Pengo, Ruoso, Della Valle and Milotti80]. In light of this, various proposals have been considered that instead use an altered vacuum to enhance the signal of vacuum polarization.
Resonant cavities can be employed in order to increase the sensitivity of whatever eigenfrequencies are resonant for that particular cavity[Reference Jackson48]. For example, a cavity can be designed such that the frequency that is generated by vacuum four-wave mixing of two modes of the cavity, is resonant. This idea has been studied for the ![]() $\text{TE}_{01}$ modes of such a cavity and the growth of the mixing signal in the form of the longitudinal standing-wave magnetic field, found to increase linearly with time[Reference Brodin, Marklund and Stenflo81] as
$\text{TE}_{01}$ modes of such a cavity and the growth of the mixing signal in the form of the longitudinal standing-wave magnetic field, found to increase linearly with time[Reference Brodin, Marklund and Stenflo81] as
for source magnetic standing-wave strengths ![]() $B_{1},B_{2}$ and coupling constant
$B_{1},B_{2}$ and coupling constant ![]() $V$. The vacuum signal was predicted to be detectable if an electric field
$V$. The vacuum signal was predicted to be detectable if an electric field ![]() $2\times 10^{-8}$ times the critical Schwinger field was employed with a superconducting cavity with a resistance of
$2\times 10^{-8}$ times the critical Schwinger field was employed with a superconducting cavity with a resistance of ![]() $1~\text{n}{\rm\Omega}$ and a resonant, vacuum-mixing frequency of
$1~\text{n}{\rm\Omega}$ and a resonant, vacuum-mixing frequency of ![]() $13.2~{\rm\mu}\text{eV}$. This idea was refined[Reference Eriksson, Brodin, Marklund and Stenflo82] and the prediction made that 18 photons can be produced by a magnetic field of around 0.28 T in a cylindrical cavity of length 2.5 m, radius 25 cm and quality factor
$13.2~{\rm\mu}\text{eV}$. This idea was refined[Reference Eriksson, Brodin, Marklund and Stenflo82] and the prediction made that 18 photons can be produced by a magnetic field of around 0.28 T in a cylindrical cavity of length 2.5 m, radius 25 cm and quality factor ![]() $4\times 10^{10}$.
$4\times 10^{10}$.
Real plasmas already have a refractive index different from unity, and this can combine with the shift of the refractive index due to vacuum polarization and lead to an enhancement. The system of equations by Akhiezer and Polovin[Reference Akhiezer and Polovin83] for the propagation of a circularly polarized plane wave through a cold collisionless plasma was updated to include the vacuum current in Maxwell’s equations and also take into account collisions[Reference Di Piazza, Hatsagortsyan and Keitel84]. For the collisionless case, the modified refractive index of the combined system was found to be:
with ![]() $\mathsf{n}_{\text{pl}}$ the plasma refractive index and
$\mathsf{n}_{\text{pl}}$ the plasma refractive index and ![]() ${\it\delta}\mathsf{n}_{\text{vac}}^{\bot }=\mathsf{n}_{\text{vac}}^{\bot }-1$ as defined in Equation (26). Another detectable signal of photon–photon scattering has been calculated to exist when an overdense plasma channel is subjected to an intense laser beam[Reference Shen, Yu and Wang85]. In addition, the altered dispersion relation for electromagnetic waves due to vacuum polarization effects in a strongly magnetized cold plasma has been calculated[Reference Brodin, Marklund, Stenflo and Shukla86–Reference Shukla and Stenflo88], which is particularly relevant for the dynamics of strongly magnetized neutron stars.
${\it\delta}\mathsf{n}_{\text{vac}}^{\bot }=\mathsf{n}_{\text{vac}}^{\bot }-1$ as defined in Equation (26). Another detectable signal of photon–photon scattering has been calculated to exist when an overdense plasma channel is subjected to an intense laser beam[Reference Shen, Yu and Wang85]. In addition, the altered dispersion relation for electromagnetic waves due to vacuum polarization effects in a strongly magnetized cold plasma has been calculated[Reference Brodin, Marklund, Stenflo and Shukla86–Reference Shukla and Stenflo88], which is particularly relevant for the dynamics of strongly magnetized neutron stars.
5 Summary
There has been a proliferation of labels to describe polarization effects of the quantum vacuum due to intense laser pulses. However, as we have discussed, all of these are manifestations of the QED prediction that real photons can scatter off one another. The commonality of the main approaches of describing real photon–photon scattering, through calculation of the polarization operator, scattering matrix elements and Heisenberg–Euler-modified Maxwell equations, has been made manifest. Many signals of this long-predicted phenomenon, whether at the level of individual photons or at the level of electromagnetic fields, have been calculated and found measurable in experiments using high-intensity laser pulses. This implies that the first measurement of real photon–photon scattering will finally be performed in the near future.













