1. Introduction
This review paper has been written with the assumption that the readers are primarily laser scientists who would like an overview of the various optimizations and design constraints for the laser that would be used in a laser fusion power plant.
In 1971–1972, scientists at Lawrence Livermore National Laboratory publicly proposed a new concept, called laser fusion, as a long-term option to generate electric power[Reference Nuckolls, Wood, Thiessen and Zimmerman1]. Their concept would repetitively launch small spherical targets of pure frozen deuterium–tritium (DT) into the middle of a large empty target chamber. The targets would be uniformly illuminated by multiple laser beams that would enter from holes in the chamber wall. The outer portion of the target, called the ablator, would be heated by the laser beams to produce a high temperature and high pressure plasma. The inner portion of the target, called the fuel, would stay Fermi-degenerate cold and be driven inwards by the high pressure of the rapidly expanding plasma ablator, as in a spherically imploding rocket. The cold fuel would then spherically compress to high densities. By carefully choosing the laser’s temporal pulse shape, a central portion of this compressed fuel would be heated to thermonuclear temperatures. This heated portion would ignite and produce a propagating burn through the surrounding cold compressed fuel, before the cold fuel could significantly expand. When repeated at several pulses per second, the thermonuclear burn would produce sufficient net power for an electric power plant. The neutron output would be absorbed in the chamber wall and partly converted to electricity. Some of the electricity would be sent to the external power grid, and some would be recirculated to produce more laser light. Some of the neutrons would be used to breed more tritium fuel and close the fuel cycle.
This concept was very attractive. There was no need for high magnetic fields to confine the plasma. The confinement was just the inertia of the compressed fuel. There would also be no need for an ultra-high vacuum in the target chamber, and the chamber walls would be far from the hot plasma for easier maintenance. The complex high-technology laser could even be located in a separate building, away from the radioactive environment, for easier maintenance.
The development costs can also be advantageous, if the program is properly structured. The laser consists of 40–60 or more identical beam lines. All of the laser development can be done on one beam line, which when perfected can then be duplicated. If testing shows that the target design needs to be modified, it is a small component of the total cost, and it can be modified while using the same laser system and chamber. Because the target chamber is basically a thick wall sphere, it would be relatively easy to change, modify, or replace compared to a magnetic fusion chamber with its complex intertwined magnets. Because this concept is modular and separable, optimization would be faster and not require a series of major investments.
There were four potential problems with the target performance in this fusion concept: (1) laser–plasma instabilities; (2) asymmetric laser illumination; (3) hydrodynamic instabilities during the shell implosion; and (4) insufficient target energy gain. It was soon discovered that solving these four problems was more challenging than had been originally expected. Now, after decades of research by a broad scientific community, and after various inventions and design changes, these four fundamental problems may all have been solved. There are still some uncertainties in the target physics that will be described below. However, the risk is now low enough, and the overall concept is attractive enough, that it is time to significantly increase the program level of effort. Then the remaining uncertainties in the target and the laser performance can be confronted, and perhaps resolved. If successful, the next step would address the remaining issues in the engineering, in fusion materials, and operational issues[Reference Obenschain, Sethian and Schmitt2]. This research device would then be followed by a prototype power plant.
A nice feature of the solutions of the above four problems is that the target design has been kept simple. The additional requirements are mostly in the laser system. The concept is still to use small spherical balls of nearly pure DT launched into the middle of a large empty chamber. It is the inherent simplicity of this fusion target which makes it so attractive as a long-term solution to the need for carbon-free electrical energy.
Why is target simplicity so important? First, because the plasma physics, the hydrodynamics, and the radiation flow all interact, and all have important physics in several time and/or space scales. Their behavior cannot be fully calculated, or even easily measured. Thus, adding physical complexity to the target, such as any type of non-symmetric target, adds to the risk of failure. Second, some types of geometric complexity (especially ‘indirect-drive’ targets) can reduce the coupling efficiency of the laser energy to the DT fuel. This would reduce the energy gain of the target, and thus the economic value of the system. Third, complex targets would cost more to manufacture. Fourth, complex targets with significant quantities of higher-
$Z$ material would increase the soft x-ray output and the debris from the target. This would make it difficult to design an inner surface of the chamber wall system that would survive the repetitive explosions, and would require recycling/processing of the high-
$Z$ target debris. Fifth, accelerating and placing complex targets into the chamber center would be an extra challenge. For example, an ‘indirect-drive’ target has a pellet delicately suspended inside the hohlraum, and care must be taken to ensure that the pellet neither breaks loose nor is off-center during the laser drive. The alternative ‘fast-ignition’ target would require precise angular alignment.
The solutions to the above target physics problems were instead mostly solved via a set of restrictions on the laser system. First, there was a shift to a higher laser frequency (shorter laser wavelength), from the infrared to the ultraviolet. This both reduced the risk of laser–plasma instabilities and increased the energy coupling efficiency[Reference Max3]. Second, optical beam smoothing (described below) was invented to produce a smooth and controllable laser profile[Reference Lehmberg and Obenschain4,Reference Skupsky, Short, Kessler, Craxton, Letzring and Soures5] . This not only reduced the asymmetry of illumination to acceptable levels; it also importantly reduced the risks of laser–plasma instabilities and of hydrodynamic implosion instabilities[Reference Obenschain, Grun, Herbst, Kearney, Manka, McLean, Mostovych, Stamper, Whitlock, Bodner, Gardner and Lehmberg6,Reference Mostovych, Obenschain, Gardner, Grun, Kearney, Manka, McLean and Pawley7] . Reducing the light scatter from the laser–plasma instabilities also increased the energy gain. The third and fourth changes were adjustments to the temporal profile of the laser pulse, producing separate early[Reference Metzler, Velikovich, Schmitt and Gardner8] and late[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov9] shocks. The early shock tuned the radial isentrope of the target. This tuning significantly reduced the growth of hydrodynamic implosion instabilities. With a late shock, the heating of the ignition region could be separated from the compression of the cold main fuel. This provides significantly higher energy gains, albeit with some higher risk from laser–plasma instabilities, as explored below. These various laser changes will be discussed below.
2. Target design
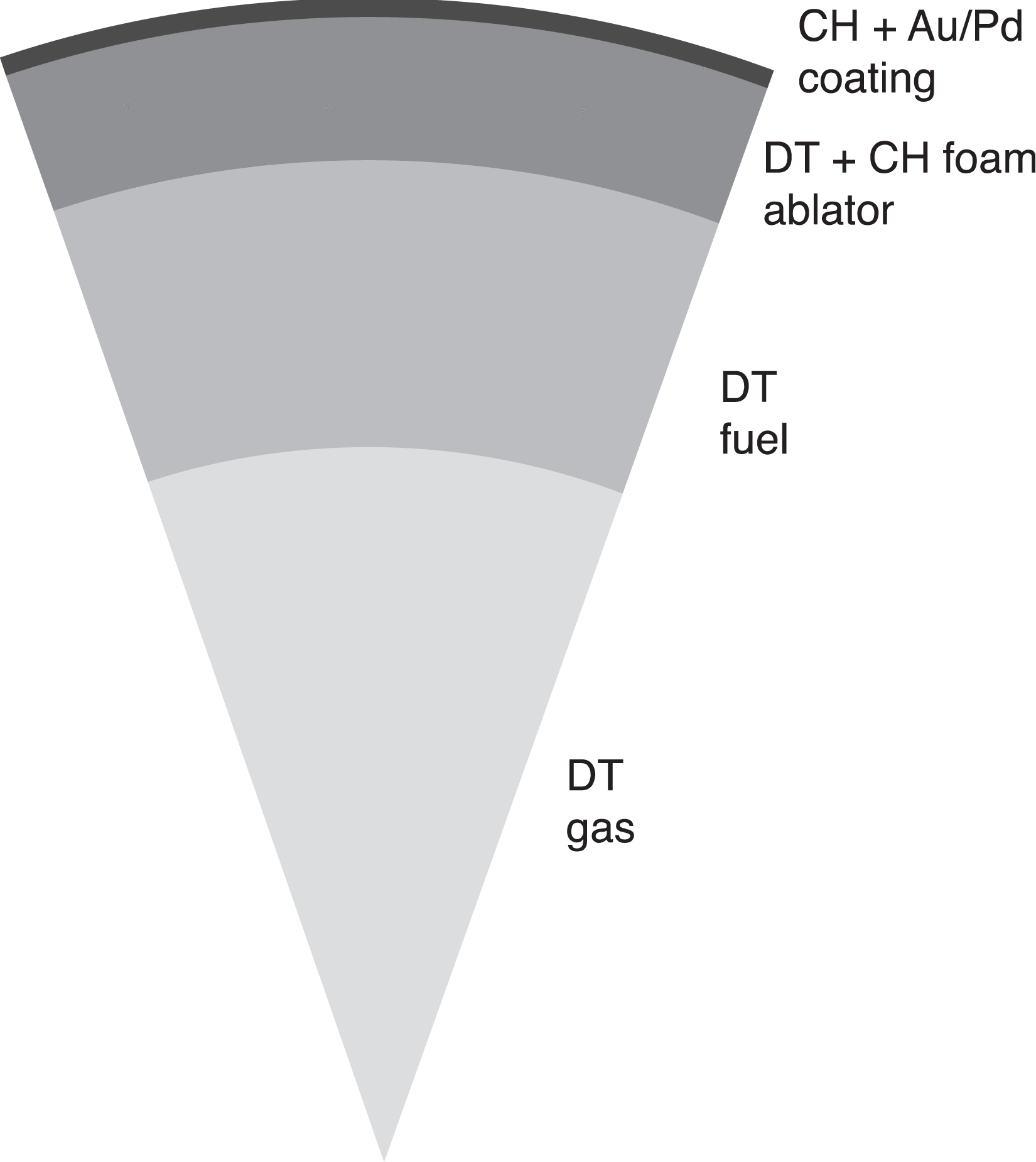
Figure 1 shows a conical section of a modern spherical target design. There are four physical regions. The frozen DT fuel layer is surrounded by an ablator that is still mostly DT, but is now embedded in a low-density CH foam. Various designs have foam densities of 40–100 
$\mathrm{mg} / {\mathrm{cm} }^{3} $. Surrounding the ablator is a thin coating of CH, 1–5 
$\mathrm{\mu} \mathrm{m} $ thick, and then a very thin coating of Pd or Au/Pd; approximately 0.1 
$\mathrm{\mu} \mathrm{m} $ thick. The CH layer provides a base to deposit the Au/Pd coating, and it also seals in evaporating DT gas from the DT. The Au/Pd coating protects the target from preheating by the infrared radiation from the chamber wall, and it also helps reduce the imprinting of laser nonuniformities on to the target[Reference Obenschain, Colombant, Karasik, Pawley, Serlin, Schmitt, Weaver, Gardner, Phillips, Aglitskiy, Chan, Dahlburg and Klapisch10]. The use of the Au/Pd alloy rather than pure Au allows for relatively fast filling of the target with DT. Pure Au is virtually impervious to DT. The high required infrared reflectivity and rapid permeation of the Au/Pd alloy have been demonstrated[Reference Stephens11].
Inside the frozen DT fuel shell there is DT gas, in equilibrium with the frozen DT. Except for the addition of the low-density CH foam and the thin CH and Au/Pd coatings, the target is still mostly DT, as in the 1971–1972 target concept. The specific dimensions of each layer depend upon the laser energy and wavelength, the target smoothness, and on various other optimizations that are chosen to minimize the risks of laser–plasma and hydrodynamic instabilities. As an example, with a 0.5 MJ laser the total target radius is approximately 1 mm.
Figure 1. Section of generic high-gain laser fusion spherical target design.
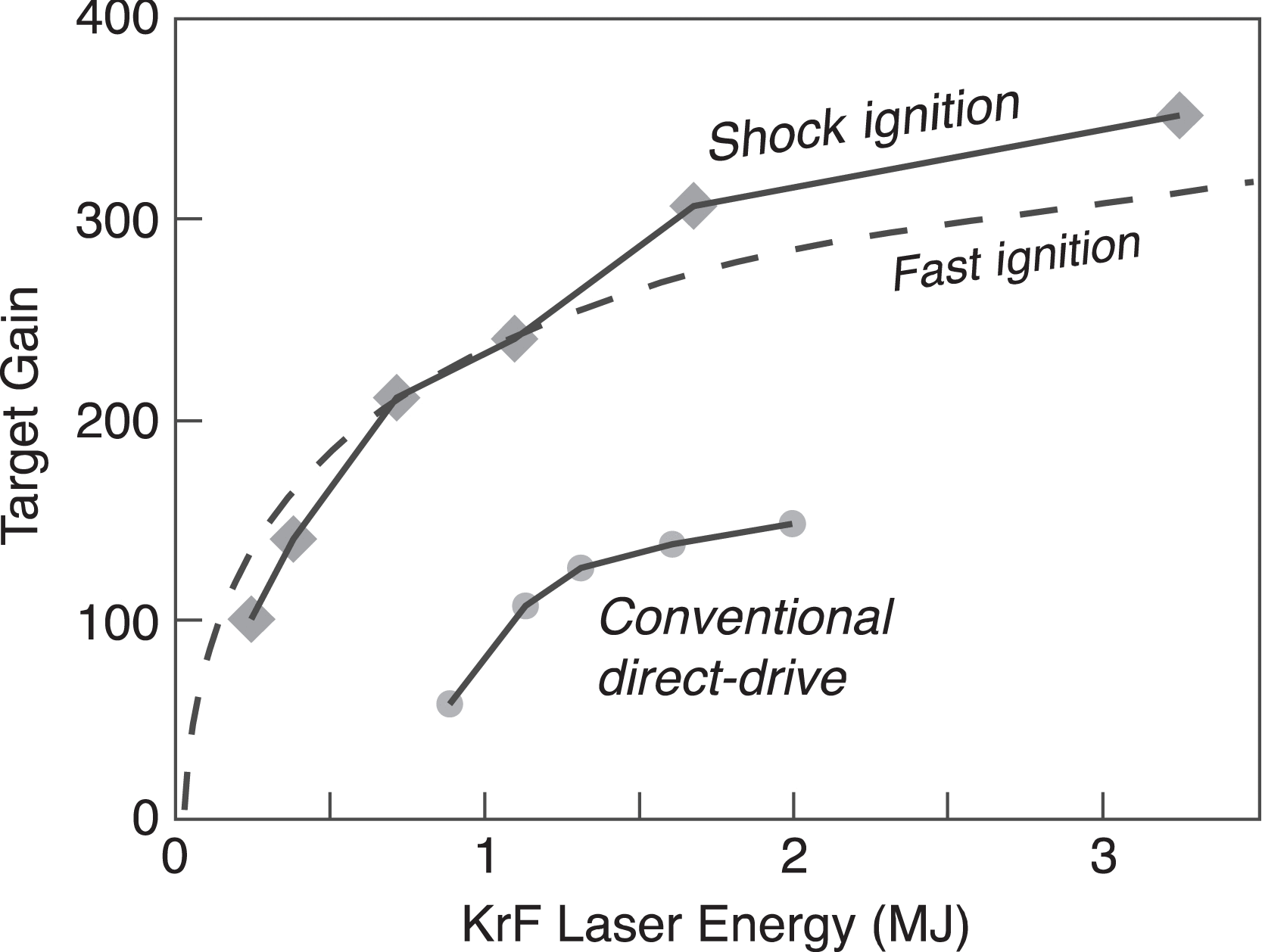
This modern target can operate in different physical modes[Reference Schmitt, Colombant, Velikovich, Zalesak, Gardner, Fyfe and Metzler12]. Predicted optimum energy gains for two of these modes, the ‘shock-ignition’ and ‘conventional’ designs, with a KrF (krypton fluoride) laser, are shown in Figure 2. Also shown is an optimum calculation for the geometrically complex ‘fast-ignition’ target design. The fast-ignition target concept will not be discussed here because it has no energy gain advantage over the simpler, purely spherical, shock-ignition target, and it has the disadvantages of greater target complexity and physics risk, and the need for a second laser system for ignition. All of these calculations were performed with the same detailed computer model.
Figure 2. Predicted target energy gains versus incident laser energy for several designs. Shock-ignition gains are similar to fast-ignition target gains, and KrF lasers have superior performance due to their shorter laser wavelength and the ability to reduce the focal spot size to match the imploding target.
To compare target performance using a DPSSL (diode-pumped solid-state laser) instead of a KrF laser, it is important to use the same computer target design code, with the same physics, and to determine which physical parameters to vary and which to hold fixed. For a fair comparison, the DPSSL laser pulse shape was adjusted to produce as closely as possible the same drive pressure as the KrF laser. This should produce other physical parameters (compressed areal mass, shock timing, adiabat, and pellet yield) that are as similar as possible. The KrF design utilizes optical ‘zooming’ in which the focal spot size is reduced during the implosion to minimize refractive losses. Zooming is difficult and costly with a DPSSL, but not impossible. Thus two calculations were performed for the DPSSL, with and without zooming. The results are shown in Table 1 using a target design with shock ignition.
Table 1. Comparison of target performances for a shock-ignition target driven by the two types of laser, with the same ablation pressure, and similar fuel mass and thermonuclear yields. For the DPSSL, with its poorer laser–target coupling, the target energy gain drops significantly and the possible deleterious effects of laser–plasma instabilities increase significantly
The penalty for using this slightly longer wavelength laser can be considerable. Even if zooming is invoked, almost twice as much laser energy is required at the 
$0. 35~\mathrm{\mu} \mathrm{m} $ wavelength. Almost three times as much energy is needed without zooming. The energy gain for this target drops from 97 with KrF to 56 and 35 for the DPSSL. (This difference can be lessened somewhat if the absorption of the 
$0. 35~\mathrm{\mu} \mathrm{m} $ light can be increased, for example, by using more collisional ablators. However, such changes can lead to higher risk of hydrodynamic instability due to thinner shells and lower drive pressure.) Another disadvantage is the higher maximum laser intensity needed to produce the same drive pressure. When the laser intensity is above the laser–plasma instability threshold, problems can be roughly estimated by the ratio of the light pressure to the plasma pressure, 
${\sim }I{\lambda }^{2} / P$, where 
$I$ is the intensity and 
$\lambda $ is the laser wavelength. This product is significantly higher for the DPSSL designs. Although all of the laser–plasma coupling physics strongly favors a KrF laser over a DPSSL, it is premature to make a down selection. There are many other factors that will have to also be evaluated to determine the optimum laser for a fusion power plant.
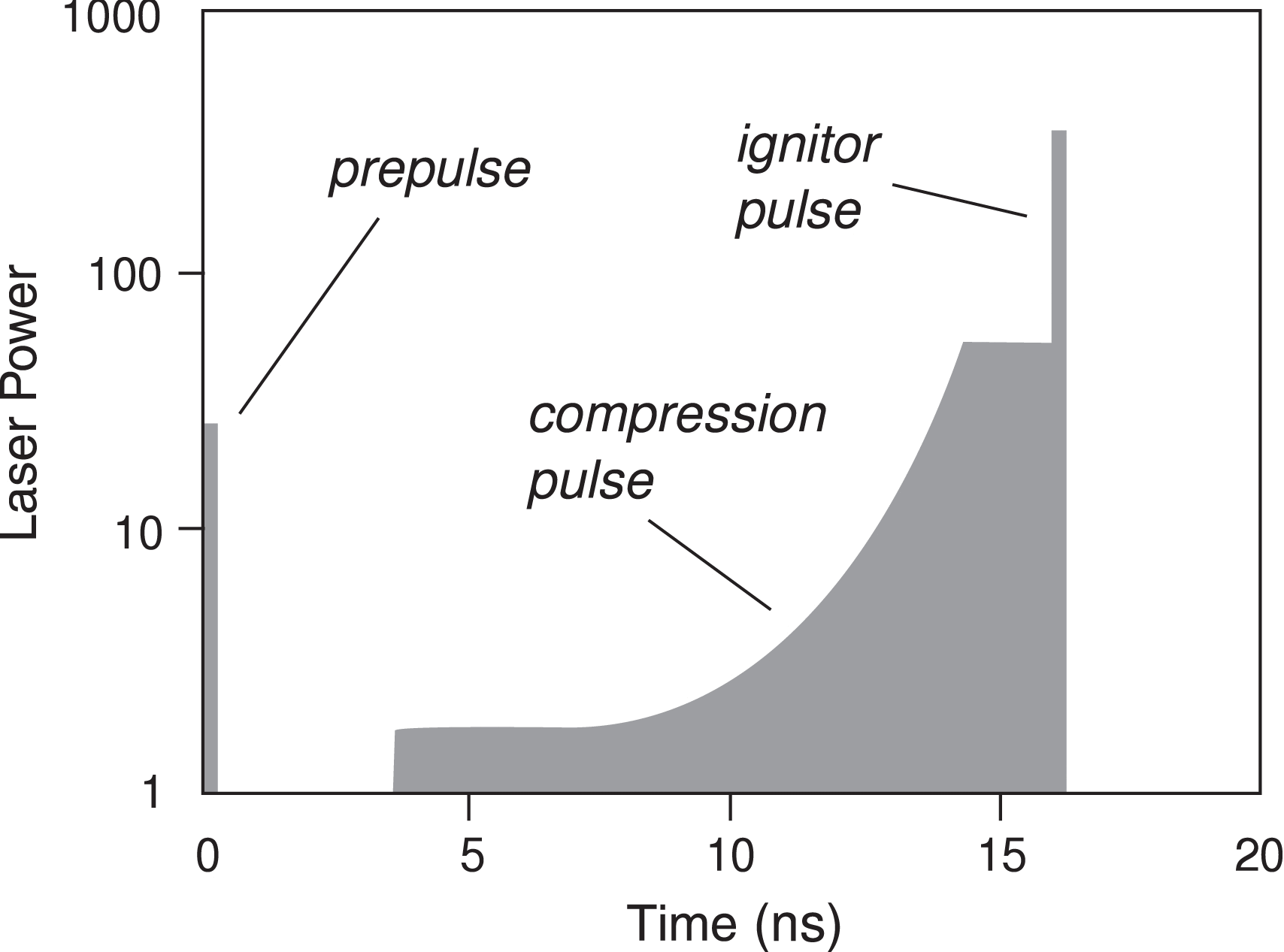
Typical laser pulse shapes are shown in Figure 3. There is a short initial laser prepulse, approximately 0.1 ns in width, that is used to set the initial radial profile of the ablator adiabat. This adiabat shaping reduces the growth of the hydrodynamic instabilities. Then there is the main laser pulse, beginning with a sharp increase, followed by a tuned increase in power that isentropically compresses the DT fuel. For the highest gain ‘shock-ignition’ design, the compression power is less, and there is a third final sudden increase in laser power, used to ignite the central portion of the compressed fuel. The dynamic range in the laser power is generally a factor of a few hundred.
Figure 3. Generic laser pulse shape for the shock-ignition target. The prepulse sets the initial radial adiabat. The main pulse compresses the cold fuel. The ignitor pulse produces the spark for ignition. The conventional direct-drive target pulse shape is similar except without the final ignitor pulse.
Figure 4. Naval Research Laboratory’s electron beam pumped Electra KrF laser system. The laser output window is between the two black magnet coils in the center of the photo. The arrow shows the laser path. The magnets guide the electron beams into the laser gas. The pulsed power systems for the electron beams consist of the blue pulse forming lines and the two white tanks that flank the laser cell.
A long list of possible laser–plasma instabilities has been investigated[Reference Kruer13]. For a purely spherical target with direct illumination, using a short laser wavelength, and with optical beam smoothing, several of these instabilities are not important during the compression of the DT fuel. Either their laser intensity threshold is too high (they are stabilized by plasma density and velocity gradients), or they are stabilized by the use of optical beam smoothing.
There are two laser–plasma interactions that could possibly be a problem for spherical targets with direct illumination. Their risk in still uncertain.
The first concern is the two-plasmon decay instability. This mode transfers some of the laser energy into two electron plasma waves: 
${\omega }_{L} \rightarrow 2{\omega }_{pe} $. The plasma waves then produce suprathermal electrons that can preheat the cold DT fuel and prevent sufficient compression. The higher performance (shock-ignition) target designs require a laser intensity that is a few times the threshold value at the end of the compression pulse. The laser intensity threshold is well known, and compares well with experimental measurements. However, the behavior of this instability when above its threshold value is a very complex problem, because of the multiple time scales and space scales in the physics. After extensive efforts by several research groups, theory and modeling still disagree with experimental measurements. A full test of this instability in the physical regime of the target designs will have to await a test with larger laser facilities than are currently available. The final ignitor pulse is well above instability threshold, but preheating from suprathermal electrons in this part of the pulse is not expected to be dangerous[Reference Perkins, Betti, LaFortune and Williams14] unless the suprathermal electron energy exceeds 100–150 keV.
The second concern is called cross-beam energy transfer (CBET)[Reference Igumenshchev, Seka, Edgell, Michel, Froula, Goncharov, Craxton, Divol, Epstein, Follett, Kelly, Kosc, Maximov, McCrory, Meyerhofer, Michel, Myatt, Sangster, Shvydky, Skupsky and Stoeckl15], which can also be viewed as seeded stimulated Brillouin scattering. When two laser beams cross at an angle in the plasma, their interference pattern will produce an ion acoustic wave. This ion acoustic wave then acts like a Bragg crystal and can scatter laser energy from one of the laser beams to the other. This transfer would induce illumination asymmetry and therefore prevent sufficient spherical convergence. The laser intensity threshold for this instability is low, and all of the target designs are susceptible. A full evaluation of this instability will also require a larger laser system.
There are techniques that may control these two laser–plasma instabilities so that they would not prevent a successful implosion. Control would use a combination of a short laser wavelength and a broad laser bandwidth with beam smoothing. These techniques will be discussed further in Section 3.
3. Laser requirements
Laser wavelength
When laser light propagates in a plasma, the dielectric constant is given by 
$\varepsilon = 1- { \omega }_{pe}^{2} / { \omega }_{L}^{2} $, where 
${\omega }_{pe} $ is the plasma frequency and 
${\omega }_{L} $ is the laser frequency. The dielectric constant in a plasma is thus less than 1. Since 
${ \omega }_{pe}^{2} $ is proportional to the plasma density, we can define 
${ \omega }_{L}^{2} \approx {n}_{c} $ and rewrite the dielectric constant 
$\varepsilon = 1- n/ {n}_{c} $. The quantity 
${n}_{c} $ is called the ‘critical density’. It is the maximum plasma density where light can penetrate, and its value varies as the square of the laser frequency.
Laser light is absorbed in the plasma by electron–ion collisions. With a higher frequency laser, the light can penetrate into higher plasma densities. Absorption of the laser power at a higher plasma density implies a lower plasma temperature. The combination of higher density and lower temperature leads to a higher percentage of light absorption, and a lower percentage of refractive losses. It also implies a higher ablation pressure. Therefore, to implode the same amount of DT fuel with the same pressure, one would need less laser energy when using a shorter wavelength. This implies a higher energy gain.
When the laser fusion concept was first proposed, the thought was to use infrared laser light. However, this long laser wavelength excited plasma instabilities near the critical density. By shifting from 1 
$\mathrm{\mu} \mathrm{m} $ to 
$1/ 3~\mathrm{\mu} \mathrm{m} $ or 
$1/ 4~\mathrm{\mu} \mathrm{m} $ light, the critical density increased by a factor of 9 or 16. With the increased collisional light absorption, negligible laser light reaches the critical density and the instabilities there were eliminated. However, even the small wavelength decrease from 
$1/ 3~\mathrm{\mu} \mathrm{m} $ to 
$1/ 4~\mathrm{\mu} \mathrm{m} $ increases the critical density by almost a factor of 2, and leads to a substantial improvement in performance, as shown in Table 1.
There is a second advantage to a higher laser frequency that is even more important: the control of laser–plasma instabilities in the underdense plasma. The ponderomotive force driving these instabilities decreases, and the plasma pressure resisting the force increases, as the frequency increases. Also, since higher laser frequencies couple to the plasma at a higher density, there is more collisional damping. The net effect is that the laser intensity threshold for many of these instabilities increases linearly with the laser frequency.
The third basic advantage of a shorter laser wavelength is an increase in the mass ablation rate. The growth rate of the Rayleigh–Taylor hydrodynamic instability is reduced by mass ablation, as the unstable fluid waves are convected away from the ablation interface. Shortening the laser wavelength increases the mass ablation rate, and this reduces the Rayleigh–Taylor growth rate.
Laser beam smoothing and broad bandwidth
At the beginning of the laser fusion program there was one major advantage to the use of an infrared laser wavelength. Large laser systems all have inherent phase distortions, which produce unacceptable intensity hot spots at the focus; the peak-to-average intensity ratio is typically 10 to 1. To produce a stable and symmetric implosion, the pressure nonuniformity has to be reduced a factor of 1000, to about 1%. In the original concept, sideways thermal conduction in the plasma corona surrounding the target would smooth out the pressure nonuniformity. Depositing the laser energy at a sufficiently low density, so that there would be a sufficiently thick plasma corona for thermal smoothing, requires infrared lasers. For many years there was a fundamental conflict in the direct-illumination fusion concept. Control of laser–plasma instabilities required a short laser wavelength, while control of the laser nonuniformity required a long laser wavelength.
This conflict was finally resolved with the invention of optical smoothing techniques: first induced spatial incoherence (ISI)[Reference Max3] and then smoothing by spectral dispersion (SSD)[Reference Lehmberg and Obenschain4]. Both techniques, using different methods, break up the laser beam into many small transverse beamlets, each of which has minimal phase distortion and is thus nearly ideal. ISI is best matched to a KrF gas laser, while SSD is best matched to a solid-state laser such as the DPSSL. The interference pattern at the focus of the beam, produced by the overlap of the numerous beamlets, can rapidly change if there is a broad laser bandwidth. The time-averaged intensity nonuniformity is then approximately 
$ \mathrm{\Delta} I/ I\approx \sqrt{0. 67/ \mathrm{\Delta} {\nu }_{L} t} $, where 
$t$ is the averaging time and 
$ \mathrm{\Delta} {\nu }_{L} $ is the frequency bandwidth. If the hydrodynamic plasma response time is 1 ns, and the laser frequency bandwidth is 3 THz, then the time-averaged intensity nonuniformity is less than 1.5%. When combined with the residual thermal smoothing, computer simulations indicate that the laser imprinting can be reduced to an acceptable level.
A KrF gas laser can produce a bandwidth of 3 THz. It has been shown on the Omega laser that 1.0 THz can be obtained at the third-harmonic. DPSSLs can also be designed with a crystalline lasing medium instead of glass. Crystals are attractive for a DPSSL power plant because they have a higher inherent laser efficiency, but have much less bandwidth than glass. Overlapping many laser beams, each with a different central frequency, is not geometrically or physically equivalent to a single laser beam with a broad laser bandwidth.
The two optical smoothing techniques, ISI and SSD, are fundamentally different in the way they work, yet their impacts on the target are very similar, if the bandwidth is the same. There are however a few differences that may be important. ISI creates statistically independent beamlets, and their overlapping interference pattern is truly random. SSD however creates a periodic modulation, and there is some residual interference pattern even with time averaging, especially in the longest transverse modes that approach the overall focal spot size.
During most of the laser pulse, there is a plasma corona that provides some additional thermal smoothing of the residual laser nonuniformities. However, when there is a rapid increase in the laser intensity, then the plasma corona is not in equilibrium with the laser intensity and the target is most vulnerable to laser imprinting. This rapid change occurs during the initial short prepulse; again at the beginning of the compression pulse; and again during the final ignitor pulse that is used with the ‘shock-ignition’ target. Thus the safest strategy would be to maintain the broadest possible laser bandwidth during the entire laser pulse. If there is insufficient laser bandwidth, and the target fails to ignite, any other optimization parameter becomes irrelevant.
A large 
$ \mathrm{\Delta} {\nu }_{L} $ is useful for other purposes than beam smoothing. The various laser–plasma instabilities can be reduced when 
$ \mathrm{\Delta} {\nu }_{L} \geq \gamma $, where 
$\gamma $ is the growth rate of an instability. The easiest instability to control is the filamentation mode. In this instability, the plasma density within the hot spots of the laser beam is reduced, either by local laser heating or by the light’s ponderomotive force. The lower plasma density increases the dielectric constant 
$\varepsilon $, and this self-focuses the laser beam. However, if the hot spots in the laser beam move before the plasma can respond, then the self-focusing will be prevented. This requires a laser bandwidth of 0.1–1 THz. Control of the filamentation mode has been demonstrated experimentally and explained with detailed computer modeling[Reference Schmitt16].
Beam smoothing may also have a positive impact on cross-beam energy transfer, although it has not yet been experimentally demonstrated. As in the case of stimulated Brillouin scattering[Reference Mostovych, Obenschain, Gardner, Grun, Kearney, Manka, McLean and Pawley7], if the laser bandwidth exceeds the acoustic frequency of the beating between the laser beams, then the acoustic waves should not fully develop.
There is a similar potential, also not yet demonstrated, for the two-plasmon decay instability. If the laser bandwidth exceeds the growth rate of this instability, then the instability should not develop. This stabilization is most likely when the instability is near its laser intensity threshold value and the growth rate is minimal. This provides to other reason to use a KrF laser: both a larger laser bandwidth and a target design that is closer to the instability threshold.
There is one other nice advantage of optical beam smoothing[Reference Lehmberg and Goldhar17], called ‘optical zooming’. Because ISI is an optical relay system, the focal spot size can be modified by changing the aperture size at the oscillator. This is simple to do several times during the laser pulse, using a set of partially reflecting mirrors and optical switches. Thus, as the spherical target decreases in size, the laser focal spot size can be reduced in a series of steps to match the target. This reduces the laser refractive losses, minimizes any cross-beam transfer, increases the collisional absorption, and significantly increases the target gain. Energy gain improvements of about 30% are predicted. Zooming has been demonstrated with the KrF laser[Reference Kehne, Karasik, Aglitsky, Smyth, Terrell, Weaver, Chan, Lehmberg and Obenschain18].
With SSD, the optical smoothing technique used with glass lasers, optical zooming is more difficult, since SSD is not an optical imaging system. One could devote different spatial sections of each laser beam to different temporal components of the laser pulse, but that would require double or triple the cross-sectional area of the optics and thus add significant capital cost.
Laser intensity
If the best current fusion target designs are slightly above threshold for a laser–plasma instability, then the following question naturally arises: why not simply adjust the target design by lowering the laser intensity? This can be most easily explained using the relation 
${V}^{2} = 2as$. There is a similar equation in spherical geometry, which can quickly be obtained by replacing the distance 
$s$ with the radius 
$R$, and the acceleration 
$a$ with 
$P/ (\rho \mathrm{\Delta} R)$. Then the equation becomes
$${V}^{2} \sim \frac{P(I, \lambda )}{\rho } \frac{R}{ \mathrm{\Delta} R} .$$ Reducing the laser intensity 
$I$ will reduce the ablation pressure 
$P$. To achieve the same implosion velocity then requires an increase in the shell’s aspect ratio, 
$R/ \mathrm{\Delta} R$. The problem is that thinner shells are more susceptible to breakup by the hydrodynamic instabilities such as the Rayleigh–Taylor mode. The peak laser intensity is thus limited from below by hydrodynamic instabilities and from above by laser–plasma instabilities.
Laser spatial profile
Optical beam smoothing can reduce the nonuniformities in each laser beam to an acceptable level. But that only addresses the high-mode spherical nonuniformities. Can a finite number of even perfect laser beams produce sufficiently low-mode symmetric illumination on a sphere?
The short explanation is to imagine a spherical coordinate system with its origin at the center of the spherical target, and imagine then a single laser beam with uniform intensity that is propagating inward along the 
$z$-axis. The intensity profile on the surface of a hard sphere will be a cosine function, in polar coordinates. Now imagine that the intensity profile of the laser beam is also a cosine function, in the same coordinate system. The profile on the sphere is now a 
${\mathrm{cosine} }^{2} $. We know from our basic geometry that a set of 
${\mathrm{cosine} }^{2} $ sometimes add up to unity. And indeed, one can produce perfectly uniform illumination on a sphere with as few as six laser beams[Reference Schmitt19]. In practice many more laser beams are necessary, typically 40–60, because the laser intensity profile will typically be a hypergaussian, not a cosine; because there are refractive effects in the plasma corona; because the beams will be slightly misaligned; and because they will have slightly different energies. In practice, it appears that about 60 laser beams should suffice[Reference McGeoch20]. Further analysis is warranted.
Laser pulse shaping
Glass laser media have a long inversion time and they are thus a good energy storage system for lasing. One can easily calculate the effects of saturation on the pulse shape and construct the temporal shape at the oscillator that will produce the desired profile at the end of the laser chain. With careful tuning, one can produce pulses with the required dynamic range of about 100.
However, the KrF excited-state molecule has an inversion time of only a few nanoseconds, and it is not a good storage system. The lasing medium has a high-gain coefficient and must be optically loaded continuously to keep it from self-oscillating. The laser also operates most efficiently in large systems when it is pumped by electron beams for a fraction of a microsecond, much longer than the inversion time. The required output pulse, with pulse shaping, is obtained by putting a consecutive series of pulses through the amplifiers at slightly different angles and times, and then restacking them to simultaneously arrive at the fusion target[Reference Hanlon and McLeod21]. For example, if the desired laser pulse has a high-power duration of 3.5 ns, and a total duration of 15 ns, then one would send a series of pulses through the laser amplifier at slightly different angles, separated by 3.5 ns[Reference Lehmberg, Giuliani and Schmitt22]. There are advantages and disadvantages to this type of system, and its optical design is very different from the more common solid-state laser. Both the optical concept and the pulsed power pumping system were originally thought by some to be too impractical, but full success has been demonstrated on the Nike laser system. Complex temporal pulse shapes, pulse stacking, and a reliable gas laser with a pulsed power system have all been shown to be feasible and practical.
Laser repetition rate
For any fixed laser energy output per pulse, and fixed chamber diameter, the cost of electricity would be minimized by operating at the highest possible repetition rate. This repetition rate is probably limited by the ability to clear debris from the chamber and to remove waste heat from the laser. The current assumption is that the repetition rate will be five to ten pulses per second.
Laser reliability
Five pulses per second equals 158 million shots per year. To minimize down-time and maintenance costs, it would be desirable for the laser and the target chamber to operate five years between major maintenance. However that does not now seem realistic. We recommend a goal of one year, or about 150 million shots between major maintenance.
Laser efficiency and capital costs
To produce electricity at an attractive cost, a reasonable assumption has been 
$\eta G\geq 10$, where 
$\eta $ is the laser wall plug efficiency, and 
$G$ is the target energy gain. The product of the two determines the fraction of the electricity generated that has to be recycled for the next laser shot, and thus the capital costs. Neither parameter by itself determines the optimal design. The product 10 limits the fraction of electrical energy that has to be recycled to about one-fourth. A detailed study[Reference Sethian, Colombant, Giuliani, Lehmberg, Myers, Obenschain, Schmitt, Weaver, Wolford, Hegeler, Friedman, Robson, Bayramian, Caird, Ebbers, Latkowski, Hogan, Meier, Perkins, Schaffers, Kahlik, Schoonover, Sadowski, Boehm, Carlson, Pulsifer, Najmabadi, Raffray, Tillack, Kulcinski, Blanchard, Heltemes, Ibrahim, Marriott, Moses, Radell, Sawan, Santarius, Sviatoslavsky, Zenobia, Ghoniem, Sharafat, El-Awady, Hu, Duty, Leonard, Romanoski, Snead, Zinkle, Gentile, Parsells, Prinksi, Kozub, Dodson, Rose, Renk, Olson, Alexander, Bozek, Flint, Goodin, Hund, Paguio, Petzoldt, Schroen, Sheliak, Bernat, Bittner, Karnes, Petta, Streit, Geller, Hoffer, McGeoch, Glidden, Sanders, Weidenheimer, Morton, Smith, Bobecia, Harding, Lehecka, Gilliam, Gidcumb, Forsythe, Parikh, O’Dell and Gorensek23], as part of the US High Average Power Laser program, estimated that the net wall plug efficiency of a KrF laser would be approximately 7%, and thus the minimum target gain is approximately 140.
As part of the US High Average Power Laser program, the Mercury DPSSL achieved an efficiency of 5% at the fundamental laser wavelength of 
$1~\mathrm{\mu} \mathrm{m} $. There has been a recent design study[Reference Erlandson, Aceves, Bayramian, Bullington, Beach, Boley, Caird, Deri, Dunne, Flowers, Henesian, Manes, Moses, Rana, Schaffers, Spaeth, Stolz and Telford24] for a DPSSL that estimates the wall plug efficiency for a fusion energy laser driver could be as high as 16%, using diodes that are 72% efficient[Reference Deri, Geske, Kanshar, Patterson, Kim, Hartmann, Leibreich, Deichsel, Ungar, Thiagarajan, Martinsen, Leisher, Stephens, Harrison, Ghosh, Rabot and Kohl25]. These efficiencies have not yet been demonstrated and would require advances in several technologies.
One interesting reactor scenario, using a KrF laser with a shock-ignition target, and assuming some degradation from the predicted 1D target performance in Figure 2, would have the following parameters.
KrF laser energy: 0.7 MJ
Repetition rate: 5 pps
KrF laser efficiency: 
$\eta = 7\% $
Target energy gain: 
$G= 150$
Blanket burnup gain 
$\beta = 1. 1$
$\eta G= 10. 5$ and 
$\beta \eta G= 11. 5$
Thermal to electric conversion: 40%
Total electrical power output: 231 MWe
Recirculated electricity for the laser: 50 MWe
Power to the grid: 181 MWe (minus auxiliary plant requirements)
Cost per DT target[Reference Goodin, Alexander, Brown, Frey, Gallix, Gibson, Maxwell, Nobile, Olson, Petzoldt, Raffray, Rochau, Schroen, Tillack, Rickman and Vermillion26]: $0.15
There are various advantages to this modest-sized 181 MWe power plant, versus the few-thousand MWe typically proposed for a magnetic fusion power plant. (1) A lower total investment to develop and test the concept, combined with the lower development costs associated with developing a modular separable system. (2) A lower initial investment by industry as they evaluate the lifetime costs of this new technology. (3) Less reduction of peak electrical power output during shut downs of individual units. (4) More rapid construction times.
Status of KrF laser drivers
Development of electron beam pumped KrF lasers for IFE has been carried out both on Electra and Nike lasers at NRL. Nike is a 3000–5000 J single-pulse system that has been used to develop large-area electron beams at a size comparable to that envisioned for a full-scale reactor-grade amplifier. Electra is a 700 J laser that is being used to develop technologies that can meet the fusion energy requirements for rep-rate, efficiency, durability, and cost. The technologies developed on Electra are scalable to a full-scale (15–30 kJ) amplifier. A photo of Electra appears in Figure 4.
Nike is the world’s largest KrF laser. It produces 2–3 kJ of laser light on target in routine operation. The laser beam has very high quality illumination on target (time-averaged nonuniformity 
${\lt }0. 3\% $), and very high bandwidth (up to 3 THz). As discussed earlier, Nike has demonstrated zooming by means of an optical switchyard that progressively routes the laser through decreasing apertures. The switchyard is located in the low-energy front-end of the laser.
The Electra KrF laser runs at 2.5–5 Hz and produces between 300 and 700 J per pulse in an oscillator mode. Based on experimental results with the individual components, a fusion energy class KrF laser is predicted to have a wall plug to laser light on target efficiency in excess of 7%[Reference Sethian, Colombant, Giuliani, Lehmberg, Myers, Obenschain, Schmitt, Weaver, Wolford, Hegeler, Friedman, Robson, Bayramian, Caird, Ebbers, Latkowski, Hogan, Meier, Perkins, Schaffers, Kahlik, Schoonover, Sadowski, Boehm, Carlson, Pulsifer, Najmabadi, Raffray, Tillack, Kulcinski, Blanchard, Heltemes, Ibrahim, Marriott, Moses, Radell, Sawan, Santarius, Sviatoslavsky, Zenobia, Ghoniem, Sharafat, El-Awady, Hu, Duty, Leonard, Romanoski, Snead, Zinkle, Gentile, Parsells, Prinksi, Kozub, Dodson, Rose, Renk, Olson, Alexander, Bozek, Flint, Goodin, Hund, Paguio, Petzoldt, Schroen, Sheliak, Bernat, Bittner, Karnes, Petta, Streit, Geller, Hoffer, McGeoch, Glidden, Sanders, Weidenheimer, Morton, Smith, Bobecia, Harding, Lehecka, Gilliam, Gidcumb, Forsythe, Parikh, O’Dell and Gorensek23,Reference Burns, Myers, Sethian, Wolford, Giuliani, Lehmberg, Friedman, Hegeler, Jaynes, Abdel-Khalik, Sadowski and Schoonover27] . Confidence in this efficiency prediction is based on advances in the electron beam generation, transport, and gas deposition, the pulsed power, the thermal management and established KrF physics. A method has been developed to cool the electron beam transmission windows (foils) by injecting cold laser gas directly onto the foil[Reference Lu, Abdel-Khalik, Sadowski and Schoonover28]. This method keeps the foils well below the long-term cyclic fatigue temperature, maintains the high quality laser focal profile, and requires minimal power consumption.
Electra has run continuously as a laser for 10 hours at 2.5 Hz. It has also run for 50,000 pulses in two contiguous runs at 5 Hz (a total of 2 hours and 47 minutes). Over 320,000 laser pulses were taken in an 8-day period. The continuous run lifetime is now largely limited by erosion of the spark-gap-based pulsed power that drives the electron beams. An all solid-state system has been developed to replace this spark-gap system. It is based on components that have demonstrated lifetimes in excess of 300,000,000 pulses. A 180 kV, 5 kA subscale demonstrator (
$1/ 20$ size needed for Electra) based on these technologies has run continuously at 10 Hz for over 11,500,000 pulses (
${\gt }13$ days)[Reference Hegeler, McGeoch, Sethian, Sanders, Glidden and Myers29]. A KrF physics code, called Orestes, has been developed that accurately predicts the performance of several different KrF lasers, operating under significantly different conditions, and at several different laboratories worldwide. The code includes electron deposition and transport, KrF kinetics following 22 species and 130 reactions, and laser transport[Reference Giuliani, Petrov and Dasgupta30], and is useful for designing any size KrF system.
To summarize the status: using a scalable demonstration, a KrF laser has been shown to meet the fusion energy requirements for repetition rate, beam smoothing, wavelength, and bandwidth. Based on the experimental results, an IFE size system is expected to meet the efficiency requirements. It is expected that incorporation of an all solid-state pulsed power system would make significant advances towards meeting the durability requirements.
Acknowledgements
Stephen E. Bodner was partially supported by Berkeley Research Associates. Andrew J. Schmitt and John D. Sethian were supported by the US DoE/NNSA. The authors gratefully acknowledge many suggestions by Stephen Obenschain that were incorporated into this review article.
Open access
