1. Introduction
Nuclear fusion ignition by inertial confinement induced by lasers[Reference Nuckolls, Wood, Hiessen and Immerman1] is very promising and is at the forefront of research today[Reference Velarde and Carpintero-Santamaria2,Reference Mima, Murakami, Nakai, Eliezer and Mima3] . It is expected to be achieved with the megajoule laser of a few nanoseconds pulse duration at the Livermore National Laboratory in the USA [Reference Moses4].
In order to ignite a deuterium–tritium (DT) target with less energy, it was suggested[Reference Basov, Guskov and Feoktistov5,Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason6] to separate the drivers that compress and ignite the target. This idea is called fast ignition. First, the pellet is compressed by a laser system with a few nanoseconds pulse duration; then a second driver, for example a multi-petawatt laser beam, ignites a small part of the pellet. The alpha particles produced in the DT reactions heat the rest of the target.
The main problem of fast ignition is that the laser pulse does not penetrate directly into the compressed target since the electron density of the compressed target is too high, by a few orders of magnitude. In order to overcome this problem, fast ignition by laser-induced shock waves[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov7] or impact-induced shock waves[Reference Murakami, Nagatomo, Azechi, Ogando, Perlado and Eliezer8–Reference Eliezer and Martinez Val10] were suggested in the literature. In the impact case the foil was accelerated by a laser system.
Ultrahigh accelerations of the order of 1020 cm/s2 were predicted for high density plasma blocks created in sub-picosecond laser pulses with more than terawatt intensity. This effect was obtained by using two fluid simulations for laser–plasma interaction where the nonlinear ponderomotive force was dominant[Reference Hora11,Reference Lalousis, Földes and Hora12] . Ion acceleration by ponderomotive force to relativistic velocities was also obtained using particles in cell simulations[Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima13,Reference Robinson, Zepf, Kar, Evans and Bellei14] . This acceleration is similar to the old proposal to accelerate space ships to relativistic velocities by laser pressure radiation[Reference Marx15,Reference Simmons and McInnes16] . Ion acceleration in thin films driven by laser pressure in the domain of 1018 W/cm2 was reported[Reference Maksimchuk, Gu, Flippo, Umstadter and Bychenkov17].
In a recent paper[Reference Eliezer18], the possibility of fast ignition induced by a heat wave was suggested. In this paper we clarify the necessary conditions for the heat wave ignition of an inertial fusion energy system. For impact fast ignition we prove that the micro-foil should have very high velocity. These high velocities can be achieved by laser acceleration. As is well known[Reference Eliezer19], for laser irradiances much larger than 
$1{0}^{16} ~\mathrm{W} / {\mathrm{cm} }^{2} $ the ponderomotive force is the dominant force, and it can accelerate a foil. The acceleration of the micro-foil by a picosecond multi-petawatt laser is calculated analytically in this paper.
In Section 2 two the relativistic acceleration of the foil is given, while in Section 3 the criterion for fast ignition by a heat wave is developed for a ring with cylindrical geometry. Section 4 is a discussion of our results.
2. Relativistic acceleration of a micro-foil
For very high laser irradiance, a foil is accelerated by the electromagnetic (EM) radiation pressure, as described schematically in Figure 1. The radiation pressure is a Lorentz invariant, therefore satisfying 
$P= {P}_{F} $. The physical quantities in the instantaneous rest frame of reference of the micro-foil are denoted by a subscript 
$F$ and their laboratory frame of reference values are denoted without any subscript or with a subscript 
$f$ for the foil variables.
Figure 1. Laser acceleration of a micro-foil in the laboratory and the rest frame of references.
${R}_{F} $ and 
${T}_{F} $ are the reflection and transmission, defined as the ratio between the reflected (transmitted) laser intensity and the incoming laser intensity in the in the 
$F$-frame of reference, satisfying 
${R}_{F} + {T}_{F} = 1$. The laboratory laser irradiance 
$I$ is related to the laser irradiance in the micro-foil rest frame 
${I}_{F} $ through the Lorentz transformation relations. 
${u}_{f} $ is the micro-foil velocity in the laboratory and the dimensionless foil velocity is defined by 
${\beta }_{f} = {u}_{f} / c$, where 
$c$ is the speed of light. The laser irradiance 
$I$ and the pressure 
$P$ are given by
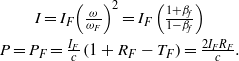$$\begin{aligned}\displaystyle I=& {I}_{F} {\left(\frac{\omega }{{\omega }_{F} } \right)}^{2} = {I}_{F} \left(\frac{1+ {\beta }_{f} }{1- {\beta }_{f} } \right) \\ \displaystyle P= {P}_{F}& = \frac{{I}_{F} }{c} \left(1+ {R}_{F} - {T}_{F} \right)= \frac{2{I}_{F} {R}_{F} }{c} . \displaystyle \end{aligned}$$ For 
${R}_{F} = 1$, Equation (1) implies a pressure
$$P= \frac{2I}{c} \left(\frac{1- {\beta }_{f} }{1+ {\beta }_{f} } \right).$$ We assume that all particles of the micro-foil have the same mass 
$m$, momentum 
${p}_{1} = {m}_{\gamma f} {u}_{f} $ and energy 
${E}_{1} = {m}_{\gamma f} {c}^{2} = \mathop{({m}^{2} {c}^{4} + { p}_{1}^{2} {c}^{2} )}\nolimits ^{1/ 2} $, where 
${\gamma }_{f} = \mathop{(1- { \beta }_{f}^{2} )}\nolimits ^{- 1/ 2} $. The mass of the micro-foil is 
${M}_{0f} = {\rho }_{0} Sl$ and its momentum 
${p}_{f} = {M}_{0f\gamma f} {\beta }_{f} c$, where 
${\rho }_{0} $ is the initial density, 
$S$ the cross section area and 
$l$ the thickness of the micro-foil.
Newton’s law of motion in the laboratory frame of reference is
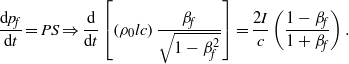$$\frac{\mathrm{d} {p}_{f} }{\mathrm{d} t} = PS\Rightarrow \frac{\mathrm{d} }{\mathrm{d} t} \left[\left({\rho }_{0} lc\right)\frac{{\beta }_{f} }{ \sqrt{1- { \beta }_{f}^{2} } } \right]= \frac{2I}{c} \left(\frac{1- {\beta }_{f} }{1+ {\beta }_{f} } \right).$$ This equation can be easily integrated for a constant 
$I$:
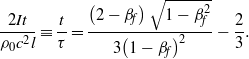$$\frac{2It}{{\rho }_{0} {c}^{2} l} \equiv \frac{t}{\tau } = \frac{\left(2- {\beta }_{f} \right) \sqrt{1- { \beta }_{f}^{2} } }{3{\left(1- {\beta }_{f} \right)}^{2} } - \frac{2}{3} .$$ The solution of Equation (4) is described in Figure 2. In this figure, the micro-foil velocity 
${\beta }_{f} $ is given as a function of the laser pulse duration 
$t$ in units of 
$\tau = {\rho }_{0} {c}^{2} l/ (2I)$, where 
${\rho }_{0} $ is the initial density, 
$l$ is the foil thickness and 
$I$ is the laser intensity. From this solution, one can see that 
${\beta }_{f} \rightarrow 1$ for 
$t/ \tau \rightarrow \infty $, namely, relativistic velocities are obtained if the laser pulse duration 
$t$ is much larger than 
$\tau $. For example, if 
${\rho }_{0} l= 1{0}^{- 5} ~\mathrm{g} / {\mathrm{cm} }^{2} $ and 
$I= 1{0}^{22} ~\mathrm{W} / {\mathrm{cm} }^{2} $, then the dimensionless time 
$t$ is about 50 fs.
Figure 2. Micro-foil velocity as a function of the laser pulse duration 
$t$ in units of 
$\tau = {\rho }_{0} {c}^{2} l/ (2I)$, where 
${\rho }_{0} $ is the initial density, 
$l$ is the foil thickness and 
$I$ is the laser intensity.
The relativistic kinetic energy of the micro-foil 
${W}_{Kf} $ is given by
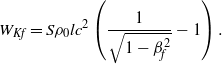$${W}_{Kf} = S{\rho }_{0} l{c}^{2} \left(\frac{1}{ \sqrt{1- { \beta }_{f}^{2} } } - 1\right).$$ It is also useful to know the kinetic energy per atom 
${\varepsilon }_{Kf} $ and the kinetic energy per nucleon 
${\varepsilon }_{1} $:
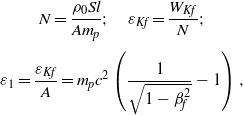$$\begin{array}{ @{}c@{}} \displaystyle N= \displaystyle \frac{{\rho }_{0} Sl}{A{m}_{p} } ; \quad {\varepsilon }_{Kf} = \frac{{W}_{Kf} }{N} ; \\ \displaystyle {\varepsilon }_{1} = \frac{{\varepsilon }_{Kf} }{A} = {m}_{p} {c}^{2} \displaystyle \left(\frac{1}{ \sqrt{1- { \beta }_{f}^{2} } } - 1\right), \end{array} $$ where 
$N$ is the number of atoms in the micro-foil, 
$A$ is the atomic number and 
${m}_{p} $ is the proton mass.
For example, consider an aluminum foil (
$A= 27$, 
${\rho }_{0} = 2. 7~\mathrm{g} / {\mathrm{cm} }^{3} $; 
${m}_{Al} {c}^{2} \approx 27{m}_{p} {c}^{2} \approx 27~\mathrm{GeV} $) with dimensions 
$l= 0. 1~\mathrm{\mu} \mathrm{m} $, 
$S= 10~\mathrm{\mu} {\mathrm{m} }^{2} $, implying 
$N$ (Al atoms) 
$= 6\times 1{0}^{10} $. For 
$\beta = 0. 99$, 
$\beta = 0. 9$ and 
$\beta = 0. 5$, one has accordingly 
${W}_{Kf} \approx 1500$ J, 
${\varepsilon }_{Kf} \approx 150~\mathrm{GeV} $, 
${e}_{1} \approx 5. 5~\mathrm{GeV} $, 
${W}_{Kf} \approx 300~\mathrm{J} $, 
${\varepsilon }_{Kf} \approx 30~\mathrm{GeV} $, 
${e}_{1} \approx 1. 1~\mathrm{GeV} $ and 
${W}_{Kf} \approx 40~\mathrm{J} $, 
${\varepsilon }_{Kf} \approx 4~\mathrm{GeV} $, 
${e}_{1} \approx 0. 15~\mathrm{GeV} $.
Using Equation (4), the laser energy 
${W}_{L} = ISt$ is
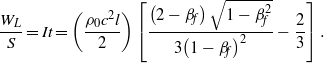$$\frac{{W}_{L} }{S} = It= \left(\frac{{\rho }_{0} {c}^{2} l}{2} \right)\left[\frac{\left(2- {\beta }_{f} \right) \sqrt{1- { \beta }_{f}^{2} } }{3{\left(1- {\beta }_{f} \right)}^{2} } - \frac{2}{3} \right].$$ Equation (7) is described in Figure 3 for 
${\rho }_{0} l$: 
$1{0}^{- 4} $, 
$2. 7\times 1{0}^{- 5} $ and 
$1{0}^{- 5} ~\mathrm{g} / {\mathrm{cm} }^{2} $.
Figure 3. Laser energy per unit area as a function of micro-foil velocity (in units of c).
The energy efficiency of the acceleration is given by
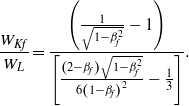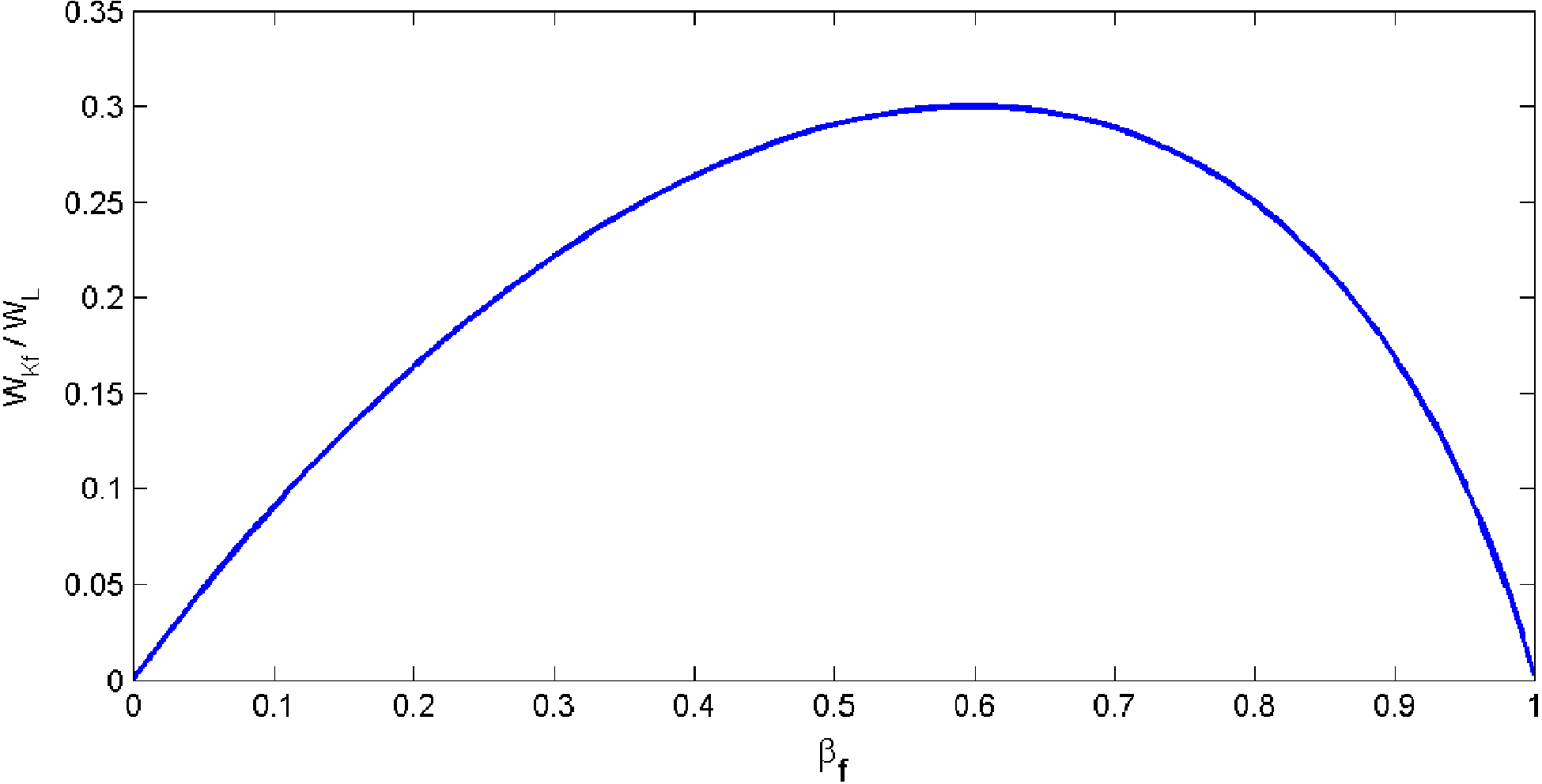
$$\frac{{W}_{Kf} }{{W}_{L} } = \frac{\left(\frac{1}{ \sqrt{1- { \beta }_{f}^{2} } } - 1\right)}{\left[\frac{\left(2- {\beta }_{f} \right) \sqrt{1- { \beta }_{f}^{2} } }{6{\left(1- {\beta }_{f} \right)}^{2} } - \frac{1}{3} \right]} .$$ As one can see from Figure 4, the maximum efficiency is 0.3 for 
${\beta }_{f} = 0. 6$.
Figure 4. Acceleration efficiency (
${= }{W}_{Kf} / {W}_{L} $) of the micro-foil acceleration as a function of micro-foil velocity (in units of c).
3. Criterion for fast ignition by heat wave
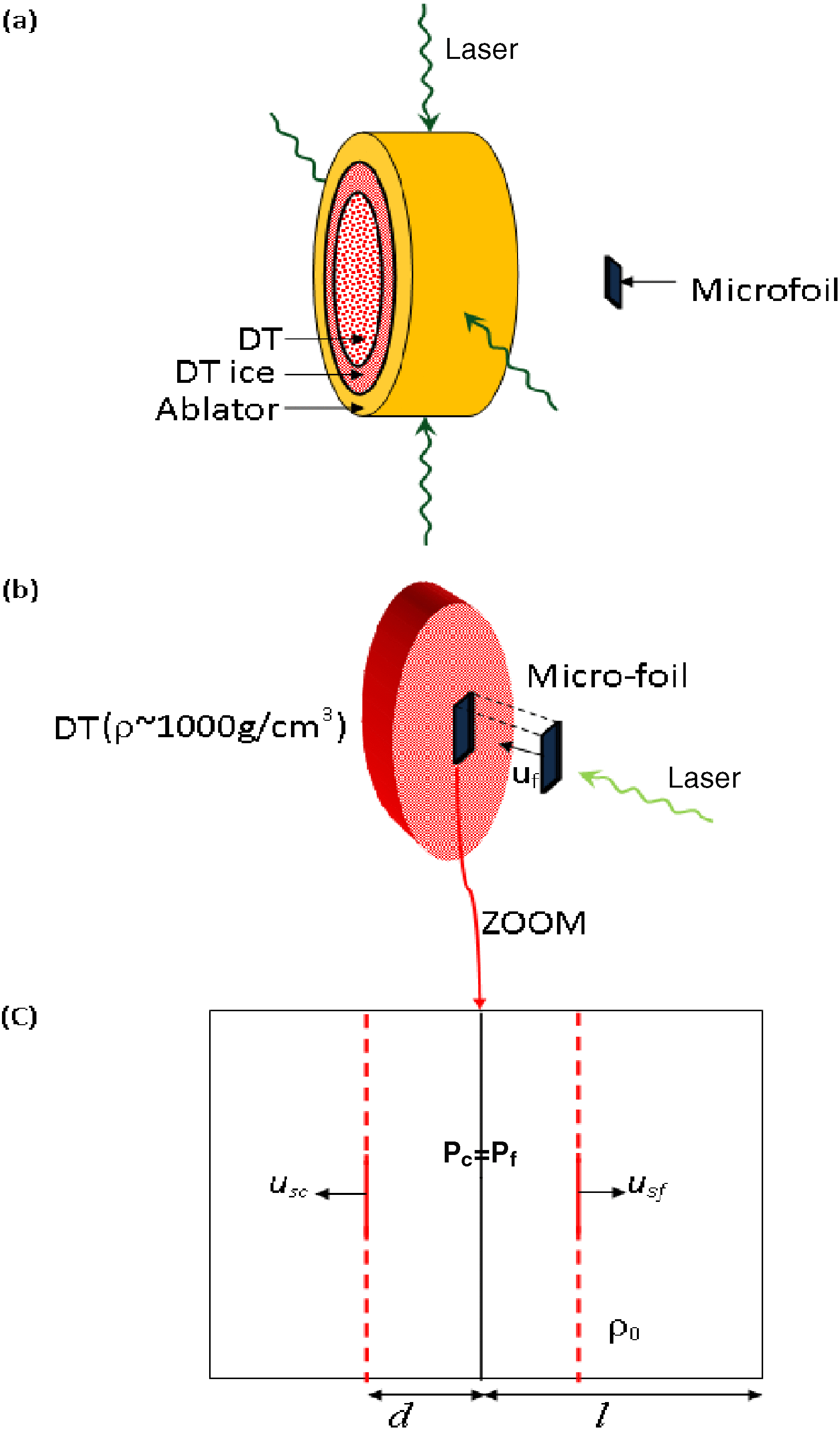
In this section, we calculate the criterion for a heat wave ignition in an inertial fusion energy system. Figure 5(a) describes schematically the compression of a ring with cylindrical geometry, and Figure 5(b) its fast ignition by an accelerated foil. Upon impact, two shock waves are created in the compressed target and in the micro-foil, as described in Figure 5(c). Under appropriate conditions that are further discussed in this section, a heat wave will move into the compressed target before the shock wave front, and it will cause the desired ignition of the compressed fuel.
Figure 5. (a) Nanosecond laser pulses compressing a ring target. (b) A multi-petawatt picosecond laser pulse accelerating a micro-foil into the pre-compressed target. (c) The impact shock waves upon the collision of the micro-foil with the pre-compressed target.
The standard ignition in the literature is caused by an induced shock wave[Reference Betti, Zhou, Anderson, Perkins, Theobald and Solodov7,Reference Eliezer and Martinez Val10] . For a high pressure shock wave with the notation of Figure 5(c), one gets
$$\begin{array}{ @{}c@{}} \displaystyle {P}_{C} = {P}_{f} \Rightarrow {\rho }_{0} { u}_{fs}^{2} \approx {\rho }_{C} { u}_{Cs}^{2} \\ \displaystyle d= {u}_{Cs} t= {u}_{Cs} \left(l/ {u}_{fs} \right)\approx \mathop{({\rho }_{0} / {\rho }_{C} )}\nolimits ^{1/ 2} l. \end{array}$$ Using Equation (9), the ‘
$\rho {R}_{\alpha } $’ value of the hot spot where the alpha absorption length equals the shock wave thickness in the compressed target is
$${\rho }_{C} d\approx l\mathop{({\rho }_{0} {\rho }_{C} )}\nolimits ^{1/ 2} .$$ The ignition criterion is based on the requirement that the alpha particles created in the DT reaction are reabsorbed in the hot spot, implying a ‘
$\rho {R}_{\alpha } $’ value larger than 
$0. 3~\mathrm{g} / {\mathrm{cm} }^{2} $ for a temperature (in energy units) about 10 keV (and larger values for higher temperatures). Therefore Equation (10) requires
$$l\mathop{({\rho }_{0} {\rho }_{C} )}\nolimits ^{1/ 2} \geq 0. 3~\mathrm{g} / {\mathrm{cm} }^{2} .$$ In the shock wave ignition for the case described before (
$l= 0. 1~\mathrm{\mu} \mathrm{m} $, 
${\rho }_{0} = 1~\mathrm{g} / {\mathrm{cm} }^{3} $ and 
${\rho }_{C} = 1000~\mathrm{g} / {\mathrm{cm} }^{3} $), ‘
$\rho {R}_{\alpha } $’ 
$= l\mathop{({\rho }_{0} {\rho }_{C} )}\nolimits ^{1/ 2} \sim 0. 003~\mathrm{g} / {\mathrm{cm} }^{2} $, which is two orders of magnitude too low. From this ignition criterion in the hot spot we need to increase the foil thickness by two orders of magnitude, which implies the undesired result of increasing the accelerating driver energy by two orders of magnitude.
Our scheme is based on heat wave ignition. The local absorption of the flyer energy is associated with the creation of a temperature gradient and a thermal flux in order to transport the absorbed energy. If the interaction of the impact is very short, of the order of 1 ps or less, the hydrodynamic motion does not have time to develop, and therefore the heat transport is dominant. Electrons or x-rays may serve as heat carriers. For a nonlinear transport coefficient, like the electron conductivity, we expect that the energy transport is caused by a heat wave. This heat wave plays an important role in the inertial confinement fusion during the ignition process.
The nonlinear heat transport equation and the energy conservation are described accordingly by[Reference Eliezer19,Reference Zeldovich, Raizer, Hayes and Probstein20]
$$\frac{\partial T}{\partial t} = a\frac{\partial }{\partial x} \left({T}^{n} \frac{\partial T}{\partial x} \right); \quad \int \nolimits T(x, t)\mathrm{d} x= \frac{{W}_{hw} }{S{\rho }_{C} {C}_{V} } ,$$ where 
$T(x, t)$ is the temperature in degrees Kelvin at position 
$x$ and time 
$t$. The thermal diffusivity 
$a{T}^{n} ~({\mathrm{cm} }^{2} / \mathrm{s} )$ in our case is taken for 
$n= 5/ 2$ with 
$a$ being a constant. 
${\rho }_{C} $ is the density of the compressed target, and it is assumed constant during the heat wave transition. 
${C}_{V} $ is the specific heat at constant volume 
$[\mathrm{erg} / (\mathrm{g} \cdot \mathrm{K} )] $ and 
${W}_{hw} / S$ is the heat wave energy per unit area. The solution of Equation (12) is
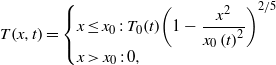$$T(x, t)= \left\{ \begin{array}{ @{}l@{}} \displaystyle x\leq {x}_{0} : {T}_{0} (t){\left(1- \frac{{x}^{2} }{{x}_{0} \mathop{(t)}\nolimits ^{2} } \right)}^{2/ 5} \\ \displaystyle x\gt {x}_{0} : 0, \end{array} \right.$$ where 
${T}_{0} $ and 
${x}_{0} $ are the temperature at 
$x= 0$ and the front coordinate of the heat wave, respectively. Figure 6 describes the solution of Equation (13) for a heat wave space profile at three times, 
${t}_{1} \gt {t}_{2} \gt {t}_{3} $.
Figure 6. Heat wave temperature space profile at three times, 
${t}_{1} \gt {t}_{2} \gt {t}_{3} $.
The second equation of (12) with 
${C}_{V} = 3{k}_{B} / (2. 5{m}_{p} )$ for a DT ideal gas yields approximately
$${W}_{hw} \approx {T}_{0} {x}_{0} S{\rho }_{C} \left(\frac{3{k}_{B} }{2. 5{m}_{p} } \right).$$ Defining the efficiency 
${\eta }_{h} w$ as the ratio of the heat wave energy 
${W}_{hw} $ in the compressed target to the foil kinetic energy 
${W}_{Kf} $, then one can write the energy relation:
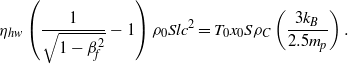$${\eta }_{hw} \left(\frac{1}{ \sqrt{1- { \beta }_{f}^{2} } } - 1\right){\rho }_{0} Sl{c}^{2} = {T}_{0} {x}_{0} S{\rho }_{C} \left(\frac{3{k}_{B} }{2. 5{m}_{p} } \right). \quad$$ In order to ignite the DT fuel, the alpha particles created in the DT reaction are reabsorbed in the hot spot, implying a ‘
$\rho {R}_{\alpha } $’ value larger than 
$0. 3~\mathrm{g} / {\mathrm{cm} }^{2} $ for a temperature about 10 keV; therefore
$${x}_{0} {\rho }_{C} \geq 0. 3~(\mathrm{g} / {\mathrm{cm} }^{2} ).$$Equations (15) and (16) imply the criterion for high gain nuclear fusion ignition of DT fuel:
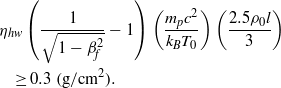$$\displaystyle {\eta }_{hw} \left(\frac{1}{ \sqrt{1- { \beta }_{f}^{2} } } - 1\right)\left(\frac{{m}_{p} {c}^{2} }{{k}_{B} {T}_{0} } \right)\left(\frac{2. 5{\rho }_{0} l}{3} \right)\quad \geq 0. 3~(\mathrm{g} / {\mathrm{cm} }^{2} ).$$The criterion of Equation (17) can be described as a requirement on the micro-foil velocity by the following:
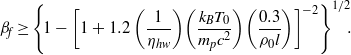$${\beta }_{f} \geq {\left\{\hspace {-2pt}1- {\left[1+ 1. 2\left(\frac{1}{{\eta }_{hw} } \right)\hspace {-2pt}\left(\frac{{k}_{B} {T}_{0} }{{m}_{p} {c}^{2} } \right)\hspace {-2pt}\left(\frac{0. 3}{{\rho }_{0} l} \right)\right]}^{- 2} \right\}}^{1/ 2} \hspace {-3pt}. \quad$$ For example, Equation (16) and a pre-compressed target of 
$1000~\mathrm{g} / {\mathrm{cm} }^{3} $ require a heat wave front larger than 3 microns. Furthermore, 
${k}_{B} {T}_{0} = 10$ keV, 
${\rho }_{0} (Al)= 2. 7~\mathrm{g} / {\mathrm{cm} }^{3} $, 
$l= 0. 1~\mathrm{\mu} \mathrm{m} $ and assuming 
${\eta }_{hw} = 1$ requires a foil velocity of 
${\beta }_{f} \geq 2/ 3$, implying a laser energy 
${W}_{L} \geq 135~\mathrm{J} $ (see Equation (7)).
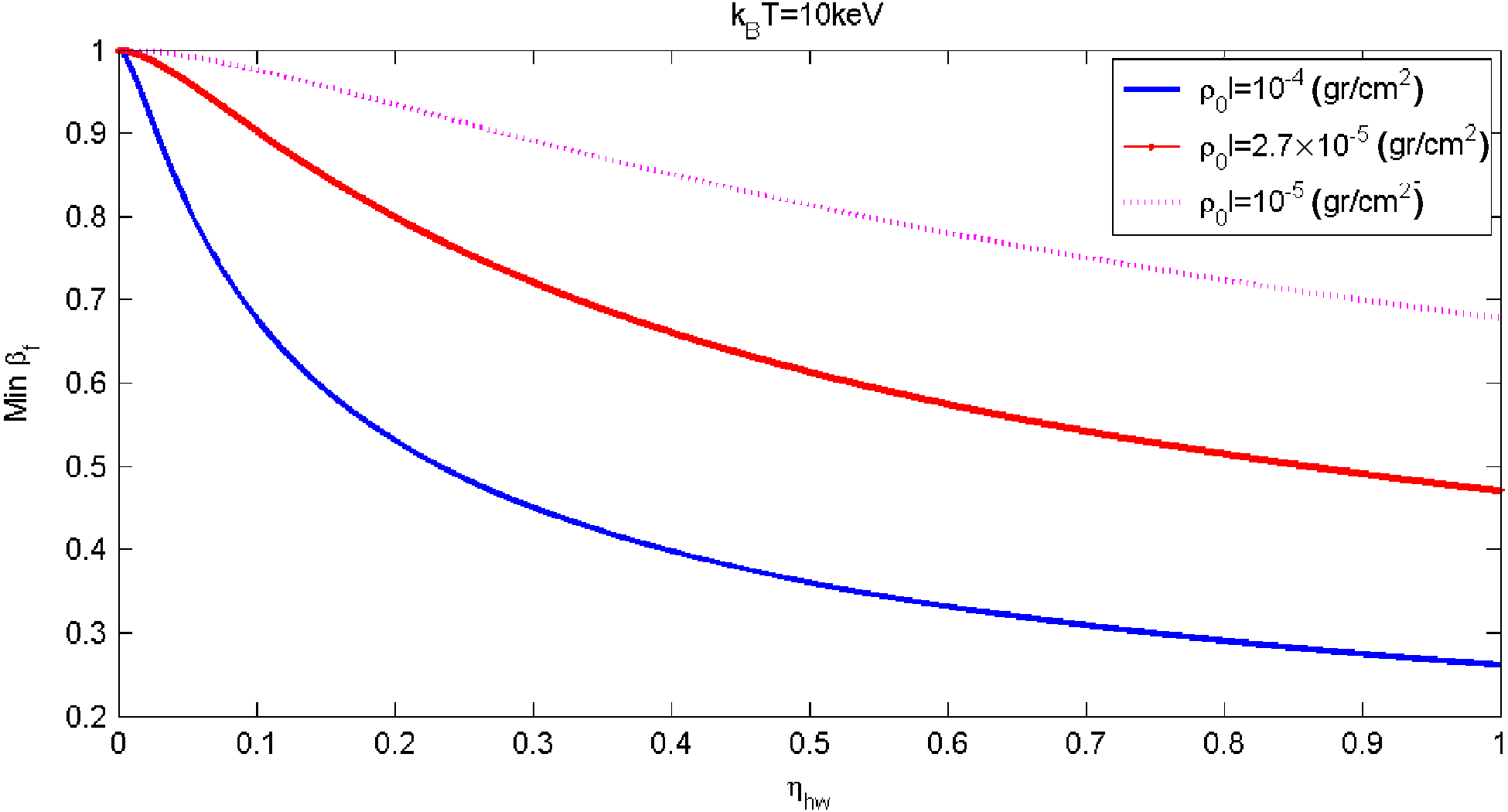
This section is concluded with Figure 7, where the micro-foil velocity threshold for heat wave fast ignition of deuterium–tritium (DT) fuel is given for three cases of 
${\rho }_{0} l$: 
$1{0}^{- 4} $, 
$2. 7\times 1{0}^{- 5} $ and 
$1{0}^{- 5} ~\mathrm{g} / {\mathrm{cm} }^{2} $.
Figure 7. The micro-foil velocity threshold for heat wave fast ignition of deuterium–tritium (DT) fuel as a function of the heat efficiency for three cases of 
${\rho }_{0} l$: 
$1{0}^{- 4} $, 
$2. 7\times 1{0}^{- 5} $ and 
$1{0}^{- 5} ~\mathrm{g} / {\mathrm{cm} }^{2} $.
4. Discussion
In this paper, it is suggested that the ponderomotive force, induced by a multi-petawatt laser on the interface of a vacuum with solid target, can accelerate a micro-foil to relativistic velocities. Extremely high velocities of the micro-foil are achieved in a very short time duration (
$\sim \hspace {-2pt}$ picosecond) of the laser pulse.
The accelerated micro-foil is used to ignite a pre-compressed cylindrical shell containing deuterium–tritium fuel. The shock wave ignition criterion is given by the known relation of Equation (11). Our proposal is based on heat wave ignition, and the novel criterion developed in this work is given by Equation (18).
An important point of consideration is the ‘inhibition factor’ that might reduce the thermal conduction. The inhibition factor was originally introduced in laser–plasma interaction to describe the electron transport from the absorption area to the ablation domain in the plasma region[Reference Eliezer19]. A more comprehensive discussion of this factor is given in the literature,[Reference Hora11,Reference Lalousis, Földes and Hora12] . In our impact case the heat wave is generated as suggested by[Reference Zeldovich, Raizer, Hayes and Probstein20] and analyzed in this paper. Further experiments and simulations are needed in order to understand this problem.
Due to the significantly higher temperature that can be achieved upon impact of a relativistic micro-foil with a pre-compressed target, this scheme may be appropriate also for clean proton–boron11 fusion. The analysis and the heat wave requirements for the cleanest fusion reaction will be discussed in a separate paper.
The gain 
$G$ can be analytically estimated[Reference Eliezer, Murakami and Martinez Val21]. For the cylindrical shell in Figure 5 we use the notation 
${M}_{0} = \mathrm{initial} $ mass, 
${\rho }_{0} = \mathrm{density} $, 
${R}_{0} = \mathrm{ring} $ radius, 
$\Delta {R}_{0} = \mathrm{thickness} $, 
$L= \mathrm{ring} $ length, 
${R}_{C} = \mathrm{final} $ radius of compression, the aspect ratio 
${A}_{r} = {R}_{0} / \Delta {R}_{0} $, 
$\phi = \mathrm{burning} $ fraction of DT, 
${\eta }_{C} = \mathrm{laser} $ to compression efficiency and 
${W}_{d} = \mathrm{driver} $ energy. The following set of equations calculates the gain for our cylindrical geometry:
$$\displaystyle \frac{{\rho }_{C} }{{\rho }_{0} } = \displaystyle \left(\frac{2}{{A}_{r} } \right){\left(\frac{{R}_{0} }{{R}_{C} } \right)}^{2}$$
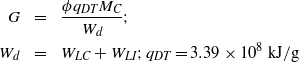$$\displaystyle G= \displaystyle \frac{\phi {q}_{DT} {M}_{C} }{{W}_{d} } ; {W}_{d} = {W}_{LC} + {W}_{LI} ; {q}_{DT} = 3. 39\times 1{0}^{8} ~\mathrm{kJ} / \mathrm{g}$$
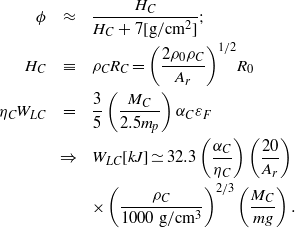$$\begin{eqnarray}\displaystyle \phi &\approx &\displaystyle \frac{{H}_{C} }{{H}_{C} + 7[\mathrm{g} / {\mathrm{cm} }^{2} ] } ; \\\displaystyle {H}_{C} &\equiv &\displaystyle {\rho }_{C} {R}_{C} = {\left(\frac{2{\rho }_{0} {\rho }_{C} }{{A}_{r} } \right)}^{1/ 2} {R}_{0} \\\displaystyle {\eta }_{C} {W}_{LC} &= &\displaystyle \frac{3}{5} \left(\frac{{M}_{C} }{2. 5{m}_{p} } \right){\alpha }_{C} {\varepsilon }_{F} \\\displaystyle &\Rightarrow &\displaystyle {W}_{LC} [kJ] \simeq 32. 3\left(\frac{{\alpha }_{C} }{{\eta }_{C} } \right)\left(\frac{20}{{A}_{r} } \right)\\\displaystyle &&\displaystyle \times \,{\left(\frac{{\rho }_{C} }{1000~\mathrm{g} / {\mathrm{cm} }^{3} } \right)}^{2/ 3} \left(\frac{{M}_{C} }{mg} \right).\end{eqnarray}$$ Since the laser energy that compresses the target 
${W}_{LC} $ is much larger than the laser energy that accelerates the foil 
${W}_{Lf} $, one has 
${W}_{d} \approx {W}_{LC} $. 
${\alpha }_{C} $ is an equation of state parameter showing the approach to an isentropic compression. The following example gives an indication ofthe parameters and gain of Equations (20) and (21): 
${\rho }_{C} = 1000~\mathrm{g} / {\mathrm{cm} }^{3} $, 
${\rho }_{0} = 0. 2~\mathrm{g} / {\mathrm{cm} }^{3} $, 
${A}_{r} = 20$, 
$L= 0. 05{R}_{0} $, implying 
$\phi = 0. 3$, 
${\rho }_{C} {R}_{C} = 3~\mathrm{g} / {\mathrm{cm} }^{2} $, 
${M}_{C} = 0. 85~\mathrm{mg} $ and 
${W}_{LC} = 0. 8~\mathrm{MJ} $. For 
${\eta }_{C} $ of only 10% and an equation of state parameter 
${\alpha }_{C} = 3$[Reference Rosen22] we get a gain of 
$G= 100$.
A similar analytic calculation for the spherical geometry impact fast ignition case has been given[Reference Eliezer and Martinez Val10,Reference Eliezer, Murakami and Martinez Val21] . In this case, a laser driver with an order of magnitude less energy was suggested. It is interesting to point out that hydrodynamic simulations [Reference Azechi, Sakaiya, Watari, Karasik, Saito, Ohtani, Takeda, Hosoda, Shiraga, Nakai, Shigemori, Fujioka, Murakami, Nagatomo, Johzaki, Gardner, Colombant, Bates, Velikovich, Aglitskiy, Weaver, Obenschain, Eliezer, Kodama, Norimatsu, Fujita and Mima9] gave a good agreement with the analytical calculations. Therefore, to a good approximation it is conceivable that the energy suggested in this paper is a reasonable result; however, a proper hydrodynamic simulation is required in order to confirm our results. Furthermore, two-dimensional axi-symmetric cylindrical geometry simulations are very important in the design of more sophisticated targets.
The cylindrical geometry suggested here for the fast ignition approach has the advantage of geometrically separating the nanosecond lasers that compress the target and the picosecond laser that accelerates the foil. The present model suggests that nuclear fusion by micro-foil impact ignition could be attained with currently existing technology [Reference Moses4].
Open access
