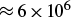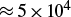1 Introduction
The generation of laser-driven particle sources is a current hot topic in physics research with implications that go from laser-driven fusion (and in particular the proton-driven fast ignition approach to inertial fusion[ Reference Macchi, Antonicci, Atzeni, Batani, Califano, Cornolti, Honrubia, Lisseikina, Pegoraro and Temporal 1 ]) to the realization of several societal or industrial applications[ Reference Daido, Nishiuchi and Pirozhkov 2 ].
Also, in recent years, high yields of α-particles have been observed from laser-driven hydrogen–boron fusion experiments, opening the possibility to develop a novel approach to high-brightness α-particle sources[ Reference Belyaev, Matafonov, Vinogradov, Krainov, Lisitsa, Roussetski, Ignatyev and Andrianov 3 – Reference Belyaev, Krainov, Matafonov and Zagreev 6 ]. These experiments are based on the hydrogen–boron fusion reaction[ Reference Oliphant and Rutherford 7 , Reference Zhang, Xu, Xu, Wei, Ren, Chen, Ma, Hu, Li, Liu, Yang, Lai, Yue, Xiong, Xu, Chen, Wang, Zhou, Shi, Cheng, Deng, Qi, Zhou, Zhao, Liu, Luo, Hofmann and Zhao 8 ]:
$$\begin{align}p +^{11}\mathrm{B}\to 3\left({\;}^4\mathrm{He}\right)+8.7\;\mathrm{MeV},\end{align}$$
and have used two different mainstream schemes: the pitcher–catcher configuration (Figure 1) and in-target irradiation. In the in-target irradiation scheme, the laser beam directly interacts with the boron target (containing hydrogen impurities)[ Reference Picciotto, Margarone, Velyhan, Bellutti, Krasa, Szydlowsky, Bertuccio, Shi, Mangione, Prokupek, Malinowska, Krousky, Ullschmied, Laska, Kucharik and Korn 9 – Reference Margarone, Bonvalet, Giuffrida, Morace, Kantarelou, Tosca, Raffestin, Nicolaï, Picciotto, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Batani 12 ]. Here, both boron and hydrogen nuclei are accelerated by various mechanisms (including laser hole boring) to finally react, releasing the three α-particles.
Figure 1 Scheme of the experimental setup. In the configuration with the BNH6 catcher, the pitcher–catcher distance was 2 cm, the catcher–CR39 distance was 52 cm and the angle between laser propagation and catcher normal was 50°. The TNSA shielding prevented protons and other ions emitted from the pitcher reaching the CR39.
In the pitcher–catcher scheme, the laser irradiates a pitcher (usually Al or plastic thin foils), producing a proton beam, which is sent onto the catcher, a secondary boron target where the proton-boron (pB) fusion reactions take place[ Reference Labaune, Baccou, Depierreux, Goyon, Loisel, Yahia and Rafelski 13 – Reference Bonvalet, Nicolaï, Raffestin, D’humieres, Batani, Tikhonchuk, Kantarelou, Giuffrida, Tosca, Korn, Picciotto, Morace, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Margarone 16 ]. Most experiments within this approach used high-energy, high-power laser beams to produce a bright source of protons through the mechanisms of target normal sheath acceleration (TNSA)[17– Reference Passoni, Perego, Sgattoni and Batani 21 ].
One critical issue is, however, how to measure the α-yield in a reliable way. The most common diagnostic used in such experiments relies on solid-state nuclear track detectors (CR39)[ Reference Ingenito, Andreoli, Batani, Bonasera, Boutoux, Burgy, Cipriani, Consoli, Cristofari, De Angelis, Di Giorgio, Ducret, Giulietti and Jakubowska 22 ], for which an α-particle identification might be a problem due to the simultaneous emission of many ion species from the laser-irradiated targets. Many other diagnostics used in these experiments (Thomson parabolas, time-of-flight detectors, …) are also prone to this problem (for a full discussion on the topic see, e.g., Refs. [23–25]).
There is indeed another important issue: CR39 and other diagnostics only measure the α-particles escaping the targets; however, due to their very short propagation range in solid density matter most α-particles are unable to emerge and are indeed trapped inside the boron target.
Therefore, alternative diagnostic approaches are useful to validate experimental results. One of such novel approaches is the detection of radioactive isotopes produced in the targets by secondary nuclear reactions[ Reference Consoli, De Angelis, Andreoli, Bonasera, Cipriani, Cristofari, Di Giorgio, Giulietti and Salvadori 23 , Reference Schollmeier, Shirvanyan, Capper, Steinke, Higginson, Hollinger, Morrison, Nedbailo, Song, Wang, Rocca and Korn 26 , Reference Scisciò, Petringa, Zhe, Rodrigues, Alonzo, Andreoli, Filippi, Consoli, Huault, Raffestin, Molloy, Larreur, Singappuli, Carriere, Verona, Nicolai, McNamee, Ehret, Filippov, Lera, Pérez-Hernández, Agarwal, Krupka, Singh, Lattuada, La Cognata, Guardo, Palmerini, Rapisarda, Batani, Cipriani, Cristofari, Di Ferdinando, Di Giorgio, De Angelis, Giulietti, Jun, Volpe, Giuffrida, Margarone, Batani, Cirrone, Bonasera and Consoli 27 ]. Most of the produced radioisotopes are characterized by γ-ray emission, and therefore the type and number of produced radioisotopes can be characterized by γ-ray spectroscopy, for instance using a calibrated high-purity germanium (HPGe) detector. The number of proton–boron fusion reactions that took place in the target can then be retrieved by the known branching ratio between the pB reaction and the reaction that produced the radioisotopes. Of course, γ-rays can measure the total number of reactions that took place inside the target, so there is no ‘escaping issue’ as for α-particle detection with CR39.
Apart from the diagnostic use, the generation of radioisotopes in laser-driven experiments can be very interesting in itself, in particular for producing radioisotopes for medical applications in therapy or diagnostics, particularly PET (proton emission tomography). Radioisotopes used in medicine are currently produced by neutron irradiation in dedicated research reactors, or by proton irradiation using cyclotrons. In principle, laser-driven sources are able to produce energetic protons and neutrons, and they could be used as a complementary technology to generate radioisotopes for diagnostics and medical treatment[ Reference Rodrigues, Bonasera, Scisciò, Pérez-Hernández, Ehret, Filippi, Andreoli, Huault, Larreur, Singappuli, Molloy, Raffestin, Alonzo, Rapisarda, Lattuada, Guardo, Verona, Consoli, Petringa, McNamee, La Cognata, Palmerini, Carriere, Cipriani, Di Giorgio, Cristofari, De Angelis, Cirrone, Margarone, Giuffrida, Batani, Nicolai, Batani, Lera, Volpe, Giulietti, Agarwal, Krupka, Singh and Consoli 28 , Reference Maffini, Mirani, Giovannelli, Formenti and Passoni 29 ]. In addition, it is also possible to consider radioisotope production using α-particles produced by laser-driven proton–boron fusion. Today, radioisotopes from α-particles sources are little used in the medical domain because, even if often they have very interesting properties, only a few cyclotrons in the world are able to accelerate α-beams with adequate energy and intensity for their production. Usually, the reactions that produce such radioisotopes show maxima in cross-sections for energies higher than 10 MeV[ Reference Szkliniarz, Sitarz, Walczak, Jastrzębski, Bilewicz, Choiński, Jakubowski, Majkowska, Stolarz, Trzcińska and Zipper 30 ]. Only dedicated cyclotrons such as ARRONAX[ Reference Haddad, Ferrer, Arnaud, Carlier, Michel, Barbet and Chatal 31 ] or U-120M[ 32 ] can produce high-flux of α-particles with energies higher than such energies. The cost and the complexity of such dedicated cyclotrons, as well as the need for extensive radioprotection, strongly limit the spread of such technology and access to related radioisotopes.
This is the case for instance of α-emitters such as 211At. The current supplies for medically useful α-emitters such as 211At are limited by naturally isolated by-products from weapons development and the actual level of production is only sufficient for preclinical studies and limited clinical trials. 211At can also be produced by the irradiation of 209Bi with α-particles,[ Reference Guérard, Gestin and Brechbiel 33 ] which could be realized using laser-driven α-particle sources.
Concerning PET, recently, there has been significant interest in the radionuclides of scandium: 44Sc (T 1/2 = 3.87 h) and 43Sc (T 1/2 =3.89 h) as tracers for PET imaging. 43Sc and 44Sc can be produced by irradiating natural calcium with α-particles from cyclotrons, as already shown by the IChTJ group[ Reference Walczak, Krajewski, Szkliniarz, Sitarz, Abbas, Choiński, Jakubowski, Jastrzębski, Majkowska, Simonelli, Stolarz, Trzcińska, Zipper and Bilewicz 34 , Reference Krajewski, Cydzik, Abbas, Bulgheroni, Simonelli, Holzwarth and Bilewicz 35 ] in the Heavy Ion Laboratory of Warsaw University. Alternatively, 43Sc can be produced by irradiating natural Ca with protons, but in this case 44Sc is also produced.
In any case, it is well known that the demand for radioisotopes is rapidly increasing, for both therapy and diagnostics, so there exists a strong societal need for developing new approaches to increasing radioisotope production to meet increasing demand[ 36 , 37 ]. Therefore, it is very important to study the possibility of producing radioisotopes by laser irradiation and, in particular, using laser-driven sources of α-particles based on the proton–boron fusion reaction.
In conclusion, this paper addresses two different but related points: (1) the use of radioisotopes as a diagnostic of α-particle generation in laser-driven proton–boron fusion experiments; and (2) the feasibility of producing medical radioisotopes using laser-generated protons or α-particles.
2 Experimental setup
The experimental investigation was carried out in March 2023 at the Centro de Láseres Pulsados (CLPU) in Salamanca, Spain, using the short-pulse high-intensity laser VEGA-3.
The laser is operating at wavelength λ = 810 nm with the pulse duration τ = 200–250 fs and energy of about 25 J. The laser incidence angle on the pitcher target was Θ = 12o, providing an on-target focal spot size (full width at half maximum (FWHM)) of 12 μm. The temporal contrast was about 2
$\times$
10−5 at 1 ps before the main pulse and below 10−5 at 5 ps.
Although the laser VEGA-3 can work at repetition rates of up to 1 Hz, we did not use such a high repetition rate in our experiment mainly due to the need for performing an accurate alignment of each pitcher target before the laser shots. We made a shot every 2 min, which compared to many experiments with high-intensity lasers can still be considered as a relatively high repetition frequency.
Notice that we have on purpose opted for a non-optimal temporal compression of the VEGA-3 laser pulse. Indeed, the full compressed duration (
$\sim$
30 fs) is not optimal for proton acceleration and a longer pulse is more efficient. We experimentally found that the proton energy and proton number were optimized for pulse durations of 200–250 fs[
Reference Scisciò, Petringa, Zhe, Rodrigues, Alonzo, Andreoli, Filippi, Consoli, Huault, Raffestin, Molloy, Larreur, Singappuli, Carriere, Verona, Nicolai, McNamee, Ehret, Filippov, Lera, Pérez-Hernández, Agarwal, Krupka, Singh, Lattuada, La Cognata, Guardo, Palmerini, Rapisarda, Batani, Cipriani, Cristofari, Di Ferdinando, Di Giorgio, De Angelis, Giulietti, Jun, Volpe, Giuffrida, Margarone, Batani, Cirrone, Bonasera and Consoli
27
].
The experiment was performed in the pitcher–catcher configuration (see Figure 1). We used a remotely controlled target holder containing tens of pitcher foils producing protons after each shot. Such protons were sent on the same catcher in order to accumulate tens of shots and produce a greater and more easily measurable quantity of radioisotopes. We irradiated several kinds of catcher targets: pure boron (B), boron nitride (BN), ammonia borane (BNH6) and calcium silicate (Ca2SiO4).
Produced radioisotopes were measured using an HPGe γ-ray detector, while other diagnostics were used to characterize the proton and the α-particle generation (including CR39 foil, a Thomson parabola spectrometer, time of flight). The general experimental setup is presented in Figure 1.
The Thomson parabola spectrometer was used to characterize the spectrum of TNSA protons emitted from the pitcher in shots where the catcher was not present. For a detailed experimental setup of the laser and diagnostics see Refs. [27,38], which also describe the results of proton and α-particle generation. The results described in Ref. [38] were acquired during the same experiment. Although the pitcher–catcher scheme was also used, Ref. [38] focuses on the hole-boring scheme (i.e., when the laser directly irradiates the target) and addresses the problem of cross-validation of experimental results and detailed computer simulations.
In this paper, we instead just use the pitcher–catcher configuration, which is more adapted to the production of radioisotopes and in particular we describe the results obtained with ammonia borane and calcium silicate catchers, as an example of the possibilities, and the challenges, offered by the laser-driven approach in the production of medical radioisotopes.
3 Characterization and calibration of the germanium γ-ray detector
In the experiment, we used an HPGe γ-ray detector equipped with a DSA-1000, 16K channel integrated multichannel analyzer and cooled with liquid nitrogen (LN2) at 77 K. The housing of the detector was made of passive iron shield of 15 cm in all directions, screening it from external radiation sources, and the samples had to be positioned inside the same housing.
A fundamental point for the interpretation of the experimental measurement is the characterization and calibration of the spectrometer. We used three different γ-radiation sources: 137Cs (emitting a γ line at 661.657 keV), 60Co (emitting two lines at 1173.228 and 1332.492 keV) and a mixed source of 155Eu (86.540 and 105.30 keV) and 22Na (511.00 and 1274.54 keV).
The first step is the calibration with respect to photon energy, that is, the relation between the analyzer channel (pixel) and the energy of the emitted lines. Figure 2 presents the energy calibration of the HPGe γ-ray detector showing a linear relationship between the photon energy and the channel (pixel).
Figure 2 Energy calibration of the HPGe detector: (left) channel–energy relation; (right) superposition of the spectra obtained with the radioactive sources.
The second point is establishing a relation between the number of counts and the activity of the sources, that is, determining the detection efficiency, that is, the relation between radioisotope activity and recorded counts. In order to do this, we must take into account the following.
-
(1) The decay of source activity since the sources were acquired:
(2)
$$\begin{align}N(t)={N}_0\;\mathit{\exp}\left(-\lambda\;t\right)={N}_0\;\mathit{\exp}\left(-\ln (2)\frac{t}{\tau_{1/2}}\;\right).\end{align}$$
-
(2) The activity related to each specific γ-ray energy, which is obtained by multiplying the source activity by the γ emission probability, is represented as ‘γ line activity’.
The results of these calculations are shown in Table 1.
Table 1 Calculation of the activity corresponding to each γ-ray energy in the spectra emitted by the calibration sources.
We then calculated the peak detection efficiency
$D$
as the ratio between the line activity (in kBq) and the recorded number of counts in the γ-ray line, recorded during a 5-min acquisition:
$$\begin{align}D=\frac{\gamma \text{ line activity}}{\text{Number of counts}\;}.\end{align}$$
The results of the calculations are shown in Figure 3, where the photon energy is in keV and the line activity is measured in kBq. We see that the peak detection efficiency
$D$
depends on γ-ray photon energy and that the relation is practically linear (and passing through the origin, i.e.,
$D$
is proportional to
$h\nu$
).
Figure 3 Activity calibration line showing the peak detection efficiency
$D$
as a function of γ-ray photon energy (considering counts recorded during a 5-min acquisition).
We also performed a sensitivity scan by displacing the radioactive source inside the container with respect to the central position (the source placed exactly on the vertical axis of the detector at a fixed distance of 1 cm). Figures 4 and 5, respectively, show the results of displacing the sources in the vertical direction and in the horizontal direction.
Figure 4 γ-ray detector sensitivity variation while displacing the sources in the vertical direction with respect to the detector.
Figure 5 γ-ray detector sensitivity variation while displacing the sources in the horizontal direction with respect to the detector.
The number of recorded counts approximately scales inversely proportionally with respect to the vertical displacement (i.e.,
$\text{Counts}\approx 1/d$
) and linearly with respect to the horizontal displacement.
This measurement is important because it allows estimating the error in the number of recorded counts, which corresponds to non-perfect positioning of the source or to different source geometry. For instance, a displacement of 1 cm in the lateral direction implies a reduction of 10% in counts, while a displacement of 1 cm in the vertical direction implies a reduction of 50% in counts.
In order to analyze the γ-ray spectra, we performed an accurate measurement of the background (due to cosmic rays or other sources) with the same detector, and we then subtracted such background from our experimental spectra.
A final question related to the calibration of the spectrometer concerns the impact of Compton scattering on the recorded spectra. Not all the emitted γ-photons at one energy
$h\nu$
are found in the corresponding line but many undergo Compton scattering (at an angle
$\theta$
) with the electrons in the detector material, after which they might escape the detector volume and therefore are recorded as photons at
$h{\nu}^{\prime}$
:
$$\begin{align}\frac{1}{h\nu^{\prime }}-\frac{1}{h\nu}=\frac{1}{m{c}^2}\left(1- \mathrm{cos}\theta \right).\end{align}$$
Monte Carlo simulations are needed to give a quantitative evaluation of this effect (depending on the detector size and geometry). However, in our setup, we can get an estimation by using the single-line spectrum emitted by the 137Cs source (for multiple-line spectra the situation is more complex due to the superposition of some lines to the Compton shoulder and the superposition of Compton shoulders from different lines).
Figure 6 shows the spectrum of 137Cs in logarithmic scale. Although on a linear scale the Compton shoulder seems small, due to its large energy range, it indeed contains more photons than the line peak. The ratio between the total number of counts and the counts in the peak is
$\approx$
3.5.
Figure 6 Compton shoulder in the spectrum recorded with the 137Cs source having a single-line source at 662 keV in logarithmic scale.
This factor is anyway naturally included in the calibration, which relates the number of counts recorded in the main γ-ray line to the total activity of the source (i.e., including the decay that will end up in the Compton shoulder).
4 Radioisotope generation using BNH 6
We placed an ammonia borane (BNH6) pellet on the rear side of the Al pitcher (6 μm in thickness) at a distance of 2 cm. The pellet had a diameter of 12 mm and a thickness of 1.2 mm, and it was produced by Chris Spindloe et al. [ 39 ] by compression of commercially available BNH6 powder. A detailed discussion of the targets can be found in Refs. [40,41]. The sample was inclined under 50° to the laser propagation axis. After irradiation the sample was placed in the HPGe detector and acquisitions were done every 5 min (accumulating the signal for 5 min). Figure 7 shows the accumulated γ-ray spectrum recorded after the irradiation over the period of 100 min and measured for 60 min, showing a strong peak at 511 keV.
Figure 7 γ-ray spectrum recorded from a BNH6 (ammonia borane) pellet irradiated with 31 laser shots (accumulation time over 100 min).
Since the 511 keV line is due to the annihilation of positrons emitted from radioisotopes with the electron in the material, it is typical of any β+ emitter. In order to recognize the origin of such emission we must then analyze the time decay of the line and identify it with the lifetime of a specific radioisotope.
In Figure 8, we recognize two different decay slopes. The first corresponds to a half-life T 1/2 = 20.4 min and the second one to T 1/2 = 109.8 min. This allows to identify the first one as the decay of 11C and the second one as the decay of 18F. 11C decays as follows:
$$\begin{align}{}^{11}{\mathrm{C}}\to {\;}^{11}\mathrm{B}+{\mathrm{e}}^{+}+\nu_\mathrm{e},\end{align}$$
Figure 8 Count decay in time of the 511 keV line from the irradiated BNH6 (ammonia borane) pellet. The time 0 in this graph corresponds to the beginning of the measurement with the HPGe detector, typically about half an hour after the end of the irradiation (due to the time needed to vent the chamber, extract the sample and insert it in the HPGe detector).
and is produced by the following reaction:
$$\begin{align}p\;{+}^{11}\mathrm{B}{\to}^{11}{\mathrm{C}}+n - 2.765\;\mathrm{MeV}.\end{align}$$
18F decays as follows:
$$\begin{align}{}^{18}\mathrm{F}{\to}^{18}\mathrm{O}+{\mathrm{e}}^{+}+\nu_\mathrm{e},\end{align}$$
and it can either be produced by the following reaction
$$\begin{align}\alpha\;{+}^{14}\mathrm{N}{\to}^{18}{\mathrm{F}}+\gamma +4.415\;\mathrm{MeV}\end{align}$$
from the α-particles generated by the proton–boron fusion reaction reacting with the nitrogen in BNH6, or from the following reaction:
$$\begin{align}{}^{18}\mathrm{O}+p{\to}^{18}{\mathrm{F}}+n - 2.44\;\mathrm{MeV}\end{align}$$
from the impurities in the sample (i.e., absorbed water). Of course, the quantity of oxygen in our sample is much less than that of nitrogen; however, the flux of protons is much higher than the number of α-particles (usually in this kind of experiment the ratio between α-particles and protons is of the order of 10–4 [ Reference Margarone, Bonvalet, Giuffrida, Morace, Kantarelou, Tosca, Raffestin, Nicolaï, Picciotto, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Batani 12 , Reference Margarone, Morace, Bonvalet, Abe, Kantarelou, Raffestin, Giuffrida, Nicolai, Tosca, Picciotto, Petringa, Cirrone, Fukuda, Kuramitsu, Habara, Arikawa, Fujioka, D’Humieres, Korn and Batani 15 , Reference Bonvalet, Nicolaï, Raffestin, D’humieres, Batani, Tikhonchuk, Kantarelou, Giuffrida, Tosca, Korn, Picciotto, Morace, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Margarone 16 ]). Hence, in our case the most probable origin of 18F is from oxygen impurities (i.e., from water).
Let us note that in principle we could also observe the 511 keV from the decay of 13N, another β+ emitter that can either be produced by the reaction α + 10B ⟶ 13N + n + 1.06 MeV, or by the reaction p + 16O ⟶ 13N + α – 5.22 MeV. However, due to the very short lifetime of 13N (T 1/2 = 9.97 min) we could not see the signature of its decay in our measurements.
Starting from the graph in Figure 8 and the calibration line in Figure 3 we can evaluate the activity and number of produced 11C isotopes. Figure 8 shows that the number of counts recorded during 5 min is N
o
$\approx 3.4 \times 10^{4}$
at t = 0. At the photon energy of 511 keV, which is the same as the line from 22Na, the detection efficiency is as follows:
$$\begin{align}D=\frac{\mathrm{Activity}\;[\mathrm{kBq}]}{\mathrm{Counts}}\approx 0.0001,\end{align}$$
from which we recover an activity of 3.4
$\mathrm{kBq}$
obtained with 31 shots on target. The relation among activity, the decay constant
$\lambda$
, the lifetime
${T}_{1/2}$
and the number N of radioisotopes is as follows:
$$\begin{align}A= N\lambda, \kern5.039997em \lambda =\frac{0.693}{T_{1/2}},\end{align}$$
which for 11C gives
$\lambda =5.66\cdot {10}^{-4}$
s–1, from which the number of 11C radioisotopes can be estimated as follows:
$$\begin{align}{N}_{31\#}=6.0\times {10}^6.\end{align}$$
As specified before, this number corresponds to the beginning of the measurement with the HPGe detector, typically about half an hour after the end of the irradiation (due to the time needed to vent the chamber, extract the sample, etc.). By correcting for the decay rate, we see that the number of counts, which would be recorded just after the end of the irradiation, would increase by a factor
$\approx$
4.34, thereby yielding a count of
$\approx 1.48 \times 10^5$
. This corresponds to activity of
$\approx$
15 kBq.
In reality such number must also be corrected to take into account that the time needed to accumulate 31 shots was
$\approx$
1 h; therefore, there was a significant decay of 11C during the irradiation itself. The calculation, performed in Appendix A, shows that realizing the 31 shots in a very short time compared to the lifetime (T
1/2 = 20.4 min) would have provided an increase of a factor
$\approx 2.42$
, bringing the total production of 11C radioisotopes to
$\approx 6.4\times {10}^7$
and the total activity to
$\approx$
36 kBq.
Hence, we estimate that one laser shot thus produces about
$2\times {10}^6$
of 11C, or an activity of more than 1 kBq.
Another interesting question is how we compare the number of generated 11C isotopes and α-particles, that is, the number of fusion reactions taking place. This is relevant to establishing the capability of using γ-ray emission from 11C as diagnostics of hydrogen–boron fusion in addition to classical CR39 detectors. The number of created α-particles and 11C isotopes has been evaluated using simple Python software validated against the results of more complex Monte Carlo simulations (as described in Appendix B). The calculation uses the experimentally measured proton spectrum as input (the spectrum is shown in Appendix B).
This shows that in each laser shot
$\approx 0.97\times {10}^6$
of 11C particles generated, that is, the experimental result is indeed close to the calculation (within a factor of two).
The experimental evaluation of α-particle yield is more difficult being based on analysis of CR39 foils[
Reference Ingenito, Andreoli, Batani, Bonasera, Boutoux, Burgy, Cipriani, Consoli, Cristofari, De Angelis, Di Giorgio, Ducret, Giulietti and Jakubowska
22
,
Reference Consoli, De Angelis, Andreoli, Bonasera, Cipriani, Cristofari, Di Giorgio, Giulietti and Salvadori
23
,
Reference Kantarelou, Velyhan, Tchórz, Rosiński, Petringa, Cirrone, Istokskaia, Krása, Krus, Picciotto, Margarone and Giufrida
42
], which contains a certain degree of uncertainty and, of course, only measures the α-particles escaping the target. The number of escaping α-particles is evaluated in Appendix B and corresponds to
$\approx 1.2\times {10}^6$
particles exiting the target from the front side per laser shot, or about
$\approx 0.84\times {10}^6$
α-particles with energy of more than 1.57 MeV.
For comparison, the analysis of CR39 (see Appendix C) provides a number of 5
$\times$
10Reference Batani
5
α-particles with energy ≥1.57 MeV per solid angle and per laser shot. Assuming an isotropic generation over the 2π solid angle corresponding to the ‘front side’, we get an estimation of 3
$\times$
10Reference Belyaev, Krainov, Matafonov and Zagreev
6
α-particles of energy of more than 1.57 MeV. This number corresponds to what is measured when a 5 μm Al foil filter is placed in front of the CR39 detector. This filter transmits α-particles of energy of more than 1.57 MeV but prevents a significant contamination from other laser-accelerated ions.
The theoretical estimation is therefore a factor of 3 below the experimental one (the difference might be largely due to the hypothesis of isotropic generation over a 2π solid angle).
If we look at the ratio of 11C to α-particles (with energy >1.6 MeV), we see the following:
$$\begin{align}{\left(\frac{\alpha }{{}^{11}\mathrm{C}}\right)}_{\mathrm{exp}}&={\left(\frac{3\times {10}^6}{2\times {10}^6}\right)}_{\mathrm{exp}}\approx 1.5,\nonumber\\ {\left(\frac{\alpha }{{}^{11}\mathrm{C}}\right)}_\mathrm{cal}&={\left(\frac{0.84\times {10}^6}{0.97\times {10}^6}\right)}_\mathrm{cal}\approx 0.9.\end{align}$$
This shows that, within the limit of precision of the present experiment, the measured activity of 11C is in fair enough agreement with the measured α-particle yield and can indeed provide a way to estimate the total number of hydrogen–boron fusion reactions. The excess number of α-particles with respect to 11C might be possibly due to the fact that the CR39 measurement is somewhat polluted by the presence of other ions coming from the catcher[
Reference Scisciò, Petringa, Zhe, Rodrigues, Alonzo, Andreoli, Filippi, Consoli, Huault, Raffestin, Molloy, Larreur, Singappuli, Carriere, Verona, Nicolai, McNamee, Ehret, Filippov, Lera, Pérez-Hernández, Agarwal, Krupka, Singh, Lattuada, La Cognata, Guardo, Palmerini, Rapisarda, Batani, Cipriani, Cristofari, Di Ferdinando, Di Giorgio, De Angelis, Giulietti, Jun, Volpe, Giuffrida, Margarone, Batani, Cirrone, Bonasera and Consoli
27
]. As mentioned before, the theoretical evaluation from Appendix B predicts
$1.2\times {10}^6$
α-particles escaping the catcher from the front side and a total α-particle yield of 1.11
$\times$
10Reference Oliphant and Rutherford
7
, that is, in our experimental configuration about 90% of α-particles remain trapped inside the catcher. This is similar to what has already been shown by Scisciò et al.
[
Reference Scisciò, Petringa, Zhe, Rodrigues, Alonzo, Andreoli, Filippi, Consoli, Huault, Raffestin, Molloy, Larreur, Singappuli, Carriere, Verona, Nicolai, McNamee, Ehret, Filippov, Lera, Pérez-Hernández, Agarwal, Krupka, Singh, Lattuada, La Cognata, Guardo, Palmerini, Rapisarda, Batani, Cipriani, Cristofari, Di Ferdinando, Di Giorgio, De Angelis, Giulietti, Jun, Volpe, Giuffrida, Margarone, Batani, Cirrone, Bonasera and Consoli
27
] in the case of natural B catchers.
Taking into account that one fusion reaction releases three α-particles, we estimate that in this configuration we have produced
$\approx 4\times {10}^6$
hydrogen–boron fusion reactions per laser shot.
5 Radioisotope generation using calcium silicate
The irradiation of calcium can result in the production of scandium radioisotopes, which are very interesting for present, and even more for future, medical applications. In particular, 44Sc and 43Sc are β− emitters with a short lifetime (
$<4$
h) and with simultaneous emission of γ-rays only at relatively low energy. For these characteristics, they will produce little collateral damage to healthy cells and are therefore considered as optimal radiation sources for PET imaging.
In the experiment we irradiated calcium silicate samples (Ca2SiO4, sample size: 5 cm
$\times$
5 cm
$\times 0.$
5 cm). A thin layer of 11B was deposited on the samples using a PLD technique at Politecnico di Milano. The layer thickness was ≈3 μm and its atomic composition was approximately equal to 95%–96% 11B and 4%–5% O. More details about the PLD system and the characteristics of the boron films can be found in Refs. [43,44]. The goal of this layer was of course to absorb part of the incident proton flux and produce α-particles by the proton–boron fusion reactions. Such α-particles could then induce the formation of radioisotopes in calcium silicate.
The samples were placed behind the Al pitcher (6 μm) inclined by 12° with respect to the laser propagation axis, at a distance of 2 cm, and irradiated with 31 laser shots. After irradiation the sample was placed in the HPGe detector and acquisitions were done every 5 min (accumulating signal for 5 min). The accumulated spectrum is shown in Figure 9 in the range
$950-1700\;\mathrm{eV}.$
It shows the presence of several γ-ray lines from 44Sc and 48Sc. At lower energy we find the line at 511 keV, due to positron annihilation.
Figure 9 (Left) Recorded γ-ray spectrum at
$h\nu >950\;\mathrm{keV}.$
The line at 1669 keV corresponds to the simultaneous absorption of photons at 1157 keV and 511 keV. (Right) Decay of the emission line at 1157 keV with time.
Similar spectra have already been identified in the literature[ Reference Rotsch, Brown, Nolen, Brossard, Henning, Chemerisov, Gromov and Greene 45 – Reference Kaipov, Kosyak and Lysikov 47 ] (but not from laser-generated radioisotopes). As an additional proof, we measured the decay time of the line at 1157 keV, as shown in Figure 9 (right). The measured lifetime agrees well, within error bars, with the lifetime of 44Sc.
Scandium radioisotopes can be produced by irradiation of natural calcium with protons or α-particles, as shown in Table 2 [ 48 ].
Table 2 Production and decay chain for the scandium radioisotopes observed in our experiment.
44Sc is produced by the reaction of protons with 44Ca. In our case, the isotope 48Sc is likely produced also by protons rather than α-particles, first of all because, as written before, in laser-driven proton–boron fusion experiments the ratio of produced α-particles to protons is
$\approx$
10–4, and secondly because 48Ca is much more abundant than 46Ca, representing only 0.004% of natural calcium (see Table 3).
Table 3 Abundance of stable isotopes of calcium (except 48Ca, which is practically stable with a lifetime of 6.4
$\times$
10Reference Batani, Boutoux, Burgy, Jakubowska and Ducret
19
years).
As done for 11C we can evaluate the number of produced radioisotopes starting from the recorded γ-ray spectra. The number of counts recorded at the initial time (see Figure 9) is
$\approx 200.$
In this case since the lifetime of 44Sc is not as short as that of 11C, the corrections taking into account the decay time are not so important. The 200 counts obtained at the beginning of the measurement with the HPGe correspond to
$\approx$
226 counts half an hour before (i.e., at the end of the irradiation) and the correction taking into account the irradiation time implies an additional factor of
$\approx 1.05$
(see Appendix A). This would bring the total number of counts to
$\approx$
240.
The detection efficiency approximately corresponds to that obtained from 22Na at energy of 1274.5 eV (which is close to the 1157 keV line of 44Sc), that is,
$D\approx$
0.00027 (for 5 min accumulation), which corresponds to an activity
$A$
as follows:
$$\begin{align}A\;\left[\mathrm{kBq}\right]=D\times \mathrm{Counts}\approx 0.065\;\mathrm{kBq},\end{align}$$
with 31 shots on target. The decay constant for 44Sc is
$\lambda =4.76\times {10}^{-5}$
s–1, from which we get the following:
$$\begin{align}{N}_{31\#}=\frac{65}{4.76\times {10}^{-5}}\approx 1.4\times {10}^6.\end{align}$$
Hence, we can estimate a production of
$\approx 4.5\times {10}^4$
radioisotopes per shot.
We also looked for the signature of 43Sc, which emits a γ-ray line at 373 keV. The line was indeed present but it was very weak and superimposed on the Compton shoulder. In order to get an estimation, we had to remove the contribution of the Compton shoulder and smooth the data to remove noise. The original spectrum and the treated one are shown in Figure 10.
Figure 10 (Left) Accumulated γ-ray spectrum from the Ca2SiO4 sample in the range 350 keV <
$h\nu <500\;\mathrm{eV}.$
43Sc and 7Be γ-ray emission lines are superimposed to the Compton shoulder. (Right) The same after removing the Compton shoulder and after smoothing. The sample was irradiated for 33 min, and the measurement was accumulated over 225 min.
The low production of 43Sc in comparison to 44Sc is explained by the lower abundance of 43Ca in comparison to 44Ca within the natural calcium material used in the experiment. In addition, the production of 43Sc from α-particles is negligeable, again because of the much smaller number of α-particles with respect to protons, which balances the fact that 43Ca is only 0.135% of natural calcium (see Table 3).
We also observed a weak emission of γ-ray lines at 477 keV from the isotope 7Be, which is produced by the reaction p + 10B
$\to$
7Be + α + 1.15 MeV (T
1/2 = 53.22 days).
6 Future perspectives
We have successfully shown the production of radioisotopes in laser-driven experiments. This can be useful potentially for the possibility of producing radioisotopes of interest for medical applications and also for diagnostics purposes (i.e., to infer the total number of nuclear reactions taking place in the target). In this case, of course, we need to greatly improve the yields from laser experiments in order to become competitive with existing tools for radioisotope production.
Currently radioisotopes are produced either in nuclear reactors (by neutrons) or in dedicated cyclotron systems (by protons). A few specific radioisotopes are also produced using large heavy ion cyclotron systems (such as the cited ARRONAX or U-120M), which accelerate He nuclei, that is, α-particles. For instance, ARRONAX can produce a current of 70 μA of α-particles. A current of 10 μA corresponds to a flux of α-particles:
$$\begin{align}10\;\mu \mathrm{A}\to \kern0.48em {N}_{\alpha }\ [\mathrm{s}^{-1}]=\frac{10^{-5}\;\mathrm{C}/\mathrm{s}}{2\times 1.6\times {10}^{-19}\ \mathrm{C}}=3\times {10}^{13}\;\mathrm{s}^{-1}.\end{align}$$
Reaching performances of the order of a few 10 μA of α-particles with lasers is extremely challenging. Today, laser experiments show a maximum of 10Reference Giuffrida, Belloni, Margarone, Petringa, Milluzzo, Scuderi, Velyhan, Rosinski, Picciotto, Kucharik, Dostal, Dudzak, Krasa, Istokskaia, Catalano, Tudisco, Verona, Jungwirth, Bellutti, Korn and Cirrone
11
α-articles per sr per shot or about a maximum of
${10}^{12}$
α-particles per shot[
Reference Giuffrida, Belloni, Margarone, Petringa, Milluzzo, Scuderi, Velyhan, Rosinski, Picciotto, Kucharik, Dostal, Dudzak, Krasa, Istokskaia, Catalano, Tudisco, Verona, Jungwirth, Bellutti, Korn and Cirrone
11
,
Reference Margarone, Bonvalet, Giuffrida, Morace, Kantarelou, Tosca, Raffestin, Nicolaï, Picciotto, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Batani
12
]. In order to be comparable, such a laser-driven source must then work at a repetition rate as follows:
$$\begin{align}f=\frac{3\times {10}^{13}\;\mathrm{per\ second}}{10^{12}\ \mathrm{per\ shot}}=30\;\mathrm{Hz}.\end{align}$$
This requires developing a new generation of
$\approx$
100 Hz petawatt laser systems. Although this is a challenging goal, laser technology is indeed already moving in this direction[
49
]. Also notice that in our experiment, the α-particle yield was much lower than ‘record’ yields.
In reality, even operating lower performing laser-driven α-particle sources could still be interesting if laser-driven sources are cheaper and more compact so as to be installed in more medical centers and be more diffused in the territory (this is particularly important for short-life radioisotopes, which are the most interesting for medical applications), serving as ‘in-hospital’ isotope manufacturing for fast administration of short-lived isotopes.
At the same time, in order to increase the number of produced radioisotopes for laser shots, we need to carefully choose target materials. For instance, while in our experiment we produce
$4.5 \times 10^{4}$
of 44Sc radioisotopes per shot with natural Ca (a mixture of 44Ca and other Ca isotopes), we could increase the production by using a target containing only 44Ca. This is likely to increase radioisotope production by a factor 1/2.09%
$\approx$
50. An even larger increase would be obtained by using a pure 44Ca target instead of a calcium silicate.
It is also clear that for radioisotopes produced by α-particles, a three-step process (pitcher
$\to$
catcher
$\to$
target material) is very ineffective. Many particles are lost at each step, and, above all, most α-particles are confined in the catcher due to the very short propagation range in solid density matter (
$\approx$
micrometers). We therefore need to use mixed targets, where boron (to produce α-particles from protons) and the target material (generating the radioisotopes) are in direct contact. Concerning Sc radioisotopes, interesting materials are indeed calcium silicate or even better calcium hexaboride (B6Ca).
The other important question concerns the purity of the produced radioisotopes. For instance, in the case of Sc, it would be preferable to produce a single radioisotope rather than a mixture of 44Sc, 48Sc and 43Sc. 44Sc and 43Sc are both used in medicine as a source for PET imaging. However, 43Sc is often considered as the ‘radioisotope of the future’ in PET because of its short lifetime and the absence of simultaneous γ-emission at energies high enough to possibly cause radiation damage to human cells (43Sc emits γ-rays at 373 keV, which is even lower than γ-rays emitted by 44Sc at 1157 keV). Pure 43Sc could be obtained by irradiating natural calcium with α-particles. Unfortunately, in experiments with laser-driven α-particle sources, the α-particles are always accompanied by a much larger flux of protons that, as in the present experiment, can produce 44Sc by reaction with the isotope 43Ca. Indeed, although 43Ca is only 2.09% of natural calcium, there are far fewer α-particles than protons, so this reaction channel is dominant. Using isotopically pure 40Ca would prevent this; however, 40Ca is present at 96.9% in natural Ca and it is very difficult to get isotopic concentration above 99.5%[ 50 ].
Instead, pure 44Sc could be obtained using protons on isotopically pure 44Ca (the production of 43Sc by the 2n reaction being largely minor). In this case, one should consider that the present compact cyclotrons used for production of medical radioisotopes have currents of the order of 100–150 μA, which is a factor of
$\approx$
2 above the α-particle current produced by ARRONAX. However, as we said before, the ratio of α-particles to protons in laser-driven experiments for the production of particle sources is typically a factor
$\approx$
10Reference Kimura, Anzalone and Bonasera
4
in favor of protons. To produce 100 μA, a laser that works at 100 Hz repetition frequency should accelerate
$\approx 6 \times 10$
Reference Margarone, Bonvalet, Giuffrida, Morace, Kantarelou, Tosca, Raffestin, Nicolaï, Picciotto, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Batani
12
protons per laser shot. If the protons have an average energy of 10 MeV, the total energy in the proton beam is about 1 J, which could imply a laser energy per shot of 10 J assuming a laser-to-proton conversion efficiency of 10%. Indeed, these numbers represent a reasonable (although optimistic) extrapolation of current performances, which shows how laser-driven proton sources could also be interesting for the production of medical radioisotopes.
7 Conclusions
In our experiment, we have successfully identified γ-ray lines from multiple radioisotopes created by irradiation using laser-generated α-particles or protons. These includes 43Sc, 44Sc, 48Sc, 7Be, 11C and 18F. With respect to our previous work[ Reference Rodrigues, Bonasera, Scisciò, Pérez-Hernández, Ehret, Filippi, Andreoli, Huault, Larreur, Singappuli, Molloy, Raffestin, Alonzo, Rapisarda, Lattuada, Guardo, Verona, Consoli, Petringa, McNamee, La Cognata, Palmerini, Carriere, Cipriani, Di Giorgio, Cristofari, De Angelis, Cirrone, Margarone, Giuffrida, Batani, Nicolai, Batani, Lera, Volpe, Giulietti, Agarwal, Krupka, Singh and Consoli 28 ], here we focused on radioisotopes of medical interest (43Sc, 44Sc) and we provided an evaluation on how laser-driven sources could become competitive for radioisotope production. We also described the HPGe detector and the calibration procedure in detail, and we have also shown a fairly good agreement between data obtained from γ-ray spectroscopy and other diagnostics (CR39). This shows the possibility of using γ-ray spectroscopy as a reliable diagnostic tool to measure the activation of target materials and reaction rates. This can be important, for instance for proton–boron fusion experiments where measuring α-particle yields with CR39 has always been an issue.
We have also shown the production of
$\approx$
6 × 10Reference Belyaev, Krainov, Matafonov and Zagreev
6
of 11C radioisotopes and
$\approx$
5 × 10Reference Kimura, Anzalone and Bonasera
4
of 44Sc radioisotopes per laser shot. Again, a proper choice of target material can considerably increase the production rate: this could be pure 11B for 11C production or pure 44Ca for 44Sc production. This result can open the way to develop laser-driven radiation sources of radioisotopes for medical applications.
In this context in the future, we will need to perform experiments that produce a separable quantity of radioisotopes (first step), and that match the doses (MBq) used in medicine (second step). These objectives can be achieved by accumulating a much larger number of shots (i.e., working at a high repetition rate), by optimizing laser parameters and by developing new target materials (e.g., for radioisotopes produced by α-particle targets mixing boron and the precursor material of the radioisotope to be produced).
Appendix A: Effect of decay
In the case of short-living elements, one must take into account not only the decay during the time
${\tau}_1$
between the end of the irradiation and the beginning of the measurements with the γ-ray spectrometer, but also the decay during the time needed to do all the laser shots.
This is important for the case of 44Sc with a lifetime T
1/2 = 3.97 h = 238.2 min and even more for 11C with a lifetime T
1/2 = 20.4 min. In comparison, typically
${\tau}_1\approx$
30 min. In addition, we were doing a laser shot every 2 min (=
${\tau}_2),$
which means that the total time needed to perform 30 shots is 1 h (=
${\tau}_3)$
.
In this case if
${N}_\mathrm{o}$
is the number of radioisotopes created by a single laser shot, the number of radioisotopes with decay time
$\tau$
present at the end of the shot series will be, counting from the first to the last shot, as follows:
$$\begin{align}N&={N}_\mathrm{o}{e}^{-\left({\tau}_3/\tau \right)}\,+\,{N}_\mathrm{o}{e}^{-\left(\left({\tau}_3-{\tau}_2\right)/\tau \right)}\,+\,{N}_\mathrm{o}{e}^{-\left(\left({\tau}_3-2{\tau}_2\right)/\tau \right)}+\dots\nonumber\\&\quad +\, {N}_\mathrm{o}{e}^{-\left(\left({\tau}_3-n{\tau}_2\right)/\tau \right)}\nonumber\\ {}&=\kern0.36em {N}_\mathrm{o}{e}^{-\left({\tau}_3/\tau \right)}\sum_{i=0}^{n-1}{e}^{\left(\;i\;{\tau}_2/\tau \right)}=\kern0.36em {N}_\mathrm{o}{e}^{-\left({\tau}_3/\tau \right)}\sum_{i=0}^{n-1}{e}^{{\left({\tau}_2/\tau \right)}^i},\end{align}$$
where
$\tau$
is related to the lifetime by the relation
$\tau ={T}_{1/2}/0.693=1/\lambda$
. The last factor is the geometrical sum of terms with ratio
${e}^{\left({\tau}_2/\tau \right)}$
, and therefore the result is
$$\begin{align}\frac{1-{e}^{{\left({\tau}_2/\tau \right)}^n}}{1-{e}^{\left({\tau}_2/\tau \right)}}=\frac{1-{e}^{\left({n\tau}_2/\tau \right)}}{1-{e}^{\left({\tau}_2/\tau \right)}}=\frac{1-{e}^{\left({\tau}_3/\tau \right)}}{1-{e}^{\left({\tau}_2/\tau \right)}}\end{align}$$
since of course
${n\tau}_2={\tau}_3$
. Notice that for
${\tau}_2\to 0$
(or equivalently for long-life radioisotopes for with
$\tau \gg {\tau}_3>{\tau}_2$
) we get the following:
$$\begin{align}\sum_{i=0}^{n-1}{e}^{{\left({\tau}_2/\tau \right)}^i}=\sum_{i=0}^{n-1}1=n,\end{align}$$
and in this case,
$$\begin{align}N\to n\;{N}_\mathrm{o}\equiv {N}_\mathrm{HRR},\end{align}$$
since indeed also
${\tau}_3\to 0$
. Indeed,
$$\begin{align}\frac{1-{e}^{\left({n\tau}_2/\tau \right)}}{1-{e}^{\left({\tau}_2/\tau \right)}}\approx \frac{1-\left(1+{n\tau}_2/\tau \right)}{1-\left(1+{\tau}_2/\tau \right)}=\frac{-{n\tau}_2/\tau }{-{\tau}_2/\tau}=n.\end{align}$$
We can therefore compare the actual number of measured radioisotopes
$N$
to the number of radiosiotopes
${N}_\mathrm{HRR},$
which would be obtained using a high-repetition laser in which
${\tau}_3\approx 0.$
The ratio is given by the following:
$$\begin{align}\frac{\kern0.24em {N}_\mathrm{HRR}}{N}=\frac{n{N}_\mathrm{o}}{\kern0.36em {N}_\mathrm{o}{e}^{-\left({\tau}_3/\tau \right)}}\cdot \frac{1-{e}^{\left({\tau}_2/\tau \right)}}{1-{e}^{\left({\tau}_3/\tau \right)}}=n{e}^{\left({\tau}_3/\tau \right)}\cdot \frac{1-{e}^{\left({\tau}_2/\tau \right)}}{1-{e}^{\left({\tau}_3/\tau \right)}}.\end{align}$$
Now taking into account the decay during the time
${\tau}_1$
between the end of the irradiation and the beginning of the measurements, this number must also be increased by the factor
${N}_\mathrm{o}{e}^{\left({\tau}_1/\tau \right)}.$
Finally, in the case of 44Sc, we have the following:
$$\begin{align}n&=30,\ {\tau}_3=30\;{\min},\ {\tau}_2=1\;{\min},\ \tau =343.7\;{\min},\nonumber\\ {}\frac{\kern0.24em {N}_\mathrm{HRR}}{N}&=30\times {e}^{\left(30/344\right)}\frac{1-{e}^{\left(1/344\right)}}{1-{e}^{\left(30/344\right)}}\nonumber\\&=30\times 1.09\times \frac{-0.00291}{-0.091}=1.05,\end{align}$$
which is a moderate increase.
Instead, for the case of 11C for which T
1/2 = 20.4 min (
$\tau =$
29.44 min), we have the following:
$$\begin{align}{c}n&=30,\ {\tau}_3=60\;{\min},\ {\tau}_2=2\;{\min},\ \tau =29.44\;{\min},\nonumber\\ {}\frac{\kern0.24em {N}_\mathrm{HRR}}{N}&=30\times {e}^{\left(60/29.44\right)}\frac{1-{e}^{\left(2/29.44\right)}}{1-{e}^{\left(60/29.44\right)}}\nonumber\\&=30\times 7.676\times \frac{-0.0703}{-6.676}=2.42.\end{align}$$
This shows that delivering 30 shots in a short time instead of 1 h would have more than doubled the number of 11C radioisotopes. Indeed, this is technically feasible because PW lasers such as VEGA-3 can in principle work at 1 Hz repetition frequency (provided they are also coupled to a high-repetition-rate target assembly), and delivering 30 shots would then require only half a minute.
Appendix B: Calculation of reaction products
A calculation of the number of nuclear reactions taking place in the catcher can be performed using Monte Carlo simulations codes, such as FLUKA or GEANT4. In order to allow for a faster and qualitatively correct estimation, we have developed a simpler software tool in Python[ Reference Larreur, Carrière, Volpe and Batani 51 ], which can be used to perform yield estimation for pitcher–catcher experiments, and which has been validated against the results of more complex (and time-consuming) Monte Carlo simulations.
This software, named FISP (for Fast Ion Spectrum Propagator), works in one dimension using the reaction cross-section and stopping power data, and assumes as input data the experimental spectrum of incident ions (in our case TNSA accelerated protons). This proton spectrum, divided into many quasi-monoenergetic contributions (bins), is propagated into the catcher target divided into infinitesimal slices.
In each slice, the energy deposited in the catcher from each bin in the spectrum is calculated according to the stopping power of the material at the corresponding bin energy. FISP uses Bethe’s formula at high energies and a constant slowing down approximation at low energies. The limit is dynamically set by the code at the value of the peak of the stopping power curve calculated using Bethe’s formula. The deposited energy is then removed from the initial energy to calculate the new bin energy. Any spectrum bin for which the energy falls to zero is removed from the spectrum, which is equivalent to particles stopping.
At the same time, for each energy bin and in each target slice, FISP calculates the number of reactions between the propagating protons and the different atoms in the catcher material. This is done using cross-section data.
FISP is not a Monte Carlo code: it does not calculate the behavior of individual particles and repeat the calculations for many particles. Instead, for a population of particles it calculates the exact proportion of particles that will (or will not) react. Once the number of reactions is calculated, FISP removes one incident ion per reaction from the incident spectrum. The new population of ions created by the reaction can eventually also be propagated into the target following a similar procedure. Since the code is one-dimensional (1D), the generated ions can only propagate back or forward. This process is repeated until the last slice of the target is allowed to calculate the spectrum of particles that exit the target on the front and on the back side. While clearly the 1D approximation does not allow one to calculate angular distributions, we verified that it does not drastically affect the total number of generated particles nor the number of particles exiting the target.
Here we will detail the FISP calculations for the BNH6 target with thickness of 1.2 mm. The input proton spectrum used in the calculations is shown in Figure 11. Two experimental spectra (to show shot-to-shot variations in the experiment) are shown and compared to a simulated spectrum.
Figure 11 Proton spectrum obtained with the SMILEI PIC code and comparison with the experimental proton spectra measured with the TP.
The experimental spectra show a proton cut-off energy of the order of 15–17 MeV. The simulated spectra have been obtained by particle-in-cell (PIC) simulations using the code SMILEI[
Reference Derouillat, Beck, Pérez, Vinci, Chiaramello, Grassi, Fl, Bouchard, Plotnikov, Aunai, Dargent, Riconda and Grech
52
] assuming a pre-plasma density scale length of 0.1 μm as produced by the laser pedestal[
Reference Maire, Abgrall, Breil and Ovadia
53
]. The spectra are shown per unit solid angle. The total number of protons has then been inferred by assuming a typical opening angle of the proton beam of
$\approx$
30° (half width).
The stopping power for BNH6 has been calculated, as stated, using Bethe’s formula with the correct density of BNH6 and an effective potential corresponding to the average chemical composition. The cross-section data for hydrogen–boron fusion and for the generation of neutrons and 11C isotopes are taken from Ref. [54], and are shown in Figure 12.
Figure 12 The cross-section data for hydrogen–boron fusion and for the generation of neutrons and 11C isotopes.
Using such data, FISP calculates the total number of particles generated in the target, together with their spectra. Table 4 shows the total number of particles generated, including those unable to exit the target. Figure 13 shows the spectra of particles escaping the targets on the front and rear sides. In our case only about 1/10 of the generated α-particles are able to escape the target (or 1.2 × 10Reference Belyaev, Krainov, Matafonov and Zagreev 6 ), which is of course due to the very short penetration range of α-particles in solid density matter.
Table 4 Reaction products from ammonia borane.
Figure 13 The spectra of particles escaping the targets on the front and rear sides (results from FISP).
The number of 11C isotopes and neutrons is the same since they are created by the same nuclear reaction. As for comparing the number of 11C and α-particles, Figure 12 shows that the maximum cross-section for the two reactions is similar (
$\approx$
1 barn), but while the hydrogen–boron fusion cross-section becomes already significant at energies as low as
$\approx 100$
keV (and reaches its maximum at
$\approx 600$
keV), the reaction generating 11C requires proton energy to be more than 2.765 MeV[
54
].
This means that low-energy protons are effective in inducing particle generation, but do not contribute to generating 11C. Hence, because of the low-energy part of proton spectrum, we expect that the number of 11C isotopes is much smaller than that of α-particles. Indeed, from the spectrum in Figure 11 we can calculate the total number of protons (per unit solid angle) of
$\approx$
2.1
$\times$
10Reference Margarone, Bonvalet, Giuffrida, Morace, Kantarelou, Tosca, Raffestin, Nicolaï, Picciotto, Abe, Arikawa, Fujioka, Fukuda, Kuramitsu, Habara and Batani
12
and the number of protons with E > 2.765 MeV, which is
$\approx$
1.9
$\times$
10Reference Giuffrida, Belloni, Margarone, Petringa, Milluzzo, Scuderi, Velyhan, Rosinski, Picciotto, Kucharik, Dostal, Dudzak, Krasa, Istokskaia, Catalano, Tudisco, Verona, Jungwirth, Bellutti, Korn and Cirrone
11
. Hence, there is a factor of
$\approx$
10 between the two populations. Now, the number of hydrogen–boron fusion reactions from Table 4 is
$\approx$
4
$\times$
10Reference Belyaev, Krainov, Matafonov and Zagreev
6
(one reaction produces 3 α-particles), which is exceeding by a factor of
$\approx$
4 the production of 11C. The remaining difference is due to the details of the cross-sections.
Appendix C: CR39 measurements for ammonia borane
Solid-state nuclear track detectors (CR39) have been used as detectors of α-particle generation. These plastic foils are exposed to the flux of particles generated from the interaction. The incoming radiation produces local damages by breaking of the long polymer chains. Along these damaged regions, the material is more susceptible to chemical attack, and, after a proper etching, holes become visible. These tracks can be properly characterized by microscope imaging providing information on particle energy and on type. For energies above approximately 1 MeV, the hole size increases with the duration of the etching procedure and decreases when the α-particle energy increases[ Reference Kantarelou, Velyhan, Tchórz, Rosiński, Petringa, Cirrone, Istokskaia, Krása, Krus, Picciotto, Margarone and Giufrida 42 ]. In our experiment[ Reference Huault, Carrière, Larreur, Nicolaï, Raffestin, Singappuli, D’Humieres, Dubresson, Batani, Cipriani, Filippi, Scisciò, Verona, Giuffrida, Kantarelou, Stancek, Boudjema, Lera, Pérez-Hernández, Volpe, Rodríguez Frías, Bonasera, Rodrigues, Ramirez Chavez, Consoli and Batani 38 ], after irradiation, the plastic polymer is etched in a caustic solution (6 mol/L NaOH at 70°C for 1–2 h).
In our experiment we used several CR39 foils placed in various positions. However, here we only describe the results obtained with the CR39 detector placed behind the TNSA shielding, as shown in Figure 1. This shield prevented protons and other ions being directly emitted from the pitcher from reaching the CR39. However, in addition to α-particles, other ions can be emitted from the catcher as a consequence of other nuclear reactions and, also, protons and ions from the pitcher can be scattered from the catcher and reach the CR39 detector. These can result in the production of holes in the etched CR39, which cannot easily be discriminated from those produced by α-particles. For this reason, half of the CR39 was covered with a 5 μm Al foil. The goal of this Al foil was to stop ions that can arrive at the detector. However, it also filtered all α-particles with energies of less than 1.57 MeV.
Figure 14 shows a histogram representing the number of holes (i.e., the number of particles) versus hole diameter obtained from the analysis of CR39 foils corresponding to the irradiation of ammonia borane. Here, we identify the small holes as due to protons, while larger holes correspond to α-particles and heavier ions. These larger holes appear as a second peak in Figure 14, between 1.1 and 2.6 μm for 1 h etching and between 2 and 3.6 μm for 2 h etching. These correspond to α-particle energies from approximately 0 up to approximately 3.2 MeV. The correspondence between the track diameter and α-particle energy follows an in-house calibration performed using the AIFIRA accelerator in Gradignan and a plutonium source[ 55 ]. The limits of applicability of such identification methodology are described in detail by Scisciò et al.[ Reference Scisciò, Petringa, Zhe, Rodrigues, Alonzo, Andreoli, Filippi, Consoli, Huault, Raffestin, Molloy, Larreur, Singappuli, Carriere, Verona, Nicolai, McNamee, Ehret, Filippov, Lera, Pérez-Hernández, Agarwal, Krupka, Singh, Lattuada, La Cognata, Guardo, Palmerini, Rapisarda, Batani, Cipriani, Cristofari, Di Ferdinando, Di Giorgio, De Angelis, Giulietti, Jun, Volpe, Giuffrida, Margarone, Batani, Cirrone, Bonasera and Consoli 27 ].
Figure 14 Histogram obtained from CR39 in the case of irradiation of the ammonia borane target. Here the CR39 was covered by a 5 μm Al filter.
Finally, the summation of this α-particle peak (for both 1 and 2 h etchings) provides a number of
$\approx$
5
$\times$
10Reference Batani
5
α-particles per solid angle and per laser shot in the region covered by the 5 μm Al foil. By comparison in the region without filters we get
$\approx$
7
$\times$
10Reference Belyaev, Krainov, Matafonov and Zagreev
6
α-particles per solid angle and per laser shot, which, as explained, is over-estimated because without the Al filter, the CR39 is directly exposed to the particle flux and, in addition to α-particles, other ions can also reach the detector. The number of 5
$\times$
10Reference Batani
5
α-particles of the energy of more than 1.57 MeV is instead more reliable, although some contamination from other laser-accelerated ions cannot be completely excluded[
Reference Scisciò, Petringa, Zhe, Rodrigues, Alonzo, Andreoli, Filippi, Consoli, Huault, Raffestin, Molloy, Larreur, Singappuli, Carriere, Verona, Nicolai, McNamee, Ehret, Filippov, Lera, Pérez-Hernández, Agarwal, Krupka, Singh, Lattuada, La Cognata, Guardo, Palmerini, Rapisarda, Batani, Cipriani, Cristofari, Di Ferdinando, Di Giorgio, De Angelis, Giulietti, Jun, Volpe, Giuffrida, Margarone, Batani, Cirrone, Bonasera and Consoli
27
]. Assuming an isotropic generation over the 2π solid angle corresponding to the ‘front side’, we can estimate 3
$\times$
10Reference Belyaev, Krainov, Matafonov and Zagreev
6
α-particles of the energy of more than 1.57 MeV.
Acknowledgements
We thank the Laser Division and Radioprotection, the Engineering and TIC areas and the Managing divisions of the CLPU for their valuable support. We thank Chris Spindloe from Scitech Precision Ltd., UK, for providing the ammonia borane targets. We also acknowledge the Unidad de Investigación Consolidada (UIC 167), Junta de Castilla y León Grant No. CLP087U16.
This work has been supported by COST (European Cooperation in Science and Technology) through Action CA21128 PROBONO (PROton BOron Nuclear Fusion: from energy production to medical applicatiOns). It also has received funding from the European Union’s 2020 research and innovation program under grant agreement No. 101008126 (RADNEXT project) and from the United States Department of Energy under grant #DEFG02-93ER40773.
SMILEI simulations were performed thanks to granted access to the HPC resources of TGCC under allocation No. 2023-A0140514117 made by GENCI. We also acknowledge the financial support of the IdEx University of Bordeaux/Grand Research Program ‘GPR LIGHT’ and of the Graduate Program on Light Sciences and Technologies of the University of Bordeaux. L.G. and V.K. acknowledge the support of the Czech Science Foundation through grant No. GACR24-11398S.
Finally, we acknowledge the support of HB11 Energy, Ltd., Australia, through its Collaborative Science Program. H.L. and M.H. acknowledge the direct support of HB11.
Open access
