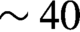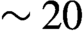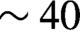1 Introduction
Radiative shocks are formed when radiative losses from the shock can modify its structure. This occurs when the radiative energy flux is comparable to the kinetic energy flux at the shock front. In this regime, radiation can modify both the pre- and post-shock regions. Radiative effects increase with the shock speed due to stronger post-shock heating and, in a first approximation for typical experimental conditions, radiative effects start playing a role at shock velocities of tens to hundreds of kilometres per second and gas pressures of ![]() $\sim 0.1$–1 bar[Reference Drake1]. With present-day laser facilities it is possible to reach such shock speeds by compressing and focusing the laser energy into a solid (e.g., a piston) or gas target. This has been done in a number of different laser facilities with a variety of energies, intensities (typically
$\sim 0.1$–1 bar[Reference Drake1]. With present-day laser facilities it is possible to reach such shock speeds by compressing and focusing the laser energy into a solid (e.g., a piston) or gas target. This has been done in a number of different laser facilities with a variety of energies, intensities (typically ![]() $\gtrsim$1014 W/cm2) and configurations, such as point explosions in a gas background, shock tubes and gas cells (a recent review can be found in Ref. [Reference Drake2]).
$\gtrsim$1014 W/cm2) and configurations, such as point explosions in a gas background, shock tubes and gas cells (a recent review can be found in Ref. [Reference Drake2]).
Recent works have looked at bridging the gap between experiments and theory/numerical simulations of radiative shocks[Reference Mabey, Michel, Albertazzi, Falize, Charpentier and Koenig3] and applications to astrophysics[Reference Mabey, Albertazzi, Rigon, Marqués, Palmer, Topp-Mugglestone, Perez-Martin, Kroll, Brack, Cowan, Schramm, Falk, Gregori, Falize and Koenig4]. In particular, recent experiments have looked at the interaction of a piston-driven shock with an obstacle[Reference Michel, Falize, Albertazzi, Rigon, Sakawa, Sano, Shimogawara, Kumar, Morita, Michaut, Casner, Barroso, Mabey, Kuramitsu, Laffite, Van Box Som, Gregori, Kodama, Ozaki, Tzeferacos, Lamb and Koenig5, Reference Michel, Albertazzi, Mabey, Rigon, Lefevre, Som, Barroso, Egashira, Kumar, Michaut, Ota, Ozaki, Sakawa, Sano, Falize and Koenig6]. However, several issues have led to difficulties making a complete bridge between simulations and experiments, for instance, the question of opacity for heavy gases (e.g., xenon) or the nature of the rise of instabilities and the role played by radiation. In addition, at higher velocity, temperature increases strongly and non-local thermodynamic equilibrium (non-LTE) effects start to play a role[Reference Rodríguez, Espinosa, Gil, Stehlé, Suzuki-Vidal, Rubiano, Martel and Mínguez7]. It is, therefore, of key importance to continue experimental efforts to obtain more experimental data to be compared with theoretical works.
The experiments presented here use the Shenguang-II (SG-II) laser to drive shocks via piston action from a foil attached to one of the ends of a gas-cell target. Although the SG-II laser has been operational for many years, future improvements planned for this facility in the coming years make these first experiments critical for planning and testing future experimental campaigns.
The targets are characterized by a large internal volume and field of view to probe the dynamics of the shock as a function of time without any shock–wall interactions. This configuration is similar to the first experiments performed on the Orion laser, where shocks were driven in xenon[Reference Suzuki-Vidal, Clayson, Stehlé, Swadling, Foster, Skidmore, Graham, Burdiak, Lebedev, Chaulagain, Singh, Gumbrell, Patankar, Spindloe, Larour, Kozlová, Rodriguez, Gil, Espinosa, Velarde and Danson8] and neon[Reference Clayson, Suzuki-Vidal, Lebedev, Swadling, Stehlé, Burdiak, Foster, Skidmore, Graham, Gumbrell, Patankar, Spindloe, Chaulagain, Kozlová, Larour, Singh, Rodriguez, Gil, Espinosa, Velarde and Danson9] with similar laser energies and gas pressures. However, the SG-II targets have a larger diagnostic field compared with the Orion experiments and, through the use of argon, we aim to study the formation of spatial nonuniformities in the shocks which were only investigated preliminarily at Orion.
2 Experimental setup
The SG-II laser[Reference Zhu, Zhu, Li, Zhu, Ma, Lu, Fan, Liu, Zhou, Xu, Zhang, Xie, Yang, Wang, Ouyang, Wang, Li, Yang, Fan, Sun, Liu, Liu, Zhang, Tao, Sun, Zhu, Wang, Jiao, Ren, Liu, Jiao, Huang and Lin10] can drive up to eight beams with a pulse duration of 1 ns in two opposite directed groups of four beams. Thus, 4–8 beams were used depending on whether the experiment was aimed at producing single or counter-propagating shocks. The overall experimental setup is shown schematically in Figure 1(a) for a single shock target. The targets are similar for the case of counter-propagating shocks, where four additional beams are focused on a second piston placed opposite to the first. Detailed dimensions for both types of targets are shown in Figures 1(b) and 1(c).

Figure 1 (a) Schematic diagram of the experimental setup for a single shock target on the SG-II laser, with a similar configuration used for counter-propagating shocks. (b), (c) Cross-sections of single and counter-propagating shock targets.
The lasers driving each shock had a total energy of ![]() $\sim 1$ kJ, a top-hat temporal profile with a duration of
$\sim 1$ kJ, a top-hat temporal profile with a duration of ![]() $\sim 1$ ns and a frequency of 3
$\sim 1$ ns and a frequency of 3![]() $\omega$ (
$\omega$ (![]() $\lambda$ = 351 nm). The laser beams were focused to a nominal spot diameter of
$\lambda$ = 351 nm). The laser beams were focused to a nominal spot diameter of ![]() $\sim 300$ μm with a super-Gaussian spatial profile with n
$\sim 300$ μm with a super-Gaussian spatial profile with n ![]() $\sim$ 4–6. Measured laser parameters for the experiments are presented in Section 3. An external laser beam (the ninth beam) was used to drive X-ray backlighting onto a scandium foil to image the shock inside the gas cell side-on, that is, normal to the direction of propagation of the shock. The backlighter beam had an energy
$\sim$ 4–6. Measured laser parameters for the experiments are presented in Section 3. An external laser beam (the ninth beam) was used to drive X-ray backlighting onto a scandium foil to image the shock inside the gas cell side-on, that is, normal to the direction of propagation of the shock. The backlighter beam had an energy ![]() ${E}_{9 {\rm th}}\sim 500$ J and a pulse duration of
${E}_{9 {\rm th}}\sim 500$ J and a pulse duration of ![]() ${t}_{9 {\rm th}}\sim 1$ ns, with a spot size of
${t}_{9 {\rm th}}\sim 1$ ns, with a spot size of ![]() ${\varphi}_{9 {\rm th}}\sim 150$ μm at
${\varphi}_{9 {\rm th}}\sim 150$ μm at ![]() $3\omega$. In addition to the X-ray backlighter (XRBL) diagnostic, a filtered, time-integrated pinhole camera recorded the X-ray emission from the laser–piston interaction onto an image plate to estimate the size of the focal spot during each shot. An example of the results from the two diagnostics is presented in Figure 2.
$3\omega$. In addition to the X-ray backlighter (XRBL) diagnostic, a filtered, time-integrated pinhole camera recorded the X-ray emission from the laser–piston interaction onto an image plate to estimate the size of the focal spot during each shot. An example of the results from the two diagnostics is presented in Figure 2.

Figure 2 (a)–(c) View of the piston: (a) X-ray emission from the laser–piston interaction from a time-integrated pinhole camera diagnostic; (b) microscope image of the 1 mm diameter shock aperture and CH–Br/CH pistons; (c) lineout of (a) and Gaussian fit to estimate the laser spot size. (d), (e) Target view: field of view of the X-ray backlighting diagnostic of a single shock target and example of raw X-ray image result, respectively.
2.1 Target design
Gas-cell targets were designed for SG-II with two main purposes: (1) to provide a large ambient gas volume to allow the shocks to propagate without being subject to radiative or hydrodynamic interactions with the gas-cell walls; and (2) to maximize the XRBL diagnostic field of view in order to follow the evolution of the shocks for times up to 100 ns.
Two target designs (Figure 1(b)) were fielded on SG-II: a single shock target with a diagnostic window size (width ![]() $\times$ height) of 6 mm
$\times$ height) of 6 mm ![]() $\times$ 5 mm, and a counter-propagating shock target with a diagnostic window size of 3.6 mm
$\times$ 5 mm, and a counter-propagating shock target with a diagnostic window size of 3.6 mm ![]() $\times$ 5 mm. The window width of the counter-propagating shock targets was constrained by the maximum separation between the two opposite groups of long-pulse laser beams (i.e., 4 mm between focal spots). The gas-cell windows were sealed with a 25 μm thick polyimide foil, with a transverse distance between windows of 8 mm. The targets were positioned inside the chamber with a 3 mm diameter plastic rod glued at the top of each target, connected to a five-axis target positioner.
$\times$ 5 mm. The window width of the counter-propagating shock targets was constrained by the maximum separation between the two opposite groups of long-pulse laser beams (i.e., 4 mm between focal spots). The gas-cell windows were sealed with a 25 μm thick polyimide foil, with a transverse distance between windows of 8 mm. The targets were positioned inside the chamber with a 3 mm diameter plastic rod glued at the top of each target, connected to a five-axis target positioner.
The targets for SG-II were designed based on previous experiments on the Orion laser[Reference Spindloe, Wyatt, Astbury, Swadling, Clayson, Stehlé, Foster, Gumbrell, Charles, Danson, Brummitt and Suzuki-Vidal11], with several improvements implemented for SG-II: (1) a thinner, 0.2 mm thick frame between the piston and the edge of the diagnostic window to probe the early-time behaviour of the shock (cf. 1 mm for Orion). A drawback of decreasing the frame thickness was that this reduced the shielding that the target provided to prevent hard X-ray emission from the laser–piston interaction from contaminating the signal on the XRBL diagnostic. This meant the level of background noise in diagnostic images from these experiments was higher than the level observed previously on Orion. (2) A smaller, 1 mm diameter aperture for the piston was in contact with the gas (cf. 3–5 mm in Orion) to reduce the ‘swelling’ of the piston with gas-fill pressure inside the vacuum chamber. This helps to achieve a more consistent laser focal spot size during each shot. (3) Lastly, the SG-II targets were gas-filled in situ while inside the vacuum chamber, allowing for a faster shot turnaround and accurate gas-pressure measurement right before each shot. This gas-fill system was also used in previous experiments on the PALS laser[Reference Chaulagain, Stehl, Larour, Kozlov, Suzuki-Vidal, Barroso, Cotelo, Velarde, Rodriguez, Gil, Ciardi, Acef, Nejdl, de S, Singh, Ibgui and Champion12, Reference Singh, Stehl, Suzuki-Vidal, Kozlová, Larour, Chaulagain, Clayson, Rodriguez, Gil, Nejdl, Krus, Dostal, Dudzak, Barroso, Acef, Cotelo and Velarde13]. For the experiments presented here, argon with an initial gas pressure of ![]() ${P}_{\mathrm{Ar}}$ = 1 bar was used (
${P}_{\mathrm{Ar}}$ = 1 bar was used (![]() ${\rho}_{\mathrm{Ar}}$ = 1.67 mg/cm3).
${\rho}_{\mathrm{Ar}}$ = 1.67 mg/cm3).
The pistons for SG-II were made with a layer of 30 μm thick CH (on the laser-drive side, ![]() $\varphi \sim 3.2$ mm diameter, nominal mass density
$\varphi \sim 3.2$ mm diameter, nominal mass density ![]() ${\rho}_{\mathrm{CH}}$ = 0.9 g/cm3) followed by a 50 μm thick CH–Br layer (on the gas side, diameter
${\rho}_{\mathrm{CH}}$ = 0.9 g/cm3) followed by a 50 μm thick CH–Br layer (on the gas side, diameter ![]() $\varphi \sim 2$ mm, nominal mass density
$\varphi \sim 2$ mm, nominal mass density ![]() ${\rho}_{\mathrm{CH}-\mathrm{Br}}$ = 1.53 g/cm3). The brominated plastic layer helped to shield the gas from X-rays produced in the laser–CH interaction to reduce radiative pre-heating.
${\rho}_{\mathrm{CH}-\mathrm{Br}}$ = 1.53 g/cm3). The brominated plastic layer helped to shield the gas from X-rays produced in the laser–CH interaction to reduce radiative pre-heating.
2.2 XRBL diagnostic
A point-projection XRBL package was attached to the side of each target. It consisted of a 5 μm thick, 500 μm diameter scandium foil (a microdot) that was supported on a 100 μm thick tantalum substrate, glued to a 3D-printed acrylic frame that was aligned to the centre of the gas-cell window. The X-ray source size was constrained by a ![]() ${\varphi}_{\mathrm{PH}}=$ 20 μm diameter pinhole that was laser-cut into the Ta substrate. This pinhole was coated with a 9 μm parylene-N layer that served to prevent the closure of the pinhole by the plasma that was formed in the interaction between the backlighter beam and the Sc foil[Reference Kuranz, Blue, Drake, Robey, Hansen, Knauer, Grosskopf, Krauland and Marion14]. Laser-etched markings were added to the Ta substrate and the Sc foil to ensure accurate alignment during target manufacture and target alignment before each shot.
${\varphi}_{\mathrm{PH}}=$ 20 μm diameter pinhole that was laser-cut into the Ta substrate. This pinhole was coated with a 9 μm parylene-N layer that served to prevent the closure of the pinhole by the plasma that was formed in the interaction between the backlighter beam and the Sc foil[Reference Kuranz, Blue, Drake, Robey, Hansen, Knauer, Grosskopf, Krauland and Marion14]. Laser-etched markings were added to the Ta substrate and the Sc foil to ensure accurate alignment during target manufacture and target alignment before each shot.
The backlighter beam average laser parameters were an energy of ![]() ${E}_{9 {\rm th}}=478\pm 71$ J and a pulse duration
${E}_{9 {\rm th}}=478\pm 71$ J and a pulse duration ![]() ${t}_{9 {\rm th}}=1042\pm 188$ ps. The nominal spot size was
${t}_{9 {\rm th}}=1042\pm 188$ ps. The nominal spot size was ![]() $\sim$150 μm, giving an intensity of
$\sim$150 μm, giving an intensity of ![]() ${I}_{9 {\rm th}}\sim 2.6\times 1{0}^{15}$ W/cm2. Under these drive conditions, the X-ray emission from the interaction of the backlighter beam with the Sc foil is dominated by He-alpha emission with a photon energy of 4.3 keV[Reference Ruggles, Porter, Rambo, Simpson, Vargas, Bennett and Smith15], providing a quasi-monoenergetic source of X-rays to study the plasma in the shocks. The X-rays were recorded in a film pack with Fuji BAS-TR image plate, filtered with a 12.5 μm thick titanium filter and 2–3 layers of 8 μm thick aluminized polypropylene for optical and debris shielding. The XRBL package was placed at a distance of
${I}_{9 {\rm th}}\sim 2.6\times 1{0}^{15}$ W/cm2. Under these drive conditions, the X-ray emission from the interaction of the backlighter beam with the Sc foil is dominated by He-alpha emission with a photon energy of 4.3 keV[Reference Ruggles, Porter, Rambo, Simpson, Vargas, Bennett and Smith15], providing a quasi-monoenergetic source of X-rays to study the plasma in the shocks. The X-rays were recorded in a film pack with Fuji BAS-TR image plate, filtered with a 12.5 μm thick titanium filter and 2–3 layers of 8 μm thick aluminized polypropylene for optical and debris shielding. The XRBL package was placed at a distance of ![]() $p=21$ mm from the axis of the gas cell, with the image plate placed at a typical distance of
$p=21$ mm from the axis of the gas cell, with the image plate placed at a typical distance of ![]() $q\approx 226$ mm, thus resulting in a point-projection magnification of
$q\approx 226$ mm, thus resulting in a point-projection magnification of ![]() $M=\left(p+q\right)/p\approx 12$.
$M=\left(p+q\right)/p\approx 12$.
The spatial resolution of the XRBL was estimated by illuminating a vanadium grid attached to a target and fitting the resulting spatial profile to the convolution of the ideal point projection from the grid with a Gaussian function. This results in a resolution of ![]() $\sim 19$ μm, which is compatible with the size of the pinhole (
$\sim 19$ μm, which is compatible with the size of the pinhole (![]() ${\varphi}_{\mathrm{PH}}=20$ μm) and the geometrical resolution given by
${\varphi}_{\mathrm{PH}}=20$ μm) and the geometrical resolution given by ![]() $\delta \approx {\varphi}_{\mathrm{PH}}\left(M-1\right)/M\sim$18 μm[Reference Sinars, Gregorian, Hammer and Maron16]. The field of view of the XRBL diagnostic for a single shock target together with an example of results is shown in Figures 2(d) and 2(e). It should be noted that for the shock speed of
$\delta \approx {\varphi}_{\mathrm{PH}}\left(M-1\right)/M\sim$18 μm[Reference Sinars, Gregorian, Hammer and Maron16]. The field of view of the XRBL diagnostic for a single shock target together with an example of results is shown in Figures 2(d) and 2(e). It should be noted that for the shock speed of ![]() $\sim 40$ km/s, the motion blurring for a 1 ns exposure XRBL is
$\sim 40$ km/s, the motion blurring for a 1 ns exposure XRBL is ![]() $\sim 40$ μm, about twice the size of the pinhole.
$\sim 40$ μm, about twice the size of the pinhole.
3 Results
Results from single and colliding radiative shock experiments are presented in Figures 3(a) and 3(b), respectively. Each image was obtained from a different shot with similar initial conditions for the laser drive and gas-fill pressure. Overall, the results showed good shot-to-shot reproducibility for the shock dynamics. Average laser-drive parameters in these experiments were an energy of ![]() ${E}_{\mathrm{laser}}=960\pm 53$ J and a pulse duration of
${E}_{\mathrm{laser}}=960\pm 53$ J and a pulse duration of ![]() ${t}_{\mathrm{laser}}=1039\pm 63$ ps. The spot size was estimated from the full-width at half-maximum of Gaussian fits from X-ray self-emission recorded with the time-integrated pinhole camera (Figure 2(c)), resulting in an oval spot with size
${t}_{\mathrm{laser}}=1039\pm 63$ ps. The spot size was estimated from the full-width at half-maximum of Gaussian fits from X-ray self-emission recorded with the time-integrated pinhole camera (Figure 2(c)), resulting in an oval spot with size ![]() ${\varphi}_{\mathrm{laser}}\approx (424\pm 11\,\, \mu\textrm{m})\times (324\pm 15$ μm) (width
${\varphi}_{\mathrm{laser}}\approx (424\pm 11\,\, \mu\textrm{m})\times (324\pm 15$ μm) (width ![]() $\times$ height) and, thus, an average laser intensity of
$\times$ height) and, thus, an average laser intensity of ![]() ${I}_{\mathrm{laser}}\sim 8.6\times 1{0}^{14}$ W/cm2. The laser intensity could be lower than this measured value due to the spot size images being time-integrated.
${I}_{\mathrm{laser}}\sim 8.6\times 1{0}^{14}$ W/cm2. The laser intensity could be lower than this measured value due to the spot size images being time-integrated.

Figure 3 XRBL results for (a) single and (b) colliding shocks. Artefacts from hard X-ray background (see Figure 2(e)) have been removed for visual purposes. For colliding shocks, the position is taken relative to the left-hand side piston and the vertical arrows mark the approximate position of the shock fronts in each frame. The arrows suggest that the shocks interpenetrate; however, in reality the experiments are in a collisional regime where no interpenetration occurs.
Dark spots in the images are due to debris reaching the image plate, which appears to be more pronounced in the case of colliding shocks. The XRBL results were characterized by vertical bands with abrupt changes in X-ray intensity that are attributed to background X-ray emission coming from the laser–piston interaction (see the right-hand side of Figure 2(e)). These artefacts were removed from the images in Figure 3 by subtracting the average intensity distribution from regions where the shock was not present. Future experiments will look at reducing debris and background emission on the image plate by adding extra shielding on the targets.
Figure 3(a) shows the results for a single shock for times between 20 and 100 ns, with each image corresponding to a separate experiment with nominally identical initial conditions. The shocks show a semi-hemispherical shape with a good degree of axial symmetry (i.e., with respect to a height of 0 mm in the window). In the earliest image, at 20 ns, the shock front is seen as a fairly smooth feature; however, from 40 ns onwards the shock develops spatial nonuniformities that grow in size as time increases. Rough wavelengths of these features are ![]() $\lambda \sim 250$ μm at 80 ns and
$\lambda \sim 250$ μm at 80 ns and ![]() $\lambda \sim 500$ μm at 100 ns.
$\lambda \sim 500$ μm at 100 ns.
Figure 3(b) shows the results for two colliding shocks in a counter-propagating configuration. Before and after the collision, the two shocks show a good degree of left–right symmetry and thus demonstrate a well-controlled laser drive and a consistent target fabrication procedure. These results show similar dynamics to previous experiments on the Orion laser using xenon at the same initial gas mass density (![]() ${\rho}_{\mathrm{Xe}}\sim$ 1.6 mg/cm3)[8], thus proving that it is possible to carry on and improve similar experiments of this type using SG-II in the future.
${\rho}_{\mathrm{Xe}}\sim$ 1.6 mg/cm3)[8], thus proving that it is possible to carry on and improve similar experiments of this type using SG-II in the future.
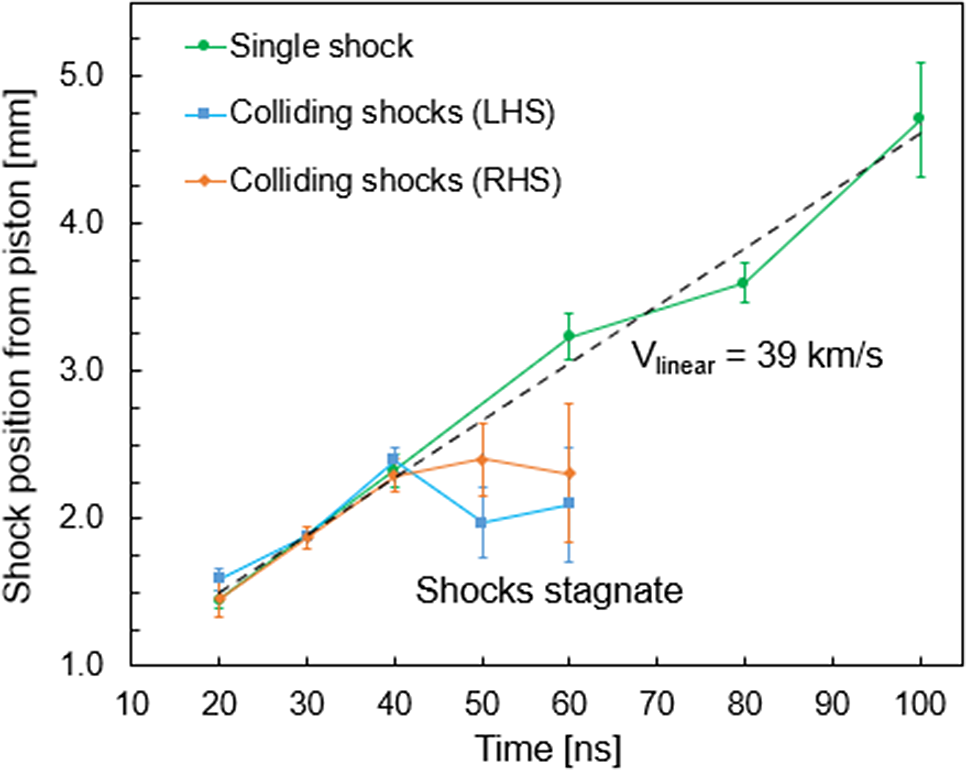
Figure 4 shows the position of the tip of the shock fronts with respect to the initial position of the piston for single and colliding shocks, measured from the data shown in Figure 3. For visual purposes, the position of the shocks is marked at 40, 50 and 60 ns, as if the shocks interpenetrated; however, the argon plasma in the shocks is expected to be in the collisional regime as the ion mean free path of argon is ![]() ${\lambda}_{\mathrm{mfp}}\lesssim 1$ μm[Reference Park, Ryutov, Ross, Kugland, Glenzer, Plechaty, Pollaine, Remington, Spitkovsky, Gargate, Gregori, Bell, Murphy, Sakawa, Kuramitsu, Morita, Takabe, Froula, Fiksel, Miniati, Koenig, Ravasio, Pelka, Liang, Woolsey, Kuranz, Drake and Grosskopf17]. This is estimated from plasma parameters from initial simulations presented later in the paper, together with an estimate of the average ionization of argon for these parameters from Ref. [Reference Espinosa, dríguez, Gil, Suzuki-Vidal, Lebedev, Ciardi, Rubiano and Martel18]. Figure 4 shows that the shock front position is fairly indistinguishable between single and colliding shocks up until 40 ns, that is, right at the time of the collision. The collision leads to the stagnation of the shocks, which is supported by the ram pressure of the piston material behind the shock front. For a single shock, a linear fit of the shock position as a function of time results in a velocity of
${\lambda}_{\mathrm{mfp}}\lesssim 1$ μm[Reference Park, Ryutov, Ross, Kugland, Glenzer, Plechaty, Pollaine, Remington, Spitkovsky, Gargate, Gregori, Bell, Murphy, Sakawa, Kuramitsu, Morita, Takabe, Froula, Fiksel, Miniati, Koenig, Ravasio, Pelka, Liang, Woolsey, Kuranz, Drake and Grosskopf17]. This is estimated from plasma parameters from initial simulations presented later in the paper, together with an estimate of the average ionization of argon for these parameters from Ref. [Reference Espinosa, dríguez, Gil, Suzuki-Vidal, Lebedev, Ciardi, Rubiano and Martel18]. Figure 4 shows that the shock front position is fairly indistinguishable between single and colliding shocks up until 40 ns, that is, right at the time of the collision. The collision leads to the stagnation of the shocks, which is supported by the ram pressure of the piston material behind the shock front. For a single shock, a linear fit of the shock position as a function of time results in a velocity of ![]() ${V}_{\mathrm{shock}\kern0.17em \mathrm{front}}\sim 39$ km/s.
${V}_{\mathrm{shock}\kern0.17em \mathrm{front}}\sim 39$ km/s.
To complement the experimental results, preliminary numerical simulations of the experiments are presented in Figure 3 for a single shock at 20 ns. The simulations were performed with the 2D radiative hydrodynamics code ARWEN[Reference Ogando, Velarde and Quant19, Reference García-Senz, Velarde, Suzuki-Vidal, Stehlé, Cotelo, Portillo, Plewa and Pak20]. A full comparison with the experimental data requires further testing of these simulations with several initial conditions; thus, this single output is used to infer characteristic plasma conditions and make first estimates, and further work will look at presenting a detailed simulation study. These first simulations were obtained using the initial conditions in the experiments, that is, an initial argon pressure of ![]() ${P}_0=1$ bar (
${P}_0=1$ bar (![]() ${\rho}_0=1.67$ mg/cm3), a laser-drive energy of
${\rho}_0=1.67$ mg/cm3), a laser-drive energy of ![]() ${E}_{\mathrm{laser}}=962$ J, a duration of
${E}_{\mathrm{laser}}=962$ J, a duration of ![]() ${t}_{\mathrm{laser}}=1$ ns and a focal spot of diameter
${t}_{\mathrm{laser}}=1$ ns and a focal spot of diameter ![]() ${\varphi}_{\mathrm{laser}}=370$ μm. The resolution of the simulations was 7 μm.
${\varphi}_{\mathrm{laser}}=370$ μm. The resolution of the simulations was 7 μm.
Figure 5 shows 2D maps of mass density and temperature together with axial (at a radius of r = 0 mm) lineouts of these quantities and materials and ionization. The profiles of density, temperature and ionization are representative of the typical structure of a radiative shock: a sharp jump in temperature and density at the shock front position (shown as a vertical dashed line at ![]() $\sim 1.79$ mm), followed by a decrease in temperature and an increase in density post-shock, which we identify as the cooling region. The post-shock region extends for
$\sim 1.79$ mm), followed by a decrease in temperature and an increase in density post-shock, which we identify as the cooling region. The post-shock region extends for ![]() $\sim 20$ μm with a characteristic mass density of
$\sim 20$ μm with a characteristic mass density of ![]() ${\rho}_{\mathrm{post}-\mathrm{shock}}\sim 12\hbox{--} 15$ mg/cm3 resulting in a density jump of
${\rho}_{\mathrm{post}-\mathrm{shock}}\sim 12\hbox{--} 15$ mg/cm3 resulting in a density jump of ![]() ${\rho}_{\mathrm{post}-\mathrm{shock}}/{\rho}_0\sim 12/1.67\sim 7$, of the order of the density jump of four expected for a strong shock. The profile of materials post-shock shows a mixing region of CH–Br and Ar extending up to
${\rho}_{\mathrm{post}-\mathrm{shock}}/{\rho}_0\sim 12/1.67\sim 7$, of the order of the density jump of four expected for a strong shock. The profile of materials post-shock shows a mixing region of CH–Br and Ar extending up to ![]() $\sim 1.77$ mm. The temperature in the shock peaks at
$\sim 1.77$ mm. The temperature in the shock peaks at ![]() $T\sim 20$ eV, and the temperature profile is characterized by a pre-heating region ahead of the shock with T
$T\sim 20$ eV, and the temperature profile is characterized by a pre-heating region ahead of the shock with T ![]() $\sim$ 2–5 eV, which can be identified as the radiative precursor.
$\sim$ 2–5 eV, which can be identified as the radiative precursor.

Figure 5 Numerical simulations of the experiments with the 2D radiation hydrodynamics code ARWEN at 20 ns. (a) Maps of mass density and temperature. (b) Axial lineouts (at a radius of 0 mm) of mass density, temperature, materials and ionization from (a).
4 Discussion and conclusions
We have presented the first results from experiments looking at the formation of radiative shocks in argon with piston-driven gas cells on the SG-II laser. The main diagnostic fielded was point-projection XRBL which, combined with a new gas-cell design, allowed the study of shock evolution for single and counter-propagating colliding shocks. In the case of colliding shocks, the results are similar to previous experiments using the Orion laser, demonstrating the feasibility of this platform on SG-II to carry out future experiments of this type. The study of the post-shock region in single shocks had not been looked at in detail in previous experiments (e.g., on Orion and other similar laser facilities). For instance, work in Ref. [5] and references therein have mostly focused on the radiative precursor region ahead of the shock and rarely studied the dense post-shock region.
One of the main results of these experiments on SG-II was to study the morphology of a single shock up to 100 ns to understand its evolution. The shock is characterized by the growth of spatial nonuniformities, with typical wavelengths ![]() $\lambda \sim 250\hbox{--} 500$ μm. Our first numerical simulations with the code ARWEN show the formation of similar features at 20 ns with a rough wavelength of
$\lambda \sim 250\hbox{--} 500$ μm. Our first numerical simulations with the code ARWEN show the formation of similar features at 20 ns with a rough wavelength of ![]() $\lambda \sim 125$ μm, in line with the experimental results; however, it is not clear how sensitive these features are to different initial conditions in the simulations and how these features can change if the resolution of the XRBL diagnostic is improved.
$\lambda \sim 125$ μm, in line with the experimental results; however, it is not clear how sensitive these features are to different initial conditions in the simulations and how these features can change if the resolution of the XRBL diagnostic is improved.
We can estimate characteristic time scales for the growth of hydrodynamic instabilities from a shocked-clump model presented in Ref. [Reference Hansen, Frank, Hartigan and Lebedev21]. For a strong shock, the Rayleigh–Taylor instability is expected to grow in a time scale given by  ${t}_{\mathrm{RT}}\sim \frac{\sqrt{\eta}\;{r}_{\mathrm{spot}}}{v_{\mathrm{shock}}}$ with
${t}_{\mathrm{RT}}\sim \frac{\sqrt{\eta}\;{r}_{\mathrm{spot}}}{v_{\mathrm{shock}}}$ with ![]() $\eta$ the ratio of post-shock to pre-shock density,
$\eta$ the ratio of post-shock to pre-shock density, ![]() ${r}_{\mathrm{spot}}$ the radius of the laser focal spot and
${r}_{\mathrm{spot}}$ the radius of the laser focal spot and ![]() ${v}_{\mathrm{shock}}$ the tip shock velocity. From the simulations at 20 ns we estimate
${v}_{\mathrm{shock}}$ the tip shock velocity. From the simulations at 20 ns we estimate ![]() $\eta \sim 12/1.67\sim 7$ and from the experiments
$\eta \sim 12/1.67\sim 7$ and from the experiments ![]() ${r}_{\mathrm{spot}}\sim 185$ μm and
${r}_{\mathrm{spot}}\sim 185$ μm and ![]() ${v}_{\mathrm{shock}}\sim 39$ km/s, resulting in
${v}_{\mathrm{shock}}\sim 39$ km/s, resulting in ![]() ${t}_{\mathrm{RT}}\sim 5$ ns, in line with the experimental results. Similarly, the growth of the non-linear thin shell instability (NLTSI) is given by the fragmentation time
${t}_{\mathrm{RT}}\sim 5$ ns, in line with the experimental results. Similarly, the growth of the non-linear thin shell instability (NLTSI) is given by the fragmentation time  ${t}_{\mathrm{frag}}\sim \frac{h}{C_{\mathrm{s}}}$, with
${t}_{\mathrm{frag}}\sim \frac{h}{C_{\mathrm{s}}}$, with ![]() $h$ the thickness of the shocked layer and
$h$ the thickness of the shocked layer and ![]() ${C}_{\mathrm{s}}$ its sound speed. For shocked argon at a temperature of
${C}_{\mathrm{s}}$ its sound speed. For shocked argon at a temperature of ![]() $T\sim 20$ eV,
$T\sim 20$ eV, ![]() ${C}_{\mathrm{s}}\sim 9$ km/s, and for a shock thickness of
${C}_{\mathrm{s}}\sim 9$ km/s, and for a shock thickness of ![]() $h\sim 100$ μm this results in
$h\sim 100$ μm this results in ![]() ${t}_{\mathrm{frag}}\sim 10$ ns, again consistent with the time scales observed in the experiments presented here.
${t}_{\mathrm{frag}}\sim 10$ ns, again consistent with the time scales observed in the experiments presented here.
The role of radiative cooling in the shock can be estimated using the plasma parameters from the simulations of ![]() $\rho \sim 10$ mg/cm3 and
$\rho \sim 10$ mg/cm3 and ![]() $T\sim 20$ eV. The expected cooling time for argon for these conditions (see Figure 4 in Ref. [Reference Espinosa, dríguez, Gil, Suzuki-Vidal, Lebedev, Ciardi, Rubiano and Martel18]) is
$T\sim 20$ eV. The expected cooling time for argon for these conditions (see Figure 4 in Ref. [Reference Espinosa, dríguez, Gil, Suzuki-Vidal, Lebedev, Ciardi, Rubiano and Martel18]) is ![]() ${t}_{\mathrm{cool}}\sim 1$ ns, indicating that the plasma in the shock is radiatively cooled and thus could be prone to the formation of instabilities mediated by radiative losses. We note that the formation of similar spatial features was also observed in previous laser experiments with shocks in argon[Reference Loupias, Gregory, Falize, Waugh, Seiichi, Pikuz, Kuramitsu, Ravasio, Bouquet, Michaut, Barroso, Rabec le Gloahec, Nazarov, Takabe, Sakawa, Woolsey and Koenig22], pointing to a common cause. It is worth noting the work in Refs. [Reference Visco, Drake, Glenzer, Döppner, Gregori, Froula and Grosskopf23,Reference Reighard, Drake, Donajkowski, Grosskopf, Dannenberg, Froula, Glenzer, Ross and Edwards24] driving shocks in argon at a pressure of 1 bar; however, besides these works, we were unable to find imaging results that provide data on the shock morphology.
${t}_{\mathrm{cool}}\sim 1$ ns, indicating that the plasma in the shock is radiatively cooled and thus could be prone to the formation of instabilities mediated by radiative losses. We note that the formation of similar spatial features was also observed in previous laser experiments with shocks in argon[Reference Loupias, Gregory, Falize, Waugh, Seiichi, Pikuz, Kuramitsu, Ravasio, Bouquet, Michaut, Barroso, Rabec le Gloahec, Nazarov, Takabe, Sakawa, Woolsey and Koenig22], pointing to a common cause. It is worth noting the work in Refs. [Reference Visco, Drake, Glenzer, Döppner, Gregori, Froula and Grosskopf23,Reference Reighard, Drake, Donajkowski, Grosskopf, Dannenberg, Froula, Glenzer, Ross and Edwards24] driving shocks in argon at a pressure of 1 bar; however, besides these works, we were unable to find imaging results that provide data on the shock morphology.
The use of argon at a relatively high initial pressure (1 bar) and the resulting shock velocity of ![]() $\sim 40$ km/s opens the question of the importance of radiative effects in these experiments. These effects can be quantified using the Boltzmann and Mihalas numbers following the definitions in Refs. [Reference Mabey, Michel, Albertazzi, Falize, Charpentier and Koenig3,Reference Chaulagain, Stehl, Larour, Kozlov, Suzuki-Vidal, Barroso, Cotelo, Velarde, Rodriguez, Gil, Ciardi, Acef, Nejdl, de S, Singh, Ibgui and Champion12,Reference Falize, Michaut and Bouquet25], and references therein. For the plasma conditions from our first simulations we estimate a Boltzmann number
$\sim 40$ km/s opens the question of the importance of radiative effects in these experiments. These effects can be quantified using the Boltzmann and Mihalas numbers following the definitions in Refs. [Reference Mabey, Michel, Albertazzi, Falize, Charpentier and Koenig3,Reference Chaulagain, Stehl, Larour, Kozlov, Suzuki-Vidal, Barroso, Cotelo, Velarde, Rodriguez, Gil, Ciardi, Acef, Nejdl, de S, Singh, Ibgui and Champion12,Reference Falize, Michaut and Bouquet25], and references therein. For the plasma conditions from our first simulations we estimate a Boltzmann number ![]() $\sim 1$ and a Mihalas number of
$\sim 1$ and a Mihalas number of ![]() $\sim 1{0}^3$. The latter is unsurprising as only a handful of experiments in the past have claimed to be in a pressure-dominated regime (see e.g., Ref. [Reference Dizière, Michaut, Koenig, Gregory, Ravasio, Sakawa, Kuramitsu, Morita, Ide, Tanji, Takabe, Barroso and Boudenne26]). A Boltzmann number
$\sim 1{0}^3$. The latter is unsurprising as only a handful of experiments in the past have claimed to be in a pressure-dominated regime (see e.g., Ref. [Reference Dizière, Michaut, Koenig, Gregory, Ravasio, Sakawa, Kuramitsu, Morita, Ide, Tanji, Takabe, Barroso and Boudenne26]). A Boltzmann number ![]() $\sim 1$ implies that the radiative flow in our experiments is of the same order as the material flow, which means we are in the threshold where the shock might not be strongly influenced by radiation. Looking at radiative effects from intermediate cases like this one to the case where the structure is dominated by radiation is necessary for a better understanding of the radiation of effect on shock waves as a general topic, which remains a very difficult topic at present.
$\sim 1$ implies that the radiative flow in our experiments is of the same order as the material flow, which means we are in the threshold where the shock might not be strongly influenced by radiation. Looking at radiative effects from intermediate cases like this one to the case where the structure is dominated by radiation is necessary for a better understanding of the radiation of effect on shock waves as a general topic, which remains a very difficult topic at present.
Future work on SG-II will aim at providing more statistics of single shocks in argon and assess the role of radiative losses in the formation of these features. This will be complemented by a more detailed simulation work with the ARWEN code.
Acknowledgements
This research was supported by the Royal Society (UK) through a University Research Fellowship (URF-R-180032), a Research Fellows Enhancement Award (RGF-EA-180240), an International Exchanges grant (IES-R3-170140), and a Research Grant (RG2017-R2). The authors would like to thank the operation group of the SG-II laser facility. C.S. acknowledges support from the French INSU-PNPS programme. U.C. acknowledges support by the project Advanced Research (CZ.02.1.01/0.0/0.0/16_019/0000789) from European Regional Development Fund (ADONIS). F.S.-V. acknowledges technical support from Paul Brown, Alan Finch and the entire team at the Physics Mechanical Instrumentation Workshop at Imperial College London.