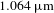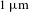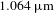1 Introduction
In the context of the continuously increasing average power of high-energy class diode pumped solid-state lasers (HEC-DPSSLs), careful treatment of the thermal effects due to the parasitic absorption of power in optical components has become tremendously important for the further development of HEC-DPSSLs[Reference Mason, Divoky, Ertel, Pilar, Butcher, Hanus, Banerjee, Phillips, Smith, Vido, Lucianetti, Hernandez-Gomez, Edwards, Mocek and Collier1–Reference Novak, Miura, Smrz, Chyla, Nagisetty, Muzik, Linnemann, Turcicova, Jambunathan, Slezak, Sawicka-Chyla, Pilar, Bonora, Divoky, Mesicek, Pranovich, Sikocinski, Huynh, Severova, Navratil, Vojna, Horackova, Mann, Lucianetti, Endo, Rostohar and Mocek4]. One of the most seriously affected optical components is the Faraday isolator (FI), because of the relatively high absorption (
![]() ${\sim}10^{-3}~\text{cm}^{-1}$
) of the currently available magneto-optical elements (MOEs).
${\sim}10^{-3}~\text{cm}^{-1}$
) of the currently available magneto-optical elements (MOEs).
When an MOE is exposed to high-average-power laser radiation, a nonuniform temperature distribution is generated over the MOE cross-section as a result of absorption. This nonuniformity in temperature results in a nonuniform distribution of the polarization plane rotation angle due to the temperature dependence of the Verdet constant, as well as the thermally induced birefringence (the photoelastic effect). As a consequence, the polarization state of the transmitted radiation is rotated undesirably, deteriorating the isolation ratio of the FI[Reference Khazanov5]. Furthermore, the absorption-induced nonuniform temperature distribution also leads to the thermal lensing phenomena causing wavefront aberrations of the passing laser beam[Reference Khazanov, Andreev, Malshakov, Palashov, Poteomkin, Sergeev, Shaykin, Zelenogorsky, Ivanov, Amin, Mueller, Tanner and Reitze6].
There are several ways to suppress the degrading effect of polarization and modal distortion incorporating, for example, a special magnetic field design[Reference Mironov, Voitovich, Starobor and Palashov7], thermo-mechanical designing of an MOE holder[Reference Mironov, Voitovich and Palashov8], cryogenic cooling[Reference Zheleznov, Zelenogorskii, Katin, Mukhin, Palashov and Khazanov9, Reference Zheleznov, Starobor, Palashov and Khazanov10], or designing of a heat removal scheme using numerical modeling[Reference Snetkov, Mukhin, Palashov and Khazanov11–Reference Vojna, Slezak, Lucianetti and Mocek13].
A great number of recent publications also focus on the investigation of new magneto-optical materials with high Verdet constant, high transparency, and excellent thermal properties, to enable reduction of the heat generated in an MOE. For shorter laser wavelengths (
![]() ${<}0.5~\unicode[STIX]{x03BC}\text{m}$
), fluorides, such as CeF3 or PrF3, are the best candidates for an FI, since they exhibit superior magneto-optical characteristics in this spectral range[Reference Vasyliev, Villora, Nakamura, Sugahara and Shimamura14, Reference Vojna, Yasuhara, Slezak, Muzik, Lucianetti and Mocek15]. For the visible (VIS) and near-infrared (NIR) laser wavelengths, terbium gallium garnet (TGG) represents the most commonly used magneto-optical material[Reference Slezak, Yasuhara, Lucianetti and Mocek16–Reference Yasuhara, Tokita, Kawanaka, Kawashima, Kan, Yagi, Nozawa, Yanagitani, Fujimoto, Yoshida and Nakatsuka18]. Recently, there has been an increasing trend in investigating new materials which could supersede TGG, as it is limited by increasing absorption losses, and large-aperture TGG elements are difficult to manufacture[Reference Villora, Molina, Nakamura, Shimamura, Hatanaka, Funaki and Naoe19]. In this manner, a terbium scandium aluminum garnet (TSAG) crystal[Reference Snetkov, Yasuhara, Starobor, Mironov and Palashov20], terbium aluminum garnet (TAG) ceramics[Reference Zheleznov, Starobor, Palashov, Chen and Zhou21], cerium-doped TAG ceramics[Reference Zheleznov, Starobor, Palashov, Lin and Zhou22], or rare-earth (RE) elements-doped TGG crystals[Reference Chen, Yang, Wang and Yin23, Reference Chen, Yang, Wang and Yin24] were reported as potential material candidates for the future generation of VIS–NIR FIs. Most recently, attention was also brought toward RE sesquioxides (RE2O3) containing a very high concentration of RE3+ ions, which are highly magnetically active. Magneto-optical characteristics of Tb2O3
[Reference Snetkov, Permin, Balabanov and Palashov25], Dy2O3
[Reference Morales, Amos, Khizroev and Garay26] and Ho2O3
[Reference Furuse and Yasuhara27] were reported to predict a huge potential in these materials. For instance, Tb2O3 possesses a Verdet constant that is approximately three times higher than the Verdet constant of TGG at
${<}0.5~\unicode[STIX]{x03BC}\text{m}$
), fluorides, such as CeF3 or PrF3, are the best candidates for an FI, since they exhibit superior magneto-optical characteristics in this spectral range[Reference Vasyliev, Villora, Nakamura, Sugahara and Shimamura14, Reference Vojna, Yasuhara, Slezak, Muzik, Lucianetti and Mocek15]. For the visible (VIS) and near-infrared (NIR) laser wavelengths, terbium gallium garnet (TGG) represents the most commonly used magneto-optical material[Reference Slezak, Yasuhara, Lucianetti and Mocek16–Reference Yasuhara, Tokita, Kawanaka, Kawashima, Kan, Yagi, Nozawa, Yanagitani, Fujimoto, Yoshida and Nakatsuka18]. Recently, there has been an increasing trend in investigating new materials which could supersede TGG, as it is limited by increasing absorption losses, and large-aperture TGG elements are difficult to manufacture[Reference Villora, Molina, Nakamura, Shimamura, Hatanaka, Funaki and Naoe19]. In this manner, a terbium scandium aluminum garnet (TSAG) crystal[Reference Snetkov, Yasuhara, Starobor, Mironov and Palashov20], terbium aluminum garnet (TAG) ceramics[Reference Zheleznov, Starobor, Palashov, Chen and Zhou21], cerium-doped TAG ceramics[Reference Zheleznov, Starobor, Palashov, Lin and Zhou22], or rare-earth (RE) elements-doped TGG crystals[Reference Chen, Yang, Wang and Yin23, Reference Chen, Yang, Wang and Yin24] were reported as potential material candidates for the future generation of VIS–NIR FIs. Most recently, attention was also brought toward RE sesquioxides (RE2O3) containing a very high concentration of RE3+ ions, which are highly magnetically active. Magneto-optical characteristics of Tb2O3
[Reference Snetkov, Permin, Balabanov and Palashov25], Dy2O3
[Reference Morales, Amos, Khizroev and Garay26] and Ho2O3
[Reference Furuse and Yasuhara27] were reported to predict a huge potential in these materials. For instance, Tb2O3 possesses a Verdet constant that is approximately three times higher than the Verdet constant of TGG at
![]() $1.064~\unicode[STIX]{x03BC}\text{m}$
. The Verdet constant of Dy2O3 approximately doubles that of TGG at
$1.064~\unicode[STIX]{x03BC}\text{m}$
. The Verdet constant of Dy2O3 approximately doubles that of TGG at
![]() $0.633~\unicode[STIX]{x03BC}\text{m}$
, but it exhibits strong absorption in the desired spectral range for HEC-DPSSLs around
$0.633~\unicode[STIX]{x03BC}\text{m}$
, but it exhibits strong absorption in the desired spectral range for HEC-DPSSLs around
![]() $1~\unicode[STIX]{x03BC}\text{m}$
. On the other hand, Ho2O3 has no dominant absorption between 1–
$1~\unicode[STIX]{x03BC}\text{m}$
. On the other hand, Ho2O3 has no dominant absorption between 1–
![]() $1.1~\unicode[STIX]{x03BC}\text{m}$
and possesses a Verdet constant comparable to TAG ceramics (
$1.1~\unicode[STIX]{x03BC}\text{m}$
and possesses a Verdet constant comparable to TAG ceramics (
![]() ${\sim}1.3$
higher than TGG at
${\sim}1.3$
higher than TGG at
![]() $1.064~\unicode[STIX]{x03BC}\text{m}$
).
$1.064~\unicode[STIX]{x03BC}\text{m}$
).
In this work we report measurements of the Faraday effect in Ho2O3 ceramics-based magneto-optical materials, advancing the analysis from the previous work[Reference Furuse and Yasuhara27]. Section 2 is dedicated to a laser measurement of the Verdet constant temperature dependence of Ho2O3 ceramics at
![]() $1.064~\unicode[STIX]{x03BC}\text{m}$
, which was, to the best of our knowledge, yet-unknown. Knowledge of the temperature dependence of the Verdet constant is valuable for the design of more advanced compensation schemes for the suppression of thermal effects in FIs, which were mentioned earlier in the introduction. In Section 3 of this paper, we present experimental results obtained for the Verdet constant dispersion of Ho2O3 ceramics samples doped with Tb3+ or Ce3+ ions, which may possibly boost the Faraday rotation effect of the host material. Conclusions are drawn based on the experimental findings in Section 4 of this paper.
$1.064~\unicode[STIX]{x03BC}\text{m}$
, which was, to the best of our knowledge, yet-unknown. Knowledge of the temperature dependence of the Verdet constant is valuable for the design of more advanced compensation schemes for the suppression of thermal effects in FIs, which were mentioned earlier in the introduction. In Section 3 of this paper, we present experimental results obtained for the Verdet constant dispersion of Ho2O3 ceramics samples doped with Tb3+ or Ce3+ ions, which may possibly boost the Faraday rotation effect of the host material. Conclusions are drawn based on the experimental findings in Section 4 of this paper.

Figure 1. Simplified scheme of the experimental setup for laser measurement of the Verdet constant temperature dependence.
2 Laser measurement of the Verdet constant temperature dependence of Ho2O3
A simplified scheme of the experimental setup used for the laser measurement of the Verdet constant temperature dependence is depicted in Figure 1. During the experiment a laser probe beam (
![]() $\unicode[STIX]{x1D706}=1.064~\unicode[STIX]{x03BC}\text{m}$
) was linearly polarized by an input Glan polarizer and propagated through a measured material sample, which was placed inside a cryostat enabling temperature control. An external magnetic field was applied on the sample, inducing Faraday rotation of the propagating probe beam. With the polarization plane rotated, the beam exited the sample and was further processed by a detection system. The detection system consisted of an output Glan polarizer (the analyzer), which can be arbitrarily rotated around the optical axis, and a power meter.
$\unicode[STIX]{x1D706}=1.064~\unicode[STIX]{x03BC}\text{m}$
) was linearly polarized by an input Glan polarizer and propagated through a measured material sample, which was placed inside a cryostat enabling temperature control. An external magnetic field was applied on the sample, inducing Faraday rotation of the propagating probe beam. With the polarization plane rotated, the beam exited the sample and was further processed by a detection system. The detection system consisted of an output Glan polarizer (the analyzer), which can be arbitrarily rotated around the optical axis, and a power meter.

Figure 2. An example of measured data gathered for one temperature step (at 300 K).
The corresponding transmitted laser power was detected in a large number (a few hundreds) of analyzer angular positions with a
![]() $0.1^{\circ }$
angular step. The measurement was performed for several temperatures ranging from 305 down to 15 K. For each temperature
$0.1^{\circ }$
angular step. The measurement was performed for several temperatures ranging from 305 down to 15 K. For each temperature
![]() $T_{i}$
, the measurement was taken twice, with and without an external magnetic field applied. An example of measured data gathered for one temperature step is depicted in Figure 2. According to the Malus law, the power data gathered in each individual measurement was fitted with the following cosine squared function
$T_{i}$
, the measurement was taken twice, with and without an external magnetic field applied. An example of measured data gathered for one temperature step is depicted in Figure 2. According to the Malus law, the power data gathered in each individual measurement was fitted with the following cosine squared function
where
![]() $\unicode[STIX]{x1D6FC}$
denotes the analyzer angular position,
$\unicode[STIX]{x1D6FC}$
denotes the analyzer angular position,
![]() $T_{i}$
is the temperature,
$T_{i}$
is the temperature,
![]() $P(\unicode[STIX]{x1D6FC},T_{i})$
refers to the recorded power data, and
$P(\unicode[STIX]{x1D6FC},T_{i})$
refers to the recorded power data, and
![]() $A_{1-3}(T_{i})$
are the fitting parameters. The polarization plane rotation angle
$A_{1-3}(T_{i})$
are the fitting parameters. The polarization plane rotation angle
![]() $\unicode[STIX]{x1D703}(T_{i})$
was directly calculated as a difference between the initial phase shifts
$\unicode[STIX]{x1D703}(T_{i})$
was directly calculated as a difference between the initial phase shifts
![]() $\unicode[STIX]{x1D703}(T_{i})=A_{2N}(T_{i})-A_{2B}(T_{i})$
obtained for the cases with the magnetic field –
$\unicode[STIX]{x1D703}(T_{i})=A_{2N}(T_{i})-A_{2B}(T_{i})$
obtained for the cases with the magnetic field –
![]() $A_{2B}(T_{i})$
– and without it –
$A_{2B}(T_{i})$
– and without it –
![]() $A_{2N}(T_{i})$
.
$A_{2N}(T_{i})$
.
The Verdet constant
![]() $V(T_{i})$
was obtained from the rotational angle
$V(T_{i})$
was obtained from the rotational angle
![]() $\unicode[STIX]{x1D703}(T_{i})$
using the following expression
$\unicode[STIX]{x1D703}(T_{i})$
using the following expression
in which
![]() $B(l)$
refers to the known longitudinal distribution of applied magnetic field[Reference Slezak, Yasuhara, Lucianetti and Mocek17] and
$B(l)$
refers to the known longitudinal distribution of applied magnetic field[Reference Slezak, Yasuhara, Lucianetti and Mocek17] and
![]() $L$
is the sample length.
$L$
is the sample length.
![]() $B_{\text{eff}}$
denotes the effective magnetic field magnitude which was obtained from the distribution by numeric integration over the length of the sample. Although an effort was made to place the sample exactly in the maximum of
$B_{\text{eff}}$
denotes the effective magnetic field magnitude which was obtained from the distribution by numeric integration over the length of the sample. Although an effort was made to place the sample exactly in the maximum of
![]() $B(l)$
of the permanent magnet, an uncertainty of
$B(l)$
of the permanent magnet, an uncertainty of
![]() $B_{\text{eff}}$
, given by the magnetic field measurement error as well as by an unintended misplacement of the sample, needs to be considered. The respective values derived for the uncertainty are listed in Table 1. The experimental data obtained for Verdet constant temperature dependence was further fitted with a simplified model function[Reference Slezak, Yasuhara, Lucianetti and Mocek17]
$B_{\text{eff}}$
, given by the magnetic field measurement error as well as by an unintended misplacement of the sample, needs to be considered. The respective values derived for the uncertainty are listed in Table 1. The experimental data obtained for Verdet constant temperature dependence was further fitted with a simplified model function[Reference Slezak, Yasuhara, Lucianetti and Mocek17]
where
![]() $G$
,
$G$
,
![]() $H$
and
$H$
and
![]() $T_{c}$
represent fitting parameters.
$T_{c}$
represent fitting parameters.
Table 1. Material parameters and the fitted parameters.

Apart from Ho2O3 ceramics sample, a TGG ceramic sample from Konoshima Chemical, Co., Ltd. was also measured using the above described experimental method. TGG ceramics represent a valid comparative reference of our measurement since it is nowadays the most widely used magneto-optical material for wavelengths around
![]() $1~\unicode[STIX]{x03BC}\text{m}$
. The experimental results obtained for both samples (Ho2O3 and TGG) are depicted in Figure 3, along with the fitting curves and other comparative measurements. The material parameters and the obtained fitting parameters are listed in Table 1. The relative error of the measurement was 4.17% for the Ho2O3 ceramics sample, and 4.18% for the TGG ceramics sample, only weakly changing across the whole measured temperature range.
$1~\unicode[STIX]{x03BC}\text{m}$
. The experimental results obtained for both samples (Ho2O3 and TGG) are depicted in Figure 3, along with the fitting curves and other comparative measurements. The material parameters and the obtained fitting parameters are listed in Table 1. The relative error of the measurement was 4.17% for the Ho2O3 ceramics sample, and 4.18% for the TGG ceramics sample, only weakly changing across the whole measured temperature range.

Figure 3. Experimental results for laser measurement of the Verdet constant temperature dependence of Ho2O3 ceramics.
Our experimental results obtained for the TGG sample are in good agreement with the previously reported measurements[Reference Yasuhara, Tokita, Kawanaka, Kawashima, Kan, Yagi, Nozawa, Yanagitani, Fujimoto, Yoshida and Nakatsuka18], as well as with our own unpublished laser measurements of the same TGG ceramics sample. The only exception in agreement can be observed at the lowest temperatures. However, it should be noted that in Ref. [Reference Yasuhara, Tokita, Kawanaka, Kawashima, Kan, Yagi, Nozawa, Yanagitani, Fujimoto, Yoshida and Nakatsuka18] the laser wavelength was
![]() $1.053~\unicode[STIX]{x03BC}\text{m}$
, and this difference can account for the slight discrepancy in the Verdet constant at the lowest temperatures. The other possible cause of the disagreement between the new and the unpublished measurements can be accounted to a larger value of
$1.053~\unicode[STIX]{x03BC}\text{m}$
, and this difference can account for the slight discrepancy in the Verdet constant at the lowest temperatures. The other possible cause of the disagreement between the new and the unpublished measurements can be accounted to a larger value of
![]() $\text{d}V/\text{d}T$
at lower temperatures, causing a larger absolute error of the Verdet constant, as a consequence of temperature fluctuations during the measurement. A slightly different mutual position of the sample and the magnet between the compared measurements also greatly contributes to the discrepancy at low temperatures. However, this issue may be overcome in the future via more mechanically sophisticated magnet alignment, which is currently under investigation.
$\text{d}V/\text{d}T$
at lower temperatures, causing a larger absolute error of the Verdet constant, as a consequence of temperature fluctuations during the measurement. A slightly different mutual position of the sample and the magnet between the compared measurements also greatly contributes to the discrepancy at low temperatures. However, this issue may be overcome in the future via more mechanically sophisticated magnet alignment, which is currently under investigation.
The Verdet constant temperature dependence of Ho2O3 at
![]() $1.064~\unicode[STIX]{x03BC}\text{m}$
is yet unknown and therefore no comparison can be made. Nevertheless, considering the good agreement of the TGG results, the presented results for Ho2O3 seem to be valid.
$1.064~\unicode[STIX]{x03BC}\text{m}$
is yet unknown and therefore no comparison can be made. Nevertheless, considering the good agreement of the TGG results, the presented results for Ho2O3 seem to be valid.
3 Verdet constant dispersion of Ho2O3 ceramics-based magneto-optical materials
Recent publications in the field of magneto-optical materials research showed that doping of a magneto-optical material by RE elements can boost the Faraday rotation effect in the host material[Reference Zheleznov, Starobor, Palashov, Lin and Zhou22–Reference Chen, Yang, Wang and Yin24]. The Verdet constant dispersion of Ho2O3 doped with Tb3+ or Ce3+ ions was measured in order to investigate the impact of doping on the Faraday effect in Ho2O3.
A simplified scheme of the experimental setup used for measurement of the Verdet constant dispersion is depicted in Figure 4. The experimental setup, as well as the experimental procedure, was similar to the laser measurement of temperature dependence of the Verdet constant, described in Section 2. There were a few differences which will be briefly explained in the next paragraph. The full description of the Verdet constant dispersion measurement is given in Ref. [Reference Vojna, Yasuhara, Slezak, Muzik, Lucianetti and Mocek15].

Figure 4. Simplified scheme of the experimental setup used for measurement of the Verdet constant dispersion.
Instead of a laser, a broadband radiation source (NKT Photonics SuperK Compact) was used for the Verdet constant dispersion measurement. The samples under investigation were no longer kept in the cryostat, but fixed in a mechanical holder outside it. The detection system needed to be modified as well, now consisting of the rotating output Glan polarizer (the analyzer), a silver-coated diffusive reflector, an integration sphere, and a spectrometer. The diffusive reflector helped to suppress the polarization dependence of the fiber coupling, through which the captured signal was transmitted to spectrometer (Ocean Optics HR4000CG-UV-NIR). The effective spectral range of the measurement was 0.5–
![]() $1~\unicode[STIX]{x03BC}\text{m}$
. The transmitted intensity spectra were captured using a full-circle rotation of the analyzer, with a
$1~\unicode[STIX]{x03BC}\text{m}$
. The transmitted intensity spectra were captured using a full-circle rotation of the analyzer, with a
![]() $2^{\circ }$
angular step, giving a total number of 181 angular points for each wavelength detected with the spectrometer. The intensity data was, again, gathered for two distinctive cases – with and without an external magnetic field. The measured data for each wavelength
$2^{\circ }$
angular step, giving a total number of 181 angular points for each wavelength detected with the spectrometer. The intensity data was, again, gathered for two distinctive cases – with and without an external magnetic field. The measured data for each wavelength
![]() $\unicode[STIX]{x1D706}_{i}$
was fitted with the following cosine squared function
$\unicode[STIX]{x1D706}_{i}$
was fitted with the following cosine squared function
where
![]() $I_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706}_{i})$
denotes the measured intensity data normalized to unity,
$I_{n}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D706}_{i})$
denotes the measured intensity data normalized to unity,
![]() $\unicode[STIX]{x1D6FC}$
is the analyzer position, and
$\unicode[STIX]{x1D6FC}$
is the analyzer position, and
![]() $\unicode[STIX]{x1D6FC}_{0}(\unicode[STIX]{x1D706}_{i})$
represents the fitting parameter, the initial phase shift. The polarization plane rotation angle
$\unicode[STIX]{x1D6FC}_{0}(\unicode[STIX]{x1D706}_{i})$
represents the fitting parameter, the initial phase shift. The polarization plane rotation angle
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})$
was directly calculated as the difference between the initial phase shifts
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})$
was directly calculated as the difference between the initial phase shifts
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})=\unicode[STIX]{x1D6FC}_{0N}(\unicode[STIX]{x1D706}_{i})-\unicode[STIX]{x1D6FC}_{0B}(\unicode[STIX]{x1D706}_{i})$
obtained for the cases when the external magnetic field was applied -
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})=\unicode[STIX]{x1D6FC}_{0N}(\unicode[STIX]{x1D706}_{i})-\unicode[STIX]{x1D6FC}_{0B}(\unicode[STIX]{x1D706}_{i})$
obtained for the cases when the external magnetic field was applied -
![]() $\unicode[STIX]{x1D6FC}_{0B}(\unicode[STIX]{x1D706}_{i})$
- and when it was not -
$\unicode[STIX]{x1D6FC}_{0B}(\unicode[STIX]{x1D706}_{i})$
- and when it was not -
![]() $\unicode[STIX]{x1D6FC}_{0N}(\unicode[STIX]{x1D706}_{i})$
. The Verdet constant dispersion
$\unicode[STIX]{x1D6FC}_{0N}(\unicode[STIX]{x1D706}_{i})$
. The Verdet constant dispersion
![]() $V(\unicode[STIX]{x1D706}_{i})$
was obtained from the rotational angle
$V(\unicode[STIX]{x1D706}_{i})$
was obtained from the rotational angle
![]() $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})$
using an expression analog to the expression (2), namely
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})$
using an expression analog to the expression (2), namely
![]() $V(\unicode[STIX]{x1D706}_{i})=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})/(B_{\text{eff}}L)$
. The measurement was performed at room temperature.
$V(\unicode[STIX]{x1D706}_{i})=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D706}_{i})/(B_{\text{eff}}L)$
. The measurement was performed at room temperature.
Table 2. Material parameters for the samples under investigation for the Verdet constant dispersion measurement.


Figure 5. The experimental results obtained for the Verdet constant dispersion of Ho2O3 ceramics-based magneto-optical materials.
Specific parameters of the samples under investigation are listed in Table 2. The experimental results obtained for the Verdet constant dispersion
![]() $V(\unicode[STIX]{x1D706}_{i})$
are depicted in Figure 5. Figure 5 further contains values of the Verdet constant obtained by the laser measurement. The relative error of the measurement was around 4% in the whole spectral range of the measurement. At this point, it is worth to remark that the Ho2O3 material possesses several electronic transitions within the measured spectral range[Reference Furuse and Yasuhara27]. A proper model function appropriately describing the obtained Verdet constant dispersion is currently under investigation; therefore, only the raw data are presented in this paper, which, for the purposes of a preliminary doping impact investigation, is satisfactory. Examining the experimental results we may conclude that doping of Ho2O3 by RE elements has no significant impact on the Verdet constant. However, it needs to be taken into account that: (a) the doping level of the investigated samples was relatively low, (b) the investigated samples were relatively shorter, thereby inducing only a small Faraday rotation of the probe beam, and finally (c) the optical quality of the provided material samples was limited. The in-line transmittance of the material samples was not investigated within the scope of this work; however, as it was mentioned in the previous work[Reference Furuse and Yasuhara27], the in-line transmittance of the nondoped Ho2O3 ceramics sample at
$V(\unicode[STIX]{x1D706}_{i})$
are depicted in Figure 5. Figure 5 further contains values of the Verdet constant obtained by the laser measurement. The relative error of the measurement was around 4% in the whole spectral range of the measurement. At this point, it is worth to remark that the Ho2O3 material possesses several electronic transitions within the measured spectral range[Reference Furuse and Yasuhara27]. A proper model function appropriately describing the obtained Verdet constant dispersion is currently under investigation; therefore, only the raw data are presented in this paper, which, for the purposes of a preliminary doping impact investigation, is satisfactory. Examining the experimental results we may conclude that doping of Ho2O3 by RE elements has no significant impact on the Verdet constant. However, it needs to be taken into account that: (a) the doping level of the investigated samples was relatively low, (b) the investigated samples were relatively shorter, thereby inducing only a small Faraday rotation of the probe beam, and finally (c) the optical quality of the provided material samples was limited. The in-line transmittance of the material samples was not investigated within the scope of this work; however, as it was mentioned in the previous work[Reference Furuse and Yasuhara27], the in-line transmittance of the nondoped Ho2O3 ceramics sample at
![]() $1~\unicode[STIX]{x03BC}\text{m}$
wavelength is
$1~\unicode[STIX]{x03BC}\text{m}$
wavelength is
![]() ${\sim}60\%$
. The optical quality of the doped samples was comparable to the nondoped sample from the previous work.
${\sim}60\%$
. The optical quality of the doped samples was comparable to the nondoped sample from the previous work.
After a significant improvement of provided Ho2O3 samples’ optical quality, longer samples may be produced and then a more comprehensive characterization of RE elements-doped Ho2O3 samples can be made.
4 Conclusions
In this work, we report on Faraday effect measurements of Ho2O3 ceramics-based magneto-optical materials, potential MOE candidates for FIs for HEC-DPSSLs. The temperature dependence of the Verdet constant of nondoped Ho2O3 ceramics was presented for temperatures 15–305 K and at the wavelength of
![]() $1.064~\unicode[STIX]{x03BC}\text{m}$
for the first time. Experimental data for the Verdet constant dispersion at wavelengths 0.5–
$1.064~\unicode[STIX]{x03BC}\text{m}$
for the first time. Experimental data for the Verdet constant dispersion at wavelengths 0.5–
![]() $1~\unicode[STIX]{x03BC}\text{m}$
and
$1~\unicode[STIX]{x03BC}\text{m}$
and
![]() $1.064~\unicode[STIX]{x03BC}\text{m}$
, for both nondoped Ho2O3 and Ho2O3 doped with Tb3+ (0.2 at. %) and Ce3+ (0.1 at. %) ions, was presented with the conclusion that the relatively low level of doping has no significant boosting impact on the Faraday effect. More comprehensive investigations of dopants and their concentrations are needed in order to assess the benefit of doping of Ho2O3 with RE ions. Improvement of the optical quality is also essential for a future material utilization as an MOE.
$1.064~\unicode[STIX]{x03BC}\text{m}$
, for both nondoped Ho2O3 and Ho2O3 doped with Tb3+ (0.2 at. %) and Ce3+ (0.1 at. %) ions, was presented with the conclusion that the relatively low level of doping has no significant boosting impact on the Faraday effect. More comprehensive investigations of dopants and their concentrations are needed in order to assess the benefit of doping of Ho2O3 with RE ions. Improvement of the optical quality is also essential for a future material utilization as an MOE.
Acknowledgements
This work was partially supported by JSPS KAKENHI (Grant No. 15KK0245), and was performed with the support and under the auspices of the National Institute for Fusion Science (KEIN1608). This paper was co-financed by the European Regional Development Fund and the state budget of the Czech Republic (project HiLASE CoE: Grant No. CZ.02.1.010.00.015_0060000674) and by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 739573. This work was also supported by the Ministry of Education, Youth and Sports of the Czech Republic (Programmes NPU I Project No. LO1602, and Large Research Infrastructure Project No. LM2015086).