1 Introduction
Deformable mirrors (DMs) have been used since the 70s in astronomy and high power laser propagation for the correction of the disturbance induced by the atmosphere. Since then, adaptive optics has been successfully exploited in many applications such as ophthalmic imaging, optical free space communications, microscopy and experiments in physics[Reference Tyson and Tyson1]. A comprehensive introduction on recent applications can be found in Ref. [Reference Bonora2]. One of the latest most important applications is in the field of the correction of aberrations in high power lasers. In particular, the wavefront correction due to thermal aberration has become one of the most crucial aspects of the design of high-energy and high-average-power lasers. For this applications, DMs have to be realized with a very high damage threshold to withstand the laser peak energy and a high reflectivity to avoid thermally induced aberrations on the DM itself.
2 Working principle and simulations
2.1 Design parameters
DM design includes the definition of the geometrical specification such as mirror size and shape according to the beam size. Further, the laser driven specifications that significantly influence the coating type such as laser bandwidth, the angle of incidence, damage threshold and dispersion need to be taken into account. Additional design parameters are the required maximum deformation, number and layout of the actuators, the actuator response time and for some applications, the use of vacuum compatible materials.
The design process starts taking into account an estimate of the aberrations in the laser source. The important parameters to be estimated are: maximum required DM deformation (stroke), spatial frequency and temporal evolution of the aberrations. The aberrations can be calculated with simulations[Reference Slezak, Lucianetti, Divoky, Sawicka-Chyla and Mocek3–Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova5] using numerical models or estimated by previous experiments on similar systems[Reference Banerjee, Ertel, Mason, Phillips, Siebold, Loeser, Hernandez-Gomez and Collier6, Reference Sawicka, Divoky, Novak, Lucianetti, Rus and Mocek7].
Figure 1. (a) Slab of active media, (b) heat deposition distribution and thermal effects numerical model results in the form of resulting temperature and OPD distributions.
2.2 Thermo-optical simulations
In the case of multi-slab amplifier[Reference Divoky, Sikocinski, Pilar, Lucianetti, Sawicka, Slezak and Mocek4–Reference Banerjee, Ertel, Mason, Phillips, Siebold, Loeser, Hernandez-Gomez and Collier6], the laser beam is amplified in composite slabs of active media and absorptive cladding which is present for reduction of parasitic oscillations. For example, in the case of the HiLASE laser[Reference Novák, Miura, Smrž, Chyla, Nagisetty, Mužík, Linnemann, Turčičová, Jambunathan, Slezák, Sawicka-Chyla, Pilař, Bonora, Divoký, Měsíček, Pranovich, Sikocinski, Huynh, Severová, Navrátil, Vojna, Horáčková, Mann, Lucianetti, Endo, Rostohar and Mocek8] four numerical models have been developed in order to estimate the thermal effects within the gain media, optical aberrations introduced by the main multi-slab amplifier (see Figure 1) and the wavefront correction. The first model simulates the effect of amplified spontaneous emission (ASE) in the gain media[Reference Sawicka, Divoky, Novak, Lucianetti, Rus and Mocek7]; the second computes the temperature distribution, thermal stresses and estimates the induced optical aberrations[Reference Slezak, Lucianetti, Divoky, Sawicka-Chyla and Mocek3] (see Figure 1(b) for sample result).
The third numerical model simulates the propagation of laser beam in the main laser amplifier by using a laser propagation program for high peak power laser (Miró software[Reference Morice9]) and estimates the output beam characteristics[Reference Divoky, Sikocinski, Pilar, Lucianetti, Sawicka, Slezak and Mocek4]. By using the optical path difference (OPD) estimate from the output of the Miró model, the performance of the DM has been estimated by the fourth numerical model[Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova5].
Among all possible technologies for the realization of DMs, which includes electrostatic membrane[Reference Bonora, Capraro, Poletto, Romanin, Trestino and Villoresi10], piezoelectric bimorph[Reference Fourmaux, Payeur, Alexandrov, Serbanescu, Martin, Ozaki, Kudryashov and Kieffer11] or continuous facesheet with piezostack actuators[Reference Vdovin, Soloviev, Samokhin and Loktev12], electromagnetic[Reference Zawadzki, Jones, Pilli, Balderas-Mata, Kim, Olivier and Werner13] and mechanical actuators[Reference Lefaudeux, Levecq, Escolano and Theis14], the most suitable ones are the piezoelectric (PZT) and mechanical actuators. The reason is that bimorph and piezostack DMs and the mechanical actuators can be realized mounting a high reflectivity high damage threshold dielectric coating. Both piezostack and bimorph DMs offer good performances and the capability of operating with a response time in the order of 1 ms. The stroke of these DMs is usually enough for the application with high power lasers. With respect to piezostack actuators, bimorph DMs have a significant lower price being realized with a single or a patch of few PZT plates. Mechanical actuators DM presents a very high stroke and the advantage of maintaining the shape when switched off but its response time is very slow (in the order of fraction of a second).
2.3 Design technique
In this paper we will take into account the design method of a bimorph DMs. This kind of DMs is composed by a PZT actuator bonded to a thin glass slab[Reference Tyson and Tyson1]. By the application of a voltage across the PZT the actuator bends because of its expansion/contraction against the rigid glass mirror surface. On the face of the PZT electrode can then be created a series of actuators by either chemical etching or laser micromachining.
The mirror surface deformation 
${\it\phi}(x,y)$ can be calculated according to the Poisson equation[Reference Vdovin, Soloviev, Samokhin and Loktev12]:
$$\begin{eqnarray}{\rm\Delta}{\it\varphi}(x,y)=kV(xy),\end{eqnarray}$$ where 
${\rm\Delta}$ is the Laplace operator, 
$V(x,y)$ is the voltage applied on the PZT and 
$k$ is a scaling factor depending on DM construction.
According to the beam size, shape and angle of incidence the DM can be either round, square or elliptical shaped. Following[Reference Vdovin, Soloviev, Samokhin and Loktev12] the initial design rule of thumb are: (1) the number of actuators can be the same of the Zernike modes we aim to correct for and (2) we need a ring of actuators around the area that reflects the laser beam (the so-called active region).
Figure 2(a) shows an example of DM pattern layout for a square laser beam with 36 actuators[Reference Lucianetti, Sawicka, Slezak, Divoky, Pilar, Jambunathan, Bonora, Antipenkov and Mocek15]. The design has to find out the ideal ratio between the area outside the active region ‘SA’ and the active region ‘AR’ with the aim to find the minimum value of SA that gives the desired level of correction.
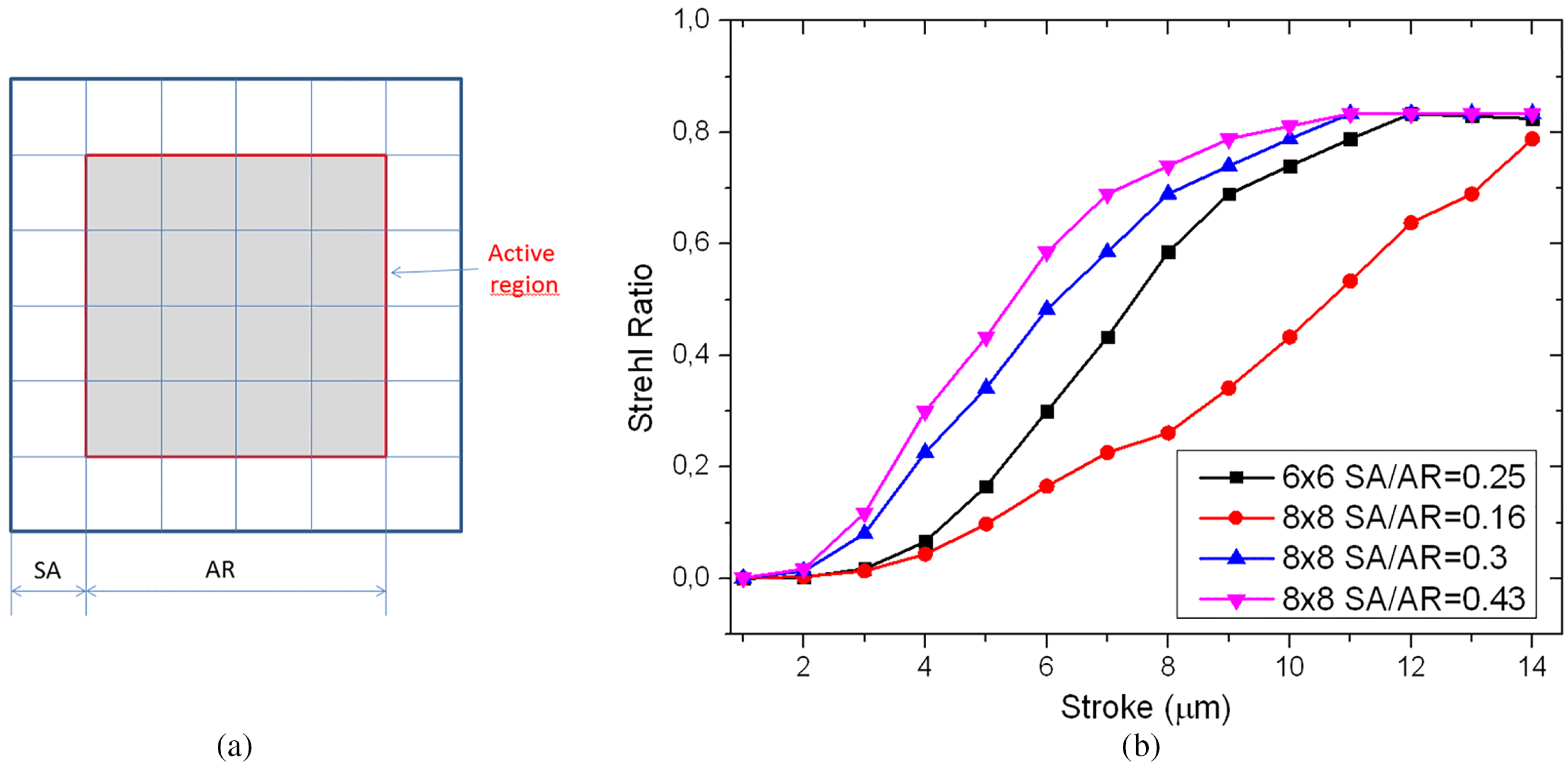
Figure 2. (a) Example of actuators position in a square DM. SA defines the size of the side actuators; AR is the size of the active region (part of the DM illuminated by the laser beam). (b) Reports the Strehl Ratio obtained with the correction of the DM realized in different configurations as reported in the legend in function of the DM stroke.
Calling 
${\it\phi}_{\text{laser}}$ the laser aberration, the analysis can be carried out computing the ability of the DM to correct it for a given actuator pattern (determined by its SA/AR ratio) and maximum deformation (stroke). Equation (1) can be easily solved with either numerical methods or finite difference equations.
The minimum residual root mean square error between 
${\it\phi}_{\text{laser}}$ and the DM shape has been used to calculate the Strehl ratio (
$S$) reported in Figure 2 in function of the stroke (maximum wavefront deformation with all the actuators activated at the maximum voltage) and number of actuators used, according to the formula[Reference Tyson and Tyson1]:
$$\begin{eqnarray}S\approx 1-{\it\phi}_{\text{laser}}^{2}.\end{eqnarray}$$ Note that 
${\it\phi}_{\text{laser}}$ can be calculated by laser modeling Or, for example, by laboratory setups able to replicate thermally induced aberrations. For example, the setup reported in Ref. [Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova5] includes a pump laser and a heat absorbing glass inserted in a cooling system. In this setup, it is possible to study the dynamic formation of the aberrations in function of time, pump energy and cooling conditions. Figure 2(b) reports the results of the DM design applied on a wavefront measured on this setup. The results demonstrate that the 
$6\times 6$ actuators arrangement does not reach a good level of correction while for the 
$8\times 8$ actuators the SA/AR ratio of 0.43 generates a similar correction to the 
$\text{SA}/\text{AR}=0.3$; that is, therefore, the best design choice for this case.
From the knowledge of the stroke requirement determined in Figure 2(b) it is possible to design the DM parameters, both thickness of the glass slab and of the PZT plate. This analysis can be carried out using the bending plate approximation[Reference Timoshenko and Woinowsky-Krieger16]:
$$\begin{eqnarray}C=\frac{d_{31}E_{\max }}{h_{\text{PZT}}}\frac{6kr(1+r)}{1+k^{2}r^{4}+2kr(2+3r+r^{2})},\end{eqnarray}$$ where 
$d_{31}$ is the PZT charge constant, 
$E_{\max }$ is the electric field applied across the PZT, 
$h_{\text{PZT}}$ is the PZT thickness and 
$r$ is the ratio between the glass mirror thickness and the PZT plate, 
$k$ is the ratio between the Young modulus of the glass and the one of the PZT plate and 
$C$ is the mirror curvature (
$C=1/R$, where 
$R$ is the radius of curvature of the DM). On the practical side usually the maximum voltage to be applied to the PZT depends on the voltage amplifier and determines the real limit to the DM deformation. Furthermore, the limit of the ratio between the mirror diameter and thickness (aspect ratio) is limited by practical manufacturing limits to about 25–40. Figure 3 reports the stroke of the DM in function of the mirror thickness and piezo thickness assuming an aspect ratio of 25. As for example the DM Hilase 
$6\times 6$ (see Table 1) has a mirror size of 30 mm, a glass thickness of 0.8 mm and PZT plate thickness of 
$300~{\rm\mu}\text{m}$ (PIC 151).
Figure 3. Stroke in function of glass diameter (with fixed aspect ratio of 25) and PZT thickness with voltage held constant to 150 V.
Table 1. Parameters of the characterized DMs.
2.4 Practical issues
Figure 3 allows to determine the ideal ratio between glass substrate and piezoplate actuator. Some important issues have to be taken into account in the realization of DMs. The very high aspect ratio between the mirror size and thickness is difficult to be reached with an acceptable flatness of the DM. This goal is more difficult with the use of high reflectivity high damage threshold dielectric coatings which induce an additional stress to the DM creating an additional bending. This effect can be reduced by the application of the coating on both sides of the mirror. In addition to substrate flatness other errors may occur in the fabrication process because of the bonding of the mirror to the PZT and to the DM chassis. As a rule of thumb, the deviation from flat has to be corrected using not more that 15%–20% of the entire dynamic range of the DM deformation. To achieve this goal several mounting procedures has been proposed[Reference Rausch, Verpoort and Wittrock17, Reference Hawkes, Collier, Hooker, Reason, Edwards, Hernandez-Gomez, Danson, Ross and Haefner18].
Another important issue is average power which can induce severe thermal stress on the DM. While in the past the cooling of the DM with water has been successfully demonstrated. Recently Veerport et al. [Reference Verpoort, Rausch and Wittrock19] showed that, with the use of coating with a reflectivity higher than 99.998%, it is possible to handle laser beams of several kilowatts without the cooling system. Another different technique is the combined use of thermal and PZT actuators as reported in Ref. [Reference Smith, Phillips, Hooker, Ertel, Mason, Banerjee, Butcher, De Vido, Pilar, Bonora, Greenhalgh, Hernandez-Gomez and Collier20].
3 Experimental results
We present here three different DMs specifically developed for wavefront correction in multi-slab laser amplifiers (see Figure 4).
Figure 4. Pictures of the characterized DMs. (a) Dipole 
$6\times 6$, (b) HiLASE 
$7\times 7$, (c) HiLASE 
$6\times 6$ with the control box.
The mirrors differ slightly in their parameters, as listed in Table 1 columns 1–3 (HiLASE 
$6\times 6$, DiPOLE and HiLASE 
$7\times 7$). They have been tested in terms of achievable magnitude of single Legendre terms, as shown in Figure 5 and compared with the calculated HiLASE aberration determined with the Mirò software. Legendre polynomials have been used instead of the more common Zernike polynomials because they are orthogonal on a square domain and therefore more suitable for square laser beams.
Figure 5. Results of characterization of three DMs in terms of Legendre modes generation capability. The results are compared with the estimated Legendre decomposition of the wavefront of 10 J multi-slab amplifier, which was calculated by the Miró model.
The mirror feasibility as wavefront corrector for multi-slab laser amplifier has been evaluated in several tests including dynamic check of the closed loop, sample aberration generation, far-field improvement capability and damage threshold test. As an example of preliminary test, Figure 6 reports the acquisition of the far-field images obtained by setting as a target aberration of the closed loop the aberration calculated with the thermo-optical simulation of the HiLASE amplifier as reported in Refs. [Reference Slezak, Lucianetti, Divoky, Sawicka-Chyla and Mocek3–Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova5]. Figure 6(b) shows the spot image when the DM has realized the amplifier aberration with an error smaller of 0.08 waves r.m.s. (Maréchal criterion). As term of comparison, Figure 6(c) reports the corrected spot size of the same system. Figure 6(a) compares the cross-sections of both cases. This test is useful to test the performance of the system after the design phase and to measure the residual dynamic range after the correction of the simulated laser aberration. The experimental results confirm that the DM dynamic range is enough for a full correction of the aberrations predicted by the Mirò software.
Figure 6. (a) Cross-section of the spot obtained with by the application of the wavefront calculated with the thermo-optical simulations and after the correction with the closed loop. (b) Spot image of the aberrated wavefront. (c) Spot after the correction with the closed loop operation.
As a result, the DiPOLE 
$6\times 6$ mirror has been successfully implemented into the DiPOLE main laser amplifier. Recently, the HiLASE 
$7\times 7$ mirror has been also implemented into the 10 J amplifier, which is being developed at CLF, RAL, STFC, Harwell, England. The adaptive optics system performed very well decreasing the output wavefront r.m.s. below 40 nm[Reference Reinlein, Appelferlder, Goy, Ludewigt and Tunnermann21, Reference Bonora, Divoky, Phillips, Smith, Ertel, Collier, Jelinkova, Lucianetti and Mocek22].
The same technology and design principle can be used to realize DMs for different type of laser sources with different size and angle of incidence. To give an overview of some DM recently realized for femtosecond Ti:Sa laser and carbon dioxide, Table 1 columns 4–6 (Femto1, CO2, Femto45) shows the properties of these different DMs. In particular, for femtosecond lasers it is of fundamental importance to have a very high reflectivity on a very broad bandwidth with a low dispersion.
3.1 Deformable mirror control
Another fundamental aspect of an adaptive optics system is the control. In laser systems the most used control strategy is the closed loop feedback with the use of a wavefront sensor. The effectiveness of this method in high power laser technology has been demonstrated in many publications; see for example Ref. [Reference Fourmaux, Payeur, Alexandrov, Serbanescu, Martin, Ozaki, Kudryashov and Kieffer11]. The control system is based on a negative feedback loop with an integrative controller to achieve a fast response with a good stability and rejection of detrimental effects such as noise in the characterization and actuator nonlinearities such as the hysteresis. Among possible wavefront sensors, both Hartmann and Shack Hartmann have been successfully implemented. Another important wavefront sensor is the lateral shearing interferometer (SID4, Phasis S.A.); see for example Refs. [Reference Reinlein, Appelferlder, Goy, Ludewigt and Tunnermann21–Reference Wattellier, Fuchs, Zou, Abdeli, Haefner and Pépin23]. Usual frame rate of these types of wavefront sensors is in the order 15–100 Hz on a laptop without the use of specific hardware such as a digital signal processor[Reference Mocci, Bonora and Muradore24] or a field programmable gate array. In most of the cases, the laser aberrations are generated by heat accumulation and have a much slower time variation[Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova5] and therefore a fast time control is not necessary.
The design methodology presented previously in the paper assumed the DM as a linear device and its response as represented in Equation (1). These modeling results allow designing the DM but it does not give any information about the DM behavior together with the wavefront sensor and do not allow to test the control algorithm. Recently, Pilar et al. [Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova5] proposed an experimental simulation method of the entire closed loop system based on the use of a photocontrolled DM. With this method, it is possible to simulate any arbitrary DM actuator quantity and disposition and its ability to correct for aberrations together with different wavefront sensors.
3.2 Electronic control driver
An additional important aspect is the electronic driver control[Reference Bonora, Capraro, Poletto, Romanin, Trestino and Villoresi10]. PZT actuators have to be operated with the application of a high voltage for each actuator. All the DMs listed in Table 1 works with the application of a voltage in the range of 
$\pm 125$ V. Recent advances in electronic components allowed the realization of the control box in a small compact unit (see Figure 4(b)) that is possible to be integrated inside the DM chassis.
3.3 Conclusions
In conclusion, we presented the design criteria, manufacturing rules and preliminary tests for the realization of DMs for high power solid-state diode pumped lasers. In addition, we show that the same principles can be applied to the realization of DMs for different lasers such as femtosecond laser source and CW carbon dioxide lasers.
Acknowledgments
The authors thank Matteo Negro, Caterina Vozzi and Salvatore Stagira for discussions and damage threshold measurements. This work is co-financed by the European Regional Development Fund, the European Social Fund and the state budget of the Czech Republic (project HiLASE: CZ.1.05/2.1.00/01.0027, project DPSSLasers: CZ.1.07/2.3.00/20.0143). This research was partially supported by the grant RVO 68407700.
Open access
