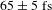1 Introduction
Pulsed femtosecond laser damage studies are crucial for many applications of high-energy physics[Reference Huang and Byer1], medical therapy[Reference England, Noble, Fahimian, Loo, Abel, Hanuka and Schachter2] and fabrication of precise micro-structures[Reference Liu, Du and Mourou3]. It is particularly vital for systems that are expected to operate for years without replacing their crucial component, as is the case with advanced laser-driven particle acceleration schemes. A defining measure in this context is the damage threshold fluence (DTF) of the material, being calculated as the energy per surface area unit that the material can sustain without experiencing irreversible damage to its optical properties. DTF dependences on single pulse duration[Reference Stuart, Feit, Herman, Rubenchik, Shore and Perry4], on wavelength[Reference Carr, Radousky and Demos5] and on material band gap[Reference Mero, Liu, Rudolph, Ristau and Starke6] have been investigated extensively and are reasonably well characterized. For low-loss dielectrics, e.g., silica (
$\text{SiO}_{2}$
), at single pulse operation, the typical value of DTF is a few
$\text{J}/\text{cm}^{2}$
for a sub-picosecond long pulse[Reference Chimier, Utéza, Sanner, Sentis, Itina, Lassonde, Légaré, Vidal and Kieffer7]. Much higher values of DTF (
$100~\text{J}/\text{cm}^{2}$
), when operating at UV nanosecond pulses, were reported for chemically etched fused silica[Reference Bude, Miller, Baxamusa, Shen, Laurence, Steele, Suratwala, Wong, Carr, Cross and Monticelli8, Reference Laurence, Bude, Ly, Shen and Feit9].
For cases in which the same spot is exposed to multiple shots, several experiments showed that the DTF is lower as compared with a single shot[Reference Jee, Becker and Walser10–Reference Mannion, Magee, Coyne, OConnor and Glynn14]. This effect, known as incubation, was mostly investigated in metals, for pulse durations which vary between nanoseconds and femtoseconds. In addition, various features were examined at low or high repetition rate[Reference Di Niso, Gaudiuso, Sibillano, Mezzapesa, Ancona and Lugarà11, Reference Mouskeftaras, Guizard, Fedorov and Klimentov15], and a power-law relation was proposed to describe the DTF dependence on the number of laser shots. However, only a few groups considered incubation operating with sub-picosecond pulses in dielectrics[Reference Lenzner, Krüger, Sartania, Cheng, Spielmann, Mourou, Kautek and Krausz16–Reference Zhang, Jiang, Li, Shi, Yu, Qu and Lu23], especially fused silica which plays a crucial role in a variety of high power optical components[Reference Roth, Tsitrone, Loarte, Loarer, Counsell, Neu, Philipps, Brezinsek, Lehnen, Coad, Grisolia, Schmid, Krieger, Kallenbach, Lipschultz, Doerner, Causey, Alimov, Shu, Ogorodnikova, Kirschner, Federici and Kukushkin24, Reference Peralta and Byer25]. When comparing the experimental accumulation dependence in different studies one should keep in mind that, except for the various metrics examined (laser wavelength, pulse duration and pressure), the method for establishing the damage criterion and the exposure method differ from one study to another. Therefore special attention should be given to the latter two.
First, with regards to the damage criterion, DTF is mostly determined ex situ by extrapolating the visible geometrical damage observed with an optical Nomarski microscope[Reference Allen, David and Nomarski26] or a scanning electron microscope[Reference Nixon27]. However, an online detection system is required in order to measure an accumulative process in real time in situ. While some studies utilized an in situ online camera[Reference Li, Zhao, Cui, Wang, Peng, Shan, Zhu, Wang and Shao28], in this study we monitor a probe laser by a shielded silicon photo-detector with a narrow bandpass filter.
Second, with regards to the exposure method, most studies rely on exposing the sample to a fixed number of laser shots – either of increasing energy levels[Reference Soong, Byer, Colby, England and Peralta29] or a fixed energy level per pulse[Reference Bonse, Wrobel, Krüger and Kautek20, Reference Nguyen, Emmert, Schwoebel, Patel, Menoni, Shinn and Rudolph30] – within the same measurement. The accumulation process will of course differ from one method to another. In this study what we conceive to be the ideal way to measure a time-dependent process is to accumulate pulses over time while the energy per pulse is fixed. The DTF resulting from our technique will be different from the former two. In this study, we present the first comprehensive in situ measurement of damage as a function of accumulated pulses, using time-resolved acquisition system, namely, accumulating pulses with a fixed fluence per pulse, until damage occurs.
Our experimental efforts were accompanied by theoretical studies. These indicate that at picosecond time scales and below, the major mechanism of a single ultrashort laser-pulse damage is initiated by photo-ionization that elevates electrons from the valence to the conduction band of the material. Typical thermalization time, required for the electrons to transfer energy back to the lattice in the form of heat, is of the order of 2–10 ps[Reference Sun, Jiang, Liu, Zhou, Yang and Gong31]. For femtosecond pulses, the excited conduction electrons do not have enough time to thermalize with the lattice. Therefore, it has been suggested that damage occurs via an avalanche ionization[Reference Zhang, Jiang, Li, Shi, Yu, Qu and Lu23] or a resonance between the plasma frequency of the electrons and the angular frequency of the illuminating laser, producing a surface ablation[Reference Soong, Byer, Colby, England and Peralta29, Reference von der Linde and Schuler32, Reference Soong, Byer, McGuinness, Peralta and Colby33]. In the latter studies the rate at which electrons are photo-ionized was described by the Keldysh model[Reference Keldysh34].
The theory of a single pulse DTF is irrelevant for the multiple pulse case. It is virtually impossible for a femtosecond-scale process (or even picosecond) such as the ultrashort laser-pulse-induced damage threshold mechanism described above to explain the accumulative process which occurs at the scale of milliseconds. A general comprehensive theory has yet to be developed, but qualitatively, the decrease in the damage threshold with multi-pulse irradiation was attributed to the accumulation of laser-induced chemical and structural changes of the material, plastic deformation of the surface[Reference Jee, Becker and Walser10, Reference Mannion, Magee, Coyne, OConnor and Glynn14], thermal or bulk photo-thermal model[Reference Anisimov, Bityurin, Luk’yanchuk and Peled35]. Other models[Reference Emmert, Mero and Rudolph36–Reference Negres, Feit and Demos38] explain the incubation effect[Reference Sun, Lenzner and Rudolph39] by accumulation of occupied defect and mid-gap trap states during the pulse train, since the relaxation of electrons from defect states to the valence band is on a time scale of milliseconds. Although the effect of the repetition rate was also investigated, the mechanism is still unclear, and effects like heat dissipation or charged particles expelled outside the lattice must be examined.
In this study we demonstrate that the DTF decreases as the number of pulses increases. Damage is detected in a real-time ‘pump–probe’ setup. The accumulative effect on the DTF is investigated in various configurations: vacuum (0.4 mTorr) or STP, smooth surface or grating, and at two different repetition rates (10 or 600 Hz). Although the relation to underlying deterministic theories is not yet understood, we suggest our own phenomenological model whereby all experimental data can be described in terms of four parameters: three of which are extrinsic and account for the various conditions mentioned above, and one intrinsic which is globally defined and is a characteristic of the material.
2 Experimental setup
The backbone of the experiment consists of a ‘pump–probe’ measurement, described in details in Ref. [Reference Hanuka, Schächter, Wootton, Wu, Soong, Makasyuk and England40]. Three types of fused silica samples were tested: wafer, un-bonded and bonded grating structures. The wafer is a thin planar bulk, and while the un-bonded structure is a wafer which contains a periodic nano-grating structure on one side, the bonded structure[Reference Peralta and Byer25] is two of these with a vacuum channel of
$0.8~\unicode[STIX]{x03BC}\text{m}$
between the gratings. The grating structures contribute to local field enhancements, and thus might decrease the structure’s damage tolerance. Therefore the fluence is expected to be higher for the half un-bonded rather than the bonded grating. Each grating sample was cleaned with methanol, and unless stated otherwise, the wafer samples were also cleaned in an ultrasonic bath. In all cases the laser was focused on the sample’s planar (rather than patterned) surface. For each sample, we tested hundreds of sites at which laser fluence was varied from site to site. At each test site we held a fixed laser fluence per pulse and laser pulses were accumulated until damage was detected. The damage criterion was adopted to be 10% change in the HeNe’s intensity, which is well above the noise level of the measurement. Also, we observed the damaged site using an online CCD camera.
3 Results
To guarantee that the accumulative process of multiple laser pulses is accurately captured, we repeat the damage experiment for a fixed laser fluence several (7–10) times. We exclude in our analysis sites where the IR energy fluctuated, and a single pulse peaked above the noise level. In these cases not the accumulated pulses but the peak single pulse causes immediate damage. Additionally, to ensure the integrity of the experimental data, we analyze each sample with an optical microscope after the damage test. We confirm that the sites registered as damaged show visible damage under microscope. Finally, we note that our reported DTF values correspond to peak laser fluence, calculated as
$$\begin{eqnarray}F_{th}=\frac{2U_{th}}{\unicode[STIX]{x1D70B}w_{x}w_{y}},\end{eqnarray}$$
where
$U_{th}$
is the laser-pulse energy and
$w_{x},w_{y}$
are the rms Gaussian diameters. The transverse spot size of the laser beams, as measured in the sample’s plane using knife-edge scans, was
$60~\unicode[STIX]{x03BC}\text{m}$
.
Figure 1 shows the measured number of pulses (
$n_{sh}$
) that the material is exposed to when damage occurs for a preset fluence, in various operating conditions (sample, vacuum/air and repetition rate). Repetition rate of 10 Hz was used for low number of shots
$(n_{sh}<10^{3})$
measurements, while for longer ones we used a 600 Hz repetition rate. With this range of repetition rates in the fs regime, the fluence has weak dependence on the repetition rate[Reference Emmert, Mero, Nguyen, Rudolph, Patel, Krous and Menoni41]. In spite of this limitation, the trend is clear: DTF decreases as number of shots increases. The vertical error bars represent small fluctuations in the laser-pulse energy, and the horizontal error bars represent variations in the observed number of shots for repeated measurements. Moreover, the solid curves represent an empirical fitting according to Equation (2).
Figure 1. Measured number of pulses where damage occurred for each fixed laser fluence. (a) 10 and 600 Hz measurements with wafer (W) samples in air and vacuum (A/V). (b) 600 Hz measurements with two types of structures: grating bonded (G) and half grating un-bonded (H), each in air and vacuum. The solid curves represent an empirical fitting according to Equation (2).
Operating with a repetition rate of 600 Hz, silica bonded grating in vacuum has the lowest DTF, whereas silica bonded grating in air has a DTF greater by a factor of two for low number of shots; but this difference is diminished for high number of shots. The DTF of half un-bonded grating structure in vacuum is in between of the above two. Silica wafer in air has the highest threshold as it does not contain features which contribute to local field enhancements, thus increasing the structure’s damage tolerance. When the wafer is in vacuum it has a similar DTF to grating in air, but lower than wafer in air. We therefore may conclude that both the environment and the geometry of the sample affect the damage threshold. This is consistent with previous experiments[Reference Rosenfeld, Lorenz, Stoian and Ashkenasi18] which showed that multi-shot damage in vacuum for silica is lower since there is no ambient oxygen available for replenishing the
$\text{O}_{2}$
removed from the material by the laser[Reference Nguyen, Emmert, Schwoebel, Patel, Menoni, Shinn and Rudolph30, Reference Takigawa, Kurosawa, Sasaki, Yoshida, Fujiwara and Kato42].
The DTF of a wafer cleansed with methanol followed by ultrasonic bath is higher by a factor of two compared to a wafer cleansed only with methanol. This difference is less pronounced at low fluence or equivalently for high number of shots (
$n_{sh}>10^{4}$
). Although further research is required to understand the contribution of the surface morphology, this result is consistent with a recent work[Reference Bude, Miller, Baxamusa, Shen, Laurence, Steele, Suratwala, Wong, Carr, Cross and Monticelli8] that suggests that at low fluence the DTF’s dominant precursors are fracture-induced electronic defects. These can be eliminated by an advanced mitigation process, thereby increasing the DTF. At higher fluence, the DTF’s dominant precursors are impurities caused during chemical processing. Minimizing those impurities would enable to reach the intrinsic DTF of the material itself[Reference Negres, Feit and Demos38]. Therefore it is expected that cleansing the wafer will have greater effect at high fluence, as was observed in this study.
Moreover, although damage detection and exposure methods vary between groups, our findings are consistent with some prior results: in Ref. [Reference Du, Liu, Korn, Squier and Mourou22], using visible damage technique, the wafer’s DTF of a single shot (780 nm, 100 fs) was
$11~\text{J}/\text{cm}^{2}$
in air, as is in our study. However, in Ref. [Reference Soong, Byer, Colby, England and Peralta29], for different exposure methods, employing longer pulse duration (800 nm, 1 ps, 600 Hz), and
$5\times 10^{4}$
shots, the wafer’s DTF in situ was 3.45 and
$2~\text{J}/\text{cm}^{2}$
in air and vacuum, respectively, as compared to 0.7 and
$0.4~\text{J}/\text{cm}^{2}$
in our study.
As shown in Figure 1(a), for higher fluence values the damage accumulative process is even more pronounced and a significant decrease is observed for both environmental conditions: air and vacuum. For low number of shots (obtained at 10 Hz), wafer in vacuum has lower DTF than wafer in air; both are fitted to the corresponding measurements at 600 Hz according to Equation (2). It is important to note that since different nonlinear processes might affect the fluence for different values of number of shots, the behavior of the 10 Hz air and vacuum curves might follow different scaling. In order to emphasize the latter, both were plotted for the same model (Equation (2)); this might explain the slight deviation of the 10 Hz measurements for
$n_{sh}=1000$
. For a significantly high number of shots (e.g.,
$n_{sh}>10^{5}$
), the fluence threshold is up to one order of magnitude lower than irradiation with a few shots, and it seems to saturate at a different constant value
$F_{\infty }$
for each experimental condition, as shown in Figure 1(b). This behavior is consistent with the suggested incubation models, where the multi-shot threshold fluence is not lowered by further increasing the number of laser shots[Reference Di Niso, Gaudiuso, Sibillano, Mezzapesa, Ancona and Lugarà11, Reference Ashkenasi, Lorenz, Stoian and Rosenfeld17].
Figure 2. DTF’s quasi-intrinsic parameter as a function of logarithmic number of shots. DTF does not depend on the configuration (intrinsic) below a critical number of shots
$n_{cr}$
; but above this point the asymptotic DTF’s value depends on the configuration (extrinsic).
4 Discussion
Analysis of the experimental data indicates that the DTF decrease with the increase of the number of shots
$n_{sh}$
follows the equation
$$\begin{eqnarray}F_{th}(n_{sh})=\left\{\begin{array}{@{}ll@{}}F_{1}-\unicode[STIX]{x0394}F(\ln n_{sh})^{p} & n_{sh}\leqslant n_{cr},\\ F_{\infty } & n_{sh}\geqslant n_{cr},\end{array}\right.\end{eqnarray}$$
where
$F_{1}$
is the single shot DTF,
$\unicode[STIX]{x0394}F$
represents the slope of the dependence on the number of shots, and
$n_{cr}=\exp \{[(F_{1}-F_{\infty })/\unicode[STIX]{x0394}F]^{1/p}\}$
is the critical number of shots; after which the fluence reaches an asymptotic value of
$F_{\infty }$
. Our analysis indicates that
$F_{1}$
,
$\unicode[STIX]{x0394}F$
,
$F_{\infty }$
are extrinsic parameters, dependent on the operating conditions (repetition rate, sample’s configuration and environment), whereas the power
$p$
is an intrinsic variable, independent of the experimental conditions.
In order to determine the values of
$p$
,
$F_{\infty }$
, and
$n_{cr}$
we employ a nonlinear minimum error approach. The essentials of the approach could be summarized into three steps; the first two steps are performed separately for each set of experimental data
$s$
, whereas the third step considers all sets of experiments. In step 1, for given values of
$p$
and
$n_{cr}$
, we determine the optimal values of the extrinsic parameters
$F_{1}$
and
$\unicode[STIX]{x0394}F$
. In step 2, we repeat the former step for various values of
$n_{cr}$
, and we minimize the normalized mean squared error
$\unicode[STIX]{x1D700}_{s}(p)$
for any given
$p$
, and for each experimental set
$s$
. In step 3, we repeat steps 1 and 2 for all sets of configurations and experiments, namely minimizing the global error
$\sum _{s}\unicode[STIX]{x1D700}_{s}(p)$
for a given
$p$
.
The described nonlinear minimum error approach reveals that for all the experiments, the global error is less than
$0.5\%$
, and the power
$p$
varies by
$0.4\pm 0.07$
. Typical values of
$F_{\infty }$
were found in the range between 0.13 and 0.7 J/cm
$^{2}$
, and
$n_{cr}$
in the range of
$3\times 10^{4}-2\times 10^{5}$
pulses.
The proposed model differs from other similar models in Refs. [Reference Di Niso, Gaudiuso, Sibillano, Mezzapesa, Ancona and Lugarà11, Reference Ashkenasi, Lorenz, Stoian and Rosenfeld17]. While the former assumes a logarithmic dependence on the number of shots, the latter assumes a power-law dependence
$F_{th}=F_{\infty }-(F_{\infty }-F_{1})n_{sh}^{\unicode[STIX]{x1D709}-1}$
where
$\unicode[STIX]{x1D709}$
is an incubation coefficient. This incubation coefficient is similar to the parameter
$p$
in Equation (2), thereby appearing to be intrinsic. However our model better fits the experimental data as compared with the power-law model (errors of
$0.5\%$
and
$5\%$
, respectively).
Figure 1 reveals the general trend – DTF decreases as the number of shots increases. However, a deeper insight could be obtained by defining the quasi-intrinsic (normalized) DTF
$F_{qi}$
for each experiment,
$$\begin{eqnarray}F_{qi}\equiv \left(\frac{F_{1}-F_{th}}{\unicode[STIX]{x0394}F}\right)^{1/p}=\left\{\begin{array}{@{}ll@{}}\ln n_{sh} & n_{sh}\leqslant n_{cr}\\ \ln n_{cr} & n_{sh}>n_{cr}\end{array}\right..\end{eqnarray}$$
Equation (3) shows that the DTF does not depend on the configuration (intrinsic) below the critical number of shots
$n_{cr}$
; but above this point the asymptotic DTF’s value depends on the configuration (extrinsic). This result is clearly revealed in Figure 2 for
$p=0.4$
. The low (high)
$n_{cr}$
values indicate that the system may operate for 45 (5) min continuously without damage. Alternatively, for a pre-selected operation time the fluence could be tuned below the DTF. It should be pointed out that the range of repetition rates employed here is fairly limited. We assume that for higher repetition rates (
${\sim}$
100 MHz),
$F_{\infty }$
might have a weak dependence on the number of shots. However, we cannot predict this dependency based on the current experimental data.
In addition to monotonic multi-shot exposure, we have exposed the same site to the IR laser in more than one session with a break of a few minutes in between. In all cases the site was not damaged after the first exposure. Re-exposure at the same fluence level, sometimes resulted in higher accumulated number of shots before damage has occurred. This might be conceived as a preliminary indication of the material’s ‘long-term memory’, which could be utilized for structure’s ‘baking’ in due course, similarly to what has been done in microwave accelerators.
5 Conclusion
In conclusion, we have experimentally demonstrated that the DTF of fused silica varies with the accumulated number of femtosecond laser shots. Based on the experimental data we were able to develop a model which indicates that the DTF varies with the number of shots like
$(\ln n_{sh})^{p}$
up to a critical point (
$n_{sh}\leqslant n_{cr}$
); above this point the DTF reaches an asymptotic value
$F_{\infty }$
, which ranges between 0.7 and
$2~\text{J}/\text{cm}^{2}$
, depending on the exposure time. These values correspond to maximum accelerating gradients of
$6.5{-}10~\text{GV}/\text{m}$
[Reference Hanuka and Schächter43].
Both DTFs for a single shot
$(F_{1})$
and the asymptotic value
$(F_{\infty })$
, and the critical number of shots
$(n_{cr})$
are extrinsic parameters, which depend on the configuration (repetition rate, pressure and geometry near or at the surface). The results provide some evidence that the power of this dependence
$(p=0.4)$
does not depend on the experimental conditions that were systematically varied in this research. However,
$p$
may depend on other experimental conditions which remained constant (laser wavelength, material composition or surface preparation).
Our experimental data supports damage accumulation over milliseconds. The physical mechanism is still somewhat unclear, and effects like heat dissipation or charged particles expelled outside the lattice should be considered; however these are beyond the scope of this study.
Acknowledgements
This work was supported by the U.S. Department of Energy under Contracts DE-AC02-76SF00515 (SLAC) and Israel Science Foundation. The authors acknowledge A. Ceballos for providing the wafer samples, E. Peralta for fabricating the grating samples, and K. Leedle for building the vacuum chamber.
Open access
