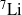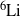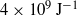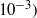1. Introduction
Table-top nuclear fusion in the chemical physics laboratory[Reference Jortner and Last1,Reference Heidenreich, Last and Jortner2] was realized by nuclear fusion driven by Coulomb explosion (NFDCE) of assemblies of nanostructures, i.e., clusters (with initial radii ![]() ${R}_{0} = 1{\unicode{x2013}} 10~\mathrm{nm} $)[Reference Zweiback, Smith, Cowan, Hays, Wharton, Yanovsky and Ditmire3–Reference Li, Liu, Ni, Li and Xu15], and nanodroplets (with
${R}_{0} = 1{\unicode{x2013}} 10~\mathrm{nm} $)[Reference Zweiback, Smith, Cowan, Hays, Wharton, Yanovsky and Ditmire3–Reference Li, Liu, Ni, Li and Xu15], and nanodroplets (with ![]() ${R}_{0} = 10{\unicode{x2013}} 500~\mathrm{nm} $)[Reference Li, Liu, Ni, Li and Xu15–Reference Last, Peano, Jortner and Silva20], which are driven by ultraintense femtosecond near-infrared lasers[Reference Madison, Patel, Allen, Price, Fitzpatrick and Ditmire7,Reference Lu, Liu, Wang, Wang, Zhou, Deng, Xia, Xu, Lu, Jiang, Leng, Liang, Ni, Li and Xu8,Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17] . The ultraintense laser pulses for generating Coulomb explosion (CE) of such nanostructures are characterized by ultrahigh intensities of up to
${R}_{0} = 10{\unicode{x2013}} 500~\mathrm{nm} $)[Reference Li, Liu, Ni, Li and Xu15–Reference Last, Peano, Jortner and Silva20], which are driven by ultraintense femtosecond near-infrared lasers[Reference Madison, Patel, Allen, Price, Fitzpatrick and Ditmire7,Reference Lu, Liu, Wang, Wang, Zhou, Deng, Xia, Xu, Lu, Jiang, Leng, Liang, Ni, Li and Xu8,Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17] . The ultraintense laser pulses for generating Coulomb explosion (CE) of such nanostructures are characterized by ultrahigh intensities of up to ![]() $1{0}^{21} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, which can be produced from the currently available Terawatt and Pentawatt lasers[Reference Morou, Tajima and Bulanov21]. The interaction of ultraintense femtosecond near-infrared lasers with nanometer-sized matter[Reference Heidenreich, Last and Jortner2–Reference Last, Peano, Jortner and Silva20] results in inner and outer ionization of the nanostructures[Reference Last and Jortner22–Reference Last and Jortner24] followed by CE, which produces high-energy (10 keV–15 MeV) ions in the energy domain of nuclear physics. Previous studies of NFDCE of clusters[Reference Heidenreich, Last and Jortner2–Reference Li, Liu, Ni, Li and Xu15] and of nanodroplets[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17–Reference Last, Peano, Jortner and Silva20,Reference Last and Jortner24] involved nuclear reactions inside or outside the macroscopic plasma filament, which is produced by an assembly of Coulomb-exploding nanostructures within the focal volume of the laser.
$1{0}^{21} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, which can be produced from the currently available Terawatt and Pentawatt lasers[Reference Morou, Tajima and Bulanov21]. The interaction of ultraintense femtosecond near-infrared lasers with nanometer-sized matter[Reference Heidenreich, Last and Jortner2–Reference Last, Peano, Jortner and Silva20] results in inner and outer ionization of the nanostructures[Reference Last and Jortner22–Reference Last and Jortner24] followed by CE, which produces high-energy (10 keV–15 MeV) ions in the energy domain of nuclear physics. Previous studies of NFDCE of clusters[Reference Heidenreich, Last and Jortner2–Reference Li, Liu, Ni, Li and Xu15] and of nanodroplets[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17–Reference Last, Peano, Jortner and Silva20,Reference Last and Jortner24] involved nuclear reactions inside or outside the macroscopic plasma filament, which is produced by an assembly of Coulomb-exploding nanostructures within the focal volume of the laser.
NFDCE constitutes the table-top conversion of laser energy to nuclear energy. We advance theoretical–computational methods to establish the conditions for the attainment of high efficiencies for table-top conversion of laser energy to nuclear energy mediated by CE dynamics of molecular nanodroplets. A source–target design[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] for fusion of D with ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, and D atoms attains the highest table-top fusion efficiencies (
${}^{6} \mathrm{Li} $, and D atoms attains the highest table-top fusion efficiencies (![]() ${\sim }1{0}^{9} ~{\mathrm{J} }^{- 1} $ per laser pulse) obtained to date. The data for high-efficiency table-top laser energy
${\sim }1{0}^{9} ~{\mathrm{J} }^{- 1} $ per laser pulse) obtained to date. The data for high-efficiency table-top laser energy ![]() $\rightarrow $ nuclear energy conversion are comparable to those obtained to date for ‘big science’ inertial fusion setups[Reference Dittrich, Hammel, Keane, McEachren, Tuner, Haan and Suter27–Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30].
$\rightarrow $ nuclear energy conversion are comparable to those obtained to date for ‘big science’ inertial fusion setups[Reference Dittrich, Hammel, Keane, McEachren, Tuner, Haan and Suter27–Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30].
2. The source–target design for table-top fusion
Our exploration of the maximization of table-top fusion yields[Reference Ron, Last and Jortner26] established that an increase of the table-top fusion efficiencies by 3–5 orders of magnitude for NFDCE of nanodroplets, relative to those attained inside or outside a plasma filament[Reference Heidenreich, Last and Jortner2,Reference Madison, Patel, Price, Edens, Allen, Cowan, Zweiback and Ditmire6,Reference Madison, Patel, Allen, Price, Fitzpatrick and Ditmire7,Reference Last and Jortner11,Reference Last and Jortner19,Reference Heidenreich, Last, Jortner, Kühn and Wöste23] , can be attained by transcending the macroscopic plasma filament as a reaction medium for table-top fusion and by considering a source–target design, which was advanced in our previous work[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] , with the following operational conditions.
(1) The source–target design is based on the selection of an appropriate source (where high-energy deuterons or protons are produced by CE) and a target (where the fusion reaction occurs). For fusion between two distinct nuclei, high-energy deuterons (or protons) are produced with the source by CE of homonuclear deuterium or hydrogen nanodroplets[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] . The ions react with a solid target of the second reagent.
(2) Regarding the properties of the source within the source–target design, a key element for efficient fusion rests on the production of high-energy (up to 15 MeV) deuterons or protons[Reference Last and Jortner24].
(3) The beneficial properties of the cylindrical hollow solid target within the source–target design originate from the efficient collection of high-energy deuterons and protons from the source, together with the moderately low stopping power and large penetration depth of deuterons within the solid[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] .
3. Table-top fusion yields
High table-top fusion yields were calculated for reactions of deuterons with several light nuclei, i.e., ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, and D, within the source–target reaction design[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] . The source consists of deuterons produced by CE of deuterium nano-droplets,
${}^{6} \mathrm{Li} $, and D, within the source–target reaction design[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] . The source consists of deuterons produced by CE of deuterium nano-droplets, ![]() ${R}_{0} = 70{\unicode{x2013}} 300~\mathrm{nm} $), impinging on a hollow solid cylinder target containing the
${R}_{0} = 70{\unicode{x2013}} 300~\mathrm{nm} $), impinging on a hollow solid cylinder target containing the ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, and D atoms. The fusion reactions with the highest cross sections in the relevant energy domains[Reference Rose and Clark31–Reference Eliezer, Henis and Martinez-Val33] were considered. The cylindrical solid target involves
${}^{6} \mathrm{Li} $, and D atoms. The fusion reactions with the highest cross sections in the relevant energy domains[Reference Rose and Clark31–Reference Eliezer, Henis and Martinez-Val33] were considered. The cylindrical solid target involves ![]() ${}^{7} \mathrm{Li} $ or
${}^{7} \mathrm{Li} $ or ![]() ${}^{6} \mathrm{Li} $ (pure metal or LiF ionic solid) for reactions of D with Li isotopes, and low-temperature (
${}^{6} \mathrm{Li} $ (pure metal or LiF ionic solid) for reactions of D with Li isotopes, and low-temperature (![]() $T\lt 20~\mathrm{K} $) deuterium film or deuterated
$T\lt 20~\mathrm{K} $) deuterium film or deuterated ![]() $({\mathrm{CD} }_{2} )$ polymer polyethylene[Reference Heidenreich, Last and Jortner2,Reference Davis, Petrov and Velikovich13,Reference Ron, Last and Jortner26] at room temperature for the
$({\mathrm{CD} }_{2} )$ polymer polyethylene[Reference Heidenreich, Last and Jortner2,Reference Davis, Petrov and Velikovich13,Reference Ron, Last and Jortner26] at room temperature for the ![]() $\mathrm{D} {+ }\mathrm{D} $ reaction.
$\mathrm{D} {+ }\mathrm{D} $ reaction.
The fusion reaction yield ![]() $Y$ per laser pulse is
$Y$ per laser pulse is
where ![]() $N$ is the number of deuterons produced from the source and
$N$ is the number of deuterons produced from the source and ![]() $\langle y\rangle $ is the average reaction probability:
$\langle y\rangle $ is the average reaction probability:
Here ![]() $P(E)$ is the energy distribution function of the ions with a maximal energy
$P(E)$ is the energy distribution function of the ions with a maximal energy ![]() ${E}_{\max } $, obtained from scaled electron and ion dynamics (SEID) simulations described in our previous work[Reference Last and Jortner24,Reference Last and Jortner34,Reference Last and Jortner35] , and
${E}_{\max } $, obtained from scaled electron and ion dynamics (SEID) simulations described in our previous work[Reference Last and Jortner24,Reference Last and Jortner34,Reference Last and Jortner35] , and ![]() $y(E)$ is the reaction probability per ion with an initial energy
$y(E)$ is the reaction probability per ion with an initial energy ![]() $E$ penetrating into the solid target, given by
$E$ penetrating into the solid target, given by
where ![]() $\sigma (E)$ is the reaction cross section[Reference Rose and Clark31–Reference Eliezer, Henis and Martinez-Val33] and
$\sigma (E)$ is the reaction cross section[Reference Rose and Clark31–Reference Eliezer, Henis and Martinez-Val33] and ![]() $S(E)$ is the stopping power normalized to the atomic density of the target[Reference Andersen and Ziegler36]. The energy dependence of
$S(E)$ is the stopping power normalized to the atomic density of the target[Reference Andersen and Ziegler36]. The energy dependence of ![]() $y(E)$ (inset to Figure 1 ) over the relevant energy domain up to 15 MeV (which corresponds to the CE energies) is determined by the cumulative contributions of
$y(E)$ (inset to Figure 1 ) over the relevant energy domain up to 15 MeV (which corresponds to the CE energies) is determined by the cumulative contributions of ![]() $\sigma (E)$ and
$\sigma (E)$ and ![]() $S(E)$.
$S(E)$. ![]() $y(E)$ exhibits a nearly power-law dependence on
$y(E)$ exhibits a nearly power-law dependence on ![]() $E$ (inset to Figure 1), in the form
$E$ (inset to Figure 1), in the form
where ![]() $b$ is a constant and
$b$ is a constant and ![]() $\xi $ is a scaling parameter. The data of the inset to Figure 1 result in
$\xi $ is a scaling parameter. The data of the inset to Figure 1 result in ![]() $\xi = 1. 8\pm 0. 3$ for
$\xi = 1. 8\pm 0. 3$ for ![]() $\mathrm{D} {+ }\mathrm{D} $,
$\mathrm{D} {+ }\mathrm{D} $, ![]() $\xi = 2. 2\pm 0. 7$ for
$\xi = 2. 2\pm 0. 7$ for ![]() $\mathrm{D} {+ }{\text{} }^{7} \mathrm{Li} $ and
$\mathrm{D} {+ }{\text{} }^{7} \mathrm{Li} $ and ![]() $\xi = 2. 9\pm 0. 7$ for
$\xi = 2. 9\pm 0. 7$ for ![]() $\mathrm{D} {+ }{\text{} }^{6} \mathrm{Li} $. For the conditions of complete vertical outer ionization (CVI) of the nanodroplet[Reference Heidenreich, Last and Jortner2,Reference Last and Jortner22–Reference Last and Jortner24] , the CE energetics is determined by electrostatic models[Reference Heidenreich, Last and Jortner2,Reference Last and Jortner22,Reference Heidenreich, Last, Jortner, Kühn and Wöste23] . Under CVI conditions the kinetic energy distribution of the deuterons is[Reference Heidenreich, Last and Jortner2,Reference Last and Jortner22,Reference Heidenreich, Last, Jortner, Kühn and Wöste23]
$\mathrm{D} {+ }{\text{} }^{6} \mathrm{Li} $. For the conditions of complete vertical outer ionization (CVI) of the nanodroplet[Reference Heidenreich, Last and Jortner2,Reference Last and Jortner22–Reference Last and Jortner24] , the CE energetics is determined by electrostatic models[Reference Heidenreich, Last and Jortner2,Reference Last and Jortner22,Reference Heidenreich, Last, Jortner, Kühn and Wöste23] . Under CVI conditions the kinetic energy distribution of the deuterons is[Reference Heidenreich, Last and Jortner2,Reference Last and Jortner22,Reference Heidenreich, Last, Jortner, Kühn and Wöste23] ![]() $P(E)= (3/ 2{E}_{\max } )\mathop{(E/ {E}_{\max } )}\nolimits ^{1/ 2} $ for
$P(E)= (3/ 2{E}_{\max } )\mathop{(E/ {E}_{\max } )}\nolimits ^{1/ 2} $ for ![]() $0\lt E\leq {E}_{\max } $, with the maximal kinetic energy being[Reference Heidenreich, Last and Jortner2,29,Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30]
$0\lt E\leq {E}_{\max } $, with the maximal kinetic energy being[Reference Heidenreich, Last and Jortner2,29,Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30] ![]() ${E}_{\max } = a{ R}_{0}^{2} $, where
${E}_{\max } = a{ R}_{0}^{2} $, where ![]() $a= (4\pi / 3)\bar {B} {\rho }_{\mathrm{mol} } {q}^{2} $, with
$a= (4\pi / 3)\bar {B} {\rho }_{\mathrm{mol} } {q}^{2} $, with ![]() $\bar {B} = 1. 44\times 1{0}^{- 3} ~\mathrm{keV} ~\mathrm{nm} $,
$\bar {B} = 1. 44\times 1{0}^{- 3} ~\mathrm{keV} ~\mathrm{nm} $, ![]() ${\rho }_{\mathrm{mol} } $ is the initial density of the nanostructure, and
${\rho }_{\mathrm{mol} } $ is the initial density of the nanostructure, and ![]() $q= 1$ is the ion charge. The validity of the CVI relations for the energetics of CE is borne out of SEID simulations[Reference Last and Jortner24,Reference Ron, Last and Jortner26,Reference Last and Jortner34,Reference Last and Jortner35] , which include intra-nanodroplet intensity attenuation[Reference Last and Jortner24] and relativistic effects[Reference Last and Jortner37,Reference Last and Jortner38] . Equations (1), (2) and (4), together with the CVI relations for
$q= 1$ is the ion charge. The validity of the CVI relations for the energetics of CE is borne out of SEID simulations[Reference Last and Jortner24,Reference Ron, Last and Jortner26,Reference Last and Jortner34,Reference Last and Jortner35] , which include intra-nanodroplet intensity attenuation[Reference Last and Jortner24] and relativistic effects[Reference Last and Jortner37,Reference Last and Jortner38] . Equations (1), (2) and (4), together with the CVI relations for ![]() ${E}_{\max } $ and
${E}_{\max } $ and ![]() $P(E)$, result in
$P(E)$, result in
with
Equation (5) predicts a power law for the nanodroplet size dependence of the fusion yields, with the scaling parameter ![]() $\zeta $ being given by Equation (6).
$\zeta $ being given by Equation (6).

Figure 1. Nanodroplet size dependence of the table-top fusion yields ![]() $Y$, Equation (1), within the source–target design for the fusion of deuterons with a solid hollow cylinder of
$Y$, Equation (1), within the source–target design for the fusion of deuterons with a solid hollow cylinder of ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, solid deuterium, and deuterated polyethylene
${}^{6} \mathrm{Li} $, solid deuterium, and deuterated polyethylene ![]() $({\mathrm{CD} }_{2} )$, as marked on the curves. The laser parameters are
$({\mathrm{CD} }_{2} )$, as marked on the curves. The laser parameters are ![]() ${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $,
${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, ![]() $\tau = 30~\mathrm{fs} $, and
$\tau = 30~\mathrm{fs} $, and ![]() $\boldsymbol{W}= 0. 6~\mathrm{J} $. The inset shows the energy dependence of the fusion reaction probability
$\boldsymbol{W}= 0. 6~\mathrm{J} $. The inset shows the energy dependence of the fusion reaction probability ![]() $y(E)$.
$y(E)$.
The fusion yields, Equation (1), were calculated from
(i) the
 $y(E)$ data of Equation (3) (presented in the inset to Figure 1), and the
$y(E)$ data of Equation (3) (presented in the inset to Figure 1), and the  $P(E)$ functions obtained from SEID simulations, which result in
$P(E)$ functions obtained from SEID simulations, which result in  $\langle y\rangle $, Equation (2);
$\langle y\rangle $, Equation (2);(ii) the number
 $N$ of the deuterons produced from the Coulomb-exploding source.
$N$ of the deuterons produced from the Coulomb-exploding source.
![]() $N$ is governed by laser energy deposition inside the plasma filament within the laser focal volume[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] . The fraction
$N$ is governed by laser energy deposition inside the plasma filament within the laser focal volume[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] . The fraction ![]() $\beta $ of the laser energy acquisition by the assembly of nanodroplets is[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26]
$\beta $ of the laser energy acquisition by the assembly of nanodroplets is[Reference Last, Ron and Jortner25,Reference Ron, Last and Jortner26] ![]() $\beta = N{E}_{\mathrm{abs} } / \boldsymbol{W}$ with
$\beta = N{E}_{\mathrm{abs} } / \boldsymbol{W}$ with ![]() $0\leq \beta \leq 1$, where
$0\leq \beta \leq 1$, where ![]() $\boldsymbol{W}$ is the laser pulse energy and
$\boldsymbol{W}$ is the laser pulse energy and ![]() ${E}_{\mathrm{abs} } $ is the laser energy absorbed per atom within a nanodroplet, which was obtained from SEID simulations for exploding deuterium nanodroplets, while the laser parameters are the peak intensity
${E}_{\mathrm{abs} } $ is the laser energy absorbed per atom within a nanodroplet, which was obtained from SEID simulations for exploding deuterium nanodroplets, while the laser parameters are the peak intensity ![]() ${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, pulse duration
${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, pulse duration ![]() $\tau = 3\times 1{0}^{- 14} ~\mathrm{s} $, pulse energy
$\tau = 3\times 1{0}^{- 14} ~\mathrm{s} $, pulse energy ![]() $\boldsymbol{W}= 0. 6~\mathrm{J} $[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17], and laser wavelength
$\boldsymbol{W}= 0. 6~\mathrm{J} $[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17], and laser wavelength ![]() $\lambda = 8\times 1{0}^{- 5} ~\mathrm{cm} $. Following our previous work[Reference Ron, Last and Jortner26], the number of deuterons within the macroscopic plasma filament is
$\lambda = 8\times 1{0}^{- 5} ~\mathrm{cm} $. Following our previous work[Reference Ron, Last and Jortner26], the number of deuterons within the macroscopic plasma filament is
for the weak assembly intensity attenuation, and
for the strong assembly intensity attenuation. Here, the macroscopic plasma filament is characterized by the deuteron density, where ![]() $\rho = 3\times 1{0}^{18} ~{\mathrm{cm} }^{- 3} $[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17].
$\rho = 3\times 1{0}^{18} ~{\mathrm{cm} }^{- 3} $[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17].
The nanodroplet size dependence of the fusion yields was calculated for the laser and nanoplasma parameters given above. For these input data, the weak assembly attenuation limit ![]() $\beta \lt 1$ is strictly applicable over the entire size domain[Reference Ron, Last and Jortner26]. Furthermore, for the highest laser intensity
$\beta \lt 1$ is strictly applicable over the entire size domain[Reference Ron, Last and Jortner26]. Furthermore, for the highest laser intensity ![]() ${I}_{M} = 5\times 1{0}^{19} $, the CVI relation is nearly applicable up to
${I}_{M} = 5\times 1{0}^{19} $, the CVI relation is nearly applicable up to ![]() ${R}_{0} = 300~\mathrm{nm} $, whereupon Equation (5) is applicable for the analysis of the yield data. The nanodroplet size dependence of
${R}_{0} = 300~\mathrm{nm} $, whereupon Equation (5) is applicable for the analysis of the yield data. The nanodroplet size dependence of ![]() $Y$ portrayed in Figure 1 exhibits a nearly linear dependence of log
$Y$ portrayed in Figure 1 exhibits a nearly linear dependence of log ![]() $Y$ versus
$Y$ versus ![]() $\log {R}_{0} $, resulting in a power-law size dependence of
$\log {R}_{0} $, resulting in a power-law size dependence of ![]() $Y$ on
$Y$ on ![]() ${R}_{0} $, of the form
${R}_{0} $, of the form ![]() $Y\propto { R}_{0}^{\varsigma } $. The scaling parameters
$Y\propto { R}_{0}^{\varsigma } $. The scaling parameters ![]() $\zeta $ obtained for Figure 1 are
$\zeta $ obtained for Figure 1 are ![]() $\zeta = 3. 3\pm 0. 5$ for
$\zeta = 3. 3\pm 0. 5$ for ![]() $\mathrm{D} {+ }\mathrm{D} $,
$\mathrm{D} {+ }\mathrm{D} $, ![]() $\zeta = 4. 5\pm 0. 7$ for
$\zeta = 4. 5\pm 0. 7$ for ![]() $\mathrm{D} {+ }{\text{} }^{7} \mathrm{Li} $, and
$\mathrm{D} {+ }{\text{} }^{7} \mathrm{Li} $, and ![]() $\zeta = 5. 4\pm 0. 6$ for
$\zeta = 5. 4\pm 0. 6$ for ![]() $\mathrm{D} {+ }{\text{} }^{6} \mathrm{Li} $. These scaling parameters
$\mathrm{D} {+ }{\text{} }^{6} \mathrm{Li} $. These scaling parameters ![]() $\zeta $, obtained for the nanodroplet size dependence of
$\zeta $, obtained for the nanodroplet size dependence of ![]() $Y$, obey the relation
$Y$, obey the relation ![]() $\zeta = 2\xi $, where
$\zeta = 2\xi $, where ![]() $\xi $, Equation (4), are the scaling parameters for the energy dependence reaction probability, Equation (3), which are presented above. This result is in accord with the relation predicted by Equation (6).
$\xi $, Equation (4), are the scaling parameters for the energy dependence reaction probability, Equation (3), which are presented above. This result is in accord with the relation predicted by Equation (6).
4. Fusion efficiencies and their dependence on the laser pulse energy
The fusion efficiency[Reference Li, Liu, Ni, Li and Xu15,Reference Ron, Last and Jortner26,Reference Davis and Petrov39] is
The fusion yields and efficiencies were maximized for the nanodroplet size and the laser parameters. Our results for ![]() $Y$ (Figure 1) and
$Y$ (Figure 1) and ![]() $\Phi $ were obtained at a fixed laser pulse energy of
$\Phi $ were obtained at a fixed laser pulse energy of ![]() ${\boldsymbol{W}}_{0} = 0. 6~\mathrm{J} $[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17] and at a high laser intensity of
${\boldsymbol{W}}_{0} = 0. 6~\mathrm{J} $[Reference Ter-Avetisyan, Schnürer, Hilscher, Jahnke, Busch, Nicles and Sandner17] and at a high laser intensity of ![]() ${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $. We shall now advance a scaling method for the dependence of
${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $. We shall now advance a scaling method for the dependence of ![]() $Y$ and
$Y$ and ![]() $\Phi $ on the laser pulse energy
$\Phi $ on the laser pulse energy ![]() $\boldsymbol{W}$ for the domains of weak assembly intensity attenuation (
$\boldsymbol{W}$ for the domains of weak assembly intensity attenuation (![]() $\beta \lt 1$) and strong assembly intensity attenuation (
$\beta \lt 1$) and strong assembly intensity attenuation (![]() $\beta = 1$). Increasing
$\beta = 1$). Increasing ![]() $\boldsymbol{W}$ beyond
$\boldsymbol{W}$ beyond ![]() ${\boldsymbol{W}}_{0} $ is expected to increase
${\boldsymbol{W}}_{0} $ is expected to increase ![]() $Y$ and
$Y$ and ![]() $\Phi $ for
$\Phi $ for ![]() $\beta \lt 1$ in the range
$\beta \lt 1$ in the range ![]() ${\boldsymbol{W}}_{0} \lt \boldsymbol{W}\leq {\boldsymbol{W}}_{M} $, while for
${\boldsymbol{W}}_{0} \lt \boldsymbol{W}\leq {\boldsymbol{W}}_{M} $, while for ![]() $\beta = 1$ a distinct dependence of the parameters on
$\beta = 1$ a distinct dependence of the parameters on ![]() $\boldsymbol{W}$ is realized in the range
$\boldsymbol{W}$ is realized in the range ![]() $\boldsymbol{W}\gt {\boldsymbol{W}}_{M} $.
$\boldsymbol{W}\gt {\boldsymbol{W}}_{M} $. ![]() ${\boldsymbol{W}}_{M} $ marks the laser power for the ‘transition’ from
${\boldsymbol{W}}_{M} $ marks the laser power for the ‘transition’ from ![]() $\beta \lt 1$ to
$\beta \lt 1$ to ![]() $\beta = 1$, which is given by[Reference Ron, Last and Jortner26]
$\beta = 1$, which is given by[Reference Ron, Last and Jortner26]
A typical value of ![]() ${\boldsymbol{W}}_{M} = 8~\mathrm{J} $ for the largest nanodroplet size and highest intensity, i.e.,
${\boldsymbol{W}}_{M} = 8~\mathrm{J} $ for the largest nanodroplet size and highest intensity, i.e., ![]() ${R}_{0} = 300~\mathrm{nm} $ and
${R}_{0} = 300~\mathrm{nm} $ and ![]() ${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, was estimated from Equation (9). The
${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $, was estimated from Equation (9). The ![]() $\boldsymbol{W}$ scaling of
$\boldsymbol{W}$ scaling of ![]() $Y(\boldsymbol{W})$ and of
$Y(\boldsymbol{W})$ and of ![]() $\Phi (\boldsymbol{W})$ is obtained in the form[Reference Ron, Last and Jortner26]
$\Phi (\boldsymbol{W})$ is obtained in the form[Reference Ron, Last and Jortner26]
and
Accordingly, the calculation of the maximal value of ![]() $\Phi $ will be achieved by SEID simulations for the optimization of
$\Phi $ will be achieved by SEID simulations for the optimization of ![]() $Y$ and
$Y$ and ![]() $\Phi $ at a fixed laser pulse energy (
$\Phi $ at a fixed laser pulse energy (![]() ${\boldsymbol{W}}_{0} \lt {\boldsymbol{W}}_{M} $), followed by the
${\boldsymbol{W}}_{0} \lt {\boldsymbol{W}}_{M} $), followed by the ![]() $\boldsymbol{W}$ scaling of these attributes from
$\boldsymbol{W}$ scaling of these attributes from ![]() ${\boldsymbol{W}}_{0} $ to
${\boldsymbol{W}}_{0} $ to ![]() ${\boldsymbol{W}}_{M} $. The maximal value of
${\boldsymbol{W}}_{M} $. The maximal value of ![]() $\Phi $ is
$\Phi $ is ![]() $\Phi ({\boldsymbol{W}}_{M} )$. Our results for
$\Phi ({\boldsymbol{W}}_{M} )$. Our results for ![]() $Y({\boldsymbol{W}}_{M} )$ and
$Y({\boldsymbol{W}}_{M} )$ and ![]() $\Phi ({\boldsymbol{W}}_{M} )$ were obtained from the scaling of the SEID simulation results at
$\Phi ({\boldsymbol{W}}_{M} )$ were obtained from the scaling of the SEID simulation results at ![]() ${\boldsymbol{W}}_{0} = 0. 6~\mathrm{J} $ (Figure 2). The optimal fusion yields per laser pulse (for the nanodroplet size
${\boldsymbol{W}}_{0} = 0. 6~\mathrm{J} $ (Figure 2). The optimal fusion yields per laser pulse (for the nanodroplet size ![]() ${R}_{0} = 300~\mathrm{nm} $, and laser parameters
${R}_{0} = 300~\mathrm{nm} $, and laser parameters ![]() ${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 1} $,
${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 1} $, ![]() $\tau = 30~\mathrm{fs} $, and
$\tau = 30~\mathrm{fs} $, and ![]() ${\boldsymbol{W}}_{M} = 8~\mathrm{J} $) are
${\boldsymbol{W}}_{M} = 8~\mathrm{J} $) are ![]() $Y({\boldsymbol{W}}_{M} )= 3. 4\times 1{0}^{10} $,
$Y({\boldsymbol{W}}_{M} )= 3. 4\times 1{0}^{10} $, ![]() $1. 7\times 1{0}^{10} $, and
$1. 7\times 1{0}^{10} $, and ![]() $5. 3\times 1{0}^{9} $ for the fusion of D with
$5. 3\times 1{0}^{9} $ for the fusion of D with ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, and D, respectively. Our analysis then results in the attainment of the maximal high table-top fusion efficiencies, i.e.,
${}^{6} \mathrm{Li} $, and D, respectively. Our analysis then results in the attainment of the maximal high table-top fusion efficiencies, i.e., ![]() $\Phi ({\boldsymbol{W}}_{M} )= 4\times 1{0}^{9} ~{\mathrm{J} }^{- 1} , 2\times 1{0}^{9} ~{\mathrm{J} }^{- 1} $, and
$\Phi ({\boldsymbol{W}}_{M} )= 4\times 1{0}^{9} ~{\mathrm{J} }^{- 1} , 2\times 1{0}^{9} ~{\mathrm{J} }^{- 1} $, and ![]() $7\times 1{0}^{8} ~{\mathrm{J} }^{- 1} $ for the fusion of D with
$7\times 1{0}^{8} ~{\mathrm{J} }^{- 1} $ for the fusion of D with ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, and D, respectively.
${}^{6} \mathrm{Li} $, and D, respectively.

Figure 2. A record of the currently available data for the dependence of the efficiency ![]() $\Psi $ of conversion of laser energy to nuclear energy on the laser pulse energy
$\Psi $ of conversion of laser energy to nuclear energy on the laser pulse energy ![]() $\boldsymbol{W}$ for table-top fusion driven by CE of nanodroplets and in a source–target design. A comparison is presented between experimental data for DD fusion driven by CE of (
$\boldsymbol{W}$ for table-top fusion driven by CE of nanodroplets and in a source–target design. A comparison is presented between experimental data for DD fusion driven by CE of (![]() ${\mathrm{D} }_{2} {\mathop{)}\nolimits}_{n} $ and
${\mathrm{D} }_{2} {\mathop{)}\nolimits}_{n} $ and ![]() $\mathop{({\mathrm{CD} }_{4} )}\nolimits_{n} $ clusters inside and outside a macroscopic plasma filament[Reference Grillon, Balcou, Chambaret, Hulin, Martino, Moustaizis, Notebaert, Pittman, Pussieux, Rousse, Rousseau, Sebban, Sublemontier and Schmidt5–Reference Lu, Liu, Wang, Wang, Zhou, Deng, Xia, Xu, Lu, Jiang, Leng, Liang, Ni, Li and Xu8], theoretical–computational data for fusion of deuterium with light atoms
$\mathop{({\mathrm{CD} }_{4} )}\nolimits_{n} $ clusters inside and outside a macroscopic plasma filament[Reference Grillon, Balcou, Chambaret, Hulin, Martino, Moustaizis, Notebaert, Pittman, Pussieux, Rousse, Rousseau, Sebban, Sublemontier and Schmidt5–Reference Lu, Liu, Wang, Wang, Zhou, Deng, Xia, Xu, Lu, Jiang, Leng, Liang, Ni, Li and Xu8], theoretical–computational data for fusion of deuterium with light atoms ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, T, and D within the source–target design (present work and reference 26), and of experimental data for DT and DD inertial fusion in ‘big science’ inertial fusion setups [Reference Cok, Craxton and McKenty28–Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30].
${}^{6} \mathrm{Li} $, T, and D within the source–target design (present work and reference 26), and of experimental data for DT and DD inertial fusion in ‘big science’ inertial fusion setups [Reference Cok, Craxton and McKenty28–Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30].
The maximal value of the laser energy to nuclear energy conversion efficiency for table-top fusion is
where ![]() $Q$ is the energy release in the nuclear reaction and
$Q$ is the energy release in the nuclear reaction and ![]() $\Phi ({\boldsymbol{W}}_{M} )= Y({\boldsymbol{W}}_{M} )/ {\boldsymbol{W}}_{M} $. The estimates for
$\Phi ({\boldsymbol{W}}_{M} )= Y({\boldsymbol{W}}_{M} )/ {\boldsymbol{W}}_{M} $. The estimates for ![]() $\Psi ({\boldsymbol{W}}_{M} )$ for the fusion of D with
$\Psi ({\boldsymbol{W}}_{M} )$ for the fusion of D with ![]() ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $, ![]() ${}^{6} \mathrm{Li} $, and D are
${}^{6} \mathrm{Li} $, and D are ![]() $1. 0\times 1{0}^{- 2} , 1. 1\times 1{0}^{- 3} $, and
$1. 0\times 1{0}^{- 2} , 1. 1\times 1{0}^{- 3} $, and ![]() $3. 9\times 1{0}^{- 4} $, respectively.
$3. 9\times 1{0}^{- 4} $, respectively.
5. Discussion
Of considerable interest is the attainment of high efficiencies for the conversion of laser energy to nuclear energy. Two major conclusions regarding records for table-top fusion emerge from our analysis.
(1) Records for table-top conversion of laser energy to nuclear energy. Our theoretical–computational studies demonstrate the attainment of high fusion efficiencies in the range
 $\Phi ({\boldsymbol{W}}_{M} )\simeq 1{0}^{9} ~{\mathrm{J} }^{- 1} $ for the fusion reaction of D with
$\Phi ({\boldsymbol{W}}_{M} )\simeq 1{0}^{9} ~{\mathrm{J} }^{- 1} $ for the fusion reaction of D with  ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $,  ${}^{6} \mathrm{Li} $, and D. These data constitute the highest table-top fusion yields and efficiencies obtained to date. The source–target design, constituting of an exploding nanodroplets source driven by a superintense laser and a solid hollow cylinder target, provides the most efficient device for the table-top conversion of laser energy to nuclear energy.
${}^{6} \mathrm{Li} $, and D. These data constitute the highest table-top fusion yields and efficiencies obtained to date. The source–target design, constituting of an exploding nanodroplets source driven by a superintense laser and a solid hollow cylinder target, provides the most efficient device for the table-top conversion of laser energy to nuclear energy.(2) Table-top laser
 $\rightarrow $ nuclear conversion efficiency is comparable to that in giant fusion machines attained to date. The table-top laser energy
$\rightarrow $ nuclear conversion efficiency is comparable to that in giant fusion machines attained to date. The table-top laser energy  $\rightarrow $ nuclear energy conversion efficiency within the source–target design is comparable to that obtained to date in the ‘big science’ setups for inertial fusion[Reference Dittrich, Hammel, Keane, McEachren, Tuner, Haan and Suter27–Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30]. This is evident from the currently available data (Figure 2), where the table-top ‘big science’ fusion
$\rightarrow $ nuclear energy conversion efficiency within the source–target design is comparable to that obtained to date in the ‘big science’ setups for inertial fusion[Reference Dittrich, Hammel, Keane, McEachren, Tuner, Haan and Suter27–Reference Yu-dong, Tian-Xuan, Huang, Xia-Yu, Xiao-Shi, Tang-Qi, Zi-Feng, Jia-Bin, Tian-Ming, Ming, Rui-Zhen, Xiao-An, Chao-Guang, Lu, Jia-Hua, Long-Fei, Bo-Lun, Ming, Wei, Bo, Ji, Ping, Hai-Le, Shao-En and Yong-Kun30]. This is evident from the currently available data (Figure 2), where the table-top ‘big science’ fusion  $\Psi $ data fall into two domains characterized by different laser pulse powers: (i) the lower pulse power range (
$\Psi $ data fall into two domains characterized by different laser pulse powers: (i) the lower pulse power range ( $\boldsymbol{W}= 0. 1{\unicode{x2013}} 10~\mathrm{J} $) for table-top cluster NFDCE and for the source–target design; and (ii) the high pulse power range (
$\boldsymbol{W}= 0. 1{\unicode{x2013}} 10~\mathrm{J} $) for table-top cluster NFDCE and for the source–target design; and (ii) the high pulse power range ( $\boldsymbol{W}= 6\times 1{0}^{3} {\unicode{x2013}} 3\times 1{0}^{6} ~\mathrm{J} $) for ‘big science’ inertial fusion. From the outline portrayed in Figure 2, we infer that high values of
$\boldsymbol{W}= 6\times 1{0}^{3} {\unicode{x2013}} 3\times 1{0}^{6} ~\mathrm{J} $) for ‘big science’ inertial fusion. From the outline portrayed in Figure 2, we infer that high values of  $\Psi ({\boldsymbol{W}}_{M} )$, in the range
$\Psi ({\boldsymbol{W}}_{M} )$, in the range  $1{0}^{- 2} $–
$1{0}^{- 2} $– $1{0}^{- 3} $, can be attained for the fusion of D with
$1{0}^{- 3} $, can be attained for the fusion of D with  ${}^{7} \mathrm{Li} $,
${}^{7} \mathrm{Li} $,  ${}^{6} \mathrm{Li} $, and D (Section 4), and with T[Reference Ron, Last and Jortner26] within the table-top source–target design with a source of Coulomb-exploding large deuterium nanodroplets (
${}^{6} \mathrm{Li} $, and D (Section 4), and with T[Reference Ron, Last and Jortner26] within the table-top source–target design with a source of Coulomb-exploding large deuterium nanodroplets ( ${R}_{0} = 300~\mathrm{nm} $) driven by a superintense laser (
${R}_{0} = 300~\mathrm{nm} $) driven by a superintense laser ( ${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ and
${I}_{M} = 5\times 1{0}^{19} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ and  ${\boldsymbol{W}}_{M} = 8~\mathrm{J} $). These high
${\boldsymbol{W}}_{M} = 8~\mathrm{J} $). These high  $\Psi ({\boldsymbol{W}}_{M} )$ results for the table-top source–target design fall within
$\Psi ({\boldsymbol{W}}_{M} )$ results for the table-top source–target design fall within  ${\sim }1$ order of magnitude in comparison with those obtained for DT fusion in ‘big science’ setups, i.e., in the OMEGA laser system (
${\sim }1$ order of magnitude in comparison with those obtained for DT fusion in ‘big science’ setups, i.e., in the OMEGA laser system ( $\boldsymbol{W}= 30~\mathrm{kJ} , Y= 1{0}^{14} $,
$\boldsymbol{W}= 30~\mathrm{kJ} , Y= 1{0}^{14} $,  $\Phi = 3\times 1{0}^{9} ~{\mathrm{J} }^{- 1} $, and
$\Phi = 3\times 1{0}^{9} ~{\mathrm{J} }^{- 1} $, and  $\Psi = 1. 2\times 1{0}^{- 2} $[Reference Cok, Craxton and McKenty28]) and in the National Ignition Facility (NIF) system (
$\Psi = 1. 2\times 1{0}^{- 2} $[Reference Cok, Craxton and McKenty28]) and in the National Ignition Facility (NIF) system ( $\boldsymbol{W}= 1. 43~\mathrm{MJ} , Y= 6\times 1{0}^{14} $,
$\boldsymbol{W}= 1. 43~\mathrm{MJ} , Y= 6\times 1{0}^{14} $,  $\Phi = 4. 1\times 1{0}^{8} $, and
$\Phi = 4. 1\times 1{0}^{8} $, and  $\Psi = 1. 3\times 1{0}^{- 3} $[29]).
$\Psi = 1. 3\times 1{0}^{- 3} $[29]).
Acknowledgements
This research was supported by the Binational German–Israeli James Franck Program on laser–matter interaction at Tel-Aviv University and by the Spanish Ministry of Science and Education (MICINN) and by the SAIOTEK Program of the Basque government at the University of the Basque Country.