3.1. IW measurement

Aggregated capital is a term for inclusive investment, a key indicator of IW. According to Arrow et al. (Reference Arrow, Dasgupta and Mäler2003), an economy enjoys sustainable development if and only if its IW is at a constant price or does not decline relative to its population. IW is a measure of intergenerational well-being, where the accumulation of wealth corresponds to sustained development and is a key to economic progress (Dasgupta, Reference Dasgupta2007). Thus, we can define IW at the time t as W_t, which includes produced, human and natural capital. This can be defined as:

$$W\lpar t \rpar = Q\lpar t \rpar t + \;\mathop\sum\nolimits_{i} P_{i\;}\lpar t \rpar \;K_{i\;}\lpar t \rpar = P_{PC}PC\lpar t \rpar + \;P_{HC}HC\lpar t \rpar + P_{NC}NC\lpar t \rpar \comma \;$$

where Q(t) is the shadow price of the time asset (TFP in our case). Each P is a shadow price of the capital asset, defined as δW_t/δC, where K is each capital, which is PC(t), HC(t) and NC(t) representing produced capital, human capital and natural capital at time t, respectively. Therefore, the total capital asset comprises the resource base that is calculated by using the marginal contribution of each asset type to social welfare, which is represented by the social (or shadow) price of all of the assets under evaluation. This present value is called an asset's shadow price. Hence, an economy's IW is the shadow value of its productive base, and inclusive investment, IW(t), is the shadow value of the net change in its productive base (Dasgupta, Reference Dasgupta2008). All capitals are evaluated on the basis of each of their own accounting prices in the current period. The IW should always be positive in order to be sustainable in the future, or at least not decline over a period of time; thus, the sustainability condition can be expressed as:

$$IW\lpar t \rpar \ge 0\; {\rm for\ all}\,t\lpar {{\rm time}} \rpar . $$

3.2. TFP measurement

To measure cross-country productivity, we adopt the MPI as described by Coelli et al. (Reference Coelli, Rao and Battese1998) and Färe et al. (Reference Färe, Grosskopf, Norris and Zhongyang1994) as a measurement of TFP in order to investigate whether there is any change in wealth when mapping capital assets (human capital, produced capital and natural capital). This is because the MPI is suitable for assessing the relationship between inputs and outputs under the multivariate input inefficiency. By using the MPI, technological progress and the inefficiency of resource use can also be estimated. Therefore, the MPI can be considered as the most suitable index for achieving the objectives of this research.

When calculating TFP, we applied produced, human and natural capital as a separate unit, with each capital as an input and GDP as an output. Because of the multivariate inputs (produced, human and natural capital), we adopted the non-parametric frontier analysis of DEA in order to measure TFP. By using the distance function specification, our problem can be formulated as follows:

(1)$$T\lpar t \rpar \equiv \lcub {\lpar {x_t\comma \;y_t} \rpar \colon\; x_t\;can\;produce\;y_t} \rcub .$$

In this case, $x = \lpar {x^1\comma \;\ldots x^M} \rpar \in R_ + ^M $ and $y = \lpar {y^1\comma \;\ldots y^N} \rpar \in R_ + ^N $ are the input and output vectors, respectively. The technology set is defined by Eq. (2), which consists of all feasible input vectors, x_t, and output vectors, y_t, at time t. According to Managi (Reference Managi2011), the estimation of efficiency relative to the production frontiers relies on the theory of distance or gauge functions. In economics, distance functions are related to the notion of the coefficient of resource utilization (Debreu, Reference Debreu1951) and to efficiency measures (Farrell, Reference Farrell1957). This distance function defined t as:

(2)$$d^t\lpar {y_t\comma \;x_t} \rpar = min\lcub {\delta\; \colon \lpar {x_t\comma \;y_t/\delta } \rpar \in T\lpar t \rpar } \rcub \comma \;$$

where δ is the maximal proportional amount to which y _t can be expanded given technology T(t). DEA and the output-orientated function are used in order to estimate the distance function under constant returns to scale by solving the following optimization problem (Managi, Reference Managi2003):

$$d_{T\lpar t \rpar }\lpar {x_t\comma \;y_t} \rpar = max_{\delta \comma \lambda }\delta $$

$$s.t\;Y_t\lambda \ge \displaystyle{{y_i^t } \over \delta }$$

$$X_t\lambda \le x_i^t $$

(3)$$\lambda \ge 0.$$

From Eq. (3), δ is the measure of efficiency for country i in year t, λ is an N × 1 vector of weights and Y _t and inputs X _t are the vectors of outputs y _t and inputs x _t. In order to estimate productivity over time, several distance functions are used for the input–output vector for period t + 1 and technology in period t. The MPI (M ₀) for the output-orientated productivity index is as follows:

(4)$$M_0\lpar {y_t\comma \;x_t\comma \;y_{t + 1}\comma \;x_{t + 1}} \rpar = \;\left[{\displaystyle{{d_o^t \lpar {y_{t + 1\comma \;}x_{t + 1}} \rpar } \over {d_o^t \lpar {y_t\comma \;x_t} \rpar }}\;\times \;\displaystyle{{d_o^{t + 1} \lpar {y_{t + 1\comma }x_{t + 1}} \rpar } \over {d_o^{t + 1} \lpar {y_t\comma \;x_t} \rpar }}} \right]^{{1 \over 2}}.$$

In Eq. (4), d represents the geometric distance to the frontier, which can be decomposed into efficiency change (i.e., catching up to the frontier) and technological change (i.e., change in the production frontier) (Färe et al., Reference Färe, Grosskopf, Norris and Zhongyang1994). Based on this formula, a country on the frontier will perform better under the same resource constraints than a country that is further away from the frontier. The estimation of this is performed by using DEA, which is a non-parametric estimation method. M ₀ can be divided into two components: efficiency change represents the first ratio, while technological change represents the second. Based on this formulation, we estimate the MPI and estimated IW as follows:

(5)$$f\colon \lcub {\;P_{PC}PC\comma \;\;P_{HC}HC\comma \;\;P_{NC}NC} \rcub \;\,IW.$$

In this estimation, it is possible for two countries to have different levels of sustainable development, even if they have similar levels of capital assets. This is due to the fact that sustainable development is dependent not only on how the countries use their capital assets, but also on their different saving rates. The MPI is reformulated as follows:

$$M_0\lpar {GDP_{i\comma t}\comma \;PC_{i\comma t}\comma \;HC_{i\comma t}\comma \;NC_{i\comma t}\comma \;GDP_{i\comma t + 1}\comma \;PC_{i\comma t + 1}\comma \;HC_{i\comma \;t + 1}\comma \;NC_{i\comma t + 1}} \rpar .$$

(6)$$\eqalign{&= \left[{\displaystyle{{d^t\lpar {GDP_{i\comma t}\comma \;PC_{i\comma t + 1}\comma \;HC_{i\comma t + 1}\comma \;NC_{i\comma t + 1}} \rpar } \over {d^t\lpar {GDP_{i\comma t}\comma \;PC_{i\comma t}\comma \;HC_{i\comma t}\comma \;NC_{i\comma t}} \rpar }}\;}\right\cr& \left{\times \;\displaystyle{{d^{t + 1}\lpar {GDP_{i\comma t + 1}\comma \;PC_{i\comma t + 1}\comma \;HC_{i\comma t + 1}\comma \;NC_{i\comma t + 1}} \rpar } \over {d^{t + 1}\lpar {GDP_{i\comma t}\comma \;PC_{i\comma t}\comma \;HC_{i\comma t}\comma \;NC_{i\comma t}} \rpar }}} \right]^{{1 \over 2}}.}$$

Eq. (6) indicates the feasibility of producing goods with fewer inputs. Where d is the geometric distance to the production frontier, it represents the best available technology for the given inputs and output. The country under analysis in this research refers to i, which runs from 1 to 140 countries in our sample. This index is measured by the ratio between 2 years; thus, a value greater than 1 represents an improvement or otherwise in the TFP calculation. Using this index allows us to examine TFP's contribution to IW by country.

3.3. IW adjusted by TFP measurement

By using the new TFP results and based on the IW methodology, we estimated each country's IW-TFP Adjusted for the years 1990–2010. We did so by using the annual average of IW per capita and estimated the percentage change of TFP on the IW as the sustainability indicator. In order to estimate the IW-TFP Adjusted, we calculated the growth rate of IW per capita. We also followed the same process as Arrow et al. (Reference Arrow, Dasgupta, Goulder, Daily, Ehrlich, Heal and Walker2004) with the compromise of the use of TFP growth from Collins and Bosworth (Reference Collins and Bosworth1996), which was based on GDP output. According to the framework of sustainable development, the IW-TFP Adjusted should be maintained at a positive and non-declining state. The calculation is as follows:

$$IW-TFP\;Adjusted = IW + TFP \comma \;$$

where IW-TFP Adjusted is the inclusive wealth adjusted with total factor productivity, IW is the inclusive wealth growth per capita and TFP is the total factor productivity growth.

Based on the TFP results from 1990 to 2010, we measured not only IWI-TFP Adjusted, but also how countries’ performance affected IW after three main factors were taken into consideration. Those three factors are as follows: (1) climate change, particularly the damage suffered as a result of increased atmospheric carbon; (2) TFP's contribution to multiple factors missing from economic growth; and (3) oil capital gains related to the change in oil prices, which may either increase or decrease a country's productivity value.

Based on the 2012 and 2014 Inclusive Wealth Reports (UNU-IHDP & UNEP, 2012, 2014), we refer to this adjusted figure as the Inclusive Wealth Index Adjusted (IWI Adjusted). We measured the change in wealth for 140 countries over 21 years on a per capita basis. In order to estimate the change in wealth, we calculated the average annual growth rates in wealth and population. According to the framework of sustainable development, the IWI Adjusted should remain positive and non-declining. The calculation is as follows:

$$IWI\;Adjusted = IW + C + E + TFP\comma \;$$

where IWI Adjusted is the Inclusive Wealth Index Adjusted, IW is the inclusive wealth per capita, C is the carbon damage, E is the energy depletion (i.e., oil capital gain) and TFP is the percentage of TFP growth.

Based on the adjustment set forth above, the IWI Adjusted can have either a positive or a negative effect on countries’ IW. According to Nordhaus and Boyer (Reference Nordhaus and Boyer2000), climate change will benefit some countries, whereas others will experience a negative impact. In terms of oil price fluctuations, normally countries that are considered as oil producers will realize the advantages and positive changes in wealth compared to countries that depend on oil imports.

3.4. Data

For the sources of these data, we refer to the 2014 Inclusive Wealth Report published by UNU-IHDP and UNEP (2014). This dataset provides quantitative information on data for 140 countries from 1990 to 2010. As noted above, the accounting shadow balance sheet included as inputs here consists not only of produced capital and human capital, but also natural capital. To measure natural capital wealth, fossil fuels (oil, coal and natural gas), minerals (nickel, gold, silver, iron, lead, tin, zinc, phosphate, copper and bauxite), forest resources (timber and non-timber) and agricultural land (cropland and pastureland) are used. For human capital wealth, the calculation uses education attainment and the additional compensation over time as developed by Arrow et al. (Reference Arrow, Goulder, Mumford and Oleson2012). The BP Statistical Review of World Energy (BP, 2013) is used for the prices of coal, natural gas and oil. Equipment, machinery and road data are calculated for produced capital. In this research, we utilized GDP as an output. All capital wealth in this calculation is in millions, constant 2005 US dollars.

4.1. Total factor productivity

Based on the estimating procedure explained in Section 3, we estimated each country's TFP, efficiency change and technological change for the 21 years included in the dataset. The means of each country's TFP change, efficiency change and technological change from 1990 to 2010 are presented in Figure 1 and Table 1.

Fig. 1. Average of total factor productivity (TFP) for 140 countries (1990–2010).

Table 1. Ranking and summary of estimated total factor productivity (TFP).

Table 1 and Figure 1 show the TFP changes for the 140 countries from 1990 to 2010. The countries in Table 1 are presented in descending order based on the magnitude of TFP changes. Table 1 shows Singapore and China as the two countries with the highest TFP growth. Singapore shows a 10.0% average growth in TFP (caused by steady growth in efficiency) and a 10.0% growth in technological change. The high TFP growth of Singapore has contributed to its rapid economic development. According to Han (Reference Han2017), the rapid economic development of Singapore can be attributed to its technocratic strategy and its environmental policy, which have led to its international reputation as a model green city due to its remarkable expansion of green spaces and infrastructure. Australia, the UK, India and Japan demonstrated TFP growth rates of 0.5%, 3.2%, 0.8% and 0.5%, respectively. The unweighted average growth in TFP across the 140 countries was 0.7%.

Figure 2 shows the annual mean TFP change, technological change and efficiency change over the entire study period (1990–2010) for the 140 countries. On average, TFP values increased in many countries throughout the period of study. The worst TFP change during the study period was from 2008 to 2009 and is attributable to the global financial crisis. The greatest technological and efficiency changes were in 1992–1993 and 2002–2003, respectively.

Fig. 2. Mean total factor productivity (TFP) change, efficiency change and technological change (1990–2010).

Table 2 shows the mean TFP change, efficiency change and technological change results based on the different regions from 1990 to 2010. It is clear that Asia demonstrated the greatest TFP growth (1.0%), followed by Latin America and the Caribbean (0.9%). North America showed the lowest (and decreasing) TFP, followed by Europe (0.1%).

Table 2. Means of total factor productivity (TFP), efficiency change and technological change (1990–2010) based on regions.

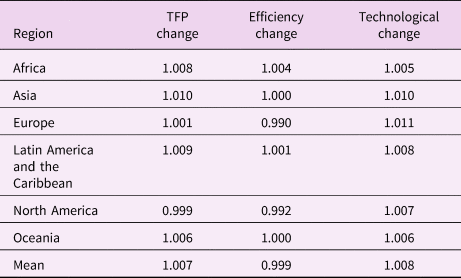
Figure 3 shows the cumulative TFP indices from 1990 to 2010 based on six regions. Asia clearly experienced the greatest cumulative growth, especially in 2010, followed by Africa, Latin America and the Caribbean. North America and Oceania were at the bottom, whereas Asia still experienced the greatest cumulative growth compared to global growth in TFP. According to Clémençon (Reference Clémençon1997), economic integration and free trade might have been the factors that further boosted the economic growth of Asian countries, especially in the Association of Southeast Asian Nations (ASEAN). Sonnenfeld and Mol (Reference Sonnenfeld and Mol2006) argued that the Asia-Pacific region is unquestionably one of the most economically dynamic areas in the world. For instance, countries such as China, India, Malaysia, Vietnam and Thailand demonstrated steady economic growth over the two decades, even while facing the financial crisis of the late 1990s.

Fig. 3. Mean total factor productivity (TFP) change in six regions (1990–2010).

4.2. IW-TFP Adjusted

Using the results of the new TFP and based on the method described in Section 3, we estimated each country's IW-TFP Adjusted for 1990–2010. In this study, we used each annual per capita IW and estimated the percentage change in TFP on the IW as an indicator of sustainable development. We calculated the growth rate of per capita IW in order to estimate the IW-TFP Adjusted. We followed the same process as in Arrow et al. (Reference Arrow, Dasgupta, Goulder, Daily, Ehrlich, Heal and Walker2004) through the use of TFP growth from Collins and Bosworth (Reference Collins and Bosworth1996), which is based on GDP output. The results for the IW-TFP Adjusted are shown in Table 3.

Table 3. Result of inclusive wealth with total factor productivity adjusted (IW-TFP Adjusted) per capita and percentage of change.

Table 3 shows the post-IW-TFP adjustment figures for the 140 countries over 21 years from 1990 to 2010. Table 3 demonstrates that among those 140 countries, 100 countries, representing 71% of nations, showed a positive IW-TFP Adjusted. Before adjustment, 85 countries demonstrated positive IW; after modification, 25 countries moved from the negative to the positive bracket, and only 10 nations experienced the reverse. Belize, Benin, Botswana, Cambodia, Colombia, Côte d'Ivoire, Ecuador, Ghana, Guyana, Indonesia, Iran, Malawi, Mali, Mozambique, Namibia, Nepal, Nicaragua, Niger, Nigeria, Peru, the Syrian Arab Republic, Tanzania, Trinidad and Tobago, Uganda and Yemen moved from negative to positive. Croatia, Gambia, Haiti, Jamaica, Kazakhstan, Kenya, Kyrgyzstan, the Russian Federation, Serbia and Ukraine moved from positive to negative. The movement of several countries from negative to positive positions proved that TFP can also be considered as one of the factors that has an impact on these results. Figures 4 and 5 show the percentages of growth rate (per capita) on IW before and after TFP adjustment.

Fig. 4. Percentage of growth rate (per capita) on inclusive wealth before IW-TFP Adjusted.

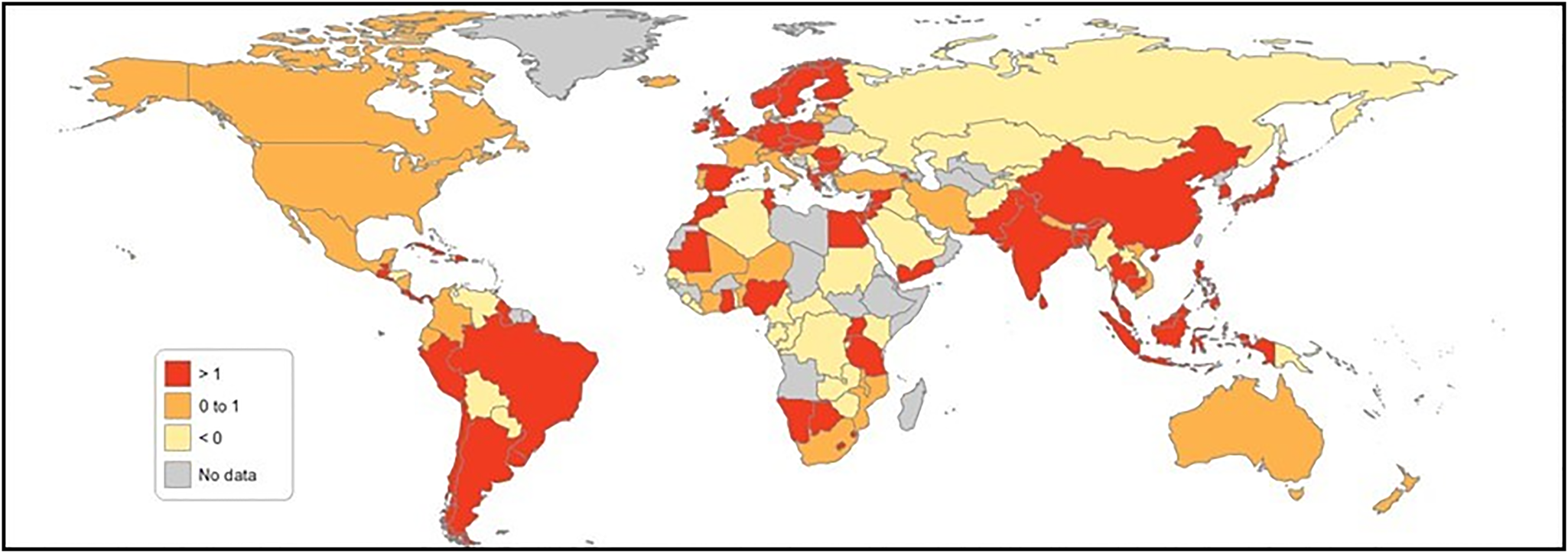
Fig. 5. Percentage of growth rate (per capita) on inclusive wealth after IW-TFP Adjusted.

4.3. IWI Adjusted

We also measured how countries’ performance was affected by three main factors (carbon damage, oil capital gains and TFP) that were taken into consideration for the adjustment. We refer to this new adjustment as IWI Adjusted and measure all of the countries in the sample on a per capita basis. We also calculated the annual average growth rate in wealth and population in order to estimate the change in wealth.

Before the new adjustment, 55 countries experienced negative growth per capita IW, representing almost 39% of the 140 countries in this study. A total of 85 out of the 140 countries showed a positive growth rate in wealth, representing almost 77% of the total sample. After adjusting three main factors (carbon damage, oil capital gains and the latest TFP results), the number of countries showing positive growth rates in wealth increased from 85 to 101. Twenty-seven countries moved from the negative to the positive bracket after the wealth adjustment. The following 11 countries moved from the positive to the negative bracket after all three factors were taken into consideration: Croatia, Gambia, Haiti, Jamaica, Kenya, Kyrgyzstan, Latvia, Portugal, the Russian Federation, Serbia and Ukraine. Of the 140 countries, 40 (almost 29%) remained in the negative bracket after the adjustment. These 40 countries were confronted by long-term issues related to sustaining their current consumption patterns.

Figures 6 and 7 show that the following 27 countries moved from the negative to the positive bracket after all three factors were adjusted: Algeria, Botswana, Cambodia, Colombia, Ecuador, Ghana, Guyana, Indonesia, Iran, Iraq, Kuwait, Malawi, Mali, Namibia, Nicaragua, Niger, Nigeria, Peru, Qatar, Saudi Arabia, Sudan, the Syrian Arab Republic, Trinidad and Tobago, Uganda, the United Republic of Tanzania, Venezuela and Yemen. Both Figures 6 and 7 show the percentages of growth rate (per capita) on IW before and after the three-component adjustment.

Fig. 6. Percentage of growth rate (per capita) on inclusive wealth before IWI Adjusted.

Fig. 7. Percentage of growth rate (per capita) on inclusive wealth after IWI Adjusted.

Among the three main factors, TFP had the largest contribution by moving 25 countries from the negative to the positive bracket after the energy depletion factor took oil capital gains into consideration. In the case of climate change, most of the countries in this study experienced a negative impact. Thus, TFP can be considered as one of the factors that significantly contributes to several countries’ movement from the negative to the positive bracket. Table 4 shows the results of TFP Adjusted per capita after three main factors were taken into consideration (as explained in Section 3.3) and its percentage change.

Table 4. Results after total factor productivity adjusted (TFP Adjusted) per capita and percentage of change.

4.4. G7 countries

In this study, we also learned something about the major development economies of the G7 countries. There are seven countries in the G7: Canada, Japan, France, Germany, Italy, the UK and the USA. Figure 8 shows the wealth composition of the G7 countries from 1990 to 2010. Most of the G7 countries have human capital advantages that can be considered as major contributors to their TFP and economic growth. In the case of Canada, its natural capital represents the second-highest wealth contribution after human capital, representing 31% of Canada's IW. The UK's growth in productivity contributes more than its human capital. This success can be attributed to tougher competition in the product and labour markets, an increase in higher education and the faster adoption of information, communication and innovation policies (Aghion et al., Reference Aghion, Beesley, Browne, Caselli, Lambert, Lomax and van Reenen2013).

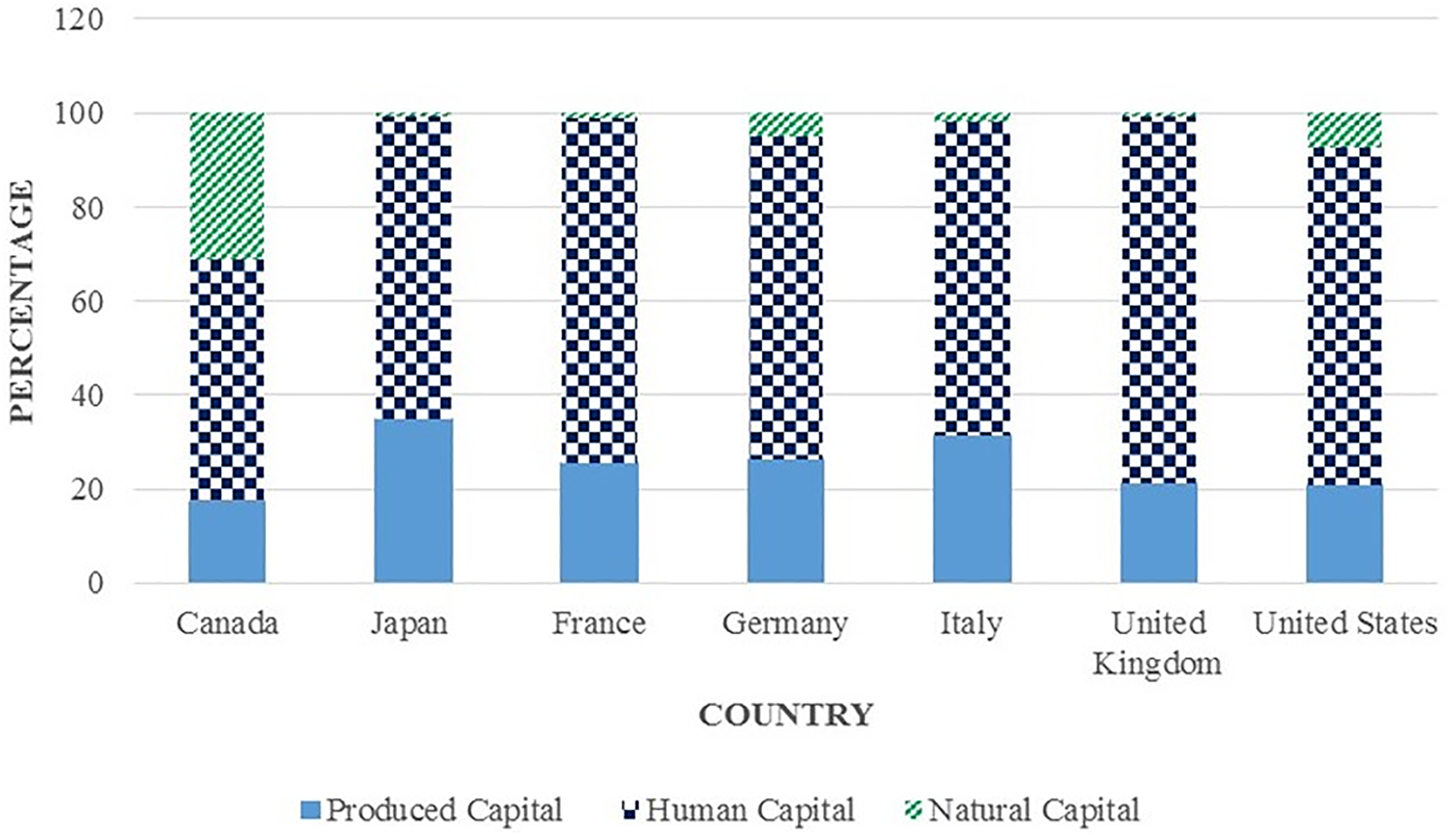
Fig. 8. Percentage of wealth composition of the G7 countries (1990–2010).

The combination of human and produced capital in Japan has supported its growth and efficiency increase in other components throughout the study period. This is due to the fact that labour productivity in Japan after 1995 has been attributed to a compositional shift in the labour market to increase the amount of higher-quality labour due to a greater demand for higher education (Chun et al., Reference Chun, Tsutomu, Pyo and Konomi2015). The UK has the highest amount of human capital in the G7 at 78% of total wealth, followed by France at 73%. Therefore, human capital is the foremost contributor to the IW growth rates for all of the G7 countries. On average, human capital contributed to 68% of overall IW, whereas produced capital contributed to 25% and natural capital contributed to 7% if we look at all of the G7 countries as a single group.

The TFP growth of the G7 countries has undergone a powerful revival since 1990, as is depicted in Figure 9. The TFP growth rate, which considers natural capital as an input, shows that the UK's TFP growth rate pattern has increased. The UK's TFP growth based on IW in 1990–1991 occur as rapidly as France and Germany, but its progress continued from 1992 to 2010. Although France and Germany started the 20-year period ahead of the UK, the UK finished ahead by 2010. The trend in TFP growth among the G7 countries since the mid-1990s has attracted significant attention because labour productivity growth represents an important factor in economic growth stability (Jablanovic, Reference Jablanovic2012).

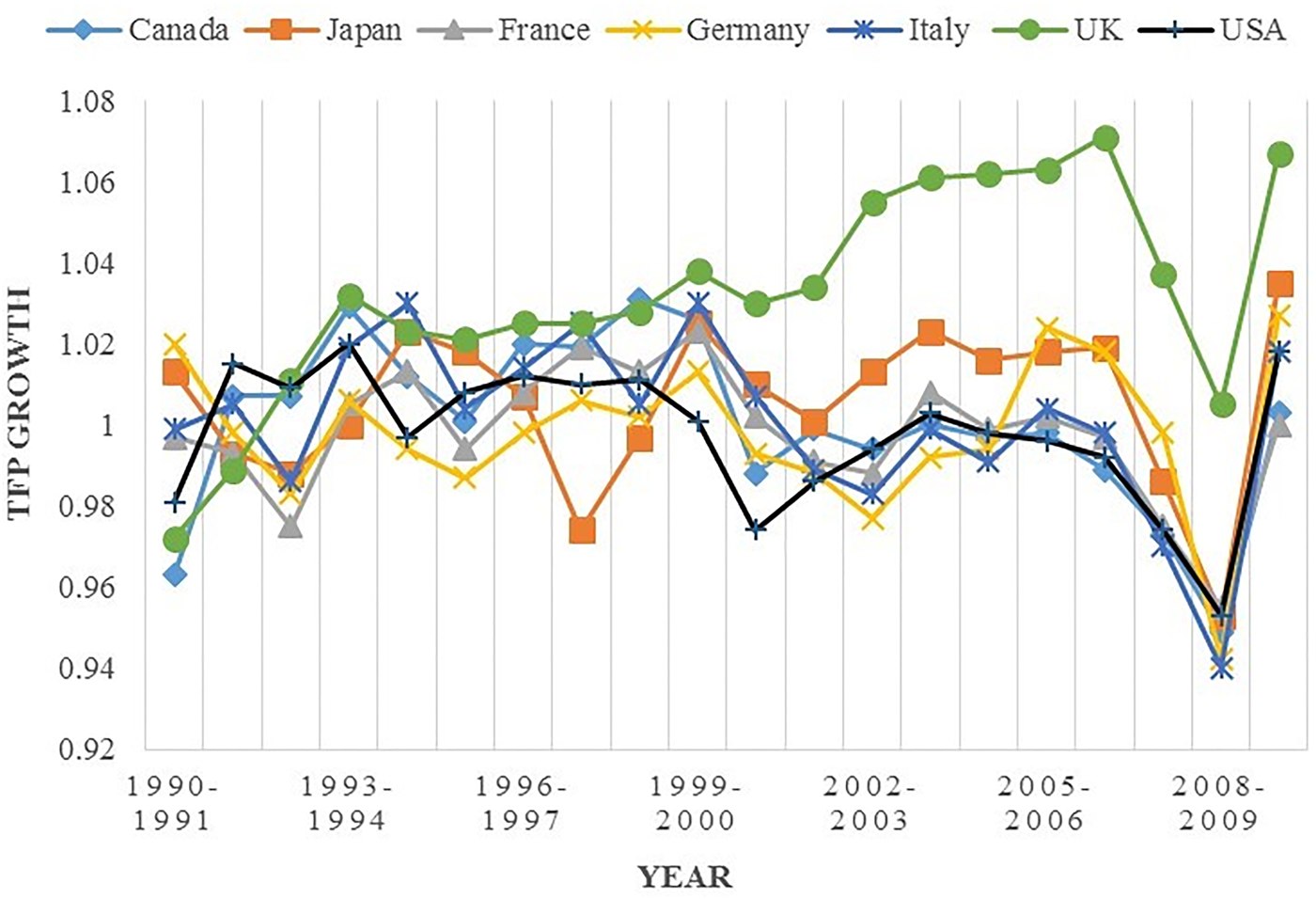
Fig. 9. Total factor productivity (TFP) growth of the G7 countries (1990–2010).

The UK's TFP growth exceeded that of the USA from 1992. Although the entire G7 suffered during the financial crisis of 2008–2009, the UK continued to enjoy the greatest TFP growth in the G7. From 2005 to 2010, TFP growth for most of the G7 countries was slowed considerably by the global financial and economic crisis of 2008–2009. Recovery from the Great Recession of 2007–2009 by the USA, Japan, Canada and the four European economies of the G7 has been slow and irregular (Jorgenson & Khuong, Reference Jorgenson and Vu2013). The Asian currency and financial crises of 1997 and 1998 affected Japan's TFP growth more than that of the other G7 countries because Japan is the only Asian country in the G7. Japan recovered from the Asian financial crisis, and in 1999, Japan's TFP growth was greater than that of France, Germany and the USA. Japan's TFP growth was revived from 2000 to 2010, and Italy showed the weakest performance during the global crisis.