Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-06T02:02:49.870Z Has data issue: false hasContentIssue false
  • English
  • Français

Wilson spaces and stable splittings of BTr

Published online by Cambridge University Press:  18 May 2009

C. A. McGibbon
C. A. McGibbon
Affiliation:
Mathematics Department, Wayne State University, Detroit, Michigan, 48202, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Q(X) denote 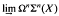and let BTr denote the classifying space of the r-torus. In [8], Segal showed that Q(BT1) is homotopy equivalent to a product BU × F where BU denotes the classifying space for stable complex vector bundles and F a space with finite homotopy groups. This result has been a very useful one. For example, in [5] it was used to show that up to a stable homotopy equivalence there is only one loop structure on the 3-sphere at each odd prime p. (The subsequent work of Dwyer, Miller, and Wilkerson shows this result is even true unstably, at every prime p.) In [6] it was used to classify, up to homology, the stable self maps of the projective spaces ℂPn and ℍPn. In [5] I asked if a splitting similar to Segal's might exist for Q(BTr) when r≥2. In particular, since the homotopy and homology groups of BU are torsion free it seemed natural to ask if Q(BTr), when r>, could likewise contain a retract with torsion free homology and homotopy groups and whose complement is rationally trivial. The purpose of this note is to show that the answer is no.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 3 , September 1994 , pp. 287 - 290
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Baker, A., Carlisle, D., Gray, B., Hilditch, S., Ray, N. and Wood, R., On the iterated complex transfer, Math. Z. 199, (1988), 191–207.CrossRefGoogle Scholar
2.Carlisle, D., Eccles, P., Hilditch, S., Ray, N., Schwartz, L., Walker, G. and Wood, R., Modular representations of GL(n, p), splitting of , and the β-family as framed hypersurfaces, Math. Z. 189 (1985), 239–261.CrossRefGoogle Scholar
3.Carlisle, D. and Walker, G., Poincaré series for the occurrence of certain modular representations of GL(n, p) in the symmetric algebra, Proc. Royal Soc. Edinburgh, 113A (1989), 27–41.CrossRefGoogle Scholar
4.Dwyer, W. G., Miller, H. R. and Wilkerson, C. W., Homotopical uniqueness of BS 3, Lecture Notes in Math. 1298 (Springer 1987), 90–105.Google Scholar
5.McGibbon, C. A., Stable properties of rank 1 loop spaces, Topology 20 (1981), 109–118,CrossRefGoogle Scholar
6.McGibbon, C. A., Self maps of projective spaces, Trans. Amer. Math. Soc. 271 (1982), 325–346.Google Scholar
7.Peterson, F. P., The mod p homotopy type of BSO and F/PL, Bol. Soc. Math. Mexicana 14 (1969), 22–28.Google Scholar
8.Segal, G. B., The stable homotopy of complex projective space, Quart. J. Math. Oxford 24 (2), (1973), 1–5.CrossRefGoogle Scholar
9.Wilson, W. S., The Ω-spectrum for Brown-Peterson cohomology, part II, Amer. J. Math. 97 (1975), 101–123.CrossRefGoogle Scholar
10.Zabrodsky, A., Hopf spaces (North Holland, 1976).Google Scholar