Hostname: page-component-55f67697df-sqlfs Total loading time: 0 Render date: 2025-05-11T00:50:27.492Z Has data issue: false hasContentIssue false
  • English
  • Français

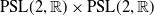Weyl chamber length compactification of the $\textrm{PSL}(2,{\mathbb{R}})\times \textrm{PSL}(2,{\mathbb{R}})$ maximal character variety

Part of: Lie groups Structure and classification of infinite or finite groups Deformations of analytic structures Special aspects of infinite or finite groups

Published online by Cambridge University Press:  27 September 2024

Marc Burger ,
Alessandra Iozzi ,
Anne Parreau  and
Maria Beatrice Pozzetti
Marc Burger
Affiliation:
Department Mathematik, ETH Zentrum, Zürich, CH-8092, Switzerland
Alessandra Iozzi
Affiliation:
Department Mathematik, ETH Zentrum, Zürich, CH-8092, Switzerland
Anne Parreau*
Affiliation:
Univ. Grenoble Alpes, CNRS, IF, Grenoble, 38058, France
Maria Beatrice Pozzetti
Affiliation:
Institute for Mathematics, Heidelberg University, Heidelberg, 69120, Germany
*
Corresponding author: A. Parreau; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the vectorial length compactification of the space of conjugacy classes of maximal representations of the fundamental group $\Gamma$ of a closed hyperbolic surface 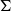$\Sigma$ in 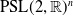$\textrm{PSL}(2,{\mathbb{R}})^n$. We identify the boundary with the sphere ${\mathbb{P}}(({\mathcal{ML}})^n)$, where 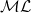$\mathcal{ML}$ is the space of measured geodesic laminations on 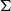$\Sigma$. In the case 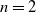$n=2$, we give a geometric interpretation of the boundary as the space of homothety classes of 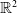${\mathbb{R}}^2$-mixed structures on 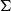$\Sigma$. We associate to such a structure a dual tree-graded space endowed with an 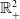${\mathbb{R}}_+^2$-valued metric, which we show to be universal with respect to actions on products of two 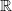$\mathbb{R}$-trees with the given length spectrum.

Keywords

compactifications of character varietiessurface groupsmaximal representationsproducts of trees

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups
Secondary: 32G15: Moduli of Riemann surfaces, Teichmüller theory 20E08: Groups acting on trees 20F69: Asymptotic properties of groups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 67 , Issue 1 , January 2025 , pp. 11 - 33
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bestvina, M., Degenerations of the hyperbolic space, Duke Math. J. 56(1) (1988), 143–161.CrossRefGoogle Scholar
Bonahon, F., The geometry of Teichmüller space via geodesic currents, Invent. Math. 92(1) (1988), 139–162.CrossRefGoogle Scholar
Burger, M., Iozzi, A., Labourie, F. and Wienhard, A., Maximal representations of surface groups: symplectic Anosov structures, Pure Appl. Math. Q. 1(3, Special Issue: In memory of Armand Borel. Part 2) (2005), 543–590.CrossRefGoogle Scholar
Burger, M., Iozzi, A., Parreau, A. and Pozzetti, M. B., Currents, systoles, and compactifications of character varieties, Proc. Lond. Math. Soc. (3) 123 (2021), 565–596.CrossRefGoogle Scholar
Burger, M., Iozzi, A., Parreau, A. and Pozzetti, M. B., Positive crossratios, barycenters, trees and applications to maximal representations, Groups Geom. Dyn. (2024). https://doi.org/10.48550/arXiv.2103.17161Google Scholar
Burger, M., Iozzi, A. and Wienhard, A., Surface group representations with maximal Toledo invariant, Ann. Math. 172(1) (2010), 517–566.CrossRefGoogle Scholar
Culler, M. and Morgan, J. W., Group actions on $\mathbb R$ -trees, Proc. Lond. Math. Soc. (3) 55 (1987), 571–604.CrossRefGoogle Scholar
Druţu, C. and Sapir, M., Tree-graded spaces and asymptotic cones of groups. (With an appendix by Denis Osin and Mark Sapir), Topology 44(5) (2005), 959–1058.CrossRefGoogle Scholar
Duchin, M., Leininger, C. J. and Rafi, K., Length spectra and degeneration of flat metrics, Invent. Math. 182(2) (2010), 231–277.CrossRefGoogle Scholar
Fathi, A., Laudenbach, F. and Poénaru, V., Thurston’s work on surfaces, vol. 48 (Princeton University Press, 2012).CrossRefGoogle Scholar
Gardiner, F. P. and Masur, H., Extremal length geometry of Teichmüller space, Complex Var. Theory Appl. 16(2-3) (1991), 209–237.Google Scholar
Gardiner, F. P. and Wang, Z., Extremal annuli on the sphere, in Quasiconformal Mappings, Riemann Surfaces, and Teichmuller Spaces: AMS Special Session in Honor of Clifford J. Earle, October 2-3, 2010, Syracuse University, Syracuse, New York, vol. 575 (2012), 89.CrossRefGoogle Scholar
Guirardel, V., Cœur et nombre d’intersection pour les actions de groupes sur les arbres, Ann. Sci. École Norm. Sup. (4) 38(6) (2005), 847–888.CrossRefGoogle Scholar
Kapovich, M., Hyperbolic manifolds and discrete groups (Birkhäuser, Boston, MA, 2001). Reprint of the 2001 hardback edition, 2009.Google Scholar
Martelli, B., An introduction to geometric topology (CreateSpace Independent Publishing Platform, 2016).Google Scholar
Martone, G., Ouyang, C. and Tamburelli, A., A closed ball compactification of a maximal component via cores of trees (2021). arXiv e-prints, page arXiv:2110.06106.Google Scholar
Morgan, J. W. and Shalen, P. B., Valuations, trees, and degenerations of hyperbolic structures. I, Ann. Math. 120(3) (1984), 401–476.CrossRefGoogle Scholar
Morzadec, T., Geometric compactification of moduli spaces of half-translation structures on surfaces, Geom. Dedicata 193(1) (2018), 31–72.CrossRefGoogle Scholar
Ouyang, C., High energy harmonic maps and degeneration of minimal surfaces, Geom. Topol. 27 (2023), 1691–1746.CrossRefGoogle Scholar
Ouyang, C. and Tamburelli, A., Limits of Blaschke metrics, Duke Math. J. 170(8) (2021), 1683–1722.CrossRefGoogle Scholar
Ouyang, C. and Tamburelli, A., Length spectrum compactification of the $\textrm{SO}_{0}(2,3)$ -Hitchin component, Adv. Math. 420, Article ID 108997 (2023).CrossRefGoogle Scholar
Ouyang, C. and Tamburelli, A., Boundary of the Gothen components, Topol. Appl. 326, (2023). Article ID 108420.CrossRefGoogle Scholar
Parreau, A., La distance vectorielle dans les espaces symmetriques et les immeubles affines. In preparation.Google Scholar
Parreau, A., Espaces de représentations complètement réductibles, J. Lond. Math. Soc. 83(3) (2011), 545–562.CrossRefGoogle Scholar
Parreau, A., Compactification d’espaces de représentations de groupes de type fini, Math. Z. 272(1-2) (2012), 51–86.CrossRefGoogle Scholar
Parreau, A., Invariant subspaces for some surface groups acting on A2-Euclidean buildings, Trans. Am. Math. Soc. 375(04) (2022), 2293–2339.CrossRefGoogle Scholar
Paulin, F., Topologie de Gromov équivariante, structures hyperboliques et arbres réels, Invent. Math. 94(1) (1988), 53–80.CrossRefGoogle Scholar